Question

Let f(x) = max {$x^2, (1-x)^2, 2x(1-x)$}, where $0\le x\le1$.
Determine the area of the region bounded by the curves
y=f (x), X-axis, x = 0 and x = 1.

Answer 1

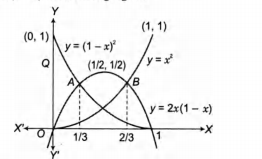
We can draw the graph of $y=x^2$, $y=(1-x)^2$ and
y = 2 x (1 - x) in following figure
Now, to get the point of intersection of $y=x^2$ and y = 2x (1 - x), we get,
$x^2=2x(1-x) \Rightarrow 3x^2=2x$
$\Rightarrow $ x(3x-2)=0 $\Rightarrow $ x = 0, $\frac {2}{3}$
Similarly, we can find the coordinate of the points of
intersection of
$y=(1-x^2)$ and y = 2x (1 - x) are $x=\frac {1}{3}$ and x=1
From the figure, it is clear that,
$\Bigg \{ \begin{array} \ (1 - x)^2, \\ 2x ( 1 - x), \\ x^2, \\ \end{array} \begin{array} \ if 0 \le x \le \frac {1}{3} \\ if \frac {1}{3} \le x \le \frac {2}{3} \\ if \frac {2}{3} \le x \le 1 \\ \end{array}$
$\therefore $ The required area
$A=\int\limits_0^1 f(x) dx$
$=\int\limits_0^{\frac{1}{3}} (1-x)^2 dx+\int\limits_{\frac{1}{3}}^{\frac{2}{3}} 2x(1-x) dx+\int\limits_{\frac{2}{3}}^{1} x^2 dx$
$=\Big[ -\frac {1}{3}(1-x)^3\Big]_0^\frac {1}{3}+\Big[ x^2-\frac {2x^3}{3}\Big]_{\frac {1}{3}}^{\frac {2}{3}}$ +$\Big[ \frac {1}{3}x^3\Big]_{\frac {2}{3}}^ {1}$
=$\Big[ -\frac {1}{3}\Big( \frac {2}{3}\Big)^3+\frac {1}{3}\Big]$+$\Big[ \Big( \frac {2}{3}\Big)^3+\frac {2}{3} \Big(\frac {2}{3}\Big)^{3}-\Big(\frac {1}{3}\Big)^{2}+\frac {2}{3} \Big(\frac {1}{3}\Big)^{3}\Big]$+$\Big[ {\frac {1}{3}}(1)-\frac {1}{3}\Big( \frac {2}{3}\Big)^3\Big]$
$=\frac {19}{81}+\frac {13}{81}+\frac {19}{81}=\frac {17}{27}$ sq unit