JEE Main Question Paper with Solution 2023 January 24th Shift 1 - Morning

JEE Main Physics Question Paper with Solution 2023 January 24th Shift 1 - Morning

Q1. Given below are two statements : one is labelled as Assertion $A$ and the other is labelled as Reason $R$
Assertion A: Photodiodes are preferably operated in reverse bias condition for light intensity measurement.
Reason R : The current in the forward bias is more than the current in the reverse bias for a $p-n$ junction diode.
In the light of the above statements, choose the correct answer from the options given below:

A

A is true but $R$ is false

B

Both $A$ and $R$ are true and $R$ is the correct explanation of $A$

C

A is false but $R$ is true

D

Both $A$ and $R$ are true but $R$ is $N O T$ the correct explanation of $A$

Solution

Photodiodes are operated in reverse bias as fractional change in current due to light is more easy to detect in reverse bias.

Q2. A travelling wave is described by the equation
$y(x, t)=[0.05 \sin (8 x-4 t)] m$
The velocity of the wave is : [all the quantities are in SI unit]

A

$4 \,ms ^{-1}$

B

$8 \,ms ^{-1}$

C

$0.5 \, ms ^{-1}$

D

$2 \,ms ^{-1}$

Solution

From the given equation $k =8 \,m ^{-1}$
and $\omega=4 \,rad / s$ Velocity of wave $=\frac{\omega}{ k }$
$v =\frac{4}{8}=0.5\, m / s$

Q3. Two long straight wires $P$ and $Q$ carrying equal current $10\, A$ ench were kept parallel to each other at $5 \, cm$ distance. Magnitude of magnetic force experienced by $10 \, cm$ length of wire $P$ is $F_1$ If distance between wires is halved and currents on them are doubled, force $F_2$ on $10 \, cm$ length of wire $P$ will be:

A

$10 F _1$

B

$8 F _1$

C

$\frac{F_1}{8}$

D

$\frac{F_1}{10}$

Solution

Force per unit length between two parallel straight
$ \text { wires }=\frac{\mu_0 i_1 i_2}{2 \pi d} $
$ \frac{F_1}{F_2}=\frac{\frac{\mu_0(10)^2}{2 \pi(5 cm )}}{\frac{\mu_0(20)^2}{2 \pi\left(\frac{5 cm }{2}\right)}}=\frac{1}{8}$
$ \Rightarrow F_2=8 F_1$

Q4. Consider the following radioactive decay process
${ }_{84}^{218} A \xrightarrow{\alpha} A_1 \xrightarrow{\beta^{-}}A_2 \xrightarrow{\gamma} A_3 \xrightarrow{\alpha} A_4 \xrightarrow{\beta^{+}} A_5 \xrightarrow{\gamma}A_6$
The mass number and the atomic number of $A_6$ are given by:

A

211 and 80

B

210 and 80

C

210 and 82

D

210 and 84

Solution

$ { }_{84}^{218} A \stackrel{\alpha}{\longrightarrow}{ }_{82}^{214} A _1 \stackrel{\beta^{-}}{\longrightarrow}{ }_{83}^{214} A _2 \stackrel{\gamma}{\longrightarrow}{ }_{83}^{214} A _3 $
${ }_{83}^{214} A _3 \stackrel{\alpha}{\longrightarrow}{ }_{81}^{210} A _4 \stackrel{\beta^{+}}{\longrightarrow}{ }_{80}^{210} A _5 \stackrel{\gamma}{\longrightarrow}{ }_{80}^{210} A _6$

Q5. From the photoelectric effect experiment, following observations are made. Identify which of these are correct.
A. The stopping potential depends only on the work function of the metal.
B. The saturation current increases as the intensity of incident light increases.
C. The maximum kinetic energy of a photo electron depends on the intensity of the incident light.
D. Photoelectric effect can be explained using wave theory of light.
Choose the correct answer from the options given below:

A

A, B, D only

B

B only

C

A, C, D only

D

B, C only

Solution

(A) Stopping potential depends on both frequency of light and work function.
(B) Saturation current  intensity of light
(C) Maximum KE depends on frequency
(D) Photoelectric effect is explained using particle theory

Q6. $1 \,g$ of a liquid is converted to vapour at $3 \times 10^5 Pa$ pressure. If $10 \%$ of the heat supplied is used for increasing the volume by $1600 \, cm ^3$ during this phase change, then the increase in internal energy in the process will be:

A

$4800 \, J$

B

$4320 \, J$

C

$4.32 \times 10^8 \, J$

D

$432000 \, J$

Solution

Work done $= P \Delta V$
$=3 \times 10^5 \times 1600 \times 10^{-6}$
$=480 J$
Only $10 \%$ of heat is used in work done.
Hence $\Delta Q=4800 J$
The rest goes in internal energy, which is $90 \%$ of heat.
Change in internal energy $=0.9 \times 4800=4320 J$

Q7. A modulating signal is a square wave, as shown in the figure.
image
If the carrier wave is given as $c ( t )=2 \sin (8 \pi t)$ volts, the modulation index is:

A

$\frac{1}{3}$

B

1

C

$\frac{1}{2}$

D

$\frac{1}{4}$

Solution

Modulation index
$ =\frac{\text { Amplitude of mod ulating signal }}{\text { Amplitude of carrier wave }} $
$ \mu=\frac{1}{2}$

Q8. Given below are two statements :
Statement I : The temperature of a gas is $-73^{\circ} C$. When the gas is heated to $527^{\circ} C$, the root mean square speed of the molecules is doubled.
Statement II : The product of pressure and volume of an ideal gas will be equal to translational kinetic energy of the molecules.
In the light of the above statements, choose the correct answer from the options given below:

A

Statement I is false but Statement II is true

B

Both Statement I and Statement II are true

C

Both Statement I and Statement II are false

D

Statement I is true but Statement II is false

Solution

Statement-I
$ T _1=-73^{\circ} C =200 K$
$T _2=527^{\circ} C =800 K$
$ \frac{ V _1}{ V _2}=\frac{\sqrt{\frac{3 RT _1}{ M }}}{\sqrt{\frac{3 RT _2}{ M }}}=\sqrt{\frac{ T _1}{ T _2}} $
$ =\sqrt{\frac{200}{800}}=\frac{1}{2}$
$V _2=2 V _1 \text { (True) }$
Statement-II
$PV = nRT$
Translational $KE =\frac{3}{2} nRT$ (False)

Q9. In $\vec{E}$ and $\vec{K}$ represent electric field and propagation vectors of the EM waves in vacuum, then magnetic field vector is given by: $(\omega-$ angular frequency):

A

$\frac{1}{\omega}(\bar{K} \times \bar{E})$

B

$\omega(\overline{ K } \times \overline{ E })$

C

$\bar{K} \times \bar{E}$

D

$\omega(\overline{ E } \times \overline{ K })$

Solution

Magnetic field vector will be in the direction of $\hat{ K } \times \hat{ E }$
magnitude of $B =\frac{ E }{ C }=\frac{ K }{\omega} E$
Or $\overrightarrow{ B }=\frac{1}{\omega}(\overrightarrow{ K } \times \overrightarrow{ E })$

Q10. A circular loop of radius $r$ is carrying current $I A$. The ratio of magnetic field at the center of circular loop and at a distance $r$ from the center of the loop on its axis is:

A

$1: 3 \sqrt{2}$

B

$2 \sqrt{2}: 1$

C

$3 \sqrt{2}: 2$

D

$1: \sqrt{2}$

Solution

Magnetic field due to current carrying circular loop on its axis is given as
$\frac{\mu_0 ir ^2}{2\left( r ^2+ x ^2\right)^{3 / 2}}$
At centre, $x=0, B_1=\frac{\mu_0 i}{2 r}$
At $x=r, B_2=\frac{\mu_0 i }{2 \times 2 \sqrt{2} r }$
$\frac{ B _1}{ B _2}=2 \sqrt{2}$

Q11. A $100\, m$ long wire having cross-sectional area $6.25 \times 10^{-4} \, m ^2$ and Young's modulus is $10^{10} Nm ^{-2}$ is subjected to a load of $250 \, N$, then the elongation in the wire will be:

A

$6.25 \times 10^{-3} m$

B

$4 \times 10^{-3} m$

C

$4 \times 10^{-4} m$

D

$6.25 \times 10^{-6} m$

Solution

Elongation in wire $\delta=\frac{ F \ell}{ AY }$
$ \delta=\frac{250 \times 100}{6.25 \times 10^{-4} \times 10^{10}} $
$ \delta=4 \times 10^{-3} m$

Q12. As per given figure, a weightless pulley $P$ is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if $g =10 \,/ s ^2$ )

A

$(4 \sqrt{3}-1) N$

B

$4(\sqrt{3}-1) N$

C

$(4 \sqrt{3}+1) N$

D

$4(\sqrt{3}+1) N$

Solution

image
Solving (1) and (2) we get.
$ 20 \sqrt{3}-T=4 T -20$
$ T =4(\sqrt{3}+1) N$

Q13. As shown in the figure, a network of resistors is connected to a battery of $24 V$ with an internal resistance of $3 \Omega$. The currents through the resistors $R_4$ and $R_5$ are $I_4$ and $I_5$ respectively. The values of $I _4$ and $I _5$ are: $(24 V , 3 \Omega)$

A

$I _4=\frac{8}{5} A$ and $I _5=\frac{2}{5} A$

B

$I _4=\frac{6}{5} A$ and $I _5=\frac{24}{5} A$

C

$I _4=\frac{2}{5} A$ and $I _5=\frac{8}{5} A$

D

$I _4=\frac{24}{5} A$ and $I _5=\frac{6}{5} A$

Solution

Equivalent resistance of circuit
$R _{ eq } =3+1+2+4+2$
$ =12 \Omega$
Current through battery $i =\frac{24}{12}=2 A$
$ I _4=\frac{ R _5}{ R _4+ R _5} \times 2=\frac{5}{20+5} \times 2=\frac{2}{5} A $
$ I _5=2-\frac{2}{5}=\frac{8}{5} A$

Q14. Choose the correct answer from the options given below:
LIST I LIST II
A Planck's constant (h) 1 $\left[ M ^1 L ^2 T ^{-2}\right]$
B Stopping potential (Vs) 2 $\left[ M ^1 L ^1 T ^{-1}\right]$
C Work function $(ø) $ 3 $\left[ M ^1 L ^2 T ^{-1}\right]$
D Momentum (p) 4 $\left[ M ^1 L ^2 T ^{-3} A ^{-1}\right]$

A

A-II, B-IV, C-III, D-I

B

A-III, B-IV, C-I, D-II

C

A-I, B-III, C-IV, D-II

D

A-III, B-I, C-II, D-IV

Solution

(A) Planck's constant
$ h v= E $
$ h =\frac{ E }{v}=\frac{ M ^1 L ^2 T ^{-2}}{ T ^{-1}}= M ^1 L ^2 T ^{-1}$
(B) $E = qV$
$V=\frac{E}{q}=\frac{M^1 L^2 T^{-2}}{A^1 T^1}=M^1 L^2 T^{-3} A^{-1} \text { (IV) }$
(C) $\phi$ (work function $)=$ energy
$= M ^1 L ^2 T ^{-2}$...(I)
(D) Momentum (p) = F.t
$=M^1 L^1 T^{-2} T^1$...(II)
$=M^1 L^1 T^{-1}$

Q15. Given below are two statements :
Statement I: An elevator can go up or down with uniform speed when its weight is balanced with the tension of its cable.
Statement II: Force exerted by the floor of an elevator on the foot of a person standing on it is more than his/her weight when the elevator goes down with increasing speed.
In the light of the above statements, choose the correct answer from the options given below:

A

Statement I is false but Statement II is true

B

Statement I is true but Statement II is false

C

Both statement I and Statement II are false

D

Both Statement I and Statement II are true

Solution

Statement-1
When elevator is moving with uniform speed $T=F_g$
image
Statement-2
When elevator is going down with increasing speed, its acceleration is downward.
Hence

Q16. The weight of a body at the surface of earth is $18\, N$. The weight of the body at an altitude of $3200 \,km$ above the earth's surface is (given, radius of earth $R _{ e }=6400 \,km$ ):

A

19.6 N

B

9.8 N

C

4.9 N

D

8 N

Solution

Acceleration due to gravity at height $h$
$g ^{\prime}=\frac{ g }{\left[1+\frac{ h }{ R }\right]^2}$
So weight at given height
$mg ^{\prime}=\frac{ mg }{\left[1+\frac{ h }{ R }\right]^2}=\frac{18}{\left[1+\frac{1}{2}\right]^2}=8 N$

Q17. A conducting circular loop of radius $\frac{10}{\sqrt{\pi}} cm$ is placed perpendicular to a uniform magnetic field of $0.5 T$. The magnetic field is decreased to zero in $0.5 s$ at a steady rate. The induced emf in the circular loop at $0.25 s$ is:

A

$emf =1 mV$

B

$emf =100 mV$

C

$emf =5 mV$

D

$emf =10 mV$

Solution

$ EMF =\frac{ d \phi}{ dt }=\frac{ BA -0}{ t } $
$ A =\pi r ^2=\pi\left(\frac{0.1^2}{\pi}\right)=0.01$
$ B =0.5 $
$ EMF =\frac{(0.5)(0.01)}{0.5}=0.01 \,V =10 \,mV $

Q18. Given below are two statements :
Statement I : If the Brewster's angle for the light propagating from air to glass is $\theta_{ B }$, then the Brewster's angle for the light propagating from glass to air is $\frac{\pi}{2}-\theta_m$
Statement II : The Brewster's angle for the light propagating from glass to air is $\tan ^{-1}\left(\mu_{ g }\right)$ where $\mu_{ g }$ is the refractive index of glass.
In the light of the above statements, choose the correct answer from the options given below:

A

Both Statement I and Statement II are true

B

Both Statement I and Statement II are false

C

Statement I is true but Statement II is false

D

Statement I is false but Statement II is true

Solution

image
$ \mu_{ a } \sin i _1=\mu_{ g } \sin \left(90- i _1\right)$
$ \tan i _1=\frac{\mu_{ g }}{\mu_{ a }}$
When going from glass to air
$\tan i _2=\frac{\mu_{ a }}{\mu_{ g }}=\cot i _1$
Hence
$i _2=\frac{\pi}{2}- i _1$

Q19. The maximum vertical height to which a man can throw a ball is $136 \,m$. The maximum horizontal distance upto which he can throw the same ball is:

A

$68\, m$

B

$136\, m$

C

$192\, m$

D

$272\, m$

Solution

$H _{\max }=\frac{ v ^2}{2 g }=136\, m $
$ R _{\max }=\frac{ v ^2}{ g }=2 H _{\max } $
$ =2(136) $
$ =272\, m$

Q20. If two charges $q _1$ and $q _2$ are separated with distance ' $d$ ' and placed in a medium of dielectric constant $K$. What will be the equivalent distance between charges in air for the same electrostatic force?

A

$k \sqrt{d}$

B

$1 \cdot 5 d \sqrt{k}$

C

$2 d \sqrt{k}$

D

$d \sqrt{k}$

Solution

$ F =\frac{1}{\left(4 \pi \varepsilon_0\right)} \frac{ q _1 q _2}{ kd ^2}(\text { in medium) } $
$ F _{\text {Air }}=\frac{1}{4 \pi \varepsilon_0} \frac{ q _1 q _2}{ d ^{\prime 2}} $
$ F = F _{ Air }$
$ \frac{ q _1 q _2}{4 \pi \varepsilon_0 kd ^2}=\frac{ q _1 q _2}{4 \pi \varepsilon_0 d ^{\prime^2}} $
$ d ^{\prime}= d \sqrt{ k }$

Q21. A hole is drilled in a metal sheet. At $27^{\circ} C$, the diameter of hole is $5 cm$. When the sheet is heated to $177^{\circ} C$, the change in the diameter of hole is $d \times 10^{-3} cm$. The value of $d$ will be ___ if coefficient of linear expansion of the metal is $1.6 \times 10^{-5} /{ }^{\circ} C$.

Answer: 12

Solution

$d _0$ at $27^{\circ} C \,\& \,d _1$ at $177^{\circ} C$
$ d _1= d _0(1+\alpha \Delta T )$
$d _1- d _0=5 \times 1.6 \times 10^{-5} \times 150 \,cm$
$ =12 \times 10^{-3} cm$

Q22. A spherical body of mass $2\, kg$ starting from rest acquires a kinetic energy of $10000\, J$ at the end of $5^{\text {th }}$ second. The force acted on the body is ___$N$.

Answer: 40

Solution

$ \frac{1}{2} \times 2 \times v^2=10000 $
$\Rightarrow v^2=10000$
$ \Rightarrow v =100\, m / s $
$ \Rightarrow v = at = a \times 5=100 $
$ \Rightarrow a =20\, m / s ^2 $
$ F = ma =2 \times 20=40 \,N $

Q23. A hollow cylindrical conductor has length of $3.14\, m$, while its inner and outer diameters are $4 \, mm$ and $8 \, mm$ respectively. The resistance of the conductor is $n \times 10^{-3} \Omega$. If the resistivity of the material is $2.4 \times 10^{-8} \Omega m$. The value of $n$ is ___

Answer: 2

Solution

$R =\rho \frac{\ell}{ A }$, the cross-sectional area is $\pi\left( b ^2- a ^2\right)$
$ R =\rho \frac{\ell}{\pi\left( b ^2- a ^2\right)}=\frac{2.4 \times 10^{-8} \times 3.14}{3.14 \times\left(4^2-2^2\right) \times 10^{-6}} $
$ =2 \times 10^{-3} \Omega$
$\rightarrow n =2$

Q24. Assume that protons and neutrons have equal masses. Mass of a mucleon is $1.6 \times 10^{-27} kg$ and radius of nucleus is $1.5 \times 10^{-15} A ^{1 / 3} m$. The approximate ratio of the nuclear density and water density is $n \times 10^{13}$. The value of $n$ is ___

Answer: 11

Solution

$ \text { density of nuclei }=\frac{\text { mass of nuclei }}{\text { volume of nuclei }} $
$ \rho=\frac{1.6 \times 10^{-27} A }{\frac{4}{3} \pi\left(1.5 \times 10^{-15}\right)^3 A }$
$=\frac{1.6 \times 10^{-27}}{14.14 \times 10^{-45}}=0.113 \times 10^{18}$
$\rho_{ w }=10^3$
$ \text { Hence } \frac{\rho}{\rho_{ w }}=11.31 \times 10^{13} $

Q25. Vectors $a \hat{i}+b \hat{j}+\hat{k}$ and $2 \hat{i}-3 \hat{j}+4 \hat{k}$ are perpendicular to each other when $3 a+2 b=7$, the ratio of $a$ to $b$ is $\frac{x}{2}$ The value of $x$ is __

Answer: 1

Solution

For two perpendicular vectors
$ (a \hat{i}+b \hat{j}+\hat{k}) \cdot(2 \hat{i}-3 \hat{j}+4 \hat{k})=0 $
$2 a-3 b+4=0$
On solving, $2 a-3 b=-4$
Also given
$3 a +2 b =7$
We get $a =1, b =2$
$ \frac{a}{b}=\frac{x}{2} \Rightarrow x=\frac{2 a}{b}=\frac{2 \times 1}{2}$
$\Rightarrow x=1$

Q26. As shown in the figure, a combination of a thin plano concave lens and a thin plano convex lens is used to image an object placed at infinity. The radius of curvature of both the lenses is $30 \,cm$ and refraction index of the material for both the lenses is $1.75$. Both the lenses are placed at distance of $40 \,cm$ from each other. Due to the combination, the image of the object is formed at distance $x=$__ $cm$, from concave lens.

Answer: 120

Solution

$ \frac{1}{ f _1}=(1.75-1)\left(-\frac{1}{30}\right)$
$\Rightarrow f _1=-40 \,cm $
$ \frac{1}{ f _2}=(1.75-1)\left(\frac{1}{30}\right) \Rightarrow f _2=40\, cm$
Image from $L_1$ will be virtual and on the left of $L_1$ at focal length $40 \, cm$. So the object for $L _2$ will be $80 cm$ from $L _2$ which is $2 f$. Final image is formed at $80\, cm$ from $L _2$ on the right.
So $x=120$

Q27. A stream of a positively charged particles having $\frac{q}{ m }=2 \times 10^{11} \frac{ C }{ kg }$ and velocity $\vec{v}_0=3 \times 10^7 \hat{i} m / s$ is deflected by an electric field $1.8 kV / m$. The electric field exists in a region of $10 cm$ along $x$ direction. Due to the electric field, the deflection of the charge particles in the $y$ direction is___ $mm$.

Answer: 2

Solution

image
$ a =\frac{ F }{ m }=\frac{ qE }{ m }=\left(2 \times 10^{11}\right)\left(1.8 \times 10^3\right) $
$ =3.6 \times 10^{14} m / s ^2 $
$ \text { Time to cross plates }=\frac{ d }{ v } $
$ t =\frac{0.10}{3 \times 10^7} $
$ y =\frac{1}{2} at ^2=\frac{1}{2}\left(3.6 \times 10^{14}\right)\left(\frac{0.01}{9 \times 10^{14}}\right) $
$=0.2 \times 0.01$
$ =0.002 \,m $
$=2 \,mm $

Q28. In the circuit shown in the figure, the ratio of the quality factor and the band width is__ s.

Answer: 10

Solution

$ \Delta \omega=\frac{ R }{ L }$
$ Q =\frac{\omega_0}{\Delta \omega}=\omega_0 \frac{ L }{ R }$
$\omega_0=\frac{1}{\sqrt{3 \times 27 \times 10^{-6}}}=\frac{1}{9 \times 10^{-3}} $
$ \frac{ Q }{\Delta \omega}=\frac{\omega_0 \frac{ R }{ R }}{\frac{ R }{ L }}=\omega_0 \frac{ L ^2}{ R ^2}=\sqrt{\frac{1}{ LC }} \frac{ L ^2}{ R ^2} $
$=\frac{1}{9 \times 10^{-3}} \times \frac{9}{100}=10\, s $

Q29. Solid sphere $A$ is rotating about an axis $PQ$. If the radius of the sphere is $5 cm$ then its radius of gyration about $PQ$ will be $\sqrt{x} cm$. The value of $x$ is __

Answer: 110

Solution

$ I _{ cm }=\frac{2}{5} MR ^2 $
$ I _{ PQ }= I _{ cm }+ md ^2$
$ I _{ PQ }=\frac{2}{5} mR ^2+ m (10 cm )^2$
For radius of gyration
$ I _{ PQ }= mk ^2$
$ k ^2=\frac{2}{5} R ^2+(10 cm )^2$
$ =\frac{2}{5}(5)^2+100$
$ =10+100=110 $
$ k =\sqrt{110} cm $
$ x =110$

Q30. image
A block of a mass $2\, kg$ is attached with two identical springs of spring constant $20\, N / m$ each. The block is placed on a frictionless surface and the ends of the springs are attached to rigid supports (see figure). When the mass is displaced from its equilibrium position, it executes a simple harmonic motion. The time period of oscillation is $\frac{\pi}{\sqrt{x}}$ in SI unit. The value of $x$ is

Answer: 5

Solution

$ F =-2 kx , a =-\frac{2 kx }{ m }, \omega=\sqrt{\frac{2 k }{ m }}=\sqrt{\frac{2 \times 20}{2}}$
$ =\sqrt{20} \,rad / s $
$ T =\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{20}}=\frac{\pi}{\sqrt{5}} $
$ x =5$

JEE Main Chemistry Question Paper with Solution 2023 January 24th Shift 1 - Morning

Q1. In the depression of freezing point experiment
A. Vapour pressure of the solution is less than that of pure solvent
B. Vapour pressure of the solution is more than that of pure solvent
C. Only solute molecules solidify at the freezing point
D. Only solvent molecules solidify at the freezing point
Choose the most appropriate answer from the options given below:

A

A only

B

$B$ and $C$ only

C

A and C only

D

A and D only

Solution

image
Vapour pressure (V.P.) of solvent is greater than vapour pressure (V.P.) of solution. Only solvent freezes.

Q2. Order of Covalent bond;
A. $KF > KI ; LiF > KF$
B. $KF < KI ; LiF > KF$
C. $SnCl _4> SnCl _2 ; CuCl > NaCl$
D. $LiF > KF ; CuCl < NaCl$
E. $KF < KI ; CuCl > NaCl$
Choose the correct answer from the options given below:

A

A, B only

B

B, C only

C

B, C, E only

D

C, E only

Solution

According to Fajan's Rule,
A. $KF > KI$ - False; $LiF > KF$ - True
B. $KF < KI$ - True; $LiF > KF$ - True
C. $SnCl _4> SnCl _2-$ True; $CuCl > NaCl$ - True
D. $LiF > KF$ - True; $CuCl < NaCl -$ False
E. $KF < KI -$ True; $CuCl > NaCl -$ True

Q3. Match List I with List II
LIST I LIST II
A Reverberatory furnace I Pig Iron
B Electrolytic cell II Aluminum
C Blast furnace III Silicon
D Zone Refining furnace IV Copper
Choose the correct answer from the options given below:

A

A-I, B-III, C-II, D-IV

B

A-III, B-IV, C-I, D-II

C

A-I, B-IV, C-II, D-III

D

A-IV, B-II, C-I, D-III

Solution

Reverberatory furnace: Used for roasting of Copper.
Electrolytic cell : For reactive metal : Al
Blast furnace : Hematite to Pig Iron
Zone Refining furnace: For semiconductors : Si

Q4. Which of the following is true about freons?

A

These are radicals of chlorine and chlorine monoxide

B

These are chlorofluorocarbon compounds

C

All radicals are called freons

D

These are chemicals causing skin cancer

Solution

Fact

Q5. Match List I with List II
LIST I LIST II
A Chlorophyll 1 $Na _2 CO _3$
B Soda ash 2 $CaSO _4$
C Dentistry, Ornamental work 3 $Mg ^{2+}$
D Used in white washing 4 $Ca ( OH )_2$
Choose the correct answer from the options given below:

A

A-III, B-I, C-II, D-IV

B

A-II, B-III, C-IV, D-I

C

A-III, B-IV, C-I, D-II

D

A-II, B-I, C-III, D-IV

Solution

Chlorophyll : $Mg ^{+2}$ complex
Soda ash : $Na _2 CO _3$
Dentistry, Ornamental work : $CaSO _4$
Used in white washing : $Ca ( OH )_2$

Q6. The magnetic moment of a transition metal compound has been calculated to be $3.87$ B.M. The metal ion is

A

$T_1^{2+}$

B

$Mn ^{2+}$

C

$V ^{2+}$

D

$Cr ^{2+}$

Solution

$ Cr ^{+2}:[ Ar ], 3 d ^4, 4 s ^0 n =4, \mu=\sqrt{4(4+2)}=\sqrt{24} $
$ =4.89\, BM $
$ Mn ^{+2}:[ Ar ], 3 d ^5, 4 s ^0 n =5, \mu=\sqrt{5(5+2)}=\sqrt{35} $
$ =5.91 \,BM $
$V ^{+2}:[ Ar ], 3 d ^3, 4 s ^0 n =3, \mu=\sqrt{3(3+2)}=\sqrt{15} $
$=3.87 \,BM $
$ Ti ^{+2}:[ Ar ], 3 d ^2, 4 s ^0 n =2, \mu=\sqrt{2(2+2)}=\sqrt{8} $
$ =2.82 \,BM $

Q7. Decreasing order of the hydrogen bonding in following forms of water is correctly represented by
A. Liquid water
B. Ice
C. Impure water
Choose the correct answer from the options given below:

A

$C >B >A$

B

$B > A >C$

C

$A=B >C$

D

$A >B> C$

Solution

Ice > Liquid water > Impure water
Due to impurity extent of H-Bonding decreases.

Q8. '$R$. formed in the following sequence of reactions is :

A

B

C

D

Q9. Compound $( X )$ undergoes following sequence of reactions to give the Lactone $( Y )$.

A

B

C

D

Q10. An ammoniacal metal salt solution gives a brilliant red precipitate on addition of dimethylglyoxime. The metal ion is:

A

$Co ^{2+}$

B

$Fe ^{2+}$

C

$Ni ^{2+}$

D

$Cu ^{2+}$

Solution

$ Ni ^{+2}+2 DMG \xrightarrow{ NH _3( aq )}\underset{\text{Rosy Red complex }}{\left[ Ni ( DMG )_2\right]} $

Q11. Reaction of $BeO$ with ammonia and hydrogen fluoride gives A which on thermal decomposition gives $BeF _2$ and $NH _4 F$. What is ' $A ^{\prime}$ ?

A

$\left( NH _4\right) BeF _3$

B

$H _3 NBeF _3$

C

$\left( NH _4\right) Be _2 F _5$

D

$\left( NH _4\right)_2 BeF _4$

Solution

$ BeO +2 NH _3+4 HF \rightarrow\left( NH _4\right)_2 BeF _4+ H _2 O $
$ \left( NH _4\right)_2 BeF _4 \stackrel{\Delta}{\longrightarrow} BeF _2+ NH _4 F $

Q12. Assertion A :Hydrolysis of an alkyl chloride is a slow reaction but in the presence of NaI, the rate of the hydrolysis increases.
Reason R : $I ^{-}$is a good nucleophile as well as a good leaving group.
In the light of the above statements, choose the correct answer from the options given below

A

A is false but $R$ is tive

B

A is true but $R$ is false

C

Both $A$ and $R$ are true but $R$ is $N O T$ the correct explanation of $A$

D

Both $A$ and $R$ are true and $R$ is the correct explanation of $A$

Solution

The rate of hydrolysis of alkyl chloride improves because of better Nucleophilicity of $I^-$

Q13. Given below are two statements:
Statement I : Noradrenaline is a neurotransmitter.
Statement II : Low level of noradrenaline is not the cause of depression in human. In the light of the above statements, choose the correct answer from the options given below

A

Statement I is incorrect but Statement II is correct

B

Both Statement I and Statement II are correct

C

Statement I is correct but Statement II is incorrect

D

Both Statement I and Statement II are incorrect

Solution

Fact

Q14. It is observed that characteristic $X$-ray spectra of elements show regularity. When frequency to the power " $n$ " i.e. $v^n$ of $X$-rays emitted is plotted against atomic number " $Z$ ", following graph is obtained.

A

2

B

3

C

1

D

$\frac{1}{2}$

Solution

According to Henry Moseley $\sqrt{v} \alpha z - b$
So $n =\frac{1}{2}$

Q15. Which of the Phosphorus oxoacid can create silver mirror from $AgNO _3$ solution?

A

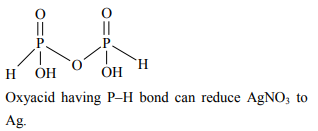
$H _4 P _2 O _7$

B

$\left( HPO _3\right)_n$

C

$H _4 P _2 O _6$

D

$H _4 P _2 O _5$

Q16. Increasing order of stability of the resonance structures is:
image
Choose the correct answer from the options given below:

A

$D , C , A , B$

B

C, D, A, B

C

D, C, B, A

D

$D , A , B$

Solution

No option is matching the correct answer. Order should be : C < A < B < D

Q17. In the following given reaction, ' $A$ ' is

A

B

C

D

Q18. The primary and secondary valencies of cobalt respectively in $\left[ Co \left( NH _3\right)_5 Cl ^{ Cl } Cl _2\right.$ are:

A

3 and 5

B

2 and 6

C

2 and 8

D

3 and 6

Solution

$\left[ Co \left( NH _3\right)_5 Cl \right] Cl _2$
Oxidation number of $Co$ is $+3$.
So primary valency is $3$ .
It is an octahedral complex so secondary valency $6$
or Co-ordination number $6$ .

Q19. Statement I : For colloidal particles, the values of colligative properties are of small order as compared to values shown by true solutions at same concentration.
Statement II : For colloidal particles, the potential difference between the fixed layer and the diffused layer of same charges is called the electrokinetic potential or zeta potential.
In the light of the above statements, choose the correct answer from the options given below

A

Statement I is false but Statement II is true

B

Both Statement I and Statement II are true

C

Statement I is true but Statement II is false

D

Both Statement I and Statement II are false

Solution

Statement I : For colloidal particles, the values of colligative properties are of small order as compared to values shown by true solutions at same concentration. : True
Statement II : For colloidal particles, the potential difference between the fixed layer and the diffused layer of same charges is called the electrokinetic potential or zeta potential. : True

Q20. ' $A$' and ' $B$ ' formed in the following set of reactions are:

A

B

C

D

Q21. Uracil is a base present in RNA with the following structure. $\%$ of $N$ in uracil is ___

Answer: 25

Solution

Mol. Wt of $C _4 N _2 H _4 O _2=112$
$\% N =\frac{28}{112} \times 100=25 \%$

Q22. If wavelength of the first line of the Paschen series of hydrogen atom is _____ nm, then the wavelength of the second line of this series is nm. (Nearest integer)

Answer: 492

Solution

$\frac{1}{\left(\lambda_1\right)_{ P }}= R _{ H } Z ^2\left(\frac{1}{9}-\frac{1}{16}\right)$
$ \frac{1}{\left(\lambda_2\right)_{ P }}= R _{ H } Z ^2\left(\frac{1}{9}-\frac{1}{25}\right) $
$ \frac{\left(\lambda_2\right)_{ P }}{\left(\lambda_1\right)_{ P }}=\frac{\frac{7}{16 \times 9}}{\frac{16}{25 \times 9}}=\frac{25 \times 7}{16 \times 16} $
$ \left(\lambda_2\right)_{ P }=\frac{25 \times 7}{16 \times 16} \times 720$
$\left(\lambda_2\right)_{ P }=492 \,nm $

Q23. At $298 \,K$, a 1 litre solution containing $10\, m\,mol$ of $Cr _2 O _7{ }^{2-}$ and $100\, m\,mol$ of $Cr ^{3+}$ shows a pH of 3.0.
Given: $Cr _2 O _7^{2-} \rightarrow Cr ^{3+} ; E ^{\circ}=1.330 V$
and $\frac{2.303 RT }{ F }=0.059 V$
The potential for the half cell reaction is $x \times 10^{-3} V$. The value of $x$ is ___

Answer: 917

Solution

$ Cr _2 O _7^{2-}+14 H ^{+}+6 e ^{-} \rightarrow 2 Cr ^{3+}+7 H _2 O$
$E =1.33-\frac{0.059}{6} \log \frac{(0.1)^2}{\left(10^{-2}\right)\left(10^{-3}\right)^{14}} $
$ E =1.33-\frac{0.059}{6} \times 42=0.917 $
$E =917 \times 10^{-3} $
$ x =917$

Q24. The dissociation constant of acetic acid is $x \times 10^{-5}$. When $25 \,mL$ of $0.2 \,M \,CH _3 COONa$ solution is mixed with $25 \,mL$ of $0.02\, M \,CH _3 COOH$ solution, the $pH$ of the resultant solution is found to be equal to 5 . The value of $x$ is ___

Answer: 10

Solution

Buffer of $HOAc$ and $NaOAc$
$ pH = pKa +\log \frac{0.1}{0.01} $
$ 5= pKa +1 $
$ pKa =4$
$ Ka =10^{-4}$
$ x =10$

Q25. For independent processes at $300\, K$
Process $\Delta H / kJ mol ^{-1}$ $\Delta S / JK ^{-1}$
A -25 -80
B -22 40
C 25 -50
D 22 20
The number of non-spontaneous processes from the following is

Answer: 2

Solution

$ \Delta G =\Delta H - T \Delta S$
$A : \Delta G \left( J mol ^{-1}\right)=-25 \times 10^3+80 \times 300:- ve $
$ B : \Delta G \left( J mol ^{-1}\right)=-22 \times 10^3-40 \times 300:- ve$
$ C : \Delta G \left( J mol ^{-1}\right)=25 \times 10^3+300 \times 50:+ ve$
$ D : \Delta G \left( J mol ^{-1}\right)=22 \times 10^3-20 \times 300:+ ve$
Processes $C$ and $D$ are non-spontaneous.

Q26. Number of moles of $AgCl$ formed in the following reaction is

Answer: 2

Solution

Benzylic and tertiary carbocations are stable

Q27. The d-electronic configuration of $\left[ CoCl _4\right]^{2-}$ in tetrahedral crystal field is $e ^{ m } t _2 ^n$ Sum of "$m$" and "number of unpaired electrons" is

Answer: 7

Solution

$ Co ^{2+}: 3 d ^7 4 s ^0, Cl ^{-}: WFL $
image
Configuration $e ^4 t _2{ }^3: m =4$
Number of unpaired electrons $=3$
So, answer $=7$

Q28. $5 \,g$ of $NaOH$ was dissolved in deionized water to prepare a $450 \,mL$ stock solution. What volume (in $mL$ ) of this solution would be required to prepare $500 \,mL$ of $0.1\, M$ solution?
Given: Molar Mass of $Na, O$ and $H$ is 23,16 and $1 \,g\, mol ^{-1}$ respectively

Answer: 180

Solution

$ M=\frac{5}{40} \times \frac{1000}{450} $
$ M_1 V_1=M_2 V_2 $
$ \left(\frac{5}{40} \times \frac{1000}{450}\right) \times V_1=0.1 \times 500$
$V_1=180$

Q29. The number of correct statement/s from the following is
A. Larger the activation energy, smaller is the value of the rate constant.
B. The higher is the activation energy, higher is the value of the temperature coefficient.
C. At lower temperatures, increase in temperature causes more change in the value of $k$ than at higher temperature
D. A plot of $\ln k$ vs $\frac{1}{T}$ is a straight line with slope equal to $-\frac{E_a}{R}$

Answer: 3

Solution

$A : k =A A ^{-\frac{ Ea }{ RT }}$
As Ea increases k decreases
B : Temperature coefficient $=\frac{ k _{ T +10}}{ k _{ T }}$
image
Option (C) is wrong. $\Delta k$ may be greater or lesser depending on temperature.
$D: \ln k=\ln A-\frac{E a}{R T}$

Q30. When $Fe _{0.93} O$ is heated in presence of oxygen, it converts to $Fe _2 O _3$. The number of correct statement/s from the following is
A. The equivalent weight of $Fe _{0.93} O$ is Molecular wejght
$0.79$
B. The number of moles of $Fe ^{2+}$ and $Fe ^{3+}$ in 1 mole of $Fe _{0.93} O$ is $0.79$ and $0.14$ respectively
C. $Fe _{0.93} O$ is metal deficient with lattice comprising of cubic closed packed arrangement of $O ^{2-}$ ions
D. The $\%$ composition of $Fe ^{2+}$ and $Fe ^{3+}$ in $Fe _{0.93} O$ is $85 \%$ and $15 \%$ respectively

Answer: 4

Solution

A : $Fe _{0.93} O \rightarrow Fe _2 O _3 $
$ nf =\left(3-\frac{200}{93}\right) \times 0.93$
$ nf =0.79 $
B: $2 x+(0.93-x) \times 3=2 $
$ x=0.79 $
$ Fe ^{2+}=0.79, Fe ^{3+}=0.21$
C : Fact
D : $\% Fe ^{2+}=\frac{0.79}{0.93} \times 100=85 \% ; Fe ^{3+}=15 \% $

JEE Main Mathematics Question Paper with Solution 2023 January 24th Shift 1 - Morning

Q1. Let $y=y(x)$ be the solution of the differential equation $x^3 d y+(x y-1) d x=0, x>0$, $y\left(\frac{1}{2}\right)=3- e$. Then $y(1)$ is equal to

A

$2-e$

B

e

C

1

D

3

Solution

$ \frac{d y}{d x}=\frac{1-x y}{x^3}=\frac{1}{x^3}-\frac{y}{x^2} $
$ \frac{d y}{d x}+\frac{y}{x^2}=\frac{1}{x^3} $
$ \text { If }=e^{\int \frac{1}{x^2} d x}=e^{-\frac{1}{x}}$
$y \cdot e^{-\frac{1}{x}}=\int e^{-\frac{1}{x}} \cdot \frac{1}{x^3} d x\left(\text { put }-\frac{1}{x}=t\right) $
$y \cdot e^{-\frac{1}{x}}=-\int e^t \cdot t d t $
$ y=\frac{1}{x}+1+C e^{\frac{1}{x}}$
Where $C$ is constant
Put $x=\frac{1}{2}$
$ 3- e =2+1+ Ce ^2$
$ C =-\frac{1}{ e }$
$y (1)=1$

Q2. The area enclosed by the curves $y^2+4 x=4$ and $y-2 x=2$ is :

A

$ \frac{23}{3}$

B

$\frac{22}{3} $

C

$9$

D

$ \frac{25}{3} $

Solution

image
$ y^2+4 x=4 $
$y^2=-4(x-1) $
$ A=\int\limits_{-4}^2\left(\frac{4-y^2}{4}-\frac{y-2}{2}\right) d y=9$

Q3. Let $\Omega$ be the sample space and $A \subseteq \Omega$ be an event.
Given below are two statements :
(S1): If $P ( A )=0$, then $A =\emptyset$
(S2): If $P(A)=1$, then $A=\Omega$ Then

A

both (S1) and (S2) are true

B

only ( S 1) is true

C

only (S2) is true

D

both (S1) and (S2) are false

Solution

$\Omega=$ sample space
$A =$ be an event
If $P(A)=0 \Rightarrow A=\phi$
If $P ( A )=1 \Rightarrow A =\Omega$
Then both statement are true

Q4. The value of $\displaystyle\sum_{r=0}^{22}{ }^{22} C_r{ }^{23} C_r$ is

A

${ }^{45} C _{24}$

B

${ }^{45} C_{23}$

C

${ }^{44} C _{23}$

D

${ }^{44} C_{22}$

Solution

$\displaystyle \sum_{r=0}^{22}{ }^{22} C _{ r } \cdot{ }^{23} C _{ r }=\displaystyle\sum_{ r =0}^{22}{ }^{22} C _{ r } \cdot{ }^{23} C _{23- r }$
$ ={ }^{45} C _{23}$

Q5. Let $\alpha$ be a root of the equation $(a-c) x^2+(b-a) x+(c-b)=0$ where $a , b , c$ are distinct real numbers such that the matrix $\begin{bmatrix}\alpha^2 & \alpha & 1 \\ 1 & 1 & 1 \\ a & b & c\end{bmatrix}$ is singular. Then, the value of $\frac{(a-c)^2}{(b-a)(c-b)}+\frac{(b-a)^2}{(a-c)(c-b)}+\frac{(c-b)^2}{(a-c)(b-a)}$ is

A

6

B

3

C

9

D

12

Solution

$\Delta=0=\begin{vmatrix}\alpha^2 & \alpha & 1 \\ 1 & 1 & 1 \\ a & b & c\end{vmatrix}$
$\Rightarrow \alpha^2(c-b)-\alpha(c-a)+(b-a)=0$
It is singular when $\alpha=1$
$ \frac{(a-c)^2}{(b-a)(c-b)}+\frac{(b-a)^2}{(a-c)(c-b)}+\frac{(c-b)^2}{(a-c)(b-a)}$
$ \frac{(a-b)^3+(b-c)^3+(c-a)^3}{(a-b)(b-c)(c-a)} $
$ =3 \frac{(a-b)(b-c)(c-a)}{(a-b)(b-c)(c-a)}=3$

Q6. $\displaystyle\lim _{t \rightarrow 0}\left(1^{\frac{1}{\sin ^2 t}}+2^{\frac{1}{\sin ^2 t}}+\ldots+n^{\frac{1}{\sin ^2 t}}\right)^{\sin ^2 t}$ is equal to

A

$n ^2$

B

$n ^2+ n$

C

$n$

D

$\frac{n(n+1)}{2}$

Solution

$ \displaystyle\lim _{t \rightarrow 0}\left(1^{\text{cosec}^2 t}+2^{\text{cosec}^2 t}+\ldots \ldots . .+n^{\text{cosec}^2 t}\right)^{\sin ^2 t} $
$ =\displaystyle\lim _{t \rightarrow 0} n\left(\left(\frac{1}{n}\right)^{\text{cosec}^2 t}+\left(\frac{2}{n}\right)^{\text{cosecs}^2 t}+\ldots \ldots . .+1\right)^{\sin ^2 t} $
$ = n $

Q7. The distance of the point $(-1,9,-16)$ from the plane $2 x+3 y-z=5$ measured parallel to the line $\frac{x+4}{3}=\frac{2-y}{4}=\frac{z-3}{12}$ is

A

$20 \sqrt{2}$

B

31

C

$13 \sqrt{2}$

D

26

Solution

Equation of line
$\frac{x+1}{3}=\frac{y-9}{-4}=\frac{z+16}{12}$
G.P on line $(3 \lambda-1,-4 \lambda+9,12 \lambda-16)$
point of intersection of line \& plane
$6 \lambda-2-12 \lambda+27-12 \lambda+16=5$
$\lambda=2$
Point $(5,1,8)$
Distance $=\sqrt{36+64+576}=26$

Q8. Let $N$ denote the number that turns up when a fair die is rolled. If the probability that the system of equations
$ x+y+z=1 $
$ 2 x + Ny +2 z=2 $
$ 3 x +3 y+ N z=3$
has unique solution is $\frac{k}{6}$, then the sum of value of $k$ and all possible values of $N$ is

A

18

B

19

C

20

D

21

Solution

$ x+y+z=1$
$ 2 x+N y+2 z=2$
$ 3 x+3 y+N z=3$
$\Delta=\begin{vmatrix}1 & 1 & 1 \\2 & N & 2 \\3 & 3 & N\end{vmatrix}$
$ =( N -2)( N -3)$
For unique solution $\Delta \neq 0$
So $N \neq 2,3$
$\Rightarrow P ($ system has unique solution $)=\frac{4}{6}$
So $k =4$
Therefore sum $=4+1+4+5+6=20$

Q9. Let $f(x)=\begin{cases}x^2 \sin \left(\frac{1}{x}\right) & , x \neq 0 \\ 0 & , x=0\end{cases}$ Then at $x=0$

A

$f$ is continuous but not differentiable

B

$f$ is continuous but $f^{\prime}$ is not continuous

C

$f^{\prime}$ is continuous but not differentiable

D

$f$ and $f^{\prime}$ both are continuous

Solution

Continuity of $ f(x): f\left(0^{+}\right)=h^2 \cdot \sin \frac{1}{h}=0$
$ f\left(0^{-}\right)=(-h)^2 \cdot \sin \left(\frac{-1}{h}\right)=0 $
$ f(0)=0 $
$ f(x) $ is continuous
$ f^{\prime}\left(0^{+}\right)=\displaystyle\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\frac{h^2 \cdot \sin \left(\frac{1}{h}\right)-0}{h}=0 $
$f^{\prime}\left(0^{-}\right)=\displaystyle\lim _{h \rightarrow 0} \frac{f(0-h)-f(0)}{-h}=\frac{h^2 \cdot \sin \left(\frac{1}{-h}\right)-0}{-h}=0$
$f(x)$ is differentiable.
$f^{\prime}(x)=2 x \cdot \sin \left(\frac{1}{x}\right)+x^2 \cdot \cos \left(\frac{1}{x}\right) \cdot \frac{-1}{x^2}$
$f^{\prime}(x)=\begin{cases}2 x \cdot \sin \left(\frac{1}{x}\right)-\cos \left(\frac{1}{x}\right), & x \neq 0 \\ 0, & x=0\end{cases}$
$\Rightarrow f^{\prime}(x)$ is not continuous (as $\cos \left(\frac{1}{x}\right)$ is highly oscillating at $x=0$ )

Q10. Let $P Q R$ be a triangle. The points $A, B$ and $C$ are on the sides $Q R, R P$ and $P Q$ respectively such that $\frac{Q A}{A R}=\frac{R B}{B P}=\frac{P C}{C Q}=\frac{1}{2}$. Then $\frac{A \text { Area }(\triangle P Q R)}{\text { Area }(\triangle A B C)}$ is equal to

A

4

B

3

C

2

D

$\frac{5}{2}$

Solution

Let $P$ is $\overrightarrow{0}, Q$ is $\vec{q}$ and $R$ is $\vec{r}$
$A$ is $\frac{2 \overrightarrow{ q }+\overrightarrow{ r }}{3}, B$ is $\frac{2 \overrightarrow{ r }}{3}$ and $C$ is $\frac{\overrightarrow{ q }}{3}$
Area of $\triangle PQR$ is $=\frac{1}{2}|\overrightarrow{ q } \times \overrightarrow{ r }|$
Area of $\triangle ABC$ is $\frac{1}{2}|\overrightarrow{ AB } \times \overrightarrow{ AC }|$
$\overrightarrow{ AB }=\frac{\overrightarrow{ r }-2 \overrightarrow{ q }}{3}, \overrightarrow{ AC }=\frac{-\overrightarrow{ r }-\overrightarrow{ q }}{3}$
Area of $\triangle ABC =\frac{1}{6}|\overrightarrow{ q } \times r |$ $\frac{\text{Area}(\triangle PQR )}{\text{Area}(\triangle ABC )}=3$

Q11. For three positive integers $p , q , r , x^{p q^2}=y^{y r}=z^{p^2 r }$ and $r = pq +1$ such that $3,3 \log _y x, 3 \log _z y$ $7 \log _x z$ are in A.P. with common difference $\frac{1}{2}$. Then $r-p-q$ is equal to

A

6

B

2

C

12

D

$-6$

Solution

$ pq ^2=\log _{ x } \lambda $
$ qr =\log _{ y } \lambda $
$p ^2 r =\log _{ z } \lambda$
$ \log _{ y } x =\frac{ qr }{ pq ^2}=\frac{ r }{ pq } \ldots \ldots .(1) $
$ \log _{ x } z =\frac{ pq ^2}{ p ^2 r }=\frac{ q ^2}{ pr } \ldots \ldots \ldots(2) $
$ \log _{ z } y =\frac{ p ^2 r }{ qr }=\frac{ p ^2}{ q } \ldots \ldots \ldots(3)$
$3, \frac{3 r }{ pq }, \frac{3 p ^2}{ q }, \frac{7 q ^2}{ pr } \text { in A.P } $
$\frac{3 r }{ pq }-3=\frac{1}{2}$
$ r =\frac{7}{6} pq\ldots \ldots \ldots(4)$
$ r = pq +1 $
$ pq =6\ldots \ldots \ldots(5)$
$ r =7 \ldots\ldots \ldots \ldots(6)$
$\frac{3 p ^2}{ q }=4$
After solving $p=2$ and $q=3$

Q12. $\tan ^{-1}\left(\frac{1+\sqrt{3}}{3+\sqrt{3}}\right)+\sec ^{-1}\left(\sqrt{\frac{8+4 \sqrt{3}}{6+3 \sqrt{3}}}\right)$ is equal to :

A

$\frac{\pi}{2}$

B

$\frac{\pi}{2}$.

C

$\frac{\pi}{6}$

D

$\frac{\pi}{3}$

Solution

$ \tan ^{-1}\left(\frac{1+\sqrt{3}}{3+\sqrt{3}}\right)+\sec ^{-1}\left(\sqrt{\frac{8+4 \sqrt{3}}{6+3 \sqrt{3}}}\right)$
$ =\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)+\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)=\frac{\pi}{3}$

Q13. The equation $x^2-4 x+[x]+3=x[x]$, where $[x]$ denotes the greatest integer function, has :

A

no solution

B

exactly two solutions in $(-\infty, \infty)$

C

a unique solution in $(-\infty, 1)$

D

a unique solution in $(-\infty, \infty)$

Solution

$ x ^2-4 x +[ x ]+3= x [ x ] $
$\Rightarrow x ^2-4 x +3= x [ x ]-[ x ] $
$ \Rightarrow( x -1)( x -3)=[ x ] .( x -1)$
$ \Rightarrow x =1 \text { or } x -3=[ x ]$
$ \Rightarrow x -[ x ]=3$
$ \Rightarrow\{ x \}=3 \text { (Not Possible) }$
Only one solution $x=1$ in $(-\infty, \infty)$

Q14. Let $p , q \in R$ and $(1-\sqrt{3})^{200}=2^{199}(p+i q), t=\sqrt{-1}$ Then $p + q + q ^2$ and $p - q + q ^2$ are roots of the equation.

A

$x^2-4 x+1=0$

B

$x^2+4 x+1=0$

C

$x^2-4 x-1=0$

D

$x^2+4 x-1=0$

Solution

$ (1-\sqrt{3} i )^{200}=2^{199}( p + iq )$
$ 2^{200}\left(\cos \frac{\pi}{3}- i \sin \frac{\pi}{3}\right)^{200}=2^{199}( p + iq ) $
$ 2\left(-\frac{1}{2}- i \frac{\sqrt{3}}{2}\right)= p + iq$
$ p =-1, q =-\sqrt{3} $
$\alpha= p + q + q ^2=2-\sqrt{3}$
$ \beta= p - q + q ^2=2+\sqrt{3} $
$ \alpha+\beta=4 $
$ \alpha \cdot \beta=1 $
equation $x ^2-4 x +1=0$

Q15. If $A$ and $B$ are two non-zero $n \times n$ matrics such that $A ^2+ B = A ^2 B$, then

A

$A ^2= I$ or $B = I$

B

$A ^2 B = BA ^2$

C

$AB = I$

D

$A ^2 B = I$

Solution

$ A ^2+ B = A ^2 B $
$ \left( A ^2- I \right)( B - I )= I $.......(1)
$ A ^2+ B = A ^2 B$
$A ^2( B - I )= B $
$A ^2= B ( B - I )^{-1} $
$ A ^2= B \left( A ^2- I \right) $
$ A ^2= BA A ^2- B $
$ A ^2+ B = BA ^2$
$ A ^2 B = BA ^2$

Q16. Let a tangent to the curve $y^2=24 x$ meet the curve $x y=2$ at the points $A$ and $B$. Then the mid points of such line segments $A B$ lie on a parabola with the

A

length of latus rectum $\frac{3}{2}$

B

length of latus rectum 2

C

directrix $4 x =3$

D

directrix $4 x=-3$

Solution

$ y ^2=24 x$
$ a =6$
$ xy =2 $
$ AB \equiv ty = x +6 t ^2$.......(1)
$ AB \equiv T = S _1 $
$ kx + hy =2 hk $.........(2)
From (1) and (2)
$\frac{ k }{1}=\frac{ h }{- t }=\frac{2 hk }{-6 t ^2}$
$\Rightarrow$ then locus is $y ^2=-3 x$
Therefore directrix is $4 x=3$

Q17. The distance of the point $(7,-3,-4)$ from the plane passing through the points $(2,-3,1),(-1,1,-2)$ and $(3,-4,2)$ is :

A

$5 \sqrt{2}$

B

$4 \sqrt{2}$

C

4

D

5

Solution

$=\begin{vmatrix} x-2 & y+3 & z-1 \\ -3 & 4 & -3 \\ 4 & -5 & 4 \end{vmatrix}=0$
$x-z-1=0$
Distance of $P (7,-3,-4)$ from Plane is
$d =\left|\frac{7+4-1}{\sqrt{2}}\right|=5 \sqrt{2}$

Q18. The compound statement $(-(P \wedge Q)) \vee((-P) \wedge Q) \Rightarrow((-P) \wedge(-Q))$ is equivalent to

A

$((\sim P) \vee Q) \wedge((\sim Q) \vee P)$

B

$(\sim Q) \vee P$

C

$((-P) \vee Q) \wedge(-Q)$

D

$(-P) \vee Q$

Solution

Let $\quad r =(\sim( P \wedge Q )) \vee((\sim P ) \wedge Q ) ; \quad s =$ $((\sim P ) \wedge(\sim Q ))$
P Q $\sim(P \wedge Q)$ $(-P) \wedge Q$ r s $r \to s$
T T F F F F T
T F T F T F F
F T T T T F F
F F T F T T T

Option (A) : $((\sim P ) \vee Q ) \wedge((\sim Q ) \vee P )$
is equivalent to (not of only $P) \wedge($ not of only $Q$ )
$=($ Both $P , Q )$ and (neither P nor $Q )$

Q19. The relation $R =\{(a, b)$ : $\operatorname{gcd}(a, b)=1,2 a \neq b, a, b \in Z\}$ is :

A

reflexive but not symmetric

B

transitive but not reflexive

C

symmetric but not transitive

D

neither symmetric nor transitive

Solution

Reflexive: $( a , a ) \Rightarrow \operatorname{gcd}$ of $( a , a )=1$
Which is not true for every a $\epsilon Z$.
Symmetric:
Take $a =2, b =1 \Rightarrow \operatorname{gcd}(2,1)=1$
Also $2 a =4 \neq b$
Now when $a =1, b =2 \Rightarrow \operatorname{gcd}(1,2)=1$
Also now $2 a =2= b$
Hence $a=2 b$
$\Rightarrow R$ is not Symmetric
Transitive:
Let $a =14, b =19, c =21$
$\text{gcd}(a, b)=1$
$\text{gcd}(b, c)=1$
$\text{gcd}(a, c)=7$
Hence not transitive
$\Rightarrow R$ is neither symmetric nor transitive.

Q20. Let $\vec{u}=\hat{i}-\hat{j}-2 \hat{k}, \vec{v}=2 \hat{i}+\hat{j}-\hat{k}, \vec{v} \cdot \vec{w}=2$ and $\vec{v} \times \vec{w}=\vec{u}+\lambda \vec{v}$. Then $\vec{u} \cdot \vec{w}$ is equal to

A

1

B

2

C

$\frac{3}{2}$

D

$-\frac{2}{3}$

Solution

$\overrightarrow{ u }=(1,-1,-2), \overrightarrow{ v }=(2,1,-1), \overrightarrow{ v } \cdot \overrightarrow{ w }=2$
$ \overrightarrow{ v } \times \overrightarrow{ w }=\overrightarrow{ u }+\lambda \overrightarrow{ v } \ldots \ldots \ldots \ldots \ldots \ldots \ldots(1) $
Taking dot with $ \overrightarrow{ w } \text { in }(1) $
$ \overrightarrow{ w } \cdot(\overrightarrow{ v } \times \overrightarrow{ w })=\overrightarrow{ u } \cdot \overrightarrow{ w }+\lambda \overrightarrow{ v } \cdot \overrightarrow{ w }$
$ \Rightarrow 0=\overrightarrow{ u } \cdot \overrightarrow{ w }+2 \lambda$
Taking dot with $\vec{v}$ in (1)
$ \overrightarrow{ v } \cdot(\overrightarrow{ v } \times \overrightarrow{ w })=\overrightarrow{ u } \cdot \overrightarrow{ v }+\lambda \overrightarrow{ v } \cdot \overrightarrow{ v }$
$ \Rightarrow 0=(2-1+2)+\lambda \cdot(6)$
$ \lambda=-\frac{1}{2} $
$ \Rightarrow \overrightarrow{ u } \cdot \overrightarrow{ w }=-2 \lambda=1$

Q21. Let $\lambda \in R$ and let the equation $E$ be $|x|^2-2|x|+|\lambda-3|=0$. Then the largest element in the set $S=$ $\{x+\lambda: x$ is an integer solution of $E\}$ is

Answer: 5

Solution

$ | x |^2-2| x |+|\lambda-3|=0$
$ | x |^2-2| x |+|\lambda-3|-1=0$
$ (| x |-1)^2+|\lambda-3|=1$
At $\lambda=3, x =0$ and 2 ,
at $\lambda=4$ or 2 ,
then $x =1$ or $-1$
So maximum value of $x+\lambda=5$

Q22. A boy needs to select five courses from 12 available courses, out of which 5 courses are language courses. If he can choose at most two language courses, then the number of ways he can choose five eourses is

Answer: 546

Solution

For at most two language courses
$={ }^5 C _2 \times{ }^7 C _3+{ }^5 C _1 \times{ }^7 C _4+{ }^7 C _5=546$

Q23. The value of $\frac{8}{\pi} \int\limits_0^{\frac{\pi}{2}} \frac{(\cos x)^{2023}}{(\sin x)^{2023}+(\cos x)^{2023}} d x$ is

Answer: 2

Solution

$I=\frac{8}{\pi} \int\limits_0^{\frac{\pi}{2}} \frac{(\cos x)^{2023}}{(\sin x)^{2023}+(\cos x)^{2023}} d x$......(1)
Using $\int\limits_0^a f(x) d x=\int\limits_0^a f(a-x) d x$
$I=\frac{8}{\pi} \int\limits_0^{\frac{\pi}{2}} \frac{(\sin x)^{2023}}{(\sin x)^{2023}+(\cos x)^{2023}} d x$........(2)
Adding (1) & (2)
$ 2 I =\frac{8}{\pi} \int\limits_0^{\frac{\pi}{2}} 1 dx$
$ I =2$

Q24. The shortest distance between the lines $\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-6}{2}$ and $\frac{x-6}{3}=\frac{1-y}{2}=\frac{z+8}{0}$ is equal to

Answer: 14

Solution

Shortest distance between the lines
$=\frac{\begin{vmatrix}4 & 2 & -14 \\ 3 & 2 & 2 \\ 3 & -2 & 0\end{vmatrix}}{\begin{vmatrix}\hat{i} & \hat{ j } & \hat{ k } \\ 3 & 2 & 2 \\ 3 & -2 & 0\end{vmatrix}}$
$=\frac{16+12+168}{|-4 \hat{i}+6 \hat{j}-12 \hat{k}|}=\frac{196}{14}=14$

Q25. The $4^{\text {th }}$ term of $G P$ is $S 00$ and its common ratio is $\frac{1}{m}, m \in N$. Let $S_n$ denote the sum of the first $n$ terms of this GP. If $S_6>S_5+1$ and $S_7< S_6+\frac{1}{2}$, then the number of possible values of $m$ is

Answer: 12

Solution

$T _4=500 $ where $a =$ first term,
$r =\text { common ratio }=\frac{1}{ m }, m \in N$
$ a r^3=500 $
$ \frac{a}{m^3}=500 $
$ S_n-S_{n-1}=a r^{n-1}$
$ S_6>S_5+1$
and $S _7- S _6< \frac{1}{2}$
$S _6- S _5>1 \,\,\,\,\,\frac{ a }{ m ^6}<\frac{1}{2}$
$ar ^5>1 \,\,\,\, m ^3>10^3$
$\frac{500}{ m ^2}>1 \,\,\,\,\, m >10$...(2)
$m ^2< 500$.........(1)
From (1) and (2)
$m =11,12,13 \ldots \ldots \ldots \ldots ., 22$
So number of possible values of $m$ is $12$

Q26. Let $C$ be the largest circle centred at $(2,0)$ and inscribed in the ellipse $\frac{x^2}{36}+\frac{y^2}{16}=1$. If $(1, a)$ lies on $C$, then $10 \alpha^2$ is equal to

Answer: 118

Solution

image
Equation of normal of ellipse $\frac{x^2}{36}+\frac{y^2}{16}=1$ at any point $P (6 \cos \theta, 4 \sin \theta)$ is
$3 \sec \theta x-2 \operatorname{cosec} \theta y=10$ this normal is also the normal of the circle passing through the point $(2,0)$ So,
$6 \sec \theta=10$ or $\sin \theta=0$ (Not possible) $\cos \theta=\frac{3}{5}$ and $\sin \theta=\frac{4}{5}$ so point $P =\left(\frac{18}{5}, \frac{16}{5}\right)$
So the largest radius of circle
$r=\frac{\sqrt{320}}{5}$
So the equation of circle $(x-2)^2+y^2=\frac{64}{5}$
Passing it through $(1, \alpha)$
Then $\alpha^2=\frac{59}{5}$
$10 \alpha^2=118$

Q27. Let a tangent to the curve $9 x^2+16 y^2=144$ intersect the coordinate axes at the points $A$ and $B$. Then, the mininum length of the line segment $AB$ is

Answer: 7

Solution

Equation of tangent at point $P (4 \cos \theta, 3 \sin \theta)$ is $\frac{ x \cos \theta}{4}+\frac{ y \sin \theta}{3}=1$
So $A$ is $(4 \sec \theta, 0)$ and point $B$ is $(0,3 \operatorname{cosec} \theta)$
Length $A B =\sqrt{16 \sec ^2 \theta+9 \operatorname{cosec}^2 \theta}$ $=\sqrt{25+16 \tan ^2 \theta+9 \cot ^2 \theta} \geq 7$

Q28. Suppose $\displaystyle\sum_{r=0}^{2023} r^{22023} C_r=2023 \times \alpha \times 2^{2022}$. Then the value of $\alpha$ is

Answer: 1012

Solution

using result
$\displaystyle\sum_{ r =0}^{ n } r ^2\,\,{ }^{ n } C _{ r }= n ( n +1) \cdot 2^{ n -2}$
Then $\displaystyle\sum_{ r =0}^{2023} r ^2\,\,{ }^{2023} C _{ r }=2023 \times 2024 \times 2^{2021}$
$ =2023 \times \alpha \times 2^{2022} \text { So, } $
$ \Rightarrow \alpha=1012$

Q29. The value of $12 \int\limits_0^3\left|x^2-3 x+2\right| d x$ is

Answer: 22

Solution

$ 12 \int\limits_0^3\left| x ^2-3 x +2\right| dx $
$ =12 \int\limits_0^3\left|\left( x -\frac{3}{2}\right)^2-\frac{1}{4}\right| dx$
$ \text { If } x -\frac{3}{2}= t $
$ dx - dt$
$=24 \int\limits_0^{3 / 2}\left| t ^2-\frac{1}{4}\right| dt $
$ =24\left[-\int\limits_0^{1 / 2}\left( t ^2-\frac{1}{4}\right) dt +\int\limits_{1 / 2}^{3 / 2}\left( t ^2-\frac{1}{4}\right) dt \right]=22$

Q30. The number of 9 digit numbers, that can be fonned using all the digits of the number 123412341 so that the even digits occupy only even places, is

Answer: 60

Solution

Even digits occupy at even places
$ \frac{4 !}{2 ! 2 !} \times \frac{5 !}{2 ! 3 !}=\frac{24 \times 120}{4 \times 12}=60$