JEE Main Physics Question Paper with Solution 2023 January 29th Shift 1 - Morning
A
$\left(3.6 \times 10^6\right)$
B
$\left(7.5 \times 10^6\right)$
C
$\left(1.8 \times 10^6\right)$
D
$\left(8.4 \times 10^6\right)$
Solution
$V _{ n } \propto \frac{ Z }{ n } $
$ Z =1,$
$\therefore V _{ n } \propto \frac{1}{ n } $
$\therefore \frac{ V _3}{ V _7}=\frac{7}{3} $
$ \therefore V _3=\frac{7}{3} V _7 $
$=\frac{7}{3} \times 3.6 \times 10^6 m / s $
$=8.4 \times 10^6\,m / s $
A
$10\, V$
B
$5 \, V$
C
$20 \, V$
D
$15 \, V$
Solution
$ A _{ c }+ A _{ m }=120 $
$A_c-A_m=80 $
$ \therefore \overline{ A _{ c }}=100 $
$ A_m=20 $
Modulation index $=\frac{20}{100}=\frac{1}{5} $
Amplitude of each sideband
$ = A _{ c } \frac{(\text { mod ulation index })}{2} $
$ =100 \times \frac{1}{10}=10 volt $
A
$\alpha-\frac{\gamma^2}{3 \beta}$
B
$\beta-\frac{\alpha^2}{3 \gamma}$
C
$\alpha-\frac{\beta^2}{3 \gamma}$
D
$\alpha-\frac{3 \beta^2}{\gamma}$
Solution
$ Q =\left(\alpha t -\beta t ^2+\gamma t ^3\right) $
$ i =\frac{ dQ }{ dt }=\left(\alpha-2 \beta t +3 \gamma t ^2\right)$
$ \frac{ di }{ dt }=(3 \gamma t -2 \beta)=0$
$\Rightarrow t =\frac{\beta}{3 \gamma} $
$ i =\left(\alpha-2 \beta t +3 \gamma t ^2\right)=\left(\alpha-\frac{\beta^2}{3 \gamma}\right)$
A
$\sigma=\frac{3 K+2 \eta}{6 K+2 \eta}$
B
$\sigma=\frac{6 K-2 \eta}{3 K-2 \eta}$
C
$\sigma=\frac{3 K-2 \eta}{6 K+2 \eta}$
D
$\sigma=\frac{6 K+2 \eta}{3 K-2 \eta}$
Solution
$Y=3 \eta(1+\sigma) $
$ Y=3 K(1-\sigma) $
$ \Rightarrow 2 \eta(1+\sigma)=3 K(1-2 \sigma)$
$ \Rightarrow \sigma=\left(\frac{3 K-2 \eta}{6 K+2 \eta}\right)$
A
B
C
D
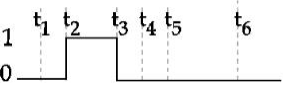
Solution
$ (\overline{ A \cdot A })=\overline{ A }$
$ \overline{ B \cdot B }=\overline{ B } $
$ (\overline{\overline{ A } \cdot \overline{ B }})= A + B$
OR Gate
A
$2 \times 10^{-17} kg \,m / s$
B
$1 \times 10^{-17} kg \,m / s$
C
$3 \times 10^{-17} kg\, m / s$
D
$0.5 \times 10^{-17} kg \,m / s$
Solution
$ \text { Momentum }=\frac{\text { Energy }}{ C }$
$ =\frac{\text { Power } \times \text { time }}{ C } $
$=\frac{\left(20 \times 10^{-3} w \right)\left(300 \times 10^{-9} s \right)}{3 \times 10^8 m / s } $
$ =2 \times 10^{-17} \,kg - m / s $
A
$\frac{5}{3}$
B
$\frac{9}{4}$
C
$\frac{5}{6}$
D
$\frac{4}{3}$
Solution

$ \frac{Q_1^{\prime}}{4 \pi \varepsilon_0 R}=\frac{Q_2^{\prime}}{4 \pi \varepsilon_0(2 R)} $
$ \therefore Q_2^{\prime}=2 Q_1^{\prime} $
$Q_1^{\prime}+Q_2^{\prime}=Q_1+Q_2 $
$ \therefore \frac{Q_2^{\prime}}{2}+Q_2^{\prime}=20 \pi R^2 \sigma $
$\frac{3}{2} Q_2^{\prime}=20 \pi R^2 \sigma $
$ \therefore \frac{Q_2^{\prime}}{4 \pi(2 R)^2}=\frac{2}{3} \cdot \frac{20 \pi R^2 \sigma}{16 \pi R^2} $
$ \therefore \frac{\sigma^{\prime}}{\sigma}=\frac{5}{6}$
A
$1: 2$
B
$1: 3$
C
$1: 1$
D
$1: \sqrt{2}$
Solution
$ P=\frac{R}{Z} \Rightarrow P_1=\frac{R}{\sqrt{R^2+X_L^2}}=\frac{R}{R \sqrt{2}}\left(\text { as } X_L=R\right)$
$P_1=\frac{1}{\sqrt{2}} $
$ P_2=\frac{R}{\sqrt{R^2+\left(X_L-X_L\right)^2}}=P_2=1 $
$ \frac{P_1}{P_2}=\frac{1}{\sqrt{2}}$
A
A- I, B-III, C-IV, D-II
B
A- II, B-IV, C-III, D-I
C
A- II, B-III, C-IV, D-I
D
A- I, B-II, C-III, D-IV
Solution
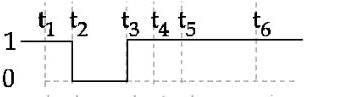
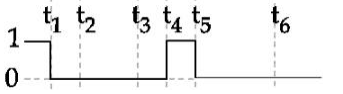
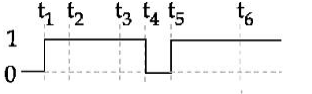
$\frac{ dx }{ dt }=$ slope $\geq 0$ always increasing
(A - II)
$\frac{ dx }{ dt }<0$; and at $t \rightarrow \infty \frac{ dx }{ dt } \rightarrow 0$
(B - IV)
$\frac{ dx }{ dt }>0$ for first half $\frac{ dx }{ dt }<0$ for second half.
(C - III)
$\frac{ dx }{ dt }=\text { constant }$
(D - I)
A
$c$ and $b$
B
$a$ and $b$
C
$b$ and $c$
D
$c$ and $a$
Solution
$ \left|\frac{ d \overrightarrow{ p }}{ dt }\right|=|\overrightarrow{ F }| \Rightarrow \frac{ d \overrightarrow{ p }}{ dt }=$Slope of curve
max slope (c)
min slope (b)
A
10 Cm
B
40 Cm
C
30 Cm
D
50 Cm
Solution
$ \frac{1}{ v }-\frac{1}{ u }=\frac{1}{ f } $
$ P =2 D =2 m ^{-1}$
$ \Rightarrow \frac{1}{ f }=\frac{2}{100} \,cm ^{-1} $
$ \frac{1}{ V }-\left(-\frac{1}{25}\right)=\frac{2}{100} $
$ \Rightarrow \frac{1}{ V }=\frac{1}{50}-\frac{1}{25} $
$ \Rightarrow V =-50 \,cm $
A
$0.20$
B
$0.5$
C
$0.10$
D
$0.05$
Solution
$ h =\frac{2 S \cos \theta}{ r \rho g }$
$\therefore \frac{ h _1}{ h _2} =\frac{ S _1}{ S _2} \frac{\rho_2}{\rho_1} $
$\frac{5}{ h _2} =\left[\frac{1}{2}\right]\left[\frac{2}{1}\right] \Rightarrow h _2=5 cm =0.05 m$
$\{$Info about angle of contact not there so most appropriate is 3 $\}$
A
C and D only
B
B and D only
C
A and E only
D
C and E only
Solution
Sol. $dQ = dU + dW $
$\Rightarrow dU = nC _{ V } dT$
$dU =0 $ (for isothermal)
$\therefore U =$ constant
Also $dQ >0 $ (supplied)
Hence $d W>0$
A
$2 N _{ A } I _{ A }= N _{ B } I _{ B }$
B
$N _{ A }=2 N _{ B }$
C
$N _{ A } I _{ A }=4 N _{ B } I _{ B }$
D
$4 N _{ A } I _{ A }= N _{ B } I _{ B }$
Solution
Sol. $M =$ NIA
$ M _{ A }= M _{ B } $
$\therefore N _{ A } I _{ A } A _{ A }= N _{ B } I _{ B } A _{ B } $
$\therefore N _{ A } I _{ A } \pi(0.1)^2= N _{ B } I _{ B } \pi(0.2)^2 $
$\therefore N _{ A } I _{ A }=4 N _{ B } I _{ B }$
A
$\frac{1}{10} V$
B
$1 V$
C
$100 V$
D
$10 V$
Solution
$ F _{ m }= mg$
$\therefore \text { ILB }= mg $
$ \therefore \left(\frac{ V }{ R }\right) LB = mg$
$ \therefore V =\frac{ mgR }{ LB } $
$ =\frac{\left(1 \times 10^{-3} kg \right)\left(10 m / s ^2\right)(10 \Omega)}{(0.1 m )\left(10^3 \times 10^{-4} T \right)}=10 \,V $
A
$400\, m / s$
B
$360 \,m / s$
C
$60 \,m / s$
D
$120 \,m / s$
Solution

$ v _1=\frac{30}{\sqrt{\frac{2 h }{ g }}}, v _2=\frac{120}{\sqrt{\frac{2 h }{ g }}} $
$ (0.01) u =(0.2) \frac{30 \sqrt{ g }}{\sqrt{2 h }}+(0.01) \frac{120 \sqrt{ g }}{\sqrt{2 h }}$
$ u =300+60=360 \,ms ^{-1}$
A
$3 T ^2$
B
$\frac{3}{ T ^2}$
C
$\frac{3}{ T ^3}$
D
$\frac{3}{ T }$
Solution
$ PT ^2=$ constant, Using
$ PV = nRT $
$ P =\frac{ nRT }{ V } $
$ PT ^2=\frac{ nRT }{ V } \times T ^2=\text { constant }$
$ \Rightarrow T ^3= KV $
$ \text { So, } \frac{ d }{ dT }( KV )=3 T ^2$
$\Rightarrow \frac{ KdV }{ dT }=3 T ^2 $
$ \Rightarrow dV =\frac{3 T ^2}{ K } dT $
$ dV = V \gamma dT $
$\Rightarrow \gamma V=\frac{3 T^2}{K} $
$\Rightarrow \gamma=\frac{3 T^2}{K V}=\frac{3 T^2}{ T ^3}=\frac{3}{T}$
A
$4\, m / s$
B
0
C
$0.25 \,m / s$
D
$2\, m / s$
Solution
The velocities will be interchanged after collision.
Speed of $P$ just before collision $=\sqrt{2 gh }$
$=\sqrt{2 \times 10 \times 0.2}=2\, m / s$
A
$Nm ^2 C ^{-1} ; Nm ^3 C ^{-1}$
B
$Nm ^3 C ; Nm ^2 C$
C
$Nm ^2 C ; Nm ^3 C$
D
$Nm ^3 C ^{-1} ; Nm ^2 C ^{-1}$
Solution
$ \vec{ E }=\frac{ A }{ x ^2} \hat{ i }+\frac{ B }{ y ^3} \hat{ j } $
$ {\left[\frac{ A }{ x ^2}\right]= NC ^{-1} \Rightarrow[ A ]= Nm ^2 C ^{-1}} $
${\left[\frac{ B }{ y ^3}\right]= NC ^{-1} \Rightarrow[ B ]= Nm ^3 C ^{-1}}$
A
11
B
10
C
12
D
9
Solution
$ -\frac{ dV }{ dr }=-\frac{ k }{ r ^2} \Rightarrow \int\limits_{10}^{ V } dV =\int\limits_2^3 \frac{ k }{ r ^2} dr $
$ V -10= k \left[\frac{1}{2}-\frac{1}{3}\right] $
$V -10=\frac{ k }{6} \Rightarrow V =11 \text { volts }$
Answer: 32
Solution
$ \frac{1}{ v }+\frac{1}{ u }=\frac{1}{ f } $
$ \frac{-1}{120}-\frac{1}{40}=\frac{1}{ f }, \,\,\, f =-30\, cm$
Now,
$\frac{-1}{v^2} d v-\frac{1}{u^2} d u=-\frac{1}{f^2} d f$
Also $dv = du =\frac{1}{20} cm$
$\therefore\frac{\frac{1}{20}}{(120)^2}+\frac{\frac{1}{20}}{(40)^2}=\frac{ df }{(30)^2}$
On solving
$ df =\frac{1}{32} \,cm $
$ \therefore k =32$
Answer: 22
Solution
Least count $=\frac{\text { Pitch }}{\text { No. of circular divisions }}$
$=\frac{0.5 mm }{100}$
Least count $=5 \times 10^{-3} mm$
Positive Error $= MSR + CSR ( LC )$
$=0 mm +6\left(5 \times 10^{-3} mm \right)$
Reading of Diameter $=$ MSR $+\operatorname{CSR}( LC )-$
Positive zero error
$=4 \times 0.5 \,mm +\left(46\left(5 \times 10^{-3}\right)\right)-6\left(5 \times 10^{-3}\right) \,mm$
$=2 \,mm +40 \times 5 \times 10^{-3} mm =2.2 \,mm$
Answer: 3
Solution
$ ( KE )_{\text {Rotational }}=\frac{1}{2} I \omega^2= E $
$ E =\frac{1}{2} \frac{ m \ell^2}{12} \omega^2 $
$ E =\frac{1}{2} \frac{ dA \ell^3}{12} \omega^2 $
$ E =\frac{ dA (2)^3}{24} \omega^2 $
$ \sqrt{\frac{3 E }{ dA }}=\omega $
$ \alpha=3 $
Answer: 50
Solution

$t_{A B}=\frac{x}{5 m / s }$
In motion $BC$
$x = d _1+ d _2$
where $d _1 \& d _2$ we the distance travelled with $10 \,m / s$ and $15 \,m / s$ respectively in equal time intervals
$ \frac{ t ^{\prime}}{2} \text { each }$
$ d _1=\frac{10 t }{2}, d _2=\frac{15 t }{2}$
$ d _1+ d _2= x =\frac{ t }{2}(10+15)=\frac{25 t }{2}$
$< v >=\frac{2 x }{\frac{ x }{5}+\frac{2 x }{25}}=\frac{2 \times 25}{5+2}=\frac{50}{7} m / s$
Answer: 30
Solution

$\frac{ dI }{ dt }=-1 \frac{ A }{ \sec }$
$ V_A-I R-L \frac{d I}{d t}-12=V_B $
$ V_A-2 \times 12-6(-1)-12=V_B $
$ V_A-V_B=36-6=30 $ volt
Answer: 10
Solution

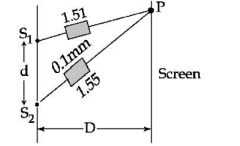
Path difference at $P$ be $\Delta x$
$\Delta x =\left(\mu_2-\mu_1\right) t $
$ =(1.55-1.51) 0.1 \,mm$
$ =0.04 \times 10^{-4} $
$\Delta x =4 \times 10^{-6}=4 \,\mu m$
$y =\frac{\Delta xD }{ d }=4 \times 10^{-6} \frac{ D }{ d }$
$\{ y$ is the distance of central maxima from geometric center $\}$
$\underset{(\beta)}{\text { fringe width }}=\frac{\lambda D}{d}=4 \times 10^{-6} m \frac{D}{ d }=4 \mu m \frac{D}{ d }$
$\therefore $ Central bright fringe spot will shift by ' $x$ '
Number of shift $=\frac{y}{\beta}$
$=\frac{4 \times 10^{-6} D / d }{4 \times 10^{-7} D / d }=10 $
Answer: 8
Solution
$ x = A \sin (\omega t ) $
$ U _{( x )}=\frac{1}{2} kx ^2 $
$ \frac{ dU }{ dt }=\frac{1}{2} k 2 x \frac{ dx }{ dt } $
$ = kA ^2 \omega \sin \omega t \cos \omega t \times \frac{2}{2}$
$\left(\frac{ dU }{ dt }\right)_{\max }=\frac{ kA ^2 \omega}{2}(\sin 2 \omega t)_{\max } $
$ 2 \omega t=\frac{\pi}{2} \Rightarrow t=\frac{\pi}{4} \omega=\frac{T}{8} \Rightarrow \beta=8$
Answer: 225
Solution

Common potential will be developed across both capacitors by $kVL$
Total charge on left plates of capacitors should be conserved.
$\therefore 90 \,mc +0=2 cv _0 $
$ cv _0=45\, mc$

Heat dissipated $= U _{ i }- U _{ f }$ [Change in energy stored in the capacitors]
$=\frac{1}{2} \frac{(90 mc )^2}{900 \mu F }-2 \times \frac{1}{2} \frac{(45 mc )^2}{900 \mu F }\left[ U =\frac{ Q ^2}{2 c }\right] $
$ =\frac{1}{2 \times 900 \times 10^{-6}}(8100-4050) \times 10^{-6}$
$ =2.25$ Joule
OR
$ \text { Heat }=\frac{1}{2} \frac{ C _1 C _2}{ C _1+ C _2}\left( V _1- V _2\right)^2 $
$=\frac{1}{2} \frac{ C ^2}{2 C }(100-0)^2$
$ =\frac{1}{2} \frac{900 \times 10^{-6}}{2} \times 10^4=\frac{9}{4} \text { Joule }=2.25$ Joule
Answer: 4
Solution

$ \text { Force }=\int PdA \cos \theta$
$ =\frac{2 I }{ C } \int dA \cos \theta=\frac{2 I }{ C } \pi R ^2=2 \frac{ p _0}{4 \pi R ^2} \cdot \frac{\pi R ^2}{ C } $
$ =\frac{ p _0}{2 C }=\frac{24}{2 \times 3 \times 10^8}=4 \times 10^{-8} N$
Answer: 1
Solution

Junction law at $A$,
$\frac{x-(y+5)}{1}+\frac{x-2}{2}+\frac{x-0}{2}=0$....(1)
Junction law at $B$,
$\frac{ y +5- x }{1}+\frac{ y -0}{1}+\frac{ y -2}{1}=0$....(2)
On solving equation (1) and Equation (2) $x =3$
$\& y =0$
At $D$ junction
$I _1 = i _1+ i _2 $
$I _1 =\frac{ y -0}{1}+\frac{ x -0}{2}$
$ =\frac{0-0}{1}+\frac{3-0}{2} $
$I _1 =15 A$
JEE Main Chemistry Question Paper with Solution 2023 January 29th Shift 1 - Morning
A
A, C, D only
B
C, D, E only
C
B, E, A only
D
A, B, D only
Solution

- Two lone pair one oxygen
- Molecule is ' $v$ ' shaped
- Bond angle is less than $104.5^{\circ}\left(102^{\circ}\right)$
- O.S. of 'O' is $+2$
A
$LiH$ and $Al ( OH )_3$
B
$LiCl$ and $Al _2 H _6$
C
$LiCl , Al$ and $H _2$
D
$LiH$ and $Al _2 Cl _6$
Solution
$8 LiH + Al _2 Cl _6 \longrightarrow 2 LiAlH _4+6 LiCl$
A
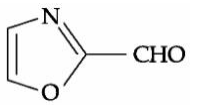
B
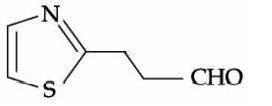
C
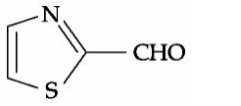
D
Solution
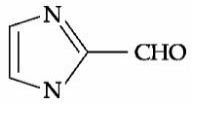
Aromatic aldehydes do not give Fehling's test.. Both nitrogen and sulfur must be present to obtain blood red colour Sodium nitroprusside gives blood red colour with S & N.
A
red
B
blue
C
green
D
black
Solution
$Cr _2 O _7^{2-}+ SO _3^{2-} \xrightarrow{ H ^{+}} \underset{\text{ Green }}{ Cr ^{3+}}+ SO _4^{2-}$
A
$H _{ C }> H _{ D }> H _{ A }> H _{ B } $
B
$ H _{ C }> H _{ D }> H _{ B }> H _{ A } $
C
$ H _{ C }> H _{ A }> H _{ D }> H _{ B } $
D
$ H _{ D }> H _{ C }> H _{ B }> H _{ A }$
Solution
acidity of an acid depends upon the stability of its conjugate base
A
$N , O _2 \& O _3$
B
$NO , O \& O _3$
C
$O , N _2 O \& NO$
D
$O , NO \& NO _3^{-}$
Solution
$NO _{2 g } \stackrel{ hv }{\longrightarrow} \underset{(A)}{NO _{ g }}+\underset{(B)}{ O _{ g }}$
$\underset{(B)}{O _{ g }}+ O _{2 g } \rightleftharpoons \underset{(C)}{O _{3 g }}$
$\underset{(A)}{ NO _{ g }}+\underset{\text { (C) }}{ O _{3 g }} \longrightarrow NO _{2 g }+ O _{2 g }$
A
Ranitidine
B
Brompheniramine
C
Terfenadine
D
Meprobamate
Solution
1. Ranitidine: Antacid
2. Meprobamate: Tranquilizer
3. Terfenadine: Antihistamine
4. Brompheniramine: Antihistamine
A
Dacron
B
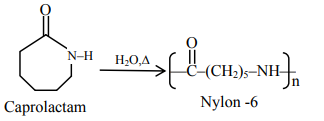
Nylon 6
C
Teflon
D
Nylon 6, 6
A
$S ^{2-}< NH _3<$ en $< CO < C _2 O _4^2$
B
$NH _3< en < CO < S ^{2-}< C _2 O _4^2$
C
$CO <$ en $< NH _3< C _2 O _4^2< S ^{2-}$
D
$S ^{2-}< C _2 O _4^2< NH _3< en < CO$
Solution
The increasing order of field strength of ligands (according to spectrochemical series)
$S ^{2-}< C _2 O _4^{2-}< NH _3< en < CO$
A
$Z n^{2+}$
B
$Fe ^{3+}$
C
$Ni ^{2+}$
D
$Co ^{2+}$
Solution
$ Zn ^{2+}, Co ^{2+}, Ni ^{2+}= IV ^{\text {th }} \text { Group } $
$ Fe ^{3+}= III ^{ rd } \text { Group }$
A
A - IV, B - I, C - II, D - III
B
A - II, B - I, C - IV, D - III
C
A - II, B - III, C - IV, D - I
D
A - IV, B - III, C - II, D - I
Solution
$IF _7 $ zero lone pair
$ICl _4^{-} $ two lone pair
$XeF _6 $ one lone pair
$XeF _2 $ three lone pair
A
Both (A) and (R) are true but $( R )$ is not the correct explanation of (A)
B
(A) is false but (R) is true
C
(A) is true but (R) is false
D
Both (A) and (R) are true and (R) is the correct explanation of (A)
Solution
Seliwanoff 's test is a differentiating test for Ketose and aldose. This test relies on the principle that the keto hexose are more rapidly dehydrated to form 5-hydroxy methyl furfural when heated in acidic medium which on condensation with resorcinol, Cherry red or brown red coloured complex is formed rapidly indicating a positive test
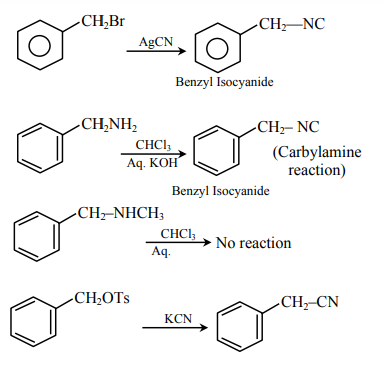
Q14. Benzyl isocyanide can be obtained by :

Choose the correct answer from the options given below :
A
Only B
B
B and C
C
A and B
D
A and D
A
remove $FeO$ as $FeSiO _3$
B
separate $CuO$ as $CuSiO _3$
C
decrease the temperature needed for roasting of $Cu _2 S$
D
remove calcium as $CaSiO _3$
Solution
The copper ore contains iron, it is mixed with silica before heating in reverberatory furnace. $FeO$ slags off as $FeSiO _3$.
$FeO + SiO _2 \longrightarrow FeSiO _3$
A
A and B
B
A only
C
B only
D
B and C
Solution
Due to high hydration energy $Be ^{2+}$ and $Mg ^{2+}$, $BeSO _4$ and $MgSO _4$ are readily soluble in water.
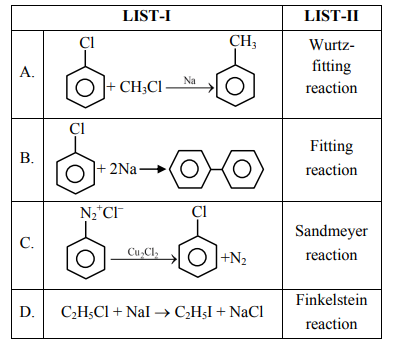
A
A - III, B - II, C - IV, D - I
B
A - II, B - I, C - IV, D - III
C
A - IV, B - II, C - III, D - I
D
A - II, B - I, C - III, D - IV
A
Both (A) and (R) are true and (R) is the correct explanation of (A)
B
Both $(A)$ and $(R)$ are true but $(R)$ is not the correct explanation of $(A)$
C
(A) is false but (R) is tirle
D
(A) is true but (R) is false
Solution
Silica gel prevents water corrosion (rusting) and instrument malfunction by adsorbing moisture from the air
A
A and C Only
B
B and D Only
C
A and B Only
D
C and D Only
Solution
Cis - Platin is used in chemotherapy to inhibits the growth of tumors. (cis $\left[ Pt \left( NH _3\right)_2 Cl _2\right]$ )
A
A - IV, B - II, C - I, D - III
B
A - IV, B - III, C - II, D - I
C
A - I, B - III, C - IV, D - II
D
A - II, B - IV, C - I, D - III
Solution
Atomic number $ \,\,\,$Block
37 (K) $ \,\,\,$s-block
78 (Pt) $ \,\,\,$d-block
52 (Te)$ \,\,\,$ p-block
65 (Tb)$ \,\,\,$ f-block
Answer: 0
Solution
For ideal gas $U=f(T)$
and for isothermal process, $\Delta U =0$
Answer: 100
Solution
$\Delta T _{ b } =373.52-373 $
$ =0.52$
$\Delta T _{ b } = Kb \cdot m$
$0.52 =0.52 \times \frac{2}{\text { Molar Mass }} \times \frac{1}{20 \times 10^{-3}}$
Molar Mass $=100\, g / mol$
Answer: 10
Solution
$ Pt _{( s )}\left| H _2( g , 1 atm )\right| H ^{+}( aq , 1 M ) \| Fe ^{3+}( aq ), Fe ^{2+}( aq )| Pt |( s ) $
$ \text { at anode } H _2 \longrightarrow 2 H ^{+}+2 e ^{-} $
$ \text {At cathode } Fe _{ aq }^{3+}+ e ^{-} \longrightarrow Fe _{ aq }^{2+}$
$E ^{\circ}= E _{ H _2 \mid H ^{+}}^{\circ}+ E _{ Fe ^{3+} \mid Fe ^{2+}}^{\circ}=0 \cdot 771 V $
$ E = E ^{\circ}-\frac{0 \cdot 06}{1} \log \frac{ Fe ^{2+}}{ Fe ^{3+}}$
$ 0 \cdot 712=(0+0 \cdot 771)-\frac{0 \cdot 06}{1} \log \frac{ Fe ^{2+}}{ Fe ^{3+}} $
$ \log \frac{ Fe ^{2+}}{ Fe ^{3+}}=\frac{0 \cdot 059}{0 \cdot 06} \approx 1 $
$ \frac{ Fe ^{2+}}{ Fe ^{3+}}=10$
Answer: 798
Solution
For one photon $E=h v$
For one mole photon,
$E =6 \cdot 023 \times 10^{23} \times 6 \cdot 626 \times 10^{-34} \times 2 \times 10^{12}$
$ =798 \cdot 16 J $
$ \approx 798\, J$
Answer: 186
Solution
Total milimoles of $ H ^{+} =(600 \times 0.01)+(400 \times 0.01 \times 2)$
$ =14 $
$ {\left[ H ^{+}\right] } =\frac{14}{1000}=14 \times 10^{-3} $
$ pH =3-\log 14 $
$ =1.86 $
$ =186 \times 10^{-2}$
Answer: 221
Solution
Molarity $=\frac{\text { mole }}{\text { volume }} $
$2.6 \times 10^{-3} =\frac{ x / 85}{0.67141} $
$x =0.148 \,g$
conc. Fo DCM in ppm $=\frac{0.148}{1.49 \times 671.141} \times 10^6 $
$ =148 \,ppm $
Answer: 623
Solution

at constant volume
$t =\frac{2.303}{ K } \log \frac{[ A ]_0}{[ A ]_{ t }}$
$ =\frac{2.303}{2 \cdot 011 \times 10^{-3}} \log \frac{7}{2} $
$=\frac{2 \cdot 303 \times 0 \cdot 544}{2 \cdot 011 \times 10^{-3}} $
$ =622.989 $
$ \approx 623$
Answer: 3
Solution
$\overset{+7}{Mn}O _4^{-}+4 H ^{+}+3 e ^{-} \rightarrow \overset{+4}{ Mn}O _2+2 H _2 O$
Answer: 1362
Solution
Mole of $CO _2=0.2 M \times\left(300 \times 10^{-3}\right) L$ $=0.06$ Mole
Volume of $0.06$ mole $CO _2$ at S.T.P
$ =0.06 \times 22.7$
$ =1.362 L$
JEE Main Mathematics Question Paper with Solution 2023 January 29th Shift 1 - Morning
A
$a=3 b$
B
$a=b$
C
$ab =1$
D
$a b=3$
Solution
Coefficient Of$ x^{15} \text { in }\left(a x^3+\frac{1}{b x^{1 / 3}}\right)^{15} $
$T_{r+1}={ }^{15} C_r\left(a x^3\right)^{15-r}\left(\frac{1}{b x^{1 / 3}}\right)^r$
$ 45-3 r-\frac{r}{3}=15$
$ 30=\frac{10 r}{3} $
$ r=9$
Coefficient of $x^{15}={ }^{15} C_9 a^6 b^{-9}$
Coefficient of $ x^{-15} \text { in }\left(a x^{1 / 3}-\frac{1}{b x^3}\right)^{15}$
$T _{ r +1}={ }^{15} C _{ r }\left( ax { }^{1 / 3}\right)^{15- r }\left(-\frac{1}{b x^3}\right)^{ r } $
$ 5-\frac{ r }{3}-3 r =-15$
$ \frac{10 r}{3}=20 $
$ r=6$
Coefficient $={ }^{15} C _6 a ^9 \times b ^{-6}$
$ \Rightarrow \frac{a^9}{b^6}=\frac{a^6}{b^9}$
$ \Rightarrow a^3 b^3=1 \Rightarrow a b=1 $
A
$\exp \left(\frac{4+\pi}{4 \sqrt{2}}\right)$
B
$\exp \left(\frac{4-\pi}{4 \sqrt{2}}\right)$
C
$\exp \left(\frac{1-\pi}{4 \sqrt{2}}\right)$
D
$\exp \left(\frac{\pi-4}{4 \sqrt{2}}\right)$
Solution
$ \frac{d y}{d x}+\left(\frac{-3 x^5 \tan ^{-1} x^3}{\left(1+x^6\right)^{3 / 2}}\right) y=2 e^{\left\{\frac{x-\tan x}{\left.\sqrt{1+x^6}\right\}}\right\}} $
$ \text { I.F. }=e^{\int \frac{-3 x^5 \tan ^{-1} x^3}{\left(1+x^6\right)^{32}} d x} $
$ =e^{\frac{\tan ^{-1} x^3-x^3}{\sqrt{1+x^6}}}$
Solution of differential equation
$y \cdot e^{\frac{\tan ^{-1} x^3-x^3}{\sqrt{1+x^6}}}=\int 2 x e^{\left(\frac{x^3-\tan ^{-1} x^3}{\sqrt{1+x^6}}\right)} \cdot e^{\left(\frac{\tan ^{-1}\left(x^3\right)-x^3}{\sqrt{1+x^6}}\right)} d x$
$ =\int 2 x d x+c$
$y \cdot e^{\frac{\tan ^{-1} x^3-x^3}{\sqrt{1+x^6}}}=x^2+c$
Also it passes through origin
$c =0$
$ y(1) \cdot e^{\frac{\tan ^{-1}(1)-1}{\sqrt{2}}}=1 $
$ y(1) \cdot e^{\frac{\frac{\pi}{4}-1}{\sqrt{2}}}=1 $
$y(1) \cdot e^{\frac{\pi-4}{4 \sqrt{2}}}=1$
$ y(1)=\frac{1}{e^{\frac{\pi-4}{4 \sqrt{2}}}}=e^{\frac{4-\pi}{4 \sqrt{2}}}$
A
2
B
4
C
0
D
3
Solution
Normal of line is parallel to line $x+90 y+2=0$
$m _{ N }=-\frac{1}{90} $
$ -\left(\frac{ dx }{ dy }\right)_{\left(x_1 y_1\right)}=-\frac{1}{90} \Rightarrow\left(\frac{ dy }{ dx }\right)_{\left(x_1 y_1\right)}=90$
Now,
$ \frac{d y}{d x}=270 x^4-540 x^3-210 x^2+360 x+210=90$
$ \Rightarrow x=1,2, \frac{-2}{3}, \frac{-1}{3}$
(4) normals
A
4
B
2
C
$4-2 \sqrt{3}$
D
$5-\frac{3}{2} \sqrt{3}$
Solution
$\tan 15^{\circ}=2-\sqrt{3}$
$ \frac{1}{\tan 75^{\circ}}=\cot 75^{\circ}=2-\sqrt{3} $
$ \frac{1}{\tan 105^{\circ}}=\cot \left(105^{\circ}\right)=-\cot 75^{\circ}=\sqrt{3}-2$
$ \tan 195^{\circ}=\tan 15^{\circ}=2-\sqrt{3}$
$ \therefore 2(2-\sqrt{3})=2 a \Rightarrow a=2-\sqrt{3} $
$\Rightarrow a+\frac{1}{a}=4$
A
$e^8-1$
B
$e^7-1$
C
$e^9-e$
D
$e^8-e$
Solution
$ \int\limits_1^2 x ^2 e ^{\left[ x ^3\right]+1} dx$
$ x ^3= t$
$ 3 x ^2 dx = dt $
$ =\frac{ e }{3} \int\limits_1^8 e ^{[ t ]} dt $
$=\frac{ e }{3}\left\{\int\limits_1^2 e dt +\int_2^3 e ^2 dt +\ldots \ldots . .+\int\limits_7^8 e ^7 dt \right\} $
$ =\frac{ e }{3}\left( e + e ^2+\ldots \ldots \ldots+ e ^7\right)$
$ =\frac{ e ^2}{3}\left(1+ e +\ldots \ldots \ldots+ e ^6\right)=\frac{ e ^2}{3} \frac{\left( e ^7-1\right)}{( e -1)}$
$ \frac{3( e -1)}{ e } \int\limits_1^2 x ^2 \times e ^{[ x ]+\left[ x ^3\right]} dx =\frac{3}{ e }( e -1) \times \frac{ e ^2}{3} \frac{\left( e ^7-1\right)}{( e -1)}$
$ = e \left( e ^7-1\right) $
$ = e ^8- e $
A
5
B
$5(1+\sqrt{2})$
C
6
D
$5 \sqrt{2}$
Solution
$L _1: y = x +2, L _2: 4 y =3 x +6, L _3: 3 y =4 x +1$
Bisector of lines $L _2 \& L _3$
$ \frac{4 x-3 y+1}{5}=\pm\left(\frac{3 x-4 y+6}{5}\right)$
$(+) 4 x-3 y+1=3 x-4 y+6$
$ x+y=5$
Centre lies on Bisector of $4 x-3 y+1=0 \&$
(0) $3 x-4 y+6=0$
$\Rightarrow h + k =5$
A
6
B
4
C
5
D
3
Solution
$ \log _{\cos x} \cot x+4 \log _{\sin x} \tan x=1$
$ \Rightarrow \frac{\ln \cos x-\ln \sin x}{\ln \cos x}+4 \frac{\ln \sin x-\ln \cos x}{\ln \sin x}=1$
$ \Rightarrow(\ln \sin x)^2-4(\ln \sin x)(\ln \cos x)+4(\ln \cos x)^2=1 $
$ \Rightarrow \ln \sin x=2 \ln \cos x $
$ \Rightarrow \sin ^2 x+\sin x-1=0 \Rightarrow \sin x=\frac{-1+\sqrt{5}}{2} $
$ \therefore \alpha+\beta=4$
Correct option (4)
A
$\frac{440}{2592}$
B
$\frac{881}{2592}$
C
$\frac{27}{288}$
D
$\frac{521}{2592}$
Solution
Either all outcomes are positive or any two are negative.
$ \text { Now, } p = P (\text { positive })=\frac{3}{6}=\frac{1}{2} $
$q = p (\text { negative })=\frac{2}{6}=\frac{1}{3}$
Required probability
$={ }^5 C_5\left(\frac{1}{2}\right)^5+{ }^5 C_2\left(\frac{1}{3}\right)^2\left(\frac{1}{2}\right)^3+{ }^5 C_4\left(\frac{1}{3}\right)^4\left(\frac{1}{2}\right)^1 $
$ =\frac{521}{2592}$
A
${ }^{500} C _{301}$
B
${ }^{501} C_{200}$
C
${ }_3{ }^{500} C_{300}$
D
${ }^{501} C_{302}$
Solution
$ (1+x)^{500}+x(1+x)^{499}+x^2(1+x)^{498}+\ldots+x^{500} $
$ =(1+x)^{500} \cdot\left\{\frac{1-\left(\frac{x}{1+x}\right)^{501}}{1-\frac{x}{1+x}}\right\}$
$=(1+x)^{500} \frac{\left((1+x)^{501}-x^{501}\right)}{(1+x)^{501}} \cdot(1+x) $
$=(1+x)^{501}-x^{501}$
Coefficient of $x^{301}$ in $(1+x)^{501}-x^{501}$ is given by
${ }^{501} C_{301}={ }^{501} C_{200}$
A
$\frac{52}{147}$
B
$\frac{50}{141}$
C
$\frac{51}{144}$
D
$\frac{49}{138}$
Solution
If $a_n=\frac{-2}{4 n^2-16 n+15}$ then $a_1+a_2+\ldots \ldots \ldots a_{25}$
$\Rightarrow \displaystyle\sum_{n=1}^{25} a _{ n }=\sum \frac{-2}{4 n ^2-16 n +15} $
$=\sum \frac{-2}{4 n^2-6 n-10 n +15} $
$=\sum \frac{-2}{2 n (2 n -3)-5(2 n -3)} $
$=\sum \frac{-2}{(2 n-3)(2 n-5)}$
$ =\sum \frac{1}{2 n-3}-\frac{1}{2 n-5} $
$=\frac{1}{47}-\frac{1}{(-3)} $
$ =\frac{50}{141}$
A
3
B
7
C
4
D
5
Solution
For Symmetric $(a, b),(b, c) \in R$
$\Rightarrow(b, a),(c, b) \in R$
For Transitive $(a, b),(b, c) \in R$ $\Rightarrow(a, c) \in R$
Now
1. Symmetric
$\therefore(a, c) \in R \Rightarrow(c, a) \in R$
2. Transitive
$\therefore(a, b),(b, a) \in R $
$ \Rightarrow(a, a) \in R \&(b, c),(c, b) \in R$
$ \Rightarrow(b, b) \&(c, c) \in R$
$\therefore$ Elements to be added
$\left\{ (b, a),(c, b),(a, c),(c, a) ,(a, a),(b, b),(c, c) \right\}$
Number of elements to be added $=7$
A
4
B
2
C
8
D
6
Solution
Equation of normal
$ y=-t x+2 a t+a t^3 $
$ y=-t x+\frac{2}{16} t+\frac{1}{16} t^3$
It passes through $(0,33)$
$ 33=\frac{t}{8}+\frac{t^3}{16}$
$ t ^3+2 t -528=0$
$ ( t -8)\left( t ^2+8 t +66\right)=0 $
$ t =8$
$ P \left( at { }^2, 2 at \right)=\left(\frac{1}{16} \times 64,2 \times \frac{1}{16} \times 8\right)=(4,1)$
Parabola :
$ y^2=4(x+y)$
$ \Rightarrow y^2-4 y=4 x $
$ \Rightarrow(y-2)^2=4(x+1)$
Equation of directix :-
$x+1=-1 $
$ x=-2$
Distance of point $=6$
Ans. : (4)
A
infinitely many solutions
B
unique solution satisfying $x-y=1$
C
no solution
D
unique solution satisfying $x+y=1$
Solution
$\begin{vmatrix} 1 & 1 & k \\ 2 & 3 & -1 \\ 3 & 4 & 2 \end{vmatrix}=0 $
$ \Rightarrow 1(10)-1(7)+ k (-1)-0$
$ \Rightarrow k =3$
For $k =3,2^{ md }$ system is
$4 x +5 y =7 ....$(1)
and $7 x+8 y=10....$(2)
Clearly, they have a unique solution
(2) $-(1) \Rightarrow 3 x +3 y =3$
$\Rightarrow x+y=1$
A
$\frac{19}{3}$
B
7
C
9
D
$\frac{13}{3}$
Solution
Line $\ell$, is given by
$L _1: \frac{ x -2}{2}=\frac{ y -6}{1}=\frac{ z -2}{-2}$
Given,
$L _2: \frac{ x +1}{2}=\frac{ y +4}{-3}=\frac{ z }{2}$

Shortest distance $=\left|\frac{\overrightarrow{ AB } \cdot \overrightarrow{ MN }}{ MN }\right|$
$ \overrightarrow{ AB }=3 \hat{ i }+10 \hat{ j }+2 \hat{ k } $
$\overrightarrow{ MN }= \begin{vmatrix} \hat{ i } & \hat{ j } & \hat{ k } \\2 & 1 & -2 \\2 & -3 & 2\end{vmatrix}=-4 \hat{ i }-8 \hat{ j }-8 \hat{ k } $
$MN =\sqrt{16+64+64}=12$
$\therefore$ Shortest distance $=\left|\frac{-12-80-16}{12}\right|=9$
$\therefore$ Option (4) is correct.
A
9
B
15
C
6
D
12
Solution
$ \hat{ n } \perp \vec{ c } \,\,\, \vec{ a }=\alpha \vec{ b }-\vec{ n } $
$ \vec{b} \cdot \vec{c}=12$
$ \vec{ a } \cdot \vec{ c }=\alpha(\vec{ b } \cdot \vec{ c })-\vec{ n } \cdot \vec{ c } $
$ \vec{a} \cdot \vec{c}=\alpha(\vec{b} \cdot \vec{c}) $
$ |\vec{c} \times(\vec{a} \times \vec{b})|=|(\vec{c} \cdot \vec{b}) \vec{a}-(\vec{c} \cdot \vec{a}) \vec{b}|$
$ =|(\vec{ c } \cdot \vec{ b }) \vec{ a }-\alpha(\vec{ b } \cdot \vec{ c }) \vec{ b }| $
$ =|(\vec{c} \cdot \vec{b})||\vec{ a }-\alpha \vec{ b }| $
$ =12 \times(|\vec{ n }|) $
$ =12 \times 1 $
$ =12 $
A
only (S2) is a tautology
B
both (S1) and (S2) are tautologies
C
only (S1) is a tautology
D
neither (S1) nor (S2) is a tautology
Solution

$S_2 \equiv(p \vee q) \Rightarrow r \Leftrightarrow((p \Rightarrow r) \vee(q \Rightarrow r))$

A
$\alpha \in\left(0, \frac{\pi}{2}\right)$ and $\gamma \in\left(0, \frac{\pi}{2}\right)$
B
$\alpha \in\left(\frac{\pi}{2}, \pi\right)$ and $\gamma \in\left(\frac{\pi}{2}, \pi\right)$
C
$\alpha \in\left(\frac{\pi}{2}, \pi\right)$ and $\gamma \in\left(0, \frac{\pi}{2}\right)$
D
$\alpha \in\left(0, \frac{\pi}{2}\right)$ annd $\gamma \in\left(\frac{\pi}{2}, \pi\right)$
Solution
Equation of plane :-
$ \begin{vmatrix} x-1 & y-2 & z-3 \\ 1 & 1 & 1 \\ 0 & 3 & 4 \end{vmatrix}=0 $
$ \Rightarrow[x-1]-4[y-2]+3[z-3]=0$
$ \Rightarrow x-4 y+3 z=2$
D.R's of normal of plane $<1,-4,3>$
D.C's of
$\left\langle\pm \frac{1}{\sqrt{26}}, \mp \frac{4}{\sqrt{26}}, \pm \frac{3}{\sqrt{26}}\right\rangle$
$ \cos \beta=\frac{4}{\sqrt{26}} $
$\cos \alpha=\frac{-1}{\sqrt{26}} \frac{\pi}{2} < \alpha < \pi $
$\cos \gamma=\frac{-3}{\sqrt{26}} \frac{\pi}{2} < \gamma < \pi$
A
$\frac{392}{3}$
B
$\frac{196}{3}$
C
196
D
98
Solution

Equation of straight line : $\frac{ x }{ a }+\frac{ y }{ b }=1$
Or $x \cos \frac{\pi}{3}+y \sin \frac{\pi}{3}=p$
$\frac{x}{2}+\frac{y \sqrt{3}}{2}=p$
$\frac{x}{3 p}+\frac{y}{2 p}=1$
Comparing both : $a=2 p , b =\frac{2 p }{\sqrt{3}}$
Now area of $\triangle OAB =\frac{1}{2} \cdot ab =\frac{98}{3} \cdot \sqrt{3}$
$\frac{1}{2} \cdot 2 p \cdot \frac{2 p }{\sqrt{3}}=\frac{98}{3} \cdot \sqrt{3}$
$p ^2=49$
$a^2-b^2=4 p^2-\frac{4 p^2}{3}=\frac{2}{3} 4 p^2$
$=\frac{8}{3} \cdot 49=\frac{392}{3}$
A
$1+d^2=m^2+q^2$
B
$1+d^2=(m+q)^2$
C
$(1+d)^2=m^2+q^2$
D
$(1+d)^2=(m+q)^2$
Solution
$ A =\begin{bmatrix} m & n \\ p & q \end{bmatrix}, | A - d (\operatorname{adj} A )|=0 $
$ \Rightarrow | A - d (\operatorname{adj} A )|=\left|\begin{bmatrix} m & n \\ p & q \end{bmatrix}- d \begin{bmatrix} q & - n \\ - p & m \end{bmatrix}\right| $
$ =\begin{vmatrix} m - qd & n (1+ d ) \\ p (1+ d ) & q - md \end{vmatrix}=0 $
$\Rightarrow ( m - qd )( q - md )- np (1+ d )^2=0 $
$ \Rightarrow mq - m ^2 d - q ^2 d + mqd d ^2- np (1+ d )^2=0$
$\Rightarrow ( mq - np )+ d ^2( mq - np )- d \left( m ^2+ q ^2+2 np \right)=0 $
$ \Rightarrow d + d ^3- d \left(( m + q )^2-2 d \right)=0$
$ \Rightarrow 1+ d ^2=( m + q )^2-2 d$
$\Rightarrow (1+ d )^2=( m + q )^2$
$ \therefore Option (1) $ is correct.
A
6575
B
6825
C
6875
D
6525
Solution
$ 5 f ( x + y )= f ( x ) \cdot f ( y ) $
$ 5 f (0)= f (0)^2 \Rightarrow f (0)=5$
$5 f ( x +1)= f ( x ) \cdot f (1) $
$\Rightarrow \frac{ f ( x +1)}{ f ( x )}=\frac{ f (1)}{5} $
$\Rightarrow \frac{ f (1)}{ f (0)} \cdot \frac{ f (2)}{ f (1)} \cdot \frac{ f (3)}{ f (2)}=\left(\frac{ f (1)}{5}\right)^3$
$\Rightarrow \frac{320}{5}=\frac{( f (1))^3}{5^3} \Rightarrow f (1)=20$
$\therefore 5 f ( x +1)=20 \cdot f ( x ) \Rightarrow f ( x +1)=4 f ( x )$
$\displaystyle\sum_{ n =0}^5 f ( n )=5+5.4+5.4^2+5.4^3+5.4^4+5.4^5$
$=\frac{5\left[4^6-1\right]}{3}=6825$
Answer: 12
Solution
$48 \displaystyle\lim _{x \rightarrow 0} \frac{\int\limits_0^x \frac{t^3}{t^6+1} d t}{x^4}\left(\frac{0}{0}\right)$
Applying L' Hospitals Rule
$ 48 \displaystyle\lim _{x \rightarrow 0} \frac{x^3}{x^6+1} \times \frac{1}{4 x^3} $
$= 12$
Answer: 22
Solution

$y=x$
& $y^2=8 x$
Solving it
$ x^2=8 x $
$ \therefore x=0,8$
$ \therefore y=0,8 $
$ x=2 \text { will intersect occur at } $
$ y^2=16 \Rightarrow y=\pm 4 $
$ \therefore \text { Area of shaded }$
$ =\int\limits_2^8(\sqrt{8 x}-x) d x=\int\limits_2^8(2 \sqrt{2} \sqrt{x}-x) d x $
$=\left[2 \sqrt{2} \cdot \frac{x^{3 / 2}}{3 / 2}-\frac{x^2}{2}\right]_0^8$
$ =\left(\frac{4 \sqrt{2}}{3} \cdot 2^{9 / 2}-32\right)-\left(\frac{4 \sqrt{2}}{3} \cdot 2^{9 / 2}-2\right) $
$ =\frac{128}{3}-32-\frac{16}{3}+2=\frac{112-90}{3}=\frac{22}{3}= A$
$ \therefore 3 A =22 $
Answer: 26
Solution
$ \displaystyle\sum_{n=0}^{\infty} \frac{n^3((2 n) !)+(2 n-1)(n !)}{(n !)((2 n) !)} $
$=\displaystyle\sum_{n=0}^{\infty} \frac{1}{(n-3) !}+\displaystyle\sum_{n=0}^{\infty} \frac{3}{(n-2) !} +\sum_{n=0}^{\infty} \frac{1}{(n-1) !}+\displaystyle\sum_{n=0}^{\infty} \frac{1}{(2 n-1) !}-\displaystyle\sum_{n=0}^{\infty} \frac{1}{(2 n) !} $
$ =e+3 e+e+\frac{1}{2}\left(e-\frac{1}{e}\right)-\frac{1}{2}\left(e+\frac{1}{e}\right)$
$ =5 e-\frac{1}{e} $
$ \therefore a^2-b+c=26$
Answer: 21
Solution
For number to be divisible by 15, last digit should be 5 and sum of digits must be divisible by 3.

Answer: 3240
Solution
Let $S=\{1,2,3,4,5,6\}$, then the number of one-one functions, $f : S \cdot P ( S )$, where $P ( S )$ denotes the power set of $S$, such that $f(n)< f(m)$ where $n< m$ is
$n(S)=6$
$P(S)=\begin{Bmatrix}\phi,\{1\}, \ldots\{6\},\{1,2\}, \ldots, \\\{5,6\}, \ldots,\{1,2,3,4,5,6\}\end{Bmatrix}$
$-64$ elements
case $-1$
$f(6)=S$ i.e. 1 option,
$f (5)=$ any 5 element subset $A$ of $S$ i.e. 6 options,
$f (4)=$ any 4 element subset $B$ of $A$ i.e. 5 options,
$f(3)=$ any 3 element subset $C$ of $B$ i.e. 4 options,
$f (2)=$ any 2 element subset $D$ of $C$ i.e. 3 options,
$f(1)=$ any 1 element subset $E$ of $D$ or empty subset i.e. 3
options,
Total functions $=1080$
Case $-2$
$f(6)=$ any 5 element subset $A$ of $S$ i.e. 6 options,
$f(5)=$ any 4 element subset $B$ of $A$ i.e. 5 options,
$f^{\prime}(4)=$ any 3 element subset $C$ of B i.e. 4 options,
$f (3)=$ any 2 element subset $D$ of $C$ i.e. 3 options,
$f^{\prime}(2)=$ any 1 element subset $E$ of $D$ i.e. 2 options,
$f(1)=$ empty subset i.e. 1 option
Total functions $=720$
Case $-3$
$f(6)=S$
$f(5)=$ any 4 element subset $A$ of ' $S$ i.e. 15 options,
$f(4)=$ any 3 element subset $B$ of $A$ i.e. 4 options,
$f(3)=$ any 2 element subset $C$ of $B$ i.e. 3 options,
$f(2)=$ any 1 element subset $D$ of $C$ i.e. 2 options,
$f(1)=$ empty subset i.e. 1 option
Total functions $=360$
Case $-4$
$f(6)=S$
$f(5)=$ any 5 element subset $A$ of $S$ i.e. 6 options,
$f(4)=$ any 3 element subset $B$ of $A$ i.e. 10 options,
$f(3)=$ any 2 element subset $C$ of $B$ i.e. 3 options,
$f(2)=$ any 1 element subset $D$ of $C$ i.e. 2 options,
$f(1)=$ empty subset i.e. 1 option
Total functions $=360$
Case $-5$
$f(6)=S$
$f(5)=$ any 5 element subset $A$ of $S$ i.e. 6 options,
$f(4)=$ any 4 element subset $B$ of $A$ i.e. 5 options,
$f(3)=$ any 2 element subset $C$ of $B$ i.e. 6 options,
$f(2)=$ any 1 element subset $D$ of $C$ i.e. 2 options,
$f(1)=$ empty subset i.e. 1 option
Total functions $=360$
Case $-6$
$f(6)=S$
$f(5)=$ any 5 element suhset $A$ of $S$ i e 6 options
$f(4)=$ any 4 element subset $B$ of $A$ i.e. 5 options,
$f(3)=$ any 3 element subset $C$ of $B$ i.e. 4 options,
$f(2)=$ any 1 element subset $D$ of $C$ i.e. 3 options,
$f(1)=$ empty subset i.e. 1 option
Total functions $=360$
$\therefore$ Number of surch funstions $=3240$
Answer: 15
Solution
$ x-3 y+2 z-1=0 $
$ 4 x-y+z=0$
$\overrightarrow{ n }_1 \times \overrightarrow{ n }_2=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 1 & -3 & 2 \\ 4 & -1 & 1\end{vmatrix}$
$=-\hat{ i }+7 \hat{ j }+11 \hat{ k }$
Dr of normal to the plane is $-1,7,11$
Equation of plane :
$ -1(x-1)+7(y-1)+11(z-2)=0$
$ -x+7 y+11 z=28$
$ \frac{-1}{28} x+\frac{7 y}{28}+\frac{11 z}{28}=1$
$ Ax + By + Cz =1 $
$140( C - B + A )=140\left(\frac{11}{28}-\frac{7}{28}-\frac{1}{28}\right)$
$ =140 \times \frac{3}{28}=15$
Answer: 37
Solution
$ \frac{x_1+x_2+\ldots+x_7}{7}=8 $
$ \frac{x_1+x_2+x_3 \ldots+x_6+14}{7}=8 $
$ \Rightarrow x_1+x_2+\ldots .+x_6=42 $
$ \therefore \frac{ x _1+ x _2 \ldots .+ x _6}{6}=\frac{42}{6}=7= a $
$\frac{\Sigma x _{ i }^2}{7}-8^2=16 $
$ \Sigma xi ^2=560 $
$ \Rightarrow x_1^2+x_2^2+\ldots+x_6^2=364 $
$ b =\frac{ x _1^2+ x _2^2+\ldots .+ x _6^2}{6}-7^2 $
$ =\frac{364}{6}-49 $
$ b =\frac{70}{6} $
$a+3 b-5=7+3 \times \frac{70}{6}-5 $
$ =37$
Answer: 315
Solution
$ P_1=\vec{ r } \cdot(3 \hat{ i }-5 \hat{ j }+\hat{ k })=7$
$ P _2=\vec{ r } \cdot(\lambda \hat{ i }+\hat{ j }-3 \hat{ k })=9$
$\theta=\sin ^{-1}\left(\frac{2 \sqrt{6}}{5}\right) $
$ \Rightarrow \sin \theta=\frac{2 \sqrt{6}}{5} $
$ \therefore \cos \theta=\frac{1}{5} . $
$\cos \theta=\frac{\overrightarrow{ r } \cdot \overrightarrow{ r }}{|\overrightarrow{ r }|\left|\overrightarrow{ r _2}\right|}$
$ =\frac{(3 i-5 j+K)(\lambda i+j-3 K)}{\sqrt{35} \cdot \sqrt{\lambda^2+10}} $
$ \frac{1}{5}=\left|\frac{3 \lambda-8}{\sqrt{35} \cdot \sqrt{\lambda^2+10}}\right| $
$ \text { Square } \Rightarrow \frac{1}{25}=\frac{9 \lambda^2+64-48 \lambda}{35\left(\lambda^2+10\right)}$
$ \Rightarrow 19 \lambda^2-120 \lambda+125=0 $
$ \Rightarrow 19 \lambda^2-95 \lambda-25 \lambda+125=0$
$ \Rightarrow x=5, \frac{25}{19}$

Perpendicular distance of point
$\left(38 \lambda_1, 10 \lambda_2, 2\right)=(50,50,2)$ from plane $P_1$
$=\frac{|3 \times 50-5 \times 50+2-7|}{\sqrt{35}}=\frac{105}{\sqrt{35}}$
Square $=\frac{105 \times 105}{35}=315$
Answer: 9
Solution
$ z-1+i $
$ z_1=\frac{1+i \bar{z}}{\bar{z}(1-z)+\frac{1}{z}}$
$ z_1=\frac{1+i(1 \quad i)}{(1-i)(1-1-i)+\frac{1}{1+i}} $
$=\frac{1+i-i^2}{(1-i)(-i)+\frac{1-i}{2}} $
$=\frac{2+i}{-3 i-1}=\frac{4+2 i}{-3 i-1}$
$ =\frac{-(4+2 i)(3 i-1)}{(3 i)^2-(1)^2} $
$\text{Arg}\left(z_1\right)=\frac{3 \pi}{4}$
$\therefore \frac{12}{\pi} \arg \left( z _1\right)=\frac{12}{\pi} \times \frac{3 \pi}{4}=9$
Answer: 3125