JEE Main Question Paper with Solution 2022 July 28th Shift 1 - Morning

A

$\left[ M L ^2 T ^{-2}\right]$

B

$\left[ M L T ^{-2}\right]$

C

$\left[ M L ^{-1} T ^{-2}\right]$

D

$\left[ M L ^2 T ^{-2} A ^{-1}\right]$

Solution

$ u =\frac{ B ^2}{2 \mu_0} $
$ u \rightarrow $ Energy per unit volume
$ {\left[\frac{ B ^2}{\mu_0}\right]=[ u ]=\frac{\left[ ML ^2 T ^{-2}\right]}{\left[ L ^3\right]}=\left[ ML ^{-1} T ^{-2}\right]}$

A

$5 \,m$

B

$10 \,m$

C

$19.8\, m$

D

$24.5 \,m$

Solution

Time taken by mango $=\sqrt{\frac{2 n }{ g }} $
$ =\sqrt{\frac{2 \times 19.6}{9.8}}=2 $ second
Distance $= vt $
$ =9 \times \frac{5}{18} \times 2=5\, m $

A

Impulse and average force acting on the object will be same for both the cases.

B

Impulse will be same for both the cases but the average force will be different.

C

Average force will be same for both the cases but the impulse will be different.

D

Average force and impulse will be different for both the cases.

Solution

Impulse $=$ change in momentum
$I =\Delta P$
$ F _{\text {aug }}=\frac{\Delta P }{\Delta t } $
$ \Delta t _1=3 \,\,\, \Delta t _2=5$
$ \Delta P _1=\Delta P _2 $
$ I _1= I _2$
$F _{\text {avg }}$ in case (i) is more than (ii)

A

3

B

9

C

12

D

18

Solution

$ F =\frac{ dm }{ dt } v $
$ =\frac{10 g }{5 s }\left(4.5 \frac{ cm }{ s }\right)=9 \frac{ gcm }{ s ^2}=9 $ dyne

A

decrease by $2 \%$

B

decrease by $4 \%$ $

C

$ increase by $2 \%$

D

increase by $4 \%$

Solution

$ g =\frac{ GM }{ R ^2} $
$ M =\text { constant } g <\frac{1}{ R ^2} $
$ 100 \frac{\Delta g }{ g }=-2 \frac{\Delta R }{ R } 100$
$\%$ change $=-2(-2)$
$\%$ change in $g =4 \%$
increase by $4 \%$

A

$1 \times 10^7 N$

B

$1.5 \times 10^7 N$

C

$2 \times 10^7 N$

D

$2.5 \times 10^7 N$

Solution

$ F =\gamma A \frac{\Delta \ell}{\ell} $
$ =2 \times 10^{11} \times 10^{-4}\left(\frac{2 \ell-\ell}{\ell}\right) $
$ =2 \times 10^7 N $

A

$166.7 \,K$

B

$255.1 \,K$

C

$266.7\, K$

D

$367.7 \,K$

Solution

$ \eta=1-\frac{ T _{ L }}{ T _{ H }} $
$ \frac{1}{2}=1-\frac{ T _{ L }}{ T _{ H }} $
$ \frac{1}{2}(1 \cdot 3)=1-\left(\frac{ T _{ L }-40}{ T _{ H }}\right) $
$ \frac{1}{2}(1 \cdot 3)=\frac{1}{2}+\frac{40}{ T _{ H }}$
$ T _{ H }=266.7 \,K $

A

Both Statement I and Statement II are true

B

Both Statement I and Statement II are false

C

Statement I is true but Statement II is false

D

Statement I is false but Statement II is true

Solution

$ {\left[ P _{ avg }=0\right]} $ (due to random motion)
$ v _{ rms }=\sqrt{\frac{3 RT }{ M }} $
$ T _\text{ new }=2 T$
$ M _{\text {new }}=\frac{ M }{2} $
$ \frac{ v _{\text {new }}}{ v }=\frac{\sqrt{\frac{2 T }{ M / 2}}}{\sqrt{\frac{ T }{ M }}}$

A

$200 m / s$

B

$200 \sqrt{2} m / s$

C

$400 m / s$

D

$400 \sqrt{2} m / s$

Solution

$ y =0.5 \sin \left(\frac{2 \pi}{\lambda} 400 t -\frac{2 \pi}{\lambda} x \right)$
$\omega=\frac{2 \pi}{\lambda} 400 $
$ K =\frac{2 \pi}{\lambda} $
$v =\frac{\omega}{ k } [ v =400 m / s ]$

A

$1.5$

B

$2.5$

C

$1.2$

D

3

Solution

$ C _{ eq }=\frac{ C ( KC )}{ C + KC }=\frac{ KC }{ K +1} $
$ 24=\frac{ K 40}{ K +1} $
$ {[ K =1 \cdot 5]}$

A

$9: 1$

B

$1: 9$

C

$4: 1$

D

$3: 1$

Solution

$ R _1=\rho \frac{ L _1}{ A _1} $
$R _2=\rho\left(\frac{3 L _1}{ A _1 / 3}\right)=9 \rho \frac{ L _1}{ A _1} $
$\therefore \frac{ R _2}{ R _1}=9$

A

(B) and (C) only

B

(C) and (D) only

C

(A) and (C) only

D

(B) and (D) only

Solution

$ i =\left(\frac{ K }{ NAB }\right) \theta $
$ \therefore \frac{ d \theta}{ di }=\frac{ NAB }{ K }$

A

$30 \,A$

B

$15\, A$

C

$10\, A$

D

$3 \,A$

Solution

$mg \sin 45^{\circ}= ILB \cos 45^{\circ}$
$ \therefore I =\left(\frac{ m }{ L }\right) \frac{ g }{ B }$
$ =\frac{(0.45)(10)}{0.15}=30 A$

A

$1.47 \sin \left(49 \pi t -30^{\circ}\right)$

B

$1.47 \sin \left(49 \pi t +60^{\circ}\right)$

C

$23.1 \sin \left(49 \pi t -30^{\circ}\right)$

D

$23.1 \sin \left(49 \pi t+60^{\circ}\right)$

Solution

$v_0=i_0 x_L $
$=i_0(w L)$
$=(5)(49 \pi)\left(30 \times 10^{-3}\right)$
$ =23.1$
Voltage will lead current by $90^{\circ}$.
$\therefore V =23.1 \sin \left(49 \pi t +60^{\circ}\right)$

A

$1.0 \times 10^8 \,ms ^{-1}$

B

$0.5 \times 10^8 \, ms ^{-1}$

C

$1.5 \times 10^8 \,ms ^{-1}$

D

$3.0 \times 10^8 \, ms ^{-1}$

Solution

$ \frac{\mu_2}{\mu_{\text {air }}}=\frac{ C }{ v _2} $
$ \therefore \frac{\sqrt{\mu_{ r _2} \varepsilon_{ r _2}}}{(1)}=\frac{ C }{ v _2} $
$ \therefore \sqrt{(1)(9)}=\frac{ C }{ v _2} $
$ \therefore v _2=\frac{ C }{3}$

A

$20\, cm$

B

$30 \,cm$

C

$10\, cm$

D

$15 \,cm$

Solution

$f _0+ f _{ e }=30 $
$m =\frac{ f _0}{ f _{ e }} $
$ 2=\frac{ f _0}{ f _{ e }} \Rightarrow f _0=2 f _{ e }$
So $f _0+\frac{ f _0}{2}=30$
$f _0=20\, cm$

A

$\sqrt{m K}$

B

$\sqrt{ P }$

C

$\sqrt{ K }$

D

$\sqrt{ V }$

Solution

$ \left.\lambda=\frac{ h }{ m v} \text { (de-Broglie's wavelength }\right)$
$ \lambda \frac{ h }{\sqrt{2 m ( K \cdot E )}}$
$ h =\frac{ h }{\sqrt{2 mqV }}$
Putting the values of $m ; q$
We get $\lambda=\frac{1.22}{\sqrt{ V }} nm$

A

120 days

B

130 days

C

180 days

D

20 days

Solution

$7 / 8$ disintegrates means $1 / 8$ remains
Or $\left(\frac{1}{2}\right)^3 $
$ \therefore 3$ half lives
$ =180 $ days

A

120 days

B

130 days

C

180 days

D

20 days

Solution

$7 / 8$ disintegrates means $1 / 8$ remains
Or $\left(\frac{1}{2}\right)^3 $
$ \therefore 3$ half lives
$ =180 $ days

A

$\mu \leq 1$

B

$\mu \geq 1$

C

$\mu=2$

D

$\mu=0$

Solution

$ \mu=\frac{ A _{ m }}{ A _{ c }}$
$\mu \leq 1 $ to avoid distortion
because $\mu >1$ will result in interference between career frequency & message frequency.

Solution

$ \overrightarrow{ a } \cdot \overrightarrow{ b }=0 $
$ \therefore \overrightarrow{ a } \cdot \overrightarrow{ b }=0$
$ \therefore 2 \times 1+4 \times 2-2 \times \alpha=0 $
$ \therefore \alpha=5$

Solution

$A = A _0 \times 2^{- t / T } $
$\frac{ A _0}{64}= A _0 \times 2^{- t / T } $
$ \therefore t =6 T =6 \times 2 \cdot 5=15$ hours

Solution

$ \beta \propto \lambda$
$ \lambda_2=\frac{9}{8} \lambda_1 $
$ \therefore \beta_2=\frac{9}{8} \beta_1=\frac{9}{8} \times 560=630 \,nm $

Solution

Band width $=232-212=\frac{ R }{ L } $
$ \therefore L =\frac{5}{20}=250 \,mH $

Solution

$ E =\frac{ AC }{ AB }\left(V_{ A }- V _{ B }\right)$
$ \therefore 20 \times 10^{-3}=\frac{60}{300} \times \frac{4 \times 20}{ R +20}$
$ \therefore R =780 \Lambda$

Solution

$ |\tau|_{\max }= PE $
$\frac{\tau_1}{\tau_2}=\frac{ P _1 E _1}{ P _2 E _2}=\frac{1.2 \times 10^{-30} \times 5 \times 10^4}{2 \cdot 4 \times 10^{-30} \times 15 \times 10^4}=\frac{1}{6}$
Hence $x=6$

Solution

The hill will be a secondary source.

$f _1=$ frequency of the car w.r.t. the hill $f_1=\left(\frac{v}{v-v_s}\right) f=\left(\frac{330}{320}\right) \times 320=330 Hz$
$f _2=$ Frequency of the sound reflected by hill w.r.t. the car (echo)
$f _2=\left(\frac{ v + v _0}{ v }\right) f _1=\frac{(330+10)}{330} \times 330=340\, Hz$

Solution

As the bubble is rising steadily the net force acting on it will be zero

(Because of density of air the value of mg can be neglected)
So $B=F \Rightarrow \frac{4 \pi}{3} R^3 \rho g=6 \pi \eta R v$
Putting $R =1 \,mm =10^{-3} m$
$\rho=1.75 \times 10^3\, kg / m ^3 $
$g =10 \,m / s ^2$
$v =0.35 \times 10^{-2}\, m / s $
$\eta=\frac{10}{9} \simeq 1 \cdot 11 \text { SI unit }=11 \text { poise }( CGS )$

Solution

Using work - energy theorem
$ W _\text{ net }=\left( K _{ f }- K _{ i }\right)$
$ \Rightarrow-\frac{1}{2} Kx ^2=\frac{1}{2} m \left(\frac{ v }{2}\right)^2-\frac{1}{2} mv ^2=\frac{ E }{4}- E$
$ \Rightarrow \frac{1}{2} Kx ^2=\frac{3 E }{4} \Rightarrow K =\frac{3 E }{2 x ^2} $
$\Rightarrow K =\frac{3 E }{2 \times\left(\frac{1}{4}\right)^2}=24 E $
$ n =24$

Solution

$ I_1=I_3=\frac{M^2}{4} $
$ I_2=\frac{M R^2}{4}+M R^2=\frac{5}{4} M R^2=I_4$

So $I = I _1+ I _2+ I _3+ I _4$
$ =\frac{ MR ^2}{2}+\frac{5}{2} MR ^2 $
$ =3 MR ^2, \text { Putting R }=\frac{ a }{2} $
$ I =\frac{3 Ma ^2}{4}, \text { So } x =3$

A

A circular path around the nucleus in which an electron moves is proposed as Bohr's orbit.

B

An orbital is the one electron wave function $(\Psi)$ in an atom.

C

The existence of Bohr's orbits is supported by hydrogen spectrum.

D

Atomic orbital is characterised by the quantum numbers $n$ and $l$ only

Solution

Atomic orbital is characterised by $n , l, m$.

A

$\Delta H =\Delta U - P \Delta V$

B

$\Delta U = q + W$

C

$\Delta S_{\text {sys }}+\Delta S_{\text {surr }} \geq 0$

D

$\Delta G =\Delta H - T \Delta S$

Solution

If $U + Pv$ (By definition)
$\Delta 14=\Delta U +\Delta(\text{Pr})$ at constant pressure
$\Delta H =\Delta U + P \Delta V$

A

(A) - (I), (B) - (II), (C) - (III), (D) - (IV)

B

(A) - (IV), (B) - (I), (C) - (II), (D) - (III)

C

(A) - (II), (B) - (I), (C) - (IV), (D) - (III)

D

(A) - (II), (B) - (I), (C) - (III), (D) - (IV)

Solution

(a) $Cd ( s )+2 Ni ( OH )_3( s ) \rightarrow CdO ( s )+$
$2 Ni ( OH )_2( s )+ H _2 O ( l )$
Discharge of secondary Battery
(b) $Zn ( Hg )+ HgO$ (s) $\rightarrow ZnO ( s )+ Hg (l)$
(Primary Battery Mercury cell)
(c) $2 PbSO _4( s )+2 H _2 O (l) \rightarrow Pb ( s )+ PbO _2( s )$ $+2 H _2 SO _4( aq )$
Charging of secondary Battery
(d) $2 H _2( g )+ O _2( g ) \rightarrow 2 H _2 O (l)-$ Fuel cell

A

(A) - (II), (B) - (III), (C) - (I), (D) - (IV)

B

(A) - (III), (B) - (II), (C) - (I), (D) - (IV)

C

(A) - (III), (B) - (IV), (C) - (II), (D) - (I)

D

(A) - (III), (B) - (II), (C) - (IV), (D) - (I)

Solution

(a)$4 NH _3( g )+5 O _2( g ) \xrightarrow{ Pt ( s )} 4 NO ( g )+6 H _2 O ( g )$
Ostwald process $500 K$
(b) $N _2+3 H _2 \xrightarrow{ Fe ( s )} 2 NH _3( g )$
Haber's process
(c)
$C _{12} H _{22} O _{11} \text { (aq.) }+ H _2 O (\ell) \xrightarrow{ H ^{+}} \underset{\text { (glucose) }}{ C _6 H _{12} O _6}+\underset{\text { (fructose) }}{ C _6 H _{12} O _6}$
Inversion of sugar cane
(d) $2 SO _2( g )+ O _2( g ) \xrightarrow{ NO ( g )}2 SO _3( g )$

A

(A) and (B) only

B

(B) and (C) only

C

(A) and (C) only

D

(C) and (D) only

Solution

$Rb$ & $Cs$ have nearly same electron gain enthalpy electron gain enthalpy $=-46 kj / ml\, Ar$ & $Kr$ have same $\Delta H _{ eq }$. Value is $+96$ $kj / ml$

A

$2 Cu _2 S +3 O _2 \rightarrow 2 Cu _2 O +2 SO _2$

B

$Fe _3 O _4+ CO \rightarrow 3 FeO + CO _2$

C

$Al _2 O _3+2 NaOH +3 H _2 O \rightarrow 2 Na \left[ Al ( OH )_4\right]$

D

$Al _2 O _3+6 Mg \rightarrow 6 MgO +4 Al$

Solution

$Al _2 O _3+2 NaOH +3 H _2 O \rightarrow 2 Na ,\left[ Al ( OH )_4\right]$ Leaching.

A

$Ca ( OH )_2$ and $Mg ( OH )_2$

B

$CaCO _3$ and $Mg ( OH )_2$

C

$Ca ( OH )_2$ and $MgCO _3$

D

$CaCO _3$ and $MgCO _3$

Solution

Clark's Method Reaction
$Ca \left( HCO _3\right)_2+ Ca ( OH )_2 \rightarrow 2 CaCO _3+2 H _2 O $
$Mg \left( HCO _3\right)_2+2 Ca ( OH )_2 \rightarrow 2 CaCO _3+ Mg ( OH )_2+2 H _2 O$

A

Low solubility of LiF in water is due to its small hydration enthalpy.

B

$KO _2$ is paramagnetic.

C

Solution of sodium in liquid ammonia is conducting in nature.

D

Sodium metal has higher density than

Solution

Low solubility of LiF in water is due to high lattice enthalpy

A

(A) - (II), (B) - (III), (C) - (I), (D) - (IV)

B

(A) - (III), (B) - (I), (C) - (IV), (D) - (II)

C

(A) - (II), (B) - (IV), (C) - (I), (D) - (III)

D

(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

Solution

$\left( NH _4\right)_2 Cr _2 O _7 \xrightarrow{\Delta} N _2+ Cr _2 O _3+4 H _2 O$
$KMnO _4+ HCl \rightarrow MnCl _2+ KCl + Cl _2+ H _2 O$
$Al + NaOH + H _2 O \rightarrow H _2+ Na \left[ Al ( OH )_4\right]$
$NaNO _3 \longrightarrow NaNO _2+ O _2$

A

Cu

B

Mn

C

Ni

D

Zn

Solution

Copper is least electropositive among the given metals and it lies below H in reactivity series

A

Both Statement I and Statement II are true

B

Both Statement I and Statement II are false

C

Statement I is true but Statement II is false

D

Statement I is false but Statement II is true

Solution

Since eutrophication is result of excessive growth of weed in water bodies, which consume dissolved oxygen of water bodies.
$\therefore$ Eutrophication decreases amount of dissolved oxygen in water bodies.
Polluted water has low value of dissolved oxygen, but high valueof BOD (Biological oxygen demand), since chemical and organic matter requires dissolved oxygen to get decompose.

A

(A) - (II), (B) - (I), (C) - (IV), (D) - (III)

B

(A) - (IV), (B) - (III), (C) - (I), (D) - (II)

C

(A) - (III), (B) - (IV), (C) - (I), (D) - (II)

D

(A) - (IV), (B) - (III), (C) - (II), (D) - (I)

A

'A' and 'B' are both Markovnikov addition products.

B

' $A$ ' is Markovnikov product and ' $B$ ' is anti-Markovnikov product.

C

'A' and 'B' are both anti-Markovnikov products.

D

' $B$ ' is Markovnikov and ' $A$ ' is anti-Markovnikov product.

A

B

C

D

Solution

A

B

C

D

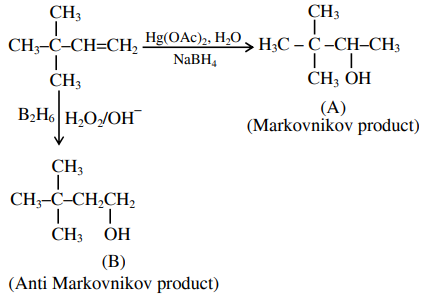
A

$A - CH _3 CH _2 CH = CH - CH _3$, $B - CH _3 CH _2 CH _2 CH = CH _2$, Saytzeff products

B

$A - CH _3 CH _2 CH = CH - CH _3$, B $- CH _3 CH _2 CH _2 CH = CH _2$, Hafmann products

C

$A - CH _3 CH _2 CH _2 CH = CH _2$, B $- CH _3 CH _2 CH = CHCH _3$, Hofmann products

D

$A - CH _3 CH _2 CH _2 CH = CH _2$, B $- CH _3 CH _2 CH = CHCH _3$, Saytzeff products

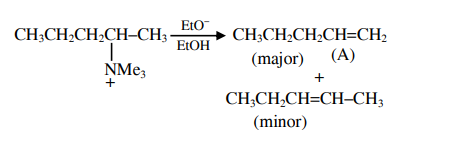
A

Ethane-1, 2-diol and Benzene-1, 3 dicarboxylic acid

B

Propane-1, 2-diol and Benzene-1, 4 dicarboxylic acid

C

Ethane-1, 2-diol and Benzene-1, 4 dicarboxylic acid

D

Ethane-1, 2-diol and Benzene-1, 2 dicarboxylic acid

A

B

C

D

A

$(A), (D) $only

B

$( A ),( C )$ only

C

$(A), (B) $only

D

$( A ),( B ),( C )$ only

Solution

Enzyme inhibitors can be competitive inhibitors (inhibit the attachment of substrate on active site of enzyme) and non competitive inhibitor (changes the active site of enzyme after binding at allosteric site.)

A

(A), (B), (C) only

B

(A), (D), (E) only

C

(D), (E) only

D

(A), (B), (E) only

Solution

The is recorded immediately after the blue colour appears.
$Na _2 S _2 O _3$ is kept in limited amount.

Solution

$\underset{1 \text{mol }}{ X }+\underset{ 1 \text{mol }}{ Y }+\underset{0.05 \text{mol} }{3 Z } \rightleftharpoons X Y Z _ { 3 }$
$Z$ is L.R.
$ \frac{0.05}{3}=1 \text { mole of } XYZ _3$
$ \text { Mass of } XYZ _3=\frac{0.05}{3} \times(10+20+30 \times 3)$
$ =2 g$

Solution

$M$ is body certred cubic,
$\therefore Z =2$
Let mass of 1 atom of $M$ is $A$
Edge length $=300\, pm$
Density $=6\, g / cm ^3$
$\therefore 6 \, g / cm ^3=\frac{ Z \times A }{\left(300 \times 10^{-10}\right)^3}=\frac{2 \times A }{27 \times 10^{-24}}$
$A =81 \times 10^{-24} g$
$\therefore$ Atomic mass $=48.6\, g$
$\therefore$ Mole in $180 g =\frac{180}{48.6}=3.7\, moles$
Atoms of $M =3.7 \times 6 \times 10^{23}$
$=22.22 \times 10^{23}$ atoms

Solution

Paramagnetic $B _2, C _2^{-}, O _2^{+}, He _2^{+}$

Solution

$ 150 \,g \,CH _3 COOH $
$ 10.2 g \text { ascorbic acid } \Rightarrow 0.058 \text { moles } $
$ \Delta T _{ f }=\left( x \times 10^{-1}\right){ }^{\circ} C $
$ \Delta T _{ f }= k _{ f } \cdot \text { molality } $
$ =3.9 \times \frac{0.058}{150} \times 1000$
$ =1.5^{\circ} C $
$ =15 \times 10^{-1}{ }^{\circ} C $

Solution

$K _{ a }$ of Butyric acid $\Rightarrow 2 \times 10^{-5} PKa =4.7$
$pH$ of $0.2 M$ solution
$ pH =\frac{1}{2} pK _{ a }-\frac{1}{2} \log C$
$ =\frac{1}{2}(4 \cdot 7) \frac{1}{2} \log (0.2)$
$=2.35+0.35=2.7$
$pH =27 \times 10^{-1}$

Solution

$ A \rightarrow B $
$t _{1 / 2}=0.3010 \min $
$ A _0 / A _{ t } \text { at time } 2 \min =\text { ? }$
$ K =\frac{2.303}{ t } \log \left[\frac{ A _0}{ A _{ t }}\right] $
$ \Rightarrow \frac{0 \cdot 693}{ t _{\frac{1}{2}}}=\frac{2 \cdot 303}{2} \log \left(\frac{ A _0}{ A _{ t }}\right) $
$ \text { Or } \frac{2.303 \times 0.3010}{0.3010}=\frac{2.303}{2} \log \frac{A_0}{A_t} $
$ \log \frac{A_0}{A_t}=2 $
$ \therefore \frac{ A _0}{ A _{ t }}=10^2=100$

Solution

Square pyramidal structures are $BrF _5, IF _5$ and $ClF _5$.

Solution

$MnO _4^{2-} \stackrel{ H ^{+}}{\longrightarrow} MnO _4^{-}+ MnO _2$
No. of unpaired $\overline{ e }=3$
$\therefore \mu=\sqrt{15}=3.877$
Nearest Integer $=4$

Solution

$0.492\, g$ of $C _{ x } H _{ y } O _z$
Gives $0.7938 \, g \, CO _2=0.018$ moles
$0.4428\, g\, H _2 O =0.0246$ moles
So moles of $C =0.018 \Rightarrow 0.216\, g$
Moles of $H =0.049 \Rightarrow 0.049\, g$
$\therefore$ wt. of Oxygen $=0.492-0.216-0.049$
$=0.227\, g$
$\%$ of Oxygen $=\frac{0.227}{0.492} \times 10046$ (approx.)

A

$\frac{1}{2}$

B

$\frac{3}{2}$

C

$-\frac{3}{2}$

D

$\frac{5}{2}$

Solution

$ x d y=\left(\sqrt{x^2+y^2}+y\right) d x $
$ x d y-y d x=\sqrt{x^2+y^2} d x $
$ \frac{x d y-y d x}{x^2}=\sqrt{1+\frac{y^2}{x^2}} \cdot \frac{d x}{x} $
$ \frac{d(y / x)}{\sqrt{1+\left(\frac{y}{x}\right)^2}}=\frac{d x}{x} $
$ \ln \left(\frac{y}{x}+\sqrt{\left(\frac{y}{x}\right)^2+1}\right)=\ln x+R $
$ \frac{y+\sqrt{y^2+x^2}}{x}=c x$
$ y +\sqrt{ y ^2+ x ^2}= cx ^2$
$ x =1, y =0 \Rightarrow 0+1= C \Rightarrow C =1 $
Curve is $y +\sqrt{ x ^2+ y ^2}= x ^2$
$x =2, y =\alpha$
$ 2+\sqrt{4+\alpha^2}=4 $
$ 4+\alpha^2=16+\alpha^2=8 \alpha $
$\alpha=\frac{3}{2}$

A

$\left(-\infty, \frac{1}{4}\right]$

B

$\left[-\frac{1}{4}, \infty\right)$

C

$\left(-\frac{1}{3}, \infty\right)$

D

$\left(-\infty, \frac{1}{3}\right]$

Solution

$ \left|\frac{x^2+4 x+2}{x^2+3}\right| \leq 1$
$ \Leftrightarrow \left(x^2-4 x+2\right)^2 \leq\left(x^2+3\right)^2$
$\Leftrightarrow \left(x^2-4 x+2\right)^2-\left(x^2+3\right)^2 \leq 0 $
$\Leftrightarrow \left(2 x^2-4 x+5\right)(-4 x-1) \leq 0 $
$ \Leftrightarrow -4 x-1 \leq 0 \rightarrow x \geq-\frac{1}{4}$

A

a non-empty finite set

B

equal to $N$

C

equal to $R -\{0\}$

D

equal to $R$

Solution

By its given condition
$: \vec{a}, \vec{b}, \vec{c}$ are linearly independent vectors
$\Rightarrow[\overline{ a } \overline{ b } \overline{ c }] \neq 0$...(i)
Now, $[\bar{a} \bar{b} \bar{c}]$
$\ =\begin{vmatrix}1+ t & 1- t & 1 \\ 1- t & 1+ t & 2 \\ t & - t & 1\end{vmatrix} $
$ C _2 \rightarrow C _1+ C _2 $
$ \begin{vmatrix}1+ t & 2 & 1 \\ 1- t & 2 & 2 \\ t & 0 & 1\end{vmatrix} $
$=2 \begin{vmatrix}1+ t & 1 & 1 \\ 1- t & 1 & 2 \\ t & 0 & 1\end{vmatrix} $
$ =2[(1+ t )-(1- t )+ t ] $
$ =2[3 t ]=6 t $
$ {[\overline{ a } \overline{ b } \overline{ c }] \neq 0 \Rightarrow t \neq 0}$

A

0

B

1

C

$\frac{1}{2}$

D

$-\frac{1}{2}$

Solution

$ \cos ^{-1} x=2 \sin ^{-1} x=\cos ^{-1} 2 x$
$ \cos ^{-1} x-2\left(\frac{\pi}{2}-\cos ^{-1} x\right)=\cos ^{-1} 2 x$
$ \cos ^{-1} x -\pi+2 \cos ^{-1} x =\cos ^{-1} 2 x$
$ 3 \cos ^2 x =\pi+\cos ^{-1} 2 x$...(i)
$ \cos \left(3 \cos ^{-1} x \right)=\cos \left(\pi+\cos ^{-1} 2 x\right) $
$4 x^3-3 x=-2 x$
$4 x^3=x \Rightarrow x=0, \pm \frac{1}{2}$
All satisfy the original equation
$\text { sum }=-\frac{1}{2} \text { to }+\frac{1}{2}=0$

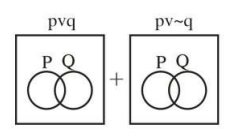
A

$(\vee, \wedge)$

B

$(\vee, \vee)$

C

$(\wedge, \wedge)$

D

$(\wedge, \vee)$

Solution

Well check each option
For A $\pi=\operatorname{vof} 0=\Lambda$
$ ( pvq ) \wedge( pv \sim q )$
$ \equiv pv ( q \wedge \sim q ) $
$\equiv pv ( c ) \equiv p$
For $B : * =v, O=v$
$( pvq ) \vee( pv \sim q ) \equiv t$ using Venn Diagrams

A

$9 \sqrt{3}$

B

$27 \sqrt{3}$

C

9

D

81

Solution

$|\vec{a}|=9 \&(x \vec{a}+y \vec{b}) \cdot(6 y \vec{a}-18 x \vec{b})=0$
$\Rightarrow 6 x y|\bar{a}|^2-18 x^2(\overline{ a } \cdot \overline{ b })+6 y ^2(\overline{ a } \cdot \overline{ b })-18 xy |\overline{ b }|^2=0$
$\Rightarrow 6 x y\left(|\overrightarrow{ a }|^2-3|\overline{ b }|^2\right)+(\overline{ a } \cdot \overline{ b })\left( y ^2-3 x ^2\right)=0 $
$ \text { This should hold } \forall x , y \in R \times R$
$\therefore|\overline{ a }|^2=3|\overline{ b }|^2 \&(\overline{ a } \cdot \overline{ b })=0 $
$ \text { Now }|\overline{ a } \times \overline{ b }|^2=|\overline{ a }|^2|\overline{ b }|^2-(\overline{ a } \cdot \overline{ b })^2 $
$=|\overline{ a }|^2 \cdot \frac{|\overline{ a }|^2}{3} $
$ \therefore |\overline{ a } \times \overline{ b }|=\frac{|\overline{ a }|^2}{\sqrt{3}}=\frac{81}{\sqrt{3}}=27 \sqrt{3}$

A

$\frac{8}{3}$

B

8

C

$\frac{77}{9}$

D

$\frac{80}{9}$

Solution

$s \equiv \sin t , c \equiv \cos t$
Let orthocentre be $( h , k )$
Since it if an equilateral triangle hence orthocentre coincides with centroid.
$\therefore a + s + c =3 h , b + s - c =3 k$
$ \therefore (3 h - a )^2+(3 k - b )^2=( s + c )^2+( s - c )^2=2\left( s ^2+ c ^2\right)=2$
$ \therefore\left( h -\frac{ a }{3}\right)^2+\left( K -\frac{ b }{3}\right)^2=\frac{2}{9} $
$ \text { circle centre at }\left(\frac{ a }{3}, \frac{ b }{3}\right)$
$ \text { Gives, } \frac{ a }{3}=1, \frac{ b }{3}=\frac{1}{3} \Rightarrow a =3, b =1 $
$ \therefore a ^2- b ^2=8$

A

$\alpha=14$

B

$\alpha$ is a multiple of 4

C

4 is the remainder when $\alpha$ is divided by 10

D

4 is the remainder when $\alpha$ is divided by 7

Solution

For $R$ to be reflexive $\Rightarrow x R x$
$ \Rightarrow 3 x +\alpha x =7 x \Rightarrow(3+\alpha) x =7 K $
$ \Rightarrow 3+\alpha=7 \lambda \Rightarrow \alpha=7 \lambda-3=7 N +4, K , \lambda, N \in I$
$\therefore$ when $\alpha$ divided by 7 , remainder is 4 .
$R$ to be symmetric $x R y \Rightarrow y R x$
$3 x +\alpha y =7 N _1, 3 y +\alpha x =7 N _2 $
$\Rightarrow(3+\alpha)( x + y )=7\left( N _1+ N _2\right)=7 N _3$
Which holds when $3+\alpha$ is multiple of 7
$\therefore \alpha=7 N +4 \text { (as did earlier) }$
$R$ to be transitive
$x R y \& y R z \Rightarrow x R z$.
$3 x +\alpha y =7 N _1 \& 3 y +\alpha z =7 N _2 $ and $3 x +\alpha z =7 N _3$
$\therefore 3 x +7 N _2-3 y =7 N _3$
$\therefore 7 N _1-\alpha y +7 N _2-3 y =7 N _3$
$\therefore 7\left( N _1+ N _2\right)-(3+\alpha) y =7 N _3$
$\therefore(3+\alpha) y =7 N$
Which is true again when $3+\alpha$ divisible by
7, i.e. when $\alpha$ divided by 7 , remainder is 4 .

A

$\frac{3}{4}$

B

$\frac{11}{16}$

C

$\frac{23}{32}$

D

$\frac{13}{16}$

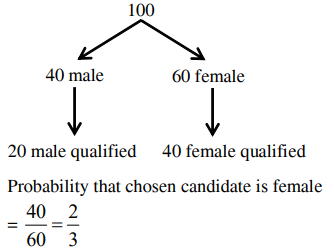
A

$\frac{2}{\sqrt{3}} e ^{-2 \pi / 3}$

B

$\frac{2}{\sqrt{3}} e ^{2 \pi / 3}$

C

$\frac{1}{\sqrt{3}} e ^{-2 \pi / 3}$

D

$\frac{1}{\sqrt{3}} e ^{2 \pi / 3}$

Solution

Given differential equation can be re-written as
$\frac{d y}{d x}+(8+4 \cot 2 x) y=\frac{2 e^{-4 x}}{\sin ^2 2 x}(2 \sin x+\cos 2 x)$
which is a linear diff. equation.
$\text { I.f. } =e^{\int(8+4 \cot 2 x) d x}=e^{8 x+2 C u(\sin 2 x)} $
$ =e^{8 x} \cdot \sin ^2 2 x$
$\therefore$ solution is
$y\left(e^{8 x} \cdot \sin ^2 2 x\right) =\int 2 e^{4 x}(2 \sin 2 x+\cos 2 x) d x+C $
$ =e^{4 x} \cdot \sin 2 x+C$
Given $y \left(\frac{\pi}{4}\right)= e ^{-\pi} \Rightarrow C =0$
$ \therefore y =\frac{ e ^{-4 x}}{\sin 2 x } $
$ \therefore y \left(\frac{\pi}{6}\right)=\frac{ e ^{-4 \cdot \frac{\pi}{6}}}{\sin \left(2 \cdot \frac{\pi}{6}\right)}=\frac{2}{\sqrt{3}} e ^{-\frac{2 \pi}{3}}$

A

$(0,1)$

B

$(2,-1)$

C

$(6,3)$

D

$(2,1)$

Solution

$y^2=2 x-3$ ...(1)
Equation of chord of contact
$PQ : r =0$
$yx 1=( x +0)-3$
$y=x-3$...(2)

from (1) and (2)
$(x \cdot 3)^2=2 x-3 $
$ x^2-8 x+12=0$
$ (x-2)(x-6)=0 $
$ x=2 \text { or } 6$
$ y=-1 \text { or } 3$

$MQR =\frac{2}{6}=\frac{1}{3} $
$ MPR =\frac{2}{6}=\frac{1}{3} $
$ MPR =\frac{2}{-2}=-1 $
$ MPQ \times MPR =-\Rightarrow PQ \perp PR$
$ \text { Orthocentre }= P (2,-1)$

A

2

B

$2 \sqrt{2}$

C

$8 \sin \left(\frac{\pi}{8}\right)$

D

$8 \cos \left(\frac{\pi}{8}\right)$

Solution

$ x^2+y^2-x+2 y=\frac{11}{4} $
$ \left(x-\frac{1}{2}\right)^2+(y+1)^2=(2)^2$
Or $\triangle PQR$
$PR = QK \sin 2 \geq \frac{1}{3}$

$ PQ = QR \cos 22 \frac{1}{2} $
$ =4 \cos \frac{\pi}{8} $
$ \text { As } \triangle PQR =\frac{1}{2} PR \times PQ$
$ =\frac{1}{2}\left(4^2 \sin \frac{\pi}{6}\right)\left(4 \cos \frac{\pi}{8}\right) $
$=4 \sin \frac{\pi}{4}=\frac{4}{\sqrt{2}}=2 \sqrt{2} $

A

0

B

2

C

3

D

4

Solution

$ 7^{2022}+3^{2022} $
$=(49)^{1011}+(9)^{1011} $
$ =(50-1)^{1011}+(10-1)^{1011}$
$ =5 \lambda-1+5 K -1 $
$ =5 m -2 $
Remainder $=5-2=3$

A

$3^{28}$

B

$3^{30}$

C

$3^{32}$

D

$3^{36}$

Solution

$A^2=\begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0\end{bmatrix}$
$=\begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix}$
$ a \leftrightarrow R _2$
$-\begin{bmatrix}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{bmatrix}$
$R _2 \leftrightarrow R _3$
$\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}=I$
$B _0= A ^{49}+2 A ^{98} $
$ = A +2 I $
$ B _{ n } =\text{Adj}\left( B _{ n }-1\right) $
$B_4=\text{Adj}\left(\text{Adj}\left(\text{Adj}\left(\text{Adj}_0\right)\right)\right.$
$ =\left| B _0\right|^{( n -1)^4}$
$=\left| B _0\right|^{16}$
$B_0=\begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0\end{bmatrix}+\begin{bmatrix}2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{bmatrix}$
$=\begin{bmatrix}2 & 1 & 0 \\ 0 & 2 & 1 \\ 1 & 0 & 2\end{bmatrix}$
$ =2(4-0)-1(0-1) $
$ =9 $
$ B _4(9)^{16}=(3)^{32}$

A

0

B

$\frac{1}{2}$

C

$\frac{3}{2}$

D

$\frac{5}{2}$

Solution

$ \left| z _2+\right| z _2-\left.1\right|^2=\left| z _2-\right| z _2+\left.1\right|^2 $
$ \Rightarrow \left| z _2+\right| z _2-1||\left(\overline{ z }_2+\left| z _2-1\right|\right)=\left( z _2-\left| z _2+1\right|\right)\left(\overline{ z }_2-\left( z _2+1\right)\right)$
$\Rightarrow z _2\left|\overline{ z }_2+12_2-1\right|-\left(\overline{ z }_2-\left| z _2+1\right|\right)+\overline{ z }_2\left(\left| z _2-1\right|+\left| z _2+1\right|\right)$
$=\left| z _2+1\right|^2=\left| z _2-1\right|^2$
$ \Rightarrow\left[ z _2+\overline{ z }_2\right)\left(\left| z _2-1\right|\right)+\left( z _2+1 \mid\right)=2\left( z _2+\overline{ z }_2\right) $
$\Rightarrow\left( z _2+\overline{ z }_2\right)\left(\left| z _2-1\right|+\left| z _2+1\right|-2\right)=0 $
$ \therefore z _2+\overline{ z }_2=0 \text { or }\left| z _2-1\right|+\left| z _2+1\right|-2=0$
$\therefore z _2$ lie on imaginary axis. Or on real axis with in $[-1,1]$
Also $\left|z_1-3\right|=\frac{1}{2}$ lie on circle having centre 3 and radius $\frac{1}{2}$.

Clearly $\left|z_1-z_2\right| \min =\frac{5}{2}-1=\frac{3}{2}$

A

$(6 x+5 y-12)^2+4(3 x+7 y-8)^2=1$, $z=6-2 x-3 y$

B

$(5 x+6 y-12)^2+4(3 x+5 y-9)^2=1$, $z=6-2 x-3 y$

C

$(6 x+5 y-14)^2+9(3 x+5 y-7)^2=1$, $z=6-2 x-3 y$

D

$(5 x+6 y-14)^2+9(3 x+7 y-8)^2=1$, $z=6-2 x-3 y$

Solution

$ \frac{ h -\cos \theta}{2}=\frac{ k -\sin \theta}{3}=\frac{ w -0}{1} $
$ =\frac{-1(2 \cos \theta+3 \sin \theta-6)}{14} $
$ h =\cos \frac{-2(2 \cos \theta+3 \sin \theta-6)}{14} $
$ =\frac{10 \cos \theta-6 \sin \theta+12}{14} $
$ k =\sin \theta-\frac{3}{14}(2 \cos \theta+3 \sin \theta-6) $
$ k =\frac{5 \sin \theta-6 \cos \theta+18}{14}$
Elementary $\sin \theta$ and $\cos \theta$
$(5 h+6 k-12)^2+4(3 h+5 k-9)^2=1$

A

32

B

64

C

128

D

256

Solution

$\frac{x^2}{2}+\frac{x^2}{2}+\frac{x^2}{2}+\frac{x^2}{2}+\frac{x^2}{2}+\frac{\alpha}{2 x^5}+\frac{\alpha}{2 x^5} $
$ \geq 7\left(\frac{\alpha^2}{2^7}\right)^{\frac{1}{7}} $
$\frac{7 \cdot(\alpha)^{2 / 7}}{2}=14 $
$ \left(\alpha^2\right)^{1 / 7}=2^2$
$ \alpha=\left(2^2\right)^{7 / 2}=2^7$
$ \alpha=128$

A

0

B

3

C

9

D

27

Solution

Consider a case when $\alpha=\beta=0$ then
$f(x)=y x$
$g(x)=\frac{x}{y}$
$ \frac{1}{ n } \displaystyle\sum_{ i =1}^{ n } f \left( a _{ i }\right) \Rightarrow \frac{ y }{ n }\left( a _1+ a _2+\ldots . .+ a _{ n }\right) $
$ =0 $
$ \Rightarrow f ( g (0)) \Rightarrow f (0) $
$ \Rightarrow 0$

A

$-30$

B

$-31$

C

$-60$

D

$-61$

Solution

$a_{n+2} a_{n+1}-a_{n+1} \cdot a_n=2$
Series will satisfy

$ \frac{a_n+\frac{1}{a_{n+1}}}{a_{n+2}}=\frac{a_{n+2}-\frac{1}{a_{n+1}}}{a_{n+2}} $
$=1-\frac{1}{a_{n+1} a_{n+2}} $
$ =1-\frac{1}{2(r+1)} $
$ =\frac{2 r+1}{2(r+1)}$
Now proof is given by
$ =\displaystyle\prod_{ r =1}^{30} \frac{(2 r +1)}{2( r +1)}$
$ =\frac{(1 \cdot 3 \cdot 5 \cdot \ldots \ldots . .61)}{2^{30} \cdot(2 \cdot 3 \cdot \ldots \ldots .31)} $

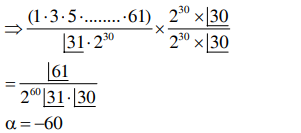
A

$-\frac{2}{\sqrt{ e }}$

B

$-2 \sqrt{e}$

C

$-\sqrt{ e }$

D

$\frac{2}{\sqrt{e}}$

Solution

$ f(x)=e^x \cdot \int\limits_0^x \frac{f^{\prime}(t)}{e^t} d t $
$ f^{\prime}(x)=e^x \cdot \int\limits_0^x \frac{f^{\prime}(t)}{e^t} d t+e^x \cdot \frac{f^{\prime}(x)}{e^x}$
$-\left[(2 x-1) \cdot e^x+\left(x^2-x+1\right) \cdot e^x\right]$
$\int\limits_0^x \frac{f^{\prime}(t)}{e^t} d t=x^2+x $
$ \frac{f^{\prime}(x)}{e^x}=2 x+1 $
$ f^{\prime}(x)=(2 x+1) \cdot e^x $$
f^{\prime}(x)=0 \Rightarrow x=-\frac{1}{2}$
$ f(x)=(2 x+1) \cdot e^x-2 e^x+C$

$-1=1-2+C $
$ C=0 $
$ f(x)=e^x(2 x-1) $
$ f\left(-\frac{1}{2}\right)=\frac{-2}{\sqrt{e}}$

Solution

Required no. $=$ Total $-$ no character from $\{1,2,3$, $4,5\}$
$ =\left(10^6-5^6\right)+\left(10^7-5^7\right)+\left(10^8-5^8\right)$
$ =10^6(1+10+100)-5^6(1+5+25) $
$ =10^6 \times 111-5^6 \times 31 $
$ =2^6 \times 5^6 \times 111-5^6 \times 31$
$ =5^6\left(2^6 \times 111-31\right) $
$ =5^6 \times \underbrace{7073}_a $
$ \therefore \alpha=7073$

Solution

$RS \equiv(\alpha,-1, \beta)$
$DR$ of $PQ \equiv\left(\frac{56}{17}+2, \frac{43}{17}+1, \frac{111}{17}-1\right)$
$ \equiv\left(\frac{90}{17}, \frac{60}{17}, \frac{94}{17}\right) $
$\frac{90}{17} \alpha+\frac{60}{17}(-1)+\frac{94}{17} \beta=0 $
$ 90 \alpha+94 \beta=60 $
$ \beta=\frac{60-90 \alpha}{94}$
$ \beta=\frac{30(2-3 \alpha)}{94} $
$ \beta=-30 \frac{(3 \alpha-2)}{94} $
$ \beta=\frac{-15}{47}(3 \alpha-2) $
$\Rightarrow \frac{\beta}{-15}=\frac{3 \alpha-2}{47} $
$ \Rightarrow \beta=-15, \alpha=-15 $
$ \alpha^2+\beta^2=225+225 $
$ =450$

Solution

$ f^{\prime}(a)=f^{\prime}(b)=f^{\prime}(c)=2$
$ \Rightarrow f^{\prime \prime}(x) \text { is zero }$
for atleast $x_1 \in(a, b) \& x_2 \in(b, c)$

Solution

Put $1+x^2=t^2$
$2 dx =2 t dt$
$X dx = t dt$
$\therefore \int \limits_1^2 \frac{15\left( t ^2-1\right) tdt }{\sqrt{ t ^2+ t ^3}}$
$15 \int \limits_1^2 \frac{ t \left( t ^2-1\right)}{ t \sqrt{1+ t }} dt$
Put $1+ t = u ^2$
$dt =2 u du$
$15 \int \limits_{\sqrt{2}}^{\sqrt{3}} \frac{\left(u^2-1\right)^2-1}{u} \times 2 u d u$
$30 \int \limits_{\sqrt{2}}^{\sqrt{3}}\left(u^4-2 u^2\right) d u$
$ 30\left(\frac{ u ^5}{5}-\frac{2 u ^3}{3}\right)_{\sqrt{2}}^{\sqrt{3}} $
$ 30\left[\frac{1}{5}\left(\sqrt{3}^5-\sqrt{2}^5\right)-\frac{2}{3}\left(\sqrt{3}^3-\sqrt{2}^3\right)\right] $
$ 30\left[\frac{1}{5}(9 \sqrt{3}-4 \sqrt{2})-\frac{2}{3}(3 \sqrt{3}-2 \sqrt{2})\right] $
$30\left[-\frac{1}{5} \times \sqrt{3}+\frac{8}{15} \sqrt{2}\right]$
$ -6 \sqrt{3}+16 \sqrt{2}=\alpha \sqrt{2}+\beta \sqrt{3} $
$\alpha=16, \beta=-6 $
$\therefore \alpha+\beta=10$

Solution

Solution

$f(x)=0 \Rightarrow(x-p)^2-q=0$
Roots are $p +\sqrt{ q }, p -\sqrt{ q }$ absolute difference between roots $2 \sqrt{q}$.
Now, $\left|f\left(a_i\right)\right|=500$
Let $a_1, a_2, a_3, a_4$ are $a_1 a+d, a+2 d, a+3 d$
$ \left|f\left(a_4\right)\right|=500 $
$ \left|\left(a_1-p\right)^2-q\right|=500$
$ \Rightarrow\left(a_1-p\right)^2-q=500$
$ \Rightarrow \frac{9}{4} d^2-q=500$ ....(1)

$ \text { and }\left|f\left(a_1\right)\right|^2=\left|f\left(a_2\right)\right|^2$
$ \left(\left(a_1-p\right)^2-q\right)^2=\left(\left(a_2-p\right)^2-q\right)^2$
$ \Rightarrow\left(\left(a_1-p\right)^2-\left(a_2-p\right)^2\right)\left(\left(a_1-p\right)^2-q+\left(a_2-p\right)^2-q\right)=0 $
$ \Rightarrow \frac{9}{4} d^2-q+\frac{d^2}{4}-q=0 $
$ 2 q =\frac{10 d^2}{4} \Rightarrow q=\frac{5 d^2}{4} $
$\Rightarrow d^2=\frac{4 q}{5}$
From equation (1) $\frac{9}{4} \cdot \frac{4 \cdot q}{5}-q=500$
$ \frac{4 q}{5}=500 $
$\frac{4 q}{5}=500$
and $2 \sqrt{ q }=2 \times \frac{50}{2}=50$

Solution

$e _{ E }=\sqrt{1-\frac{ b ^2}{ a ^2}}, e _{ H }=\sqrt{2} $
$\text { If } \Rightarrow e _{ E }=\frac{1}{ e _{ H }} $
$ \Rightarrow \frac{ a ^2- b ^2}{ a ^2}=\frac{1}{2}$
$ 2 a ^{2-2 b} 2= a ^2 $
$ a ^2=2 b ^2$
and $y =\sqrt{\frac{5}{2}} x + k$ is tangent to ellipse then
$K ^2= a ^2 \times \frac{5}{2}+ b ^2=\frac{3}{2}$
$6 b^2=\frac{3}{2} \Rightarrow b^2=\frac{1}{4}$ and $a^2=\frac{1}{2}$
$\therefore 4 \cdot\left(a^2+b^2\right)=3$

Solution

$\sum_{ x _0^1}^1=\frac{3\left(1-\left(\frac{1}{2}\right)\right)^{20}}{1 \frac{-1}{2}}=6\left(1-\frac{1}{2^{20}}\right) $
$ =\displaystyle\sum_{ i =1}^{20}\left( x _{ i - i }\right)^2 $
$=\displaystyle\sum_{ i =1}^{20}\left( x _{ i }\right)^2+( i )^2-2 x _{ i } i $
$ \text { Now }=\sum_{ i =1}^{20}\left( x _{ i }\right)^2=\frac{9\left(1-\left(\frac{1}{4}\right)\right)^{20}}{1-\frac{1}{4}}=12\left(1-\frac{1}{2^{40}}\right) $
$ \displaystyle\sum_{ i =1}^{20} i ^2=\frac{1}{6} \times 20 \times 21 \times 41=2870$
$\displaystyle\sum_{ i =1}^{20} x _{ i } i = s =3+2.3 \frac{1}{2}+3.3 \frac{1}{2^2}+4.3 \frac{1}{2^3}+\ldots \ldots . AGP $
$ =6\left(2-\frac{22}{2^{20}}\right) $
$ \overline{ x } =\frac{12-\frac{12}{2^{40}}+2870-12\left(2-\frac{22}{2^{20}}\right)}{20} $
$ \overline{ x } =\frac{2858}{20}+\left(\frac{-12}{2^{40}}+\frac{22}{2^{20}}\right) \times \frac{1}{20} \\ {[\overline{ x }] } =142$

Solution

$\lim _{x \rightarrow 10}\left(\frac{(x+2 \cos x)^3+2(x+2 \cos x)^2+3 \sin (x+2 \cos x)}{(x+2)^3+2(x+2)^2+3 \sin (x+2)}\right)^x$
Form $1^{\infty}$
$ = e ^{\lim _{x \rightarrow 0}\left[\left(\frac{(x+2 \cos x)^3+2(x+2 \cos x)^2+3 \sin (x+2 \cos x)}{(x+2)^3+2(x+2)^2+3 \sin (x+2)}\right)-1\right] \times \frac{100}{x}} $
$ =e^{\lim _{x \rightarrow 0}\left[\frac{100}{x}\left(\frac{(x+2 \cos x)^3+2(x+2 \cos x)^2+3 \sin (x+2 \cos x)-\left((x+2)^3+2(x+2)^2+3 \sin (x+2)\right)}{(x+2)^3+2(x+2)^2+3 \sin (x+2)}\right)\right]}$
$ =e^{\lim _{x \rightarrow 0} \frac{100}{x}\left[\left(\frac{(x+2 \cos x)^3+(x+2)^3+2(x+2 \cos x)^2-2(x+2)^2+3 \sin (x+2 \cos x)-3 \sin (x+2)}{8+8+3 \sin )^2}\right)\right]}$
$ = e ^{\frac{100}{16+3 \sin ^2} \lim _{x \rightarrow 0} \frac{3(x+2 \cos x)^2 \times(1+2 \sin x)-3(x+2)^2-4(x+2 \cos x)}{x(1-2 \sin x)-4(x+2)+3 \cos (x+2 \cos x) \times(1-2 \sin x)-3 \cos (x+2)}}$
$ = e ^{\frac{100}{16+3 \sin 2} 2}\left(\frac{12-3(4)+8 \times 1-8+3 \cos 2-3 \cos 2}{1}\right)$
Using L'H rule.
$= e ^{ o }=1$