JEE Main Physics Question Paper with Solution 2023 July 25th Shift 2 - Evening
A
$100 \%$
B
$80 \%$
C
$60 \%$
D
$50 \%$
Solution
modulation index $=\frac{ V _{\max }- V _{\min .}}{ V _{\max }+ V _{\min .}} \times 100 \%$
$ =\frac{6-2}{6+2} \times 100 \%=50 \%$
A
$\frac{5}{2}$
B
$\frac{25}{4}$
C
$\frac{5}{4}$
D
$\frac{25}{2}$
Solution
$ B =\frac{ N \mu_0 i }{2 R }$
$ B _1=\frac{ N _1 \mu_0 i }{2 R _1}$
For $ N _2=5$
Radius of coil $= R _2=\frac{ N _1 \times R _1}{ N _2}$
$ B _2=\frac{ N _2 \mu_0 i }{ R _2} $
$ \frac{ B _2}{ B _1}=\frac{ N _2}{ N _1} \cdot \frac{ R _1}{ R _2}=\frac{ N _2}{ N _1} \times \frac{ N _2}{ N _1} ; \frac{ B _2}{ B _1}=\frac{25}{4}$
A
$\frac{15}{\sqrt{2 \rho-\sigma}}$
B
$\frac{15}{\sqrt{\rho-\sigma}}$
C
$\frac{3}{2 \sqrt{\rho-\sigma}}$
D
$\frac{3}{20 \sqrt{2 \rho-\sigma}}$
Solution

Buoyant force $+$ surface tension $= mg$
$ \sigma \frac{ V }{2} g +2 \pi R T=\rho V g $
$2 \pi R T=\frac{(2 \rho-\sigma)}{2} \cdot \frac{4}{3} \pi R ^3 g ; \left[ V =\frac{4}{3} \pi R ^3\right]$
$R^3=\frac{3 T}{(2 \rho-\sigma) g} \Rightarrow R=\sqrt{\frac{3 \times 7.5 \times 10^{-2} N - m ^{-1}}{(2 \rho-\sigma) \times 10}}$
$R =\frac{3}{20 \sqrt{(2 \rho-\sigma)}} m =\frac{15}{\sqrt{2 \rho-\sigma}} cm$
A
100 N
B
200 N
C
300 N
D
400 N
Solution

Change in momentum of any one ball
$ |\Delta \overrightarrow{ P }|=2 \times 0.05 \times 10 $
$ |\Delta \overrightarrow{ P }|=1$
$ \left|\overrightarrow{ F }_{ av }\right|=\frac{|\Delta \overrightarrow{ P }|}{\Delta t } $
$ F _{ av }=200 \,N$
A
$\sqrt{2} N , 45^{\circ}$
B
$\sqrt{2} N , 135^{\circ}$
C
$\frac{2}{\sqrt{3}} N , 30^{\circ}$
D
$2 N , 45^{\circ}$
Solution
Let addition force required is $=\overrightarrow{ F }$
$ \overrightarrow{ F }+5 \hat{ i }-6 \hat{ i }+7 \hat{ j }-8 \hat{ j }=0$
$ \overrightarrow{ F }=\hat{ i }+\hat{ j },|\overrightarrow{ F }|=\sqrt{2}$
Angle with $x$-axis: $\tan \theta=\frac{ y \text { component }}{ x \text { component }}=\frac{1}{1}$
$\theta=45^{\circ}$
A
$\frac{n}{n-1}$
B
$\frac{2 n}{2 n+1}$
C
$\frac{ n +1}{ n }$
D
$\frac{2 n+1}{n}$
Solution
Capacitance of isolated Conducting sphere
$=4 \pi \varepsilon_0 R_1$
By enclosing inside another sphere of radius
$R_2 \text {, new capacitance }=\frac{4 \pi \varepsilon_0 R_1 R_2}{\left(R_2-R_1\right)}$
Given : $\frac{4 \pi \varepsilon_0 R_1 R_2}{\left(R_2-R_1\right)}=n \times 4 \pi \varepsilon_0 R_1$
$ \Rightarrow \frac{ R _2}{\left( R _2- R _1\right)}= n \Rightarrow \frac{\frac{ R _2}{ R _1}}{\left(\frac{ R _2}{ R _1}-1\right)}= n$
$\Rightarrow \frac{ R _2}{ R _1}= n \frac{ R _2}{ R _1}- n \Rightarrow \frac{ R _2}{ R _1}=\frac{ n }{( n -1)}$
A
$1: 1$
B
$\sqrt{2}: 1$
C
$2: 1$
D
$4: 1$
Solution
Kinetic energy gained by a charged particle accelerated by a potential $V$ is $qV$
$KE = qV $
$ \Rightarrow \frac{ p ^2}{2 m }= qV \Rightarrow p =\sqrt{2 mqV }$
$ p =\frac{ h }{\lambda}, \text { thus } \lambda=\frac{ h }{\sqrt{2 mqV }} $
now $ \frac{\lambda_{ p }}{\lambda_{ d }}=\sqrt{\frac{ m _{ d } V _{ d }}{ m _{ p } V _{ p }}}$
$ \Rightarrow \frac{1}{\sqrt{2}}=\sqrt{\frac{2 V _{ d }}{ V _{ p }}} \Rightarrow \frac{ V _{ p }}{ V _{ d }}=4$
A
0.8 m
B
3.2 m
C
1.2 m
D
5.6 m
Solution

Applying lens formula
$\frac{1}{0.12}+\frac{1}{2.4}=\frac{1}{ f } \Rightarrow \frac{1}{ f }=\frac{210}{24}$
Upon putting the glass slab, shift of image is
$\Delta x = t \left(1-\frac{1}{\mu}\right)=\frac{1}{3} cm$
Now $v =12-\frac{1}{3}=\frac{35}{3} cm$
Again apply lens formula
$\frac{1}{0.12}+\frac{1}{u}=\frac{1}{f}=\frac{210}{24}$
Solving $u =-5.6 m$
Thus shift of object is
$5.6-2.4=3.2 m$
A
$18 \times 10^{-7} T$
B
$54 \times 10^{-7} T$
C
$54 \times 10^{-8} T$
D
$18 \times 10^{-8} T$
Solution
$ E _{ y }=540 \sin \pi \times 10^4( x - ct ) Vm ^{-1} $
$ E _0=540 Vm ^{-1} $
$ B _0=\frac{ E _0}{ C }=\frac{540}{3 \times 10^8}=18 \times 10^{-7} T $
A
Electromagnetic induction
B
Resonance in ac circuits
C
Mutual induction in ac circuits
D
interference of electromagnetic waves
Solution
Metal detector works on the principle of transmitting an electromagnetic signal and analyses a return signal from the target. So it works on the principle of resonance in $AC$ circuit.
A
$1.6 \times 10^5 Hz$
B
$5.6 \times 10^5 Hz$
C
$2.8 \times 10^6 Hz$
D
$1.8 \times 10^6 Hz$
Solution
$f =\frac{1}{ T }=\frac{ eB }{2 \pi m } $
$ =\frac{1.6 \times 10^{-19} \times 10^{-4}}{2 \pi \times 9 \times 10^{-31}}=2.8 \times 10^6 Hz$
A
50 V
B
75 V
C
150 V
D
275 V
Solution

$ i _1=\frac{5}{10+5} \times 15 \,mA =5\, mA $
$ V _{ A }-5 i -10 i _1-10 i = V _{ B } $
$ V _{ A }- V _{ B }=75+50+150=275 \,V$
A
$\frac{2}{9} m$
B
$\frac{4}{9} m$
C
$\frac{8}{9} m$
D
$\frac{1}{9} m$
Solution
$ T =2 \pi \sqrt{\frac{ L }{ g }}, g ^{\prime}=\frac{ GM }{9 R ^2}=\frac{ g }{9}=\frac{\pi^2}{9} $
$ 2=2 \pi \sqrt{\frac{ L }{\pi^2} \times 9} $
$ \Rightarrow 1=\pi \sqrt{ L } \times \frac{3}{\pi} \Rightarrow L =\frac{1}{9} m $
A
1
B
2
C
3
D
4
Solution
$ v _{ S }=\sqrt{\frac{\gamma RT }{ M }} $
$ v _{ rms }=\sqrt{\frac{3 RT }{ M }} $
$ \frac{ v _{ s }}{ v _{ rms }}=\sqrt{\frac{\gamma}{3}}=\frac{1}{\sqrt{2}} \Rightarrow \frac{\gamma}{3}=\frac{1}{2} \Rightarrow \gamma=\frac{3}{2}$
$ \gamma=1+\frac{2}{ f _{\text {mix. }}}$
$ f _{\text {mix. }}=\frac{2 \times 3+ n \times 5}{ n +2}=\frac{6+ n \times 5}{( n +2)} $
$ \gamma=1+\frac{2( n +2)}{6+ n \times 5}=\frac{6+5 n +2 n +4}{6+5 n } $
$ \gamma=\frac{7 n +10}{6+5 n }=\frac{3}{2} $
$ 14 n +20=18+15 n$
$ n =2$
A
$0.41$
B
$0.56$
C
$0.73$
D
$0.70$
Solution
Efficiency $ \eta=1-\frac{ T _{ L }}{ T _{ H }}$
$ \eta_1=1-\frac{147+273}{447+273}=1-\frac{420}{720}$
$ \eta_1=\frac{300}{720} $
$ \eta_2=1-\frac{47+273}{947+273}=1-\frac{320}{1220} $
$\eta_2=\frac{900}{1220} $
$ \frac{\eta_1}{\eta_2}=\frac{300}{720} \times \frac{1220}{900}=\frac{122}{72 \times 3} $
$ \frac{\eta_1}{\eta_2}=0.56$
A
$36 \%$
B
$50 \%$
C
$64 \%$
D
$25 \%$
Solution

$g _{\text {eff }}=\frac{ g }{\left(1+\frac{ h }{ R }\right)^2} ; g _{\text {eff }}=\frac{ g }{\left(1+\frac{1}{4}\right)^2}=\frac{16 g }{25} $
change $=\frac{ g _{\text {eff }}- g }{ g } \times 100=\frac{\frac{16}{25}-1}{1} \times 100$
$ =\frac{-9}{25} \times 100=-36 \%$
A
$4.9 J$
B
$9.8 J$
C
$14.7 J$
D
$19.6 J$
Solution
$ P_{ i }=P_{ f }$ ( no any external force )
$ 0.2 \times 10=10 \times v$
$ v =0.2 \,m / sec $
Loss in K.E. $=\frac{1}{2} \times(0.2) \times 10^2-\frac{1}{2} \times 10(0.2)^2 $
$ =\frac{1}{2} \times 10 \times(0.2)[10-0.2] $
$ =9.8\, J $
A
$\frac{1}{4}$
B
$\frac{1}{2}$
C
2
D
4
Solution
$R = H$
$ \frac{2 v _{ x } \times v _{ y }}{ g }=\frac{ v _{ y }^2}{2 g }$
$ v _{ x }=\frac{ v _{ y }}{4} ; u \cos \theta=\frac{ u \sin \theta}{4} $
$ \tan \theta=4$
A
2
B
4
C
6
D
8
Solution
$ E _{ H }= I ^2 R \times t $
$\frac{\Delta E }{ E } \times 100=\frac{2 \Delta I }{ I } \times 100+\frac{\Delta R }{ R } \times 100+\frac{\Delta T }{ T } \times 100$
$ =2 \times 2+1+3=8$
A
$\sqrt{\frac{\lambda R }{\lambda-1}}$
B
$\sqrt{\frac{\lambda R}{\lambda R-1}}$
C
$\sqrt{\frac{\lambda}{\lambda R -1}}$
D
$\sqrt{\frac{\lambda R ^2}{\lambda R -1}}$
Solution

$ \frac{- Rch }{( n )^2}+\frac{ Rch }{1}=\frac{ hc }{\lambda} $
$\frac{- R }{ n ^2}+ R =\frac{1}{\lambda} $
$R -\frac{1}{\lambda}=\frac{ R }{ n ^2}$
$ \frac{\lambda R -1}{\lambda}=\frac{ R }{ n ^2} $
$ n ^2=\frac{\lambda R }{\lambda R -1} \Rightarrow n =\sqrt{\frac{\lambda R }{\lambda R -1}}$
Answer: 100
Solution
$ \frac{d v}{d s}=5$
$ a=v \frac{d v}{d s}=20 \times 5=100 \,m / sec ^2$
Answer: 2
Solution

$ \vec{ r }_{ com }=\frac{ M (0 \hat{ i }+0 \hat{ j })+ M (3 \hat{ i })+ M (3 \hat{ j })}{3 M } $
$ \vec{ r }_{ com }=\hat{ i }+\hat{ j }$
$ \left|\vec{ r }_{ com }\right|=\sqrt{2}=\sqrt{ x } $
$ x =2$
Answer: 90
Solution
Energy released by water $=0.3 \times 25 \times 4200=31500 J$
let $m kg$ ice melts
$m \times 3.5 \times 10^5=31500$
$m =\frac{31500 \times 10^{-5}}{3.5}=9000 \times 10^{-5} $
$ m =0.09 \,kg =90 \,gm $
$x =90$
Answer: 5
Solution
$ \frac{13.6\left(\frac{1}{2^2}-\frac{1}{3^2}\right)}{13.6\left(\frac{1}{2^2}-0\right)}=\frac{x}{x+4} ; \frac{\frac{1}{4}-\frac{1}{9}}{\frac{1}{4}}=\frac{x}{x+4}$
$ \frac{5}{9}=\frac{x}{x+4} $
$ 5 x+20=9 x$
$ 4 x=20 $
$x=5$
Answer: 18
Solution
$ 1.2=$( Potential Gradient )$ \times 36$
$ 1.8=$( Potential Gradient ) $\times x$
On dividing, we get
$\frac{2}{3} =\frac{36}{x} $
$x =18 \times 3=54\, cm$
Hence difference $=54-36=18\, cm$
Answer: 25
Solution

The forward biased diode will conduct while the reverse biased will not
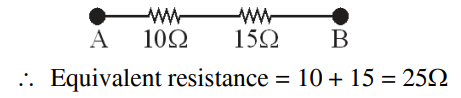
Answer: 60
Solution
$ A _{\text {resultant }}=\sqrt{ A _1^2+ A _2^2+2 A _1 A _2 \cos \phi} $
$\Rightarrow \sqrt{3} A =\sqrt{ A ^2+ A ^2+2 A ^2 \cos \phi} $
$ \Rightarrow 3 A ^2=2 A ^2+2 A ^2 \cos \phi$
$ \Rightarrow \cos \phi=\frac{1}{2}$
$ \therefore \phi=60^{\circ} $
$ \therefore $ Phase difference $=60 $ degree
Answer: 6
Solution

Initial charge on $C =18\, CV$
initial charge on $3 C =54 \,CV$
Let final common potential difference $= V ^{\prime}$
$9\, CV ^{\prime}+3 \,CV ^{\prime}=18 \,CV +54 \,CV$
$\Rightarrow 12\, CV ^{\prime}=72 \,CV \Rightarrow V ^{\prime}=6\, V$
Answer: 10
Solution

For lens
$ \frac{1}{ v }-\frac{1}{ u }=\frac{1}{ f } $
$\Rightarrow \frac{1}{ v }-\frac{1}{(-60)}=\frac{1}{20} \Rightarrow \frac{1}{ v }+\frac{1}{60}=\frac{1}{20}$
$ v =30 \,cm$
For final image to be formed on the object itself, after refraction from lens the ray should meet the mirror perpendicularly and the image by lens should be on the centre of curvature of mirror
$R =30-10=20\, cm$
Focal length of mirror $= R / 2=10 c\,m$
Answer: 250
Solution
$ \phi=8 t^2-9 t+5$
$ e m f=-\frac{d \phi}{d t}=-(16 t-9)$
At $t =0.25 s$
$Emf =-[(16 \times 0.25)-9]=5 \,V$
Current $=\frac{\text { Emf }}{\text { Resistance }}=\frac{5 V }{20 \Omega}$
$=\frac{1}{4} A =\frac{1000}{4} mA =250\, mA$
JEE Main Chemistry Question Paper with Solution 2023 July 25th Shift 2 - Evening
A
A-II, B-I, C-IV, D-III
B
A-II, B-IV, C-III, D-I
C
A-IV, B-II, C-III, D-I
D
A-IV, B-II, C-I, D-III
Solution
A
$1: 4$
B
$1: 0.25$
C
$1: 0.20$
D
$1: 5$
Solution
$ \frac{\Delta T _{ fx }}{\Delta T _{ fy }}=\frac{ k _{ f } \cdot m _{ x }}{ k _{ f } \cdot m _{ y }}=\frac{\frac{1 / M _{ x }}{1}}{\frac{1 / M _{ y }}{1}} $
$ \Rightarrow \frac{1}{4}=\frac{ M _{ y }}{ M _{ x }} $
$ \Rightarrow M _{ x }: M _{ y }=1: 0.25$
A
$K _{ a _3}= K _{ a _1}+ K _{ a _2}$
B
$K _{ a _3}= K _{ a _1}- K _{ a _2}$
C
$K _{ a _3}= K _{ a _1} / K _{ a _2}$
D
$K _{ a _3}= K _{ a _1} \times K _{ a _2}$
Solution
$ H _2 C _2 O _4 \rightleftharpoons H ^{+}+ HC _2 O _4^{-} K _{ a _1} $
$ H _2 C _2 O _4^{-} \rightleftharpoons H ^{+}+ C _2 O _4^{2-} K _{ a _2} $
$ H _2 C _2 O _4 \rightleftharpoons 2 H ^{+}+ C _2 O _4^{2-} K _{ a _3}= K _{ a _1} \times K _{ a _2} $
A
$\Lambda_{ m 2}=2 \Lambda_{ m 1}$
B
$\Lambda_{ m 2}=\Lambda_{ m 1} / 2$
C
$\Lambda_{ m 2}=\Lambda_{ m 1}$
D
$\Lambda_{ m 2}=4 \Lambda_{ m 1}$
Solution
$ \Lambda_{ m }=\kappa \times \frac{1000}{ M } $
$ \Rightarrow \Lambda_{ m } \propto \frac{1}{ M }$
$ \frac{\Lambda_{ m _1}}{\Lambda_{ m _2}}=\frac{ M _2}{ M _1}=\frac{\frac{20}{80}}{\frac{10}{20}}=\frac{1}{4} \times \frac{2}{1}=\frac{1}{2} $
$\Rightarrow \Lambda_{ m _2}=2 \Lambda_{ m _1}$
A
A and D only
B
A and C only
C
B and C only
D
B and D only
Solution
For micelle formation, $\Delta S >0$ (hydrophobic effect) This is possible because, the decrease in entropy due to clustering is offset by increase in entropy due to desolvation of the surfactant, Also $\Delta H >0$
A
$O < N < B < Be$
B
$Be < B < N < O$
C
$B < Be < N < O$
D
$B < Be < O < N$
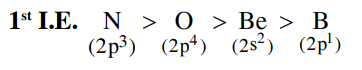
A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are not correct.
C
Statement I is correct but Statement II is not correct
D
Statement I is not correct but Statement II is correct.
Solution
Statement $- I$ is incorrect because cast iron is obtained by heating pig iron with scrap iron Statement-II is also incorrect because pig iron has more carbon content $(\sim 4 \%)$ than cast $\operatorname{iron}(\sim 3 \%)$
A
reaction of zinc with aqueous alkali.
B
electrolysis of acidified water using platinum electrodes.
C
electrolysis of warm aqueous barium hydroxide solution between nickel electrodes.
D
reaction of zinc with dilute acid.
Solution
High purity $(>99.95 \%)$ dihydrogen is obtained by electrolysis of warm aqueous $Ba ( OH )_2$ solution between $Ni$-electrodes
A
$Be > Mg > Ca > Sr$
B
$Sr > Ca > Mg > Be$
C
$Sr > Be > Mg > Ca$
D
$Be > Sr > Mg > Ca$
Solution
In II'A' group density decreases down the group till $Ca$ and after that it increases. Correct order of density is
$Sr > Be > Mg > Ca$
A
3
B
4
C
5
D
6
Solution
Neutral Oxides $- N _2 O , NO , CO$
Acidic Oxides - $B _2 O _3, N _2 O _5, SO _3, P _4 O _{10}$
A
$C < B < A$
B
$B < C < A$
C
$C < A < B$
D
$A < C < B$
Solution
Stronger the ligand, larger the splitting & higher the energy of absorption.
$\underset{(A)}{[Ni(en)_3]^{+2}} > \underset{(B)}{[Ni(NH_3)_6]^{+2}} > \underset{(C)}{[Ni(H_2O)_6]^{+2}}$
A
A-II, B-III. C-IV, D-I
B
A-IV, B-III, C-II, D-I
C
A-III, B-II, C-I, D-IV
D
A-III, B-II, C-IV, D-I
Solution
A-Sulphate - III (Laxative effect)
B-Fluoride - II (Bending of bones)
C-Nictoine - I (pesticides)
D-Sodium Arsinite - IV (herbicide)
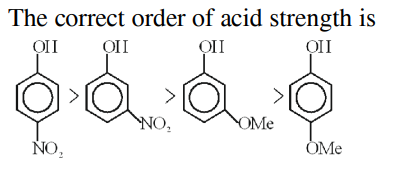
A
A > B > C > D
B
B > A > C > D
C
D > C > A > B
D
D > C > B > A
A
$CH_3 - CH_2 - CH_2 - CH_3$
B
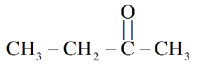
C
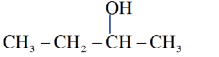
D
$CH_3 - CH_2 - CH = CH_2$
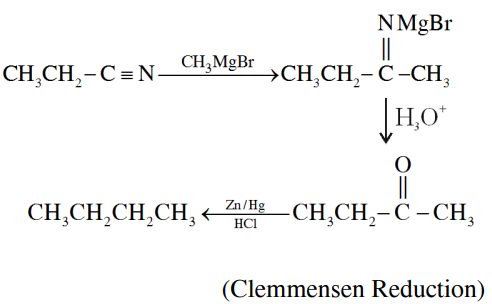
A
A-III, B-I, C-IV, D-II
B
A-III, B-IV, C-I, D-II
C
A-II, B-I, C-IV, D-III
D
A-II, B-IV, C-I, D-III
Solution
LDPE $\rightarrow$ Toys
HDPE $\rightarrow$ Buckets
Q18. Glycosidic linkage between $C _1$ of $\alpha$-glucose and $C_2$ of $\beta$-fructose is found in
A
maltose
B
sucrose
C
lactose
D
amylose
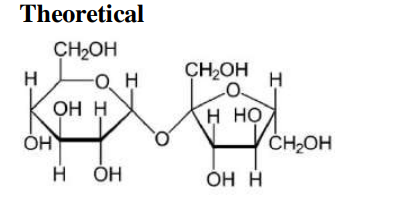
A
non-active site
B
allosteric site
C
competitive site
D
therapeutic site
Solution
Theoretical
A
quinonoid form
B
heterocyclic form
C
phenolic form
D
benzenoid form
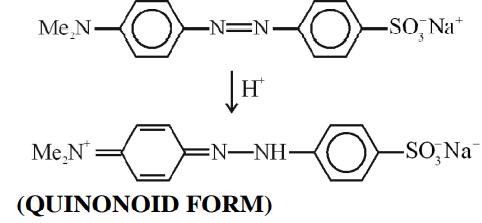
Answer: 1655
Solution
Moles of $C _3 H _8=\frac{11}{44}=0.25$ moles
$ PV = nRT$
$ \Rightarrow 2 \times 10^6 \times 2 \times 10^{-3}=0.25 \times 8.3 \times T$
$ \Rightarrow T =1927.710 \,K =1654.56^{\circ} C$
Answer: 4
Solution
Since only a single $H$ atom is present, maximum number of spectral lines $= 4$
Answer: 2
Solution
$ \Delta H _{\text {ionisation }} \text { of } CH _3 COOH =|-57.3-(-55.3)| $
$ =2 \,KJ / mol $
Answer: 2
Solution
For first order reaction
$ k =\frac{1}{ t } \ln \left(\frac{ P _0}{ P }\right) $
$ \ln \left(\frac{ P _0}{ P }\right)= kt$
$ t _{1 / 2}=\frac{\ln 2}{ k }=\frac{0.693}{3.465 \times 10^4}=2 \times 10^{-5}$
Answer: 4
Solution
$ \left. E _{ Cr ^{+3}}^0\right|_{ Cr ^{+2}}=-0.41 V$
$ {\left[ Cr ^{+3}\right]=4 s ^0 3 d ^3}$
$ \mu = \sqrt{ n ( n +2)} \text { B.M }$
$=\sqrt{15} \text { B.M } \sim 4 \text { B.M }$
Answer: 33
Solution
$ROH + CH _3 MgI \rightarrow ROMgI + CH _4( g )$
moles of $CH _4=$ moles of $ROH$
$\Rightarrow \frac{ V }{22400}=\frac{ m }{ M . M } $ (Assuming NTP Condition)
$ \Rightarrow \frac{3.1}{22400}=\frac{4.5 \times 10^{-3}}{ M . M} $
$\Rightarrow MM =32.51$
Nearest Integer $=33$
Answer: 2
Solution
$\frac{ R _{ F _{ A }}}{ R _{ F _{ B }}}=\frac{\frac{2.08}{3.25}}{\frac{1.05}{3.25}}=\frac{2.08}{1.05} \simeq 2$
Answer: 8
Solution
The Alkanes and their mono bromo dervative are
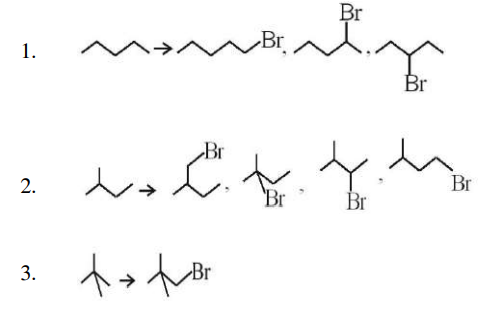
JEE Main Mathematics Question Paper with Solution 2023 July 25th Shift 2 - Evening
A
3
B
$\frac{7}{2}$
C
4
D
$\frac{9}{2}$
Solution

$ \sqrt{(3 \sqrt{2})^2+( p \sqrt{2})^2}=5 \sqrt{2}$
$18+2 p ^2=50$
$ p ^2=16 $
$p =\pm 4$
As per option $( C )$ is correct
A
0
B
1
C
2
D
4
Solution
$ 2 x-3 y+5 z=9 $
$ x+3 y-z=-18$
$ 3 x-y+\left(\lambda^2-|\lambda|\right) z=16$
$ D = \begin{vmatrix} 2 & -3 & 5 \\1 & 3 & -1 \\3 & -1 & \lambda^2-\mid \lambda\end{vmatrix}=0$
$ \Rightarrow 3 \lambda^2-3|\lambda|-11=0$
Clearly one negative and one positive root since $|\lambda|$ is there so negative not possible and two values of $\lambda$ corresponding to positive value
$D _3= \begin{vmatrix} 2 & -3 & 9 \\1 & 3 & -18 \\3 & -1 & 16\end{vmatrix} \neq 0 $ so no solution.
A
${ }^{50} P _{17}$
B
${ }^{50} P _{33}$
C
$33 ! \times 17 !$
D
$\frac{50 \text { ! }}{2}$
Solution
$ f :\{1,3,5,7, \ldots . .99\} \rightarrow\{2,4,6,8, \ldots ., 100\} $
$ f (3) \geq f (9) \geq f (15) \geq \ldots \ldots . f (99) \ldots . . \text { (1) } $
$ 3,9,15, \ldots . .99 \Rightarrow 17 $ numbers
for condition one we have ${ }^{50} C _{17} \times 1$ way rest $33$ elements $33 !$
$={ }^{50} C _{17} \times 33 ! $
$ ={ }^{50} C _{33} \times 33 ! $
$ ={ }^{50} P _{33} .$
A
$\frac{7}{87}$
B
$\frac{7}{29}$
C
$\frac{14}{87}$
D
$\frac{21}{29}$
Solution
$ \displaystyle\sum_{n=1}^{21} \frac{3}{(4 n-1)(4 n+3)} $
$ =\frac{3}{4} \displaystyle\sum_{n=1}^{21} \frac{(4 n+3)-(4 n-1)}{(4 n-1)(4 n+3)} $
$=\frac{3}{4} \displaystyle\sum_{n=1}^{21} \frac{1}{4 n-1}-\frac{1}{4 n+3}$
$ =\frac{3}{4}\left(\frac{1}{3}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+\frac{1}{11}-\ldots .+\frac{1}{83}-\frac{1}{87}\right) $
$ =\frac{3}{4}\left(\frac{1}{3}-\frac{1}{87}\right)=\frac{7}{29}$
A
14
B
7
C
$14 \sqrt{2}$
D
$7 \sqrt{2}$
Solution
$ \sin x+\cos x=t $
$ 1+\sin 2 x=t^2$
$ \sin 2 x=t^2-1 $
$ \displaystyle\lim _{t \rightarrow \sqrt{2}} \frac{8 \sqrt{2}-t^7}{\sqrt{2}-\sqrt{2}\left(t^2-1\right)} $
$ \displaystyle\lim _{t \rightarrow \sqrt{2}} \frac{8 \sqrt{2}-t^7}{2 \sqrt{2}-\sqrt{2} t^2} \text { (L-Hospital Rule) }$
$ \displaystyle\lim _{t \rightarrow \sqrt{2}} \frac{-7 t^6}{-2 \sqrt{2} t}=\displaystyle\lim _{t \rightarrow \sqrt{2}} \frac{7}{2 \sqrt{2}} \times t^5 $
$ =\frac{7}{2 \sqrt{2}} \times(\sqrt{2})^5=14$
A
$\frac{1}{2}$
B
1
C
2
D
$-2$
Solution
$\displaystyle \lim _{n \rightarrow \infty} \frac{1}{2^n} \displaystyle\sum_{r=1}^{2^n} \frac{1}{\sqrt{1-\frac{r}{2^n}}}$
$\therefore \frac{1}{2^n} \rightarrow d x \Leftarrow \frac{r}{2^n}=x \left(\frac{r}{n^{\prime}}=x, \frac{1}{x}=d x\right) $
$ 2^n=n^{\prime}$
$ \displaystyle\lim _{n^{\prime} \rightarrow \infty} \frac{1}{n^{\prime}} \displaystyle\sum_{r=1}^{n^{\prime}-1} \frac{1}{\sqrt{1-\frac{r}{n^{\prime}}}}=\int\limits_0^1 \frac{1}{\sqrt{1-x}} d x $
$ \left.=-\frac{(1-x)^{1 / 2}}{1 / 2}\right]_0^1=-2[0-1]=2$
A
$\frac{3}{4}$
B
$\frac{5}{8}$
C
$\frac{5}{4}$
D
$\frac{7}{8}$
Solution
$ P ( A \cup B )= P ( A )+ P ( B )- P ( A \cap B ) $
$ \frac{1}{2}=\frac{1}{3}+\frac{1}{5}- P ( A \cap B ) $
$ P ( A \cap B )=\frac{1}{30}$
$ P \left(\frac{ A }{\overline{ B }}\right)+ P \left(\frac{ B }{\overline{ A }}\right)=\frac{ P ( A \cap \overline{ B })}{ P (\overline{ B })}+\frac{ P ( B \cap \overline{ A })}{ P (\overline{ A })}$
$ =\frac{ P ( A )- P \left( A \cap B ^{\prime}\right)}{1- P ( B )}+\frac{ P ( B )- P ( A \cap B )}{1- P ( A )} $
$ =\frac{\frac{1}{3}-\frac{1}{30}}{\frac{4}{5}}+\frac{\frac{1}{5}-\frac{1}{30}}{\frac{2}{3}}=\frac{5}{8}$
A
$\frac{52(1- e )}{ e }$
B
$\frac{52}{ e }$
C
$\frac{52(2+ e )}{ e }$
D
$\frac{104}{ e }$
Solution
$ \int\limits_{-3}^{101}\left([\sin \pi x ]+ e ^{[\cos 2 \pi x ]}\right) dx $
$ 52 \int\limits_0^2\left([\sin \pi x ]+ e ^{[\cos 2 \pi x ]}\right) dt$
$ \frac{52}{\pi} \int\limits_0^{2 \pi}\left([\sin t ]+ e ^{[\cos 2 t]}\right) dt$
$\frac{52}{\pi} \int\limits_0^{2 \pi}\left([\sin t ] dt +\int\limits_0^{2 \pi} e ^{[\cos 2 t]} dt \right)$
$I_1=\int\limits_0^{2 \pi}[\sin t] d t$
Using King
$ I _1=\int\limits_0^{2 \pi}[-\sin t ] dt$
$2 I _1=\int\limits_0^{2 \pi}(-1) dt =-2 \pi$
$ I _1=-\pi $
$ I _2=2 \int\limits_0^\pi e ^{[\cos 2 t]} dt $
$=2.2 \int\limits_0^{\pi / 2} e ^{[\cos 2 t]} dt$
$ =4\left(\int\limits_0^{\pi / 4} e ^0 \cdot dt +\int\limits_{\pi / 4}^{\pi / 2} e ^{-1} dt \right) $
$ 4\left(\frac{\pi}{4}+ e ^{-1}\left(\frac{\pi}{4}\right)\right)=\pi\left(1+ e ^{-1}\right)$
$ I =\frac{52}{\pi}\left(-\pi+\pi+\pi e ^{-1}\right)=\frac{52}{ e }$
A
$-14$
B
42
C
$-22$
D
14
Solution

By observing origin and $P$ lies in same region.
$L _1(0,0)>0 ; L _1(\alpha, \beta)>0 \Rightarrow 3 \alpha-4 \beta+12>0$ $1=\left|\frac{3 \alpha-4 \beta+12}{5}\right|$
$3 \alpha-4 \beta+12=5......$(1)
Similarly for $L _2$
$L _2(0,0)>0 ; L _2(\alpha, \beta)>0$
$1=\left|\frac{8 \alpha+6 \beta+11}{10}\right| \Rightarrow 8 \alpha+6 \beta+11=10 .......$(2)
Solving (1) and (2)
$ \alpha=-\frac{23}{25} ; \beta=\frac{106}{100}$
$100(\alpha+\beta)=100\left(\frac{-92}{100}+\frac{106}{100}\right)=14$
A
$2 \log _{ e } 2$
B
4
C
1
D
$4 \log _{ e } 2$
Solution
$ \frac{d y}{d x}=-\frac{\alpha y}{x} $
$ \frac{d y}{y}=-\frac{\alpha}{x} d x $
$\Rightarrow \frac{d y}{y}+\frac{\alpha}{x} d x=0$
$ \Rightarrow \ell n y+\alpha \ell n x=\ell n c$
$ \Rightarrow yx^\alpha=c $
For $(1,2) \Rightarrow 2.1^\alpha=c \Rightarrow c=2$
For $(8,1) \Rightarrow 1.8^\alpha=2 \Rightarrow \alpha=\frac{1}{3}$
$\therefore$ curve is $y =2 x ^{-1 / 3}$
At $x=1 / 8, y(1 / 8)=2\left(\frac{1}{8}\right)^{-\frac{1}{3}} \Rightarrow y=4$
A
$\frac{5}{7}$
B
$\frac{2 \sqrt{6}}{7}$
C
$\frac{3}{7}$
D
$\frac{2 \sqrt{5}}{7}$
Solution
Ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ passes through the point $(7,0)$ and $(0,-2 \sqrt{6})$
Now $\frac{49}{ a ^2}+0=1 \Rightarrow a ^2=49$
and $0+\frac{24}{ b ^2}=1 \Rightarrow b ^2=24$
Now $a > b \Rightarrow b ^2= a ^2\left(1- e ^2\right)$
$\Rightarrow 24=49\left(1- e ^2\right) \Rightarrow e ^2=\frac{25}{49} \Rightarrow e =\frac{5}{7}$
A
4
B
6
C
7
D
8
Solution
Both point $A (1,3), B (1,-1)$ lies on the parabola
$y^2-2 y-2 x-1=0$
Fquation of tangent aty $A(1,3)$ is $T=0$
$x-2 y+5=0$
and equation of tangent at $B (1,-1)$ is $T =0$
$x +2 y +1=0$
So point $P$ is $(-3,1)$
$\Rightarrow A =\frac{1}{2} \begin{vmatrix}1 & 3 & 1 \\1 & -1 & 1 \\-3 & 1 & 1\end{vmatrix}=8$
A
$\frac{32}{9}$
B
$\frac{18}{5}$
C
$\frac{27}{4}$
D
$\frac{27}{10}$
Solution
$\frac{x^2}{16}+\frac{y^2}{7}=1 $
$\Rightarrow 7=16\left(1- e ^2\right) \Rightarrow e =\frac{3}{4}$
Foci of ellipse is $(\pm a e, 0) \Rightarrow(\pm 3,0)$
Now hyperbola be $\frac{x^2}{144}-\frac{y^2}{\alpha}=\frac{1}{25}$
$\frac{x^2}{\frac{144}{25}}-\frac{y^2}{\frac{\alpha}{25}}=1$
Now $a =\frac{12}{5}, b ^2=\frac{\alpha}{25}$
Let eccentricity of hyperbola be e ae $=3$ (Given)
$ \Rightarrow \frac{12}{5} e =3 \Rightarrow e =\frac{5}{4} $
$b ^2= a ^2\left( e ^2-1\right)$
$\frac{\alpha}{25}=\frac{144}{25}\left(\frac{25}{16}-1\right) \Rightarrow \alpha=81$
Hyperbola is $\frac{x^2}{\frac{144}{25}}-\frac{y^2}{\frac{81}{25}}=1$
Now length of $L R=\frac{2 b^2}{a}=\frac{27}{10}$
A
9
B
12
C
21
D
33
Solution
Let equation of plane be $a ( x -1)+ b ( y +1)+ c ( z -1)=0$.....(1)
It is perpendicular to the given two planes
$ 2 a-2 b+c=0$
$ a-b+2 c=0$
$\Rightarrow \frac{a}{3}=\frac{b}{3}=\frac{c}{0}$
Equation of plane be $x + y =0$
Now $\frac{| a + a |}{\sqrt{2}}=3 \sqrt{2} \Rightarrow|2 a |=6 \Rightarrow a =\pm 3$
$P (3,3,2)$ or $P (-3,-3,2), Q (1,-1,1)$
$PQ ^2=(3-1)^2+(3+1)^2+(2-1)^2=21$
A
$2 \sqrt{29}$
B
1
C
$\sqrt{\frac{37}{29}}$
D
$\frac{\sqrt{29}}{2}$
Solution
$ \frac{x+7}{-6}=\frac{y-6}{7}=\frac{z-0}{1}:$
point $(-7,6,0) \text { dr's }-6,7,1 $
$ \frac{x-7}{2}=\frac{y-2}{-1}=\frac{z-6}{-1}: $
point $(7,2,6) \text { dr's } 2,-1,-1$
Shortest distance
$=\left|\frac{ \begin{vmatrix} 14 & -4 & 6 \\-6 & 7 & 1 \\2 & -1 & -1\end{vmatrix}}{\sqrt{(-7+1)^2+(6-2)^2+(6-14)^2}}\right|=2 \sqrt{29}$
A
$\frac{2}{\sqrt{21}}$
B
$2 \sqrt{\frac{3}{7}}$
C
$\frac{2}{3} \sqrt{\frac{7}{3}}$
D
$\frac{2}{3}$
Solution
Projection of $\vec{b}$ on vector $\vec{a}-\vec{b}$ is
$ =\frac{\vec{ b } \cdot(\vec{ a }-\vec{ b })}{|\vec{ a }-\vec{ b }|} $
$ =\frac{\vec{ a } \cdot \vec{ b }-| b |^2}{\sqrt{ a ^2+ b ^2-2 a \cdot b }}=\frac{3- b ^2}{\sqrt{6+ b ^2-6}}=\frac{3- b ^2}{ b }$
$ |\vec{ a } \times \vec{ b }|^2=5 $
$ a ^2 b ^2-( a \cdot b )^2=5$
$ 6 b ^2=14 \Rightarrow b ^2=\frac{7}{3} $
$ \therefore \frac{3- b ^2}{ b }=\frac{3-\frac{7}{3}}{\sqrt{\frac{7}{3}}}=2 \times \sqrt{21}$
A
$11.5$
B
$10.5$
C
12
D
11
Solution
$ 3,5,7,2 k , 12,16,21,24 $
Median $=\frac{2 k +12}{2}= k +6$
M.D. $=\frac{\Sigma\left| x _{ i }- M \right|}{8}=6 $
$=( k +3)+( k +1)+( k -1)+(6- k )+(6- $
$k )+(10- k )+(15- k )+(18- k )=48$
$ =58-2 k =48 $
$ k =5$
Median $= k +6=11$
A
$\frac{3}{16}$
B
$\frac{1}{16}$
C
$\frac{1}{32}$
D
$\frac{9}{32}$
Solution
$2 \sin \left(\frac{\pi}{22}\right) \sin \left(\frac{3 \pi}{22}\right) \sin \left(\frac{5 \pi}{22}\right) \sin \left(\frac{7 \pi}{22}\right) \sin \left(\frac{9 \pi}{22}\right)$
$2 \cos \left(\frac{\pi}{2}-\frac{\pi}{22}\right) \cos \left(\frac{\pi}{2}-\frac{3 \pi}{22}\right) \cos \left(\frac{\pi}{2}-\frac{5 \pi}{22}\right) \cos \left(\frac{\pi}{2}-\frac{7 \pi}{15}\right) $
$ \cos \left(\frac{\pi}{2}-\frac{9 \pi}{22}\right)$
$2 \cos \left(\frac{10 \pi}{22}\right) \cos \left(\frac{8 \pi}{22}\right) \cos \left(\frac{6 \pi}{22}\right) \cos \left(\frac{4 \pi}{22}\right) \cos \left(\frac{2 \pi}{22}\right)$
$ 2 \cos \left(\frac{\pi}{11}\right) \cos \left(\frac{2 \pi}{11}\right) \cos \left(\frac{3 \pi}{11}\right) \cos \left(\frac{4 \pi}{11}\right) \cos \left(\frac{5 \pi}{11}\right)$
$ 2 \cos \left(\frac{\pi}{11}\right) \cos \left(\frac{2 \pi}{11}\right) \cos \left(\frac{4 \pi}{11}\right) \cos \left(\pi-\frac{3 \pi}{11}\right) \cos \left(\pi+\frac{5 \pi}{11}\right) $
$2 \cos \left(\frac{\pi}{11}\right) \cos \left(\frac{2 \pi}{11}\right) \cos \left(\frac{4 \pi}{11}\right) \cos \left(\frac{8 \pi}{11}\right) \cos \left(\frac{16 \pi}{11}\right)$
$ \frac{2 \cdot \sin \left(2^5 \times \frac{\pi}{11}\right)}{2^5 \sin \frac{\pi}{11}} $
$ \frac{2 \cdot \sin \left(\frac{32 \pi}{11}\right)}{32 \sin \frac{\pi}{11}}=\frac{1}{16}$
A
$(( P \wedge(\sim R )) \wedge Q ) \wedge((\sim Q ) \wedge((\sim P ) \vee R ))$
B
$(( P \wedge R ) \wedge Q ) \vee((\sim Q ) \wedge((\sim P ) \vee(\sim R )))$
C
$(( P \wedge R ) \wedge Q ) \wedge((\sim Q ) \wedge((\sim P ) \vee(\sim R )))$
D
$(( P \wedge(\sim R )) \wedge Q ) \vee((\sim Q ) \wedge((\sim P ) \vee R ))$
Solution
Negation of $( P \wedge \sim R ) \leftrightarrow(\sim Q )$
$\Rightarrow(( P \wedge \sim R ) \wedge Q ) \vee(\sim Q \wedge \sim( P \wedge \sim R ))$
$ \Rightarrow(( P \wedge \sim R ) \wedge Q ) \vee(\sim Q \wedge(\sim P \vee R ))$
Answer $D$ is correct
Answer: 107
Solution
$A :\{1,2,3,4,5,6,7\}$
Number of elements in set B
$= n (1 \notin T )+ n (2 \in T )- n [(1 \notin T ) \cap(2 \in T )] $
$=2^6+2^6-2^5=96$
Number of elements in set $C$
$ =\{\{2\},\{3\},\{5\},\{7\},\{1,2\},\{1,4\},\{1,6\}, $
$ \{2,3\},\{2,5\},\{3,4\},\{4,7\},\{5,6\},\{6,7\} $
$ \{1,2,4\},\{1,3,7\},\{1,4,6\},\{1,5,7\},\{2,3, $
$ 6\},\{2,4,5\},\{2,4,7\},\{2,5,6\},\{3,4,6\}, $
$\{4,6,7\},\{1,2,4,6\},\{2,4,6,7\},\{2,4,6, $
$ 5\},\{3,5,7,4\},\{1,3,5,4\},\{1,5,7,4\},\{1, $
$ 2,3,5\},\{1,2,3,7\},\{1,3,6,7\},\{1,5,6,7\}, $
$ \{2,3,5,7\},\{1,5,7,2,4\},\{3,5,7,2,6\},\{1,$
$ 3, 7, 2, 4\}, \{1,4, 5, 6, 7\}, $
$ \{1,3,4,5,6\},\{1,2,3,6,7\},\{1,2,3,5,6\}, $
$ \{1,2,3,4,6,7\} $
Number of elementrrs in $C =42$
$ \Rightarrow n(B \cup C)=n(B)+n(C)-n(B \cap C) $
$ =96+42-31=107$
Answer: 25
Solution
Let $f( x )= x ^2+ bx + p$
$f (1)=\frac{1}{3} \Rightarrow 1+ b + p =\frac{1}{3} .....$(1)
Assume common root be $\alpha$
$ f (\alpha)=0 \& f(f(f(f(\alpha))))=0 $
$ \Rightarrow f ( f ( f (0)))=0 $
$ \Rightarrow f ( f ( p ))=0 $
$\Rightarrow f \left( p ^2+ bp + p \right)=0 $
$ \Rightarrow f ( p ( p + b +1))=0 $
$ \Rightarrow f \left(\frac{ p }{3}\right)=0$
$ \Rightarrow \frac{p^2}{9}+b \cdot \frac{p}{3}+p=0$
$ \Rightarrow \frac{p}{9}+\frac{b}{3}+1=0$
$ p+3 b+9=0.....$(2)
From (1) & (2) $\Rightarrow p =\frac{7}{2}$
Now, $f(-3)=9-3 b+p$
$=9-(-p-9)+p $
$ =18+2 p =18+2 \times \frac{7}{2}=25$
Answer: 24
Solution
$ A^2 = \begin{bmatrix} 1 & a & a \\ 0 & 1 & b \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & a & a \\ 0 & 1 & b \\ 0 & 0 & 1\end{bmatrix} $
$ =\begin{bmatrix} 1 & 2 a & 2 a+a b \\ 0 & 1 & 2 b \\ 0 & 0 & 1\end{bmatrix} $
$ A^2 A = \begin{bmatrix} 0 & 1 & 2 b \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 0 & 1 & b \\ 0 & 0 & 1\end{bmatrix} $
$ A ^3 = \begin{bmatrix} 1 & 3 a & 3 a+3 a b \\ 0 & 1 & 3 b \\ 0 & 0 & 1\end{bmatrix}$
$A ^4= \begin{bmatrix} 1 & 4 a & 4 a +6 ab \\ 0 & 1 & 4 b \\ 0 & 1 & 1\end{bmatrix} $
$ A ^{ n }= \begin{bmatrix} 1 & \text { na } & \frac{\left( n ^2- n \right)}{2} ab + na \\ 0 & 1 & nb \\ 0 & 0 & 1\end{bmatrix} $
$ na =48, nb =96$
$ na +\frac{ nab }{2}( n -1)=2160$
$ 48+24 b ( n -1)=2160 $
$ 48+24 \times 96-24 b =2160 $
$ b =8 and a =4, n =12 $
$ n + a + b =24$
Answer: 15
Solution
Graph of $x^2+2 x$

Graph of $| 5x - 7|$

$\left. f ( x )\right|_{\min }=4+0=4$, at $x=\frac{7}{5}$
$\left. f ( x )\right|_{\max }=8+3=11$, at $x =2$
Required sum $=15$
Answer: 3
Solution
$ \frac{d y}{d x}=\frac{4 y^3+2 y x^2}{3 x y^2+x^3}, y(1)=1 $
$ \frac{d y}{d x}=\frac{4(y / x)^3+2(y / x)}{3(y / x)^2+1} $
$ y=x p $
$ x \frac{d p}{d x}+p=\frac{4 p^3+2 p}{3 p^2+1} $
$ x \frac{d p}{d x}=\frac{p^3+p}{3 p^2+1} $
$ \int \frac{3 p^2+1}{p^3+p} d p=\int \frac{d x}{x} $
$ \ln \left(p^3+p\right)=\ln x+\ln C $
$ p^3+p=x C$
$\left(\frac{ y }{ x }\right)^3+\left(\frac{ y }{ x }\right)= xC$
$ y ^3+ x ^2 y = x ^4 C $
$x =1, y =1 $
$ 1+1= C \Rightarrow C =2 $
$ y ^3+ x ^2 y =2 x ^4 $
Put $ x=2 $
$ y ^3+4 y -32=0$
Having root between $2$ and $3$
$y(2) \in[2,3)$
Answer: 8
Solution
$f ^{\prime}(0)=4$
$f(x)+\int\limits_0^x(x-t) f^{\prime}(t) d t=\left(e^{2 x}+e^{-2 x}\right) \cos 2 x+\frac{2}{a} x$
Put $x=0: f(0)=2$
$ f ^{\prime}(x)+x\left(f^{\prime}(x)\right)+\int\limits_0^x f^{\prime}(t) d t-x f^{\prime}(x) $
$ =\left(e^{2 x}+e^{-2 x}\right)(-2 \sin 2 x) $
$ +\cos 2 x\left(2 e^{2 x}-2 e^{-2 x}\right)+\frac{2}{a} $
$ \Rightarrow f^{\prime}(x)+f(x)-2=\left(e^{2 x}+e^{-2 x}\right)(-2 \sin 2 x) $
$ +\cos 2 x\left(2 e^{2 x}-2 e^{-2 x}\right)+\frac{2}{a}$
Put $x =0$
$4+2-2=0+(2-2)+2 / a$
$ \Rightarrow a =\frac{1}{2} $
$ (2 a +1)^5 a ^2=2^5 \cdot \frac{1}{2^2}=8$
Answer: 5
Solution
$ \int\limits_{-1}^{ n }\left(1+\frac{ x }{2}+\frac{ x ^2}{3}+\ldots+\frac{ x ^{ n -1}}{ n }\right) dx $
${\left[ x +\frac{ x ^2}{2}+\frac{ x ^3}{3^2}+\ldots+\frac{ x ^{ n }}{ n ^2}\right]_{-1}^{ n }} $
$\left( n +\frac{ n ^2}{2^2}+\frac{ n ^3}{3^2}+\ldots+-\frac{ n ^{ n }}{ n ^2}\right) $
$ -\left(-1+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{4^2}+\ldots+\frac{(-1)^{ n }}{ n ^2}\right) $
$ a _{ n }=( n +1)+\frac{1}{2^2}\left( n ^2-1\right)+\frac{1}{3^2}\left( n ^3+1\right) $
$+\ldots+\frac{1}{ n ^2}\left( n ^{ n }-(-1)^{ n }\right)$
if $ n =1 \Rightarrow a _{ n }=2 \notin(2,30)$
if $n =2 $
$ \Rightarrow a _{ n }=(2+1)+\frac{1}{2^2}\left(2^2-1\right)=3+\frac{3}{4}< 30 $
if $ n =3 $
$ \Rightarrow a _{ n }=(3+1)+\frac{1}{4}(8)+\frac{1}{9}(28)=11+\frac{28}{9}< 30$
If $ n =4 $
$ \Rightarrow a _{ n }=(4+1)+\frac{1}{4}(16-1)+\frac{1}{9}(64+1)+\frac{1}{16} $
$ =5+\frac{15}{4}+\frac{65}{9}+\frac{255}{16}>30$
Test $\{2,3\}$ sum of elements 5
Answer: 25
Solution
$ C _1(-3,-4) $
$ r _1=\sqrt{25-16}=3 $
$ C _2=(-3+\sqrt{3},-4+\sqrt{6}) $
$ r _2=\sqrt{34+ k } $
$ C _1 C _2=\left| r _1- r _2\right|$
$ C _1 C _2=\sqrt{3+6}=3$
$ 3=|3-\sqrt{34+ k }| \Rightarrow k =2 $
$ r _2=6$

$ (\alpha, \beta)=(-\sqrt{3}-3,-4-\sqrt{6}) $
$ (\alpha+\sqrt{3})^2+(\beta+\sqrt{6})^2=9+16=25$
Answer: 170
Solution
$ 4 x^3-3 x y^2+6 x^2-5 x y-8 y^2+9 x+14=0 $ at $ P(-2,3)$
$ 12 x^2-3\left(y^2+2 y x y^{\prime}\right)+12 x-5\left(x y^{\prime}+y\right)-16 y y^{\prime}+ 9=0$
$ 48-3\left(9-12 y^{\prime}\right)-24-5\left(-2 y^{\prime}+3\right)-48 y^{\prime}+9 =0$
$ y^{\prime}=-9 / 2 $
Tangent $y-3=-\frac{9}{2}(x+2) \Rightarrow 9 x+2 y=-12$
Normal $: y-3=\frac{2}{9}(x+2) \Rightarrow 9 y-2 x=31$

Area $=\frac{1}{2}\left(\frac{31}{2}-4\right) \times 3=\frac{85}{4}$
$ 8 A =170$
Answer: 130




















