JEE Main Question Paper with Solution 2023 January 30th Shift 2 - Evening

A

A-IV, B-I, C-III, D-II

B

A-I, B-IV, C-III, D-II

C

A-IV, B-III, C-I, D-II

D

A-IV, B-I, C-II, D-III

A

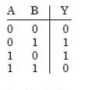
B

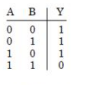
C

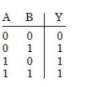
D

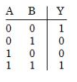
Solution

Given circuit represent $XOR$.

A

Both $A$ and $R$ are true and $R$ is the correct explanation of $A$

B

$A$ is false but $R$ is true

C

Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$

D

A is true but $R$ is false

Solution

Nuclear density is independent of $A$.

A

$E_I=0, E_{I I}=0, E_{I I I}=0$

B

$E_I \neq 0, E_{I I}=0, E_{I I}=0$

C

$E_I=0, E_{I I}=0, E_{I I I} \neq 0$

D

$E_I \neq 0, E_{I I}=0, E_{I I I} \neq 0$

Solution

Electric field inside material of conductor is zero.

A

$\sqrt{g R}$

B

$2 \sqrt{g R}$

C

$\sqrt{2 g R}$

D

$\sqrt{\frac{g R}{2}}$

Solution

Loss in PE = Gain in KE
$ \left(-\frac{ GMm }{2 R }\right)-\left(-\frac{ GMm }{ R }\right)=\frac{1}{2} mv ^2 $
$ \Rightarrow v ^2=\frac{ GM }{ R }= gR$
$ \Rightarrow v =\sqrt{ gR }$

A

$\sqrt{2}$

B

$1 / 2$

C

2

D

$1 / \sqrt{2}$

Solution

$ \omega=\sqrt{\frac{ k }{ m }} $
$ \frac{\omega_2}{\omega_1}=\sqrt{\frac{ m _1}{ m _2}}=\sqrt{\frac{1}{2}}$

A

$2.77 \times 10^{-2} mm$

B

$6.9 \times 10^{-2} mm$

C

$6.06 \times 10^{-2} mm$

D

$3.0 \times 10^{-2} mm$

Solution

$ Y =\frac{ F / A }{\frac{\Delta \ell}{\ell}} $
$ \Rightarrow F =\frac{ YA }{\ell} \Delta \ell $
$ \left(\frac{ A \Delta \ell}{\ell}\right)_1=\left(\frac{ A \Delta \ell}{\ell}\right)_2 $
$ \Rightarrow \frac{\Delta \ell_2}{\Delta \ell_1}=\frac{ A _1}{ A _2} \times \frac{\ell_2}{\ell_1} $
$ \Rightarrow \frac{\Delta \ell_2}{0.2}=\frac{1}{2.4 \times 2.4} \times \frac{2}{1} $
$\Rightarrow \Delta \ell_2=6.9 \times 10^{-2} mm$

A

$0.6\, m / s$

B

$2.5\, m / s$

C

$1.5 \,m / s$

D

$0.02\, m / s$

Solution

$ 20 \times 10^{-3} \times \frac{180}{60} \times 100=10\, V $
$ \Rightarrow v =0.6 \,m / s $

A

$1: 5$

B

$1: 3$

C

$1: 2$

D

$1: 4$

Solution

$F \propto I _1 I _2$
$F _1: F _{2 I }=1: 4$

A

$2: 1$

B

$1: 4$

C

$1: 1$

D

$4: 1$

Solution

$ K _{ av }=\frac{5}{2} kT $
Ratio $=1: 1$

A

$4 \sqrt{3} \times 10^{-4} T$

B

$\sqrt{3} \times 10^{-4} T$

C

$4 \sqrt{3} \times 10^{-5} T$

D

$3 \sqrt{3} \times 10^{-5} T$

Solution

$d \tan 60^{\circ}=2 \sqrt{3} $
$ d =2 \,cm $
$ B =3 \times \frac{\mu_0 i }{2 \pi d } \sin 60^{\circ} $
$ =3 \times \frac{2 \times 10^{-7} \times 2}{2 \times 10^{-2}} \times \frac{\sqrt{3}}{2}$
$ =3 \sqrt{3} \times 10^{-5}$

A

$25 \,N$

B

$15\, N$

C

$10 \,N$

D

$20 \,N$

Solution

$ \theta=30^{\circ} $
$ \cos \theta=\frac{\sqrt{3} g}{ T } $
$ \Rightarrow \frac{\sqrt{3}}{2}=\frac{\sqrt{3} g}{ T } $
$ \Rightarrow T =20\,N $

A

$\frac{2}{3} \Omega$

B

$\frac{3}{2} \Omega$

C

$\frac{1}{3} \Omega$

D

$\frac{1}{2} \Omega$

Solution

$\frac{1}{ R _{ eq }} =\frac{1}{2}+\frac{1}{12}+\frac{1}{4}+\frac{1}{6}+\frac{1}{2}$
$ =\frac{6+1+3+2+6}{12}=\frac{18}{12}=\frac{3}{2} $
$ \Rightarrow R _{ eq }=\frac{2}{3} \Omega$

A

$A$ is true but $R$ is false

B

Both $A$ and $R$ are true and $R$ is the correct explanation of $A$

C

Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$

D

A is false but $R$ is true

Solution

Both A and R are true and R is the correct explanation of A

A

4

B

$\frac{9}{4}$

C

3

D

$\frac{3}{2}$

Solution

$ KE =\frac{ P ^2}{2 m }, $
$P =\frac{ h }{\lambda} $
$ eV _1=\frac{\left(\frac{ h }{\lambda}\right)^2}{2 m } $
$ eV _2=\frac{\left(\frac{ h }{1.5 \lambda}\right)^2}{2 m } $
$ \frac{ V _1}{ V _2}=(1.5)^2=\frac{9}{4}$

A

A-II, B-III, C-IV, D-I

B

A-IV, B-III, C-II, D-I

C

A-I, B-II, C-III, D-IV

D

A-IV, B-III, C-I, D-II

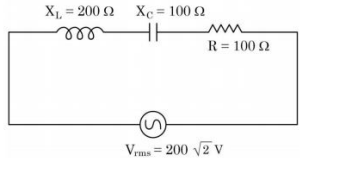
A

$\frac{1}{2} A$

B

$20 A$

C

$2 A$

D

$2 \sqrt{2} A$

Solution

$ z =\sqrt{100^2+(200-100)^2} $
$ =100 \sqrt{2} \Omega $
$ i _{ rms }=\frac{ V _{ rms }}{ z }=\frac{200 \sqrt{2}}{100 \sqrt{2}} $
$ =2 A$

A

$3.75\, km / h$

B

$4.25\, km / h$

C

$3.50 \, km / h$

D

$4.00\, km / h$

Solution

$ \frac{2}{ V _{ av }}=\frac{1}{3}+\frac{1}{5}=\frac{8}{15} $
$ \Rightarrow V _{ av }=\frac{15}{4}=3.75\, km / h $

A

$7.8^{\circ}$

B

$4.5^{\circ}$

C

$6^{\ circ}$

D

$1.3^{\circ}$

Solution

$ \delta_1= \delta_2 $ [for no average deviation]
$ \Rightarrow 6^{\circ}(1.54-1)= A (1.72-1) $
$ \Rightarrow A =\frac{6^{\circ} \times 0.54}{0.72} $
$=\frac{18^{\circ}}{4}=4.5^{\circ}$

A

$\frac{1}{40 \pi} \frac{W}{m^2}$

B

$\frac{1}{10 \pi} \frac{W}{m^2}$

C

$\frac{1}{20 \pi} \frac{W}{m^2}$

D

$\frac{1}{2 \pi} \frac{W}{m^2}$

Solution

$I _{ EF }=\frac{1}{2} \times \frac{5}{4 \pi \times 5^2} $
$ =\frac{1}{40 \pi} W / m ^2$

Solution

$ \vec{ E }=2 x ^2 \hat{ i }-4 y \hat{ j }+6 \hat{ k } $

$\phi_{\text {net }}=-8 \times 3+2 \times 6=-12$
$ -12=\frac{ q }{\epsilon_0} $
$ | q |=12 \epsilon_0$

Solution

$a =-\mu_{ k } g =-3 $
$ V =18-3 \times 2 $
$ V =12\, m / s $
$ KE =\frac{1}{2} mv ^2+\frac{1}{2} \frac{ mr ^2}{2} \frac{ v ^2}{ r ^2}$
$KE =\frac{3}{4} mv ^2$
$ KE =3 \times 18=54\, J $

Solution

$ \frac{41^{\circ}-5^{\circ}}{95^{\circ}-5^{\circ}}=\frac{ C -0^{\circ}}{100^{\circ}-0^{\circ}} $
$ \Rightarrow C =\frac{36}{90} \times 100=40^{\circ} C =313\, K $

Solution

$ \frac{1}{2} mV ^2= Pt $
$ V =\sqrt{\frac{2 Pt }{ m }} $
$ \frac{ dx }{ dt }=\sqrt{\frac{2 Pt }{ m }} $
$ x =\sqrt{\frac{2 P }{ m } \frac{2}{3}}\left[ t ^{3 / 2}\right]_0^4 $
$ x =\frac{16 \sqrt{ P }}{3}=\frac{1}{3} \times 16 \sqrt{ P }$
$ \alpha=4$

Solution

$\frac{2}{3}=\frac{\frac{x}{x+1}}{x} $
$ \Rightarrow \frac{2}{3}=\frac{1}{x+1} $
$\Rightarrow x=0.5=\frac{1}{2} $
$ n=2$

Solution

$a=\omega^2 R =\left(\frac{28 \times 2 \pi}{60}\right)^2 \times 1.8 $
$ =\left(\frac{56}{60} \times \frac{22}{7}\right)^2 \times 1.8 $
$ =\frac{(44)^2}{225} \times 1.8 $
$ =\frac{1936 \times 1.8}{225}$
$ x=125$

Solution

$ I =4 I _0 \cos ^2\left(\frac{\Delta \phi}{2}\right)$
$ I _1=4 I _0 \cos ^2\left(\frac{\pi}{4}\right)=2 I _0$
$ I _2=4 I _0 \cos ^2\left(\frac{2 \pi}{3}\right)= I _0 $
$ \Rightarrow \frac{ I _1+ I _2}{ I _0}=3$

Solution

$ \xi_{\max }= NAB \omega $
$ =100 \times 14 \times 10^{-2} \times 3 \times \frac{360 \times 2 \pi}{60} $
$=1584\, V $

Solution

$4 v ^2=50- x ^2 $
$ \Rightarrow v =\frac{1}{2} \sqrt{50- x ^2} $
$ \omega=\frac{1}{2} $
$ T =\frac{2 \pi}{\omega}=4 \pi=\frac{88}{7} $
$ x =88$

Solution

$\frac{ dN _1}{ dt }=-\lambda_1 N $
$\frac{ dN _2}{ dt }=-\lambda_2 N $
$ \frac{ dN }{ dt }=-\left(\lambda_1+\lambda_2\right) N $
$\Rightarrow \lambda_{ eq }=\lambda_1+\lambda_2 $
$ \Rightarrow \frac{1}{ t _{1 / 2}}=\frac{1}{300}+\frac{1}{30}=\frac{11}{300} $
$\Rightarrow t _{1 / 2}=\frac{300}{11}$

A

Strong hydrogen bond in Boric acid

B

Strong van der Waal's interaction in Boric acid

C

Strong covalent bond in $BF _3$

D

Strong ionic bond in Boric acid

Solution

Boric acid has strong hydrogen bonding while $BF_3$ does not. Therefore boric acid is solid

A

$180^{\circ}$

B

$90^{\circ}$

C

$90^{\circ} \& 180^{\circ}$

D

$90^{\circ} \& 120^{\circ}$

Solution

The $Cl - Co - Cl$ bond angle in above octahedral complex is $90^{\circ}$

A

$IO _3^{-} \& IO _3^{-}$

B

$I _2 \& IO _3^{-}$

C

$I _2 \& I _2$

D

$IO _3^{-} \& I _2$

Solution

In acidic medium
$2 MnO _4^{-}+10 I ^{-}+16 H ^{+} \rightarrow 2 Mn ^{2+}+5 I _2+8 H _2 O$
In neutral/faintly alkaline solution
$2 MnO _4^{-}+ I ^{-}+ H _2 O \rightarrow 2 MnO _2+2 OH ^{-}+ IO _3^{-}$

A

Water has high amount of fluoride compounds

B

Highly polluted water

C

Very clean water

D

Slightly polluted water

Solution

Clean water as BOD value of $< 5 $ while polluted water has BOD of $15 $ or more.

A

$a>b>c>d$

B

$b > a > d > c$

C

$b > d > a > c$

D

$c > a > d > b$

Solution

Due to $- M$ effect of $- NO _2$ group, it increases acidity $+ M$ effect of $N \left( CH _3\right)_2$ decreases acidity.
Hyperconjugation of isopropyl decrease acidity
$\therefore$ order of acidic strength
(c) $>$ (a) $>$ (d) $>$ (b)

A

A is false but $R$ is true

B

Both $A$ and $R$ are true and $R$ is the correct explanation of $A$

C

A is true but $R$ is false

D

Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$

Solution

Antiallergic and antacid drugs work on different receptors

A

A is false but $R$ is true

B

Both A and $R$ are true but $R$ is not the correct explanation of $A$

C

A is true but $R$ is false

D

Both A and R are true and $R$ is the correct explanation of $A$

Solution

The acid sensitive alcohol group reacts with $HCl, $ hence Clemmenson reduction is not suitable for above conversion.

A

Both Statement I and Statement II are correct

B

Both Statement I and Statement II are incorrect

C

Statement I is correct but Statement II is incorrect

D

Statement I is incorrect but Statement II is correct

Solution

In Electrolytic refining, the pure metal is used as cathode and impure metal is used as anode.
$Na _3 AlF _6$ is added during electrolysis of $Al _2 O _3$ to lower the melting point and increase conductivity.

A

c

B

d

C

b

D

a

Solution

The $+M$ effect of $NH_2$ is stabilizing the carbocation

A

$d>b>c>a$

B

$b > d > c > a$

C

$a > c > d > b$

D

$a > b > c > d$

Solution

The rate of $S_N1$ reaction depends upon stability of carbocation which follows the order

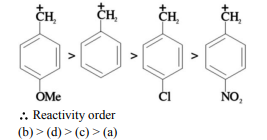
A

$D > C > B > A$

B

$B > A > C > D$

C

$A>B>D>C$

D

$A>B>C>D$

Solution

Bond dissociation energy of E-H bond in hydrides of group 16 follows the order
$ H _2 O > H _2 S > H _2 Se > H _2 Te $

A

72

B

16

C

32

D

50

Solution

The number of electrons in the orbitals of sub-shell of $n = 4 $ are

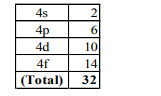
A

(i) $Fe , H ^{+}$ (ii)$ Br _2( aq ) $ (iii) $ HNO _2$ (iv) $CuBr$

B

(i) $Fe , H ^{+}$ (ii) $Br _2( aq )$ (iii) $HNO _2$ (iv) $H _3 PO _2$

C

(i) $Br _2, Fe$ (ii) $Fe , H ^{+}$ (iii) $LiAIH _4$

D

(i) $Br _2( aq )$ (ii) $LiAIH _4$ (iii) $H _3 O ^{+}$

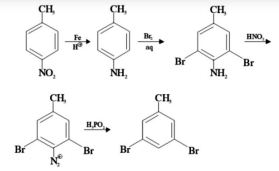
A

A-I, B-II, C-III, D-IV

B

A-II, B-I, C-III, D-IV

C

A-I, B-II, C-IV, D-III

D

A-II, B-I, C-IV, D-III

Solution

For $\left[ Fe \left( NH _3\right)_6\right]^{+2}, \Delta_0< P$, hence the pairing of electrons does not occur in $t _{2 g }$. Therefore complex is outer orbital and its hybridisation is $sp ^3 d ^2$.
Match List I with List II

List I (Complexes)	List II (Hybridisation)
$ [Ni(CO)_4]$	$sp^{3}$
$ [Cu(NH_{3})_{4}]^{2+} $	$dsp ^{2} $
$ [Fe(NH_{3})_{6}]^{2+} $	$ sp^{3}d^2 $
$ [Fe(H_{2}O)_{6}]^{2+} $	$sp^{3} d^2$

A

A-IV, B-I, C-III, D-II

B

A-III, B-IV, C-I, D-II

C

A-II, B-I, C-III, D-IV

D

A-III, B-I, C-IV, D-II

Solution

List I (Mixture)	List II (Separation Technique)
$CHCl_3 + C_6H_5NH_2$	Distillation
$C_6H_{14} + C_5H_{12}$	Fractional distillation
$C_6H_5NH_2 + H_2O$	Steam distillation
Organic compound in $H_2O$	Differential extraction

A

$KHgI _3$

B

$HgI _2$

C

$K _2 HgI _4$

D

$KHg _2 I _2$

Solution

Nessler's reagent is $K _2 HgI _4$.

A

$0.02,0.02$

B

$0.02,0.01$

C

$0.01,0.01$

D

$0.01,0.02$

A

$r_0=\frac{a_0}{2}$

B

$r_0=2 a_0$

C

$r_0=4 a_0$

D

$r_0=a_0$

Solution

At node $\Psi_{2 s}=0$
$ \therefore 2-\frac{r_0}{a_0}=0 $
$\therefore r_0=2 a_0$

A

$2 LiNO _3 \xrightarrow{\Delta} 2 NaNO _2+ O _2$

B

$4 LiNO _3 \xrightarrow{\Delta} 2 Li _2 O +2 N _2 O _4+ O _2$

C

$2 LiNO _3 \longrightarrow 2 Li +2 NO _2+ O _2$

D

$4 LiNO _3 \xrightarrow{\Delta} 2 Li _2 O +4 NO _2+ O _2$

Solution

$4 LiNO _3 \stackrel{ A }{\longrightarrow} 2 Li _2 O +4 NO _2+ O _2$

A

$Mg$

B

$Ca$

C

$K$

D

$Be$

Solution

$BeCl_2$ having covalent nature is soluble in organic solvent

Solution

$\text { Molarity }=\frac{50}{11.35}$
$\therefore$ Strength in $gm / L =\frac{50}{11.35} \times 34$

Solution

$ \Delta T _{ f }= i . K _{ f } \cdot m $
$ \Rightarrow \Delta T _{ f }=2.67 \times 1.8 \times \frac{38}{98} \times \frac{1000}{62} $
$ \Rightarrow \Delta T _{ f }=30.05 $
$ \therefore F . P .=243\, K$

Solution

$ X + Y ^{2+} \rightarrow Y + X ^{2+} $
$ E _{\text{ Cell} }^0=0.36-(-2.36)=2.72 V $
$ E _{\text {Cell }}=2.72-\frac{0.06}{2} \log \frac{0.001}{0.01} $
$ =2.72+0.03=2.75 V$
$ =275 \times 10^{-2} V $

Solution

$ \log \frac{x}{m}=\log k +\frac{1}{n} \log P $
$ \frac{1}{ n }=\tan 45^{\circ}=1 $
$ \log k =0.6020=\log 4 $
$ \Rightarrow K =4 $
$ \therefore \frac{ x }{ m }= K \cdot P ^{1 / n } $
$ \frac{ x }{ m }=4(0.4)=1.6 $
$ \frac{ x }{ m }=1.6=16 \times 10^{-1}$

Solution

$\frac{ t _1}{ t _2}=\frac{\frac{1}{ K } \ln \frac{ a _0}{0.4 a _0}}{\frac{1}{ K } \ln \frac{ a _0}{0.1 a _0}}$
$ \frac{540}{ t _2}=\frac{\ln \frac{10}{4}}{\ln 10} $
$\frac{540}{ t _2}=\frac{\log 10-\log 4}{\log 10}$
$ \frac{540}{ t _2}=\frac{1-0.6}{1} $
$ \Rightarrow \frac{540}{ t _2}=0.4 $
$ \Rightarrow t _2=\frac{540}{0.4}=1350 \sec$

Solution

$ q =0 $
$\Delta U = w $
$ 1 \times 20 \times\left[ T _2-300\right]=-3000 $
$ T _2-300=-150 $
$ T _2=150 \,K $

Solution

The yield of $SO _3$ at equilibrium will be due to :
B. Increasing pressure
C. Adding more $SO _2$
D. Adding more $O _2$

Solution

Number of peptide linkage = (amino acid - 1)
$ = 7 - 1 = 6 $

Solution

Compound $2, 3, 7$

Solution

$d =\frac{ Z \times M }{ N _0 \times a ^3} $
$ 4=\frac{ Z \times 72}{6 \times 10^{23} \times 125 \times 10^{-24}}$
$Z=4.166 \simeq 4$

A

$[x]$ is even but $[y]$ is odd

B

$[x]+[y]$ is even

C

$[x]$ and $[y]$ are both odd

D

$[x]$ is odd but $[y]$ is even

Solution

$x=(8 \sqrt{3}+13)={ }^{13} C_0 \cdot(8 \sqrt{3})^{13}+{ }^{13} C_1(8 \sqrt{3})^{12}(13)^1+\ldots$
$ x^{\prime}=(8 \sqrt{3}-13)^{13}={ }^{13} C_0(8 \sqrt{3})^{13} - {}^{13} C_1(8 \sqrt{3})^{12}(13)^1+\ldots $
$ x-x^{\prime}=2\left[{ }^{13} C_1 \cdot(8 \sqrt{3})^{12}(13)^1+{ }^{13} C_3(8 \sqrt{3})^{10} \cdot(13)^3 \ldots\right]$
therefore, $x-x^{\prime}$ is even integer, hence $[x]$ is even
$ \text { Now, } y =(7 \sqrt{2}+9)^9={ }^9 C _0(7 \sqrt{2})^9+{ }^9 C _1(7 \sqrt{2})^8(9)^1 +{ }^9 C _2(7 \sqrt{2})^7(9)^2 \ldots \ldots $
$y ^{\prime}=(7 \sqrt{2}-9)^9={ }^9 C _0(7 \sqrt{2})^9-{ }^9 C _1(7 \sqrt{2})^8(9)^1 +{ }^9 C _2(7 \sqrt{2})^7(9)^2 \ldots \ldots $
$ y - y ^{\prime}=2\left[{ }^9 C _1(7 \sqrt{2})^8(9)^1+{ }^9 C _3(7 \sqrt{2})^6(9)^3+\ldots\right] $
$ y - y ^{\prime}=$ Even integer, hence $[ y ] $ is even

A

$\sqrt{2} a-b+c=1$

B

$a+\sqrt{2} b+c=1$

C

$\sqrt{2} a+b+c=1$

D

$a+b+\sqrt{2} c=1$

Solution

$ \hat{ v }=\cos 60^{\circ} \hat{ i }+\cos 45^{\circ} \hat{ j }+\cos \gamma \hat{ k }$
$ \Rightarrow \frac{1}{4}+\frac{1}{2}+\cos ^2 \gamma=1 \quad(\gamma \rightarrow \text { Acute }) $
$\Rightarrow \cos \gamma=\frac{1}{2} $
$ \Rightarrow \gamma=60^{\circ}$
Equation of plane is
$ \frac{1}{2}(x-\sqrt{2})+\frac{1}{\sqrt{2}}(y+1)+\frac{1}{2}(z-1)=0$
$ \Rightarrow x+\sqrt{2} y+z=1$
$(a, b, c)$ lies on it.
$\Rightarrow a+\sqrt{2} b+c=1$

A

$|Adj P| >1$

B

$|A d j P|=\frac{1}{2}$

C

$P$ is a singular matrix

D

$|A d j P|=1$

Solution

$ P ^{ T }= aP +( a -1) I $
$ \Rightarrow P =a P ^{ T }+( a -1) I $
$ \Rightarrow P ^{ T }- P = a \left( P - P ^{ T }\right) $
$ \Rightarrow P = P ^{ T }, \text { as } a \neq-1 $
$ \text { Now, } P = aP +( a -1) I $
$ \Rightarrow P =- I \Rightarrow| P |=1 $
$ \Rightarrow|\text{Adj} P |=1$

A

164

B

243

C

$\frac{125}{3}$

D

25

Solution

$ x^2-p x+\frac{5 p}{4}=0 $
$ D=p^2-5 p=p(p-5) $
$ \therefore q=9 $
$ 0 \leq y \leq(x-9)^2$

Area $=\int\limits_0^9(x-9)^2 dx =243$

A

1

B

0

C

$\sin (1)$

D

$-1$

Solution

$ LHL =\displaystyle\lim _{ k \rightarrow 0} g ( h (- k )) , k >0 $
$=\displaystyle\lim _{ k \rightarrow 0} g (-2+1) $
$ \because f ( x )=-1 \forall x <0 $
$ = g (-1)=1 $
$ RHL =\displaystyle\lim _{ k \rightarrow 0} g ( h ( k )) , k >0 $
$ =\displaystyle\lim _{ k \rightarrow 0} g (-1) ,$
$ \because f ( x )=1, \forall x >0 $
$ =1$

A

$\cot ^{-1}(2022)-\frac{\pi}{4}$

B

$\frac{\pi}{4}-\cot ^{-1}(2022)$

C

$\tan ^{-1}(2022)-\frac{\pi}{4}$

D

$\frac{\pi}{4}-\tan ^{-1}(2022)$

Solution

$a _2- a _1= a _3- a _2=\ldots . .= a _{2022}- a _{2021}=1$.
$ \therefore \tan ^{-1}\left(\frac{ a _2- a _1}{1+ a _1 a _2}\right)+\tan ^{-1}\left(\frac{ a _3- a _2}{1+ a _2 a _3}\right)+\ldots . .+\tan ^{-1}\left(\frac{ a _{2022}- a _{2021}}{1+ a _{2021} a _{2022}}\right)$
$=\left[\left(\tan ^{-1} a_2\right)-\tan ^{-1} a_1\right]+\left[\tan ^{-1} a_3-\tan ^{-1} a_2\right]+\ldots . . +\left[\tan ^{-1} a _{2022}-\tan ^{-1} a _{2021}\right] $
$ =\tan ^{-1} a _{2022}-\tan ^{-1} a _1 $
$=\tan ^{-1}(2022)-\tan ^{-1} 1=\tan ^{-1} 2022-\frac{\pi}{4} \text { (option 3) } $
$ =\left(\frac{\pi}{2}-\cot ^{-1}(2022)\right)-\frac{\pi}{4}$
$ =\frac{\pi}{4}-\cot ^{-1}(2022)(\text { option 1) }$

A

$\frac{13}{6}$

B

$\frac{5}{17}$

C

$\frac{17}{5}$

D

$\frac{6}{13}$

Solution

$ \frac{x-1}{1}=\frac{2 y+1}{2}=\frac{z+1}{-1} $
$ \frac{x-1}{1}=\frac{y+\frac{1}{2}}{1}=\frac{z+1}{-1} $
$ \text { Points : } A(-1, k , 0), B (2, k ,-1), C (1,1,2) $
$ \overrightarrow{ CA }=-2 \hat{ i }+( k -1) \hat{ j }-2 \hat{ k } $
$\overrightarrow{ CB }=\hat{ i }+( k -1) \hat{ j }-3 \hat{ k }$
$\overrightarrow{ CA } \times \overrightarrow{ CB }=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ -2 & k -1 & -2 \\ 1 & k -1 & -3\end{vmatrix}$
$=\hat{ i }(-3 k +3+2 k -2)-\hat{ j }(6+2)+\hat{ k }(-2 k +2- k +1)$
$ =(1- k ) \hat{ i }-8 \hat{ j }+(3-3 k ) \hat{ k }$
The line $\frac{x-1}{1}=\frac{y+\frac{1}{2}}{1}=\frac{z+1}{-1}$ is perpendicular to normal vector.
$ \therefore 1 \cdot(1- k )+1(-8)+(-1)(3-3 k )=0$
$ \Rightarrow 1- k -8-3+3 k =0 $
$ \Rightarrow 2 k =10 \Rightarrow k =5 $
$ \therefore \frac{ k ^2+1}{( k -1)( k -2)}=\frac{26}{4 \cdot 3}=\frac{13}{6}$

A

$\frac{3}{2}$

B

3

C

6

D

4

Solution

$ f^{\prime}(x)=x^2+2 b+a x $
$ g^{\prime}(x)=x^2+a+2 b x $
$ (2 b-a)-x(2 b-a)=0 $
$ \therefore x=1 $ is the common root
Put $x=1 \text { in } f^{\prime}(x)=0 \text { or } g^{\prime}(x)=0 $
$ 1+2 b+a=0 $
$ 7+2 b+a=6$

A

$\frac{d}{a}, \frac{e}{b}, \frac{f}{c}$ are in G.P.

B

$d, e, f$ are in A.P.

C

$d, e, f$ are in G.P.

D

$\frac{d}{a}, \frac{e}{b}, \frac{f}{c}$ are in A.P.

Solution

$ ax ^2+2 bx + c =0 $
$ \Rightarrow ax ^2+2 \sqrt{ ac x}+ c =0\left(\because b ^2= ac \right) $
$\Rightarrow( x \sqrt{ a }+\sqrt{ c })^2=0 $
$ x ^2-\frac{\sqrt{ c }}{\sqrt{ a }} \ldots \ldots(1) $
$ \text { Now, } d x ^2+2 ex + f =0 $
$ \Rightarrow d \left(\frac{ c }{ a }\right)+2 e \left[-\frac{\sqrt{ c }}{\sqrt{ a }}\right]+ f =0 $
$ \Rightarrow \frac{d c}{ a }+ f =2 e \sqrt{\frac{ c }{ a }}$
$ \Rightarrow \frac{ d }{ a }+\frac{ f }{ c }=2 e \sqrt{\frac{1}{ ac }} $
$ \Rightarrow \frac{ d }{ a }+\frac{ f }{ c }=\frac{2 e }{ b }[\text { as } b =\sqrt{ ae }]$
$ \therefore \frac{ d }{ a }, \frac{ e }{ b }, \frac{ f }{ c } \text { are in A.P. }$

A

$-60$

B

$-48$

C

$-84$

D

$-24$

Solution

$\vec{ c }=(2 \vec{ a } \times \vec{ b })-3 \vec{ b } $
$ \vec{ b } \cdot \vec{ c }=\vec{ b } \cdot(2 \vec{ a } \times \vec{ b })-3 \vec{ b } \cdot \vec{ b }$
$ =-3| b |^2 $
$ =-48$

A

$\frac{19}{3}$

B

12

C

0

D

19

Solution

$ \displaystyle\lim _{n \rightarrow \infty} \frac{3}{n} \displaystyle\sum_{r=0}^{n-1}\left(2+\frac{r}{n}\right)^2 $
$ =3 \int\limits_0^1(2+x)^2 d x=27-8=19$

A

343

B

216

C

$\frac{343}{8}$

D

$\frac{125}{8}$

Solution

As $a ^3, b ^3, c ^3$ be in A.P. $\rightarrow a ^3+ c ^3=2 b ^3$.... (1)
$\log _a^b, \log _c^a, \log _b^c$ are in G.P.
$ \therefore \frac{\log b }{\log a } \cdot \frac{\log c }{\log b }=\left(\frac{\log a }{\log c }\right)^2$
$ \therefore(\log a )^3=(\log c )^3 \Rightarrow a = c$......(2)
From (1) and (2)
$ a = b = c $
$T _1=\frac{ a +4 b + c }{3}=2 a ; d =\frac{ a -8 b + c }{10}=\frac{-6 a }{10}=\frac{-3}{5} a$
$ \therefore S _{20}=\frac{20}{2}\left[4 a +19\left(-\frac{3}{5} a \right)\right]$
$=10\left[\frac{20 a -57 a }{5}\right]$
$ =-74 a $
$ \therefore-74 a =-444 \Rightarrow a =6$
$ \therefore a b c=6^3=216$

A

$[2 \sqrt{2}, \sqrt{11}]$

B

$[\sqrt{5}, \sqrt{10}]$

C

$[\sqrt{5}, \sqrt{13}]$

D

$[\sqrt{2}, \sqrt{7}]$

Solution

$ y^2=3-x+2+x+2 \sqrt{(3-x)(2+x)}$
$ =5+2 \sqrt{6+x-x^2} $
$ y^2=5+2 \sqrt{\frac{25}{4}-\left(x-\frac{1}{2}\right)^2}$
$ y_{\max }=\sqrt{5+5}=\sqrt{10} $
$ y_{\min }=\sqrt{5}$

A

$\{99\}$

B

$\phi$

C

$N$

D

$\{9\}$

Solution

let $a_1$ be any natural number
$ a_1, a_1+1, a_1+2, \ldots ., a_1+99 \text { are values of } a_i{ }^{\prime} S$
$ \bar{x}=\frac{a_1+\left(a_1+1\right)+\left(a_1+2\right)+\ldots . .+a_1+99}{100} $
$ =\frac{100 a_1+(1+2+\ldots . .+99)}{100}=a_1+\frac{99 \times 100}{2 \times 100} $
$ =a_1+\frac{99}{2}$
Mean deviation about mean $=\frac{\displaystyle\sum_{ i =1}^{100}\left| x _{ i }-\overline{ x }\right|}{100}$
$=\frac{2\left(\frac{99}{2}+\frac{97}{2}+\frac{95}{2}+\ldots .+\frac{1}{2}\right)}{100} $
$=\frac{1+3+\ldots .+99}{100} $
$=\frac{\frac{50}{2}[1+99]}{100} $
$ =25$
So, it is true for every natural no. ' $a _1$ '

A

76

B

81

C

72

D

64

Solution

$ y = mx +\frac{4}{ m }$
$ \frac{\left|\frac{4}{ m }\right|}{\sqrt{1+ m ^2}}=2 \sqrt{2}$
$ \therefore m =\pm 1 $
$ y =\pm x \pm 4$ Point of contact on parabola
Let $m =1,\left(\frac{ a }{ m ^2}, \frac{2 a }{ m }\right)$
$R (4,8)$
Point of contact on circle $Q(-2,2)$
$\therefore( QR )^2=36+36=72$

A

$(P \vee Q) \wedge((\sim P) \vee R)$

B

$(P \vee \sim Q) \wedge(P \vee \sim R)$

C

$((\sim P) \vee \sim Q) \wedge((\sim P) \vee \sim R)$

D

$((\sim P) \vee \sim Q) \wedge((\sim P) \vee R)$

Solution

$ P \rightarrow(\sim Q \wedge R)$
$ \sim P \vee(-Q \wedge R) $
$ (-P \vee \sim Q) \wedge(-P \vee R)$

A

54

B

108

C

268

D

186

Solution

$a \in\{2,4,6,8,10, \ldots ., 100\} $
$b \in\{1,3,5,7,9, \ldots \ldots, 99\}$
Now, $a+b \in\{25,71,117,163\}$
(i) $a+b=25$, no. of ordered pairs (a, b) is 12
(ii) $a + b =71$, no. of ordered pairs (a, b) is 35
(iii) $a + b =117$, no. of ordered pairs (a, b) is 42
(iv) $a+b=163$, no. of ordered pairs (a, b) is 19
$\therefore$ total $=108$ pairs

A

$\log _e|x+y|-\frac{x y}{(x+y)^2}=0$

B

$\log _e|x+y|-\frac{2 x y}{(x+y)^2}=0$

C

$\log _e|x+y|+\frac{x y}{(x+y)^2}=0$

D

$\log _e|x+y|+\frac{2 x y}{(x+y)^2}=0$

Solution

Put $y=v x$
$ v+x \frac{d v}{d x}=-\left(\frac{1+3 v^2}{3+v^2}\right)$
$ x \frac{d v}{d x}=-\frac{(v+1)^3}{3+v^2} $
$ \frac{\left(3+v^2\right) d v}{(v+1)^3}+\frac{d x}{x}=0 $
$ \int \frac{4 d v}{(v+1)^3}+\int \frac{d v}{v+1}-\int \frac{2 d v}{(v+1)^2}+\int \frac{d x}{x}=0$
$ \frac{-2}{(v+1)^2}+\ln (v+1)+\frac{2}{v+1}+\ln x=c $
$ \frac{-2 x^2}{(x+y)^2}+\ln \left(\frac{x+y}{x}\right)+\frac{2 x}{x+y}+\ln x=c $
$\frac{2 x y}{(x+y)^2}+\ln (x+y)=c$
$ \therefore c=0, \text { as } x=1, y=0$
$\therefore \frac{2 x y}{(x+y)^2}+\ln (x+y)=0$

A

136

B

132

C

140

D

144

Solution

$ \vec{ a }=\lambda \hat{ i }+2 \hat{ j }-3 \hat{ k } $
$\vec{ b }=\hat{ i }-\lambda \hat{ j }+2 \hat{ k }$
$\Rightarrow(\vec{ b }-\vec{ a }) \times((\vec{ a }+\vec{ b }) \times(\vec{ a } \times \vec{ b }))=8 \hat{ i }-40 \hat{ j }-24 \hat{ k } $
$ \Rightarrow((\vec{ a }-\vec{ b }) \cdot(\vec{ a }+\vec{ b }))(\vec{ a } \times \vec{ b })=8 \hat{ i }-40 j -24 \hat{ k } $
$ \Rightarrow 8(\vec{ a } \times \vec{ b })=8 \hat{ i }-40 \hat{ j }-24 \hat{ k }$
Now, $\vec{a} \times \vec{b}=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ \lambda & 2 & -3 \\ 1 & -\lambda & 2\end{vmatrix}$
$ =(4-3 \lambda) \hat{ i }-(2 \lambda+3) \hat{ j }+\left(-\lambda^2-2\right) \hat{ k } $
$ \Rightarrow \lambda=1 $
$ \therefore \vec{ a }=\hat{ i }+2 \hat{ j }-3 \hat{ k } $
$\vec{ b }=\hat{ i }-\hat{ j }+2 \hat{ k }$
$ \Rightarrow \vec{ a }+\vec{ b }=2 \hat{ i }+\hat{ j }-\hat{ k }, \vec{ a }-\vec{ b }=3 \hat{ j }-5 \hat{ k }$
$\Rightarrow(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 2 & 1 & -1 \\ 0 & 3 & -5\end{vmatrix}=2 \hat{i}+10 \hat{ j }+6 \hat{ k }$
$\therefore$ required answer $=4+100+36=140$

A

$x^2-18 x+56=0$

B

$x^2+14 x+24=0$

C

$x^2-10 x+16=0$

D

$x^2+18 x+56=0$

Solution

$\begin{vmatrix}1 & -1 & 1 \\ 2 & 2 & \alpha \\ 3 & -1 & 4\end{vmatrix}=0 ; 8+\alpha-2(-4+1)+3(-\alpha-2)=0$
$ 8+\alpha+6-3 \alpha-6=0 $
$ \alpha=4$

Solution

$\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 1 & 3 & -2 \\ 1 & -1 & 2\end{vmatrix}=4 \hat{ i }-4 \hat{ j }-4 \hat{ k }$
$\therefore$ Equation of line is $\frac{ x -2}{1}=\frac{ y -3}{-1}=\frac{ z -1}{-1}$
Let $Q$ be $(5,3,8)$ and foot of $\perp$ from $Q$ on this line be $R$.
Now, $R \equiv( k +2,- k +3,- k +1)$
$DR$ of $QR$ are $( k -3,- k ,- k -7)$
$ \therefore(1)( k -3)+(-1)(- k )+(-1)(- k -7)=0 $
$ \Rightarrow k =-\frac{4}{3}$
$\therefore \alpha^2=\left(\frac{13}{3}\right)^2+\left(\frac{4}{3}\right)^2+\left(\frac{17}{3}\right)^2=\frac{474}{9}$
$ \therefore 3 \alpha^2=158$

Solution

$\frac{1}{2} \times PC \times \sqrt{5}=\frac{\sqrt{35}}{2} ; PC =\sqrt{7}$

$a _1^2+ b _1^2+ a _2^2+ b _2^2= OP ^2+ OQ ^2$
$ =2(5+7)=24$

Solution

$ T_8=11+(8-1) \times 20 $
$ =11+140=151$

Solution

$ x + y =12^{50}+18^{50}=(150-6)^{25}+(325-1)^{25}$
$ =25 K -\left(6^{25}+1\right)=25 K -\left((5+1)^{25}+1\right) $
$ =25 K _1-2 $
Remainder $=23$

Solution

$ p =\frac{{ }^6 C _1}{6 \times 6}=\frac{1}{6} $
$ q =\frac{{ }^6 C _1 \times{ }^5 C _1 \times 4}{6 \times 6 \times 6 \times 6}=\frac{5}{54} $
$ \therefore p : q =9: 5$
$ \Rightarrow m + n =14$

Solution

$ \int \sqrt{\sec 2 x-1} d x=\int \sqrt{\frac{1-\cos 2 x}{\cos 2 x}} d x $
$ =\sqrt{2} \int \frac{\sin x}{\sqrt{2 \cos ^2 x-1}} d x$
$ \text { put } \cos x=t \Rightarrow-\sin x d x=d t $
$ =-\sqrt{2} \int \frac{ dt }{\sqrt{2 t^2-1}} $
$=-\ln |\sqrt{2} \cos x+\sqrt{\cos 2 x}|+c $
$ =-\frac{1}{2} \ln \left|2 \cos { }^2 x+\cos 2 x+2 \sqrt{\cos 2 x} \cdot \sqrt{2} \cos x\right|+c $
$ =-\frac{1}{2} \ln \left|\cos 2 x+\frac{1}{2}+\sqrt{\cos 2 x} \cdot \sqrt{1+\cos 2 x}\right|+c $
$ \because \beta=\frac{1}{2}, \alpha=-\frac{1}{2} $
$\Rightarrow \beta-\alpha=1$

Solution

Digits are $1,2,2,2,3,3,5$
If unit digit 5 , then total numbers $=\frac{6 !}{3 ! 2 !}$
If unit digit 3 , then total numbers $=\frac{6 !}{3 !}$
If unit digit 1 , then total numbers $=\frac{6 !}{3 ! 2 !}$
$\therefore$ total numbers $=60+60+120=240$

Solution

$f(1)=1 ; f(9)=f(3) \times f(3)$
i.e., $f(3)=1$ or 3
Total function $=1 \times 6 \times 2 \times 6 \times 6 \times 1=432$

Solution

$ A =2 \int\limits_{\frac{1}{3}}^{\frac{1}{2}}\left(2 x-2 x ^2-(1- x )^2\right) dx $
$ =2\left[2 x ^2- x ^3- x \right]_{1 / 3}^{1 / 2} $
$ \therefore A =\frac{5}{108} \Rightarrow 540 A =\frac{5}{108} \times 540=25$

Solution

Two equations have common root
$ \therefore(4 a)(26 a)=(-6)^2=36 $
$ \Rightarrow a^2=\frac{9}{26} $
$ \therefore a=\frac{3}{\sqrt{26}}$
$\Rightarrow \beta=13$