JEE Main Physics Question Paper with Solution 2023 February 1st Shift 1 - Morning
A
$10 \,m / s$
B
$100\, m / s$
C
$200 \,\pi m / s$
D
$50\, m / s$
Solution
$v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{70}{70 \times 10^{-3}}}=100 \,m / s$
A
Bulk modulus
B
Compressibility
C
Modulus of rigidity
D
Energy density
Solution
$ {[b]=[V]} $
$ \left[\frac{a}{b^2}\right]=[P] $
$\therefore \left[\frac{b^2}{a}\right]=\frac{1}{[P]}=\frac{1}{[B]}=[K]$
A
$\frac{\mu_0 i}{2 r}\left(1+\frac{1}{\pi}\right)$
B
$\frac{\mu_0 i}{2 r}\left(1+\frac{2}{\pi}\right)$
C
$\frac{\mu_0 i}{2 r}\left(\frac{1}{2}+\frac{1}{\pi}\right)$
D
$\frac{\mu_0 i}{2 r}\left(\frac{1}{2}+\frac{1}{2 \pi}\right)$
Solution
$B_{ P }=\left(\frac{\mu_0 i}{4 r}+\frac{\mu_0 i}{4 \pi r}\right)=\frac{\mu_\theta i}{2 r}\left(\frac{1}{2}+\frac{1}{2 \pi}\right)$
A
$14.2 \, MeV$
B
$7.1 \, MeV$
C
$56.8\, MeV$
D
$28.4 \, MeV$
Solution
B.E of Helium $=\left(2 m_P+2 m_N-m_{H e}\right) c^2$
$=28.4 \,MeV$
A
A-IV, B-III, C-I, D-II
B
A-II, B-IV, C-I, D-III
C
A-II, B-I, C-III, D-IV
D
A-IV, B-II, C-I, D-III
A
$11 \frac{2}{3} R$
B
$14 R$
C
$\frac{8}{3} R$
D
$21 R$
Solution
Wheat stone bridge is in balanced condition

$ \frac{1}{R_{e q}}=\frac{1}{4 R}+\frac{1}{8 R} $
$ R_{e q}=\frac{8 R}{3}$
A
proportional to absolute temperature
B
proportional to volume
C
dependent on the nature of the gas
D
proportional to pressure
Solution
Basic theory
Translational $K . E$ on average of a molecule is $\frac{3}{2}$ $KT$ which is independent of nature, pressure and volume.
A
$\frac{\left(v_1+v_2+v_3\right)}{3}$
B
$\frac{3 v_1 v_2 v_3}{\left(v_1 v_2+v_2 v_3+v_3 v_1\right)}$
C
$\frac{\left(v_1+v_2+v_3\right)}{3 v_1 v_2 v_3}$
D
$\frac{v_1 v_2 v_3}{3\left(v_1 v_2+v_2 v_3+v_3 v_1\right)}$
Solution
$ AB =x $
$ BC =x $
$ 2 x+ CD =3 x$
$CD = x$
$\langle v \rangle=\frac{3 x}{\frac{x}{v_1}+\frac{x}{v_2}+\frac{x}{v_3}}=\frac{3 v_1 v_2 v_3}{v_2 v_3+v_1 v_3+v_1 v_2}$
A
A-I, B-II, C-III, D-IV
B
A-I, B-III, C-IV, D-II
C
A-IV, B-I, C-II, D-III
D
A-IV, B-III, C-II, D-I
A
6
B
5
C
3
D
4
Solution
After passing through first sheet
$I_1=\frac{I}{2}$
After passing through second sheet
$I_2=I_1 \cos ^2\left(45^{\circ}\right)=\frac{I}{4}$
After passing through $n^{\text {th }}$ sheet
$ I_{ n }=\frac{I}{2^{ n }}=\frac{I}{64} $
$ n=6$
A
$5 \times 10^{-5} J$
B
$17.5 \times 10^{-5} J$
C
$2.26 \times 10^{-5} J$
D
$28 \times 10^{-5} J$
Solution
Initial surface energy $=0.45 \times 4 \pi\left(10^{-3}\right)^2$
$ \frac{4}{3} \pi\left(10^{-3}\right)^3=125 \times \frac{4 \pi}{3} R_{\text {new }}^3$
$\therefore 10^{-3}=5 R_{\text {new }} $
$\therefore R_{\text {new }}=\frac{10^{-3}}{5} m$
So, final surface energy $=0.45 \times 125 \times 4 \pi\left(\frac{10^{-3}}{5}\right)^2$
Increase in energy $=0.45 \times 4 \pi \times\left(10^{-3}\right)^2\left[\frac{125}{25}-1\right]$
$=4 \times 0.45 \times 4 \pi \times 10^{-6}$
$=2.26 \times 10^{-5} J$
A
$2: 1$
B
$4: 1$
C
$1: 4$
D
$1: 2$
Solution
$K E=\frac{p^2}{2 m}=\frac{h^2}{2 m \lambda^2} $
$ \frac{K E_p}{K E_\alpha}=\frac{m_\alpha}{m_p}=4: 1$
A
A-I, B-II, C-III, D-IV
B
A-III, B-I, C-II, D-IV
C
A-II, B-I, C-III, D-IV
D
A-II, B-III, C-I, D-IV
A
$W=T R[\sqrt{2}-2]$
B
$W=\frac{R}{T}[2-\sqrt{2}]$
C
$W=R T[2-\sqrt{2}]$
D
$W=\frac{T}{R}[\sqrt{2}-2]$
Solution
$ T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}$
$ T V^{1 / 2}=T_2(2 V)^{1 / 2} $
$ T_2=\frac{T}{\sqrt{2}} $
$ W=\frac{R\left(T_1-T_2\right)}{\gamma-1}=\frac{R\left(T-\frac{T}{\sqrt{2}}\right)}{\frac{1}{2}}=R T(2-\sqrt{2})$
A
$64 \,MHz$
B
$106 \,MHz$
C
$99\, MHz$
D
$89 \,MHz$
Solution
FM broadcast range is 88MHz to 108MHz
A
Both Statement I and Statement II are false
B
Statement $I$ is false but Statement II is true
C
Statement I is true but Statement II is false
D
Both Statement I and Statement II are true
Solution
$g_{\text{eff}}=g-\omega^2 R_e \sin ^2 \theta, \theta \rightarrow$ co-latitude angle
$g_{\text {eff }}=g\left(1-\frac{d}{R_e}\right), d$ here depth
A
$\vec{E}_I=0, \vec{E}_{I I}=\frac{\sigma}{\epsilon_0} \hat{n}, E_{I I I}=0$
B
$\vec{E}_I=\frac{2 \sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{2 \sigma}{\epsilon_0} \hat{n}$
C
$\vec{E}_I=-\frac{\sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{\epsilon_0} \hat{n}$
D
$\vec{E}_I=\frac{\sigma}{2 \epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{2 \epsilon_0} \hat{n}$
Solution
Assuming RHS to be $\hat{n}$
$ \vec{E}_{ I }=\frac{\sigma}{2 \epsilon_0}(-\hat{n})+\frac{\sigma}{2 \epsilon_0}(-\hat{n})=-\frac{\sigma}{\epsilon_0} \hat{n} $
$ \vec{E}_{I I}=0 $
$ \vec{E}_{I I I}=\frac{\sigma}{2 \epsilon_0}(\hat{n})+\frac{\sigma}{2 \epsilon_0}(\hat{n})=\frac{\sigma}{\epsilon_0}(\hat{n})$
A
1
B
18
C
3
D
2
Solution
$v_{\text {(escape) plant }}=\sqrt{\frac{2 G M_P}{R_P}} $
$ =\sqrt{\frac{2 G\left(\frac{M_e}{9}\right)}{\left(\frac{R_e}{2}\right)}}=\frac{v_e \sqrt{2}}{3}$
$ \therefore x=2$
A
$0 .50$
B
$0.60$
C
$0.75$
D
$0.25$
Solution
$ S=u t+\frac{1}{2} a t^2 $
$ 50=0+\frac{1}{2} \times a \times 100 $
$ a=1 m / s ^2 $
$F-\mu m g=m a $
$ 30-\mu \times 50=5 \times 1$
$ 50 \mu=25 $
$ \mu=\frac{1}{2}$
Answer: 828
Solution
In the ground state energy $=-13.6 eV$
So energy
$ \frac{-13.6 eV }{n^2}=-13.6+12.75$
$ \frac{-13.6 eV }{n^2}=-0.85 $
$ n=\sqrt{16}$
$n=4$
Angular momentum $=\frac{n h}{2 \pi}=\frac{4 h}{2 \pi}=\frac{2 h}{\pi}$
Angular momentum $=\frac{2}{\pi} \times 4.14 \times 10^{-15}$
$=\frac{828 \times 10^{-17}}{\pi} eVs$
Answer: 2
Solution

$F=\frac{2 K q q_0 x}{\left(x^2+a^2\right)^{3 / 2}}$
For $F$ to be maximum
$\frac{ d F}{ d x}=0 $
$x=\frac{a}{\sqrt{2}}$
Answer: 25
Solution
$ \frac{E_1}{E_2}=\frac{l_1}{l_2} $
$ \frac{1.5}{E_2}=\frac{60}{60+40}=\frac{6}{10}=\frac{3}{5} $
$ E_2=\frac{5}{2}=\frac{x}{10} $
$ x=25$
Answer: 1
Solution
$ B_{\text {water }}=\frac{-\Delta P}{\left(\frac{\Delta V}{V}\right)}=\frac{-\Delta P}{\frac{0.01}{100}} $
$ B_{\text {liquid }}=\frac{-\Delta P}{\frac{0.03}{100}} $
$ \frac{B_{\text {water }}}{B_{\text {liquid }}}=3 $
$ x=1$
Answer: 2
Solution
$ K E=P E+\frac{P E}{4}$
$K E=\frac{5}{4} P E $
$ \frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{5}{4} \times \frac{1}{2} m \omega^2 x^2 $
$ {\left[ v =\omega \sqrt{ A ^2- x ^2}\right]} $
$ A^2-x^2=\frac{5}{4} x^2$
$ \frac{9 x^2}{4}=A^2$
$ x=\frac{2}{3} A $
$ \therefore x=\frac{2}{3} \times 3 cm$
$ x=2 \,cm $
Answer: 144
Solution
$r=\frac{m v}{q B}=\frac{\sqrt{2 k m}}{q B}, m=\frac{r^2 q^2 B^2}{2 k}$

$m =\frac{\frac{1}{100} \times \frac{3}{100} \times 2 \times 2 \times 4 \times 10^{-3} \times 4 \times 10^{-3} \times 10^{-12}}{2 \times(100) \times 10^{-6}}$
$=144 \times 10^{-18} kg$
Answer: 2
Solution
$v=\sqrt{\frac{2 g h}{1+\frac{k^2}{R^2}}}$
Where $h=60 \sin 30^{\circ}=30 cm$
$k^2=\frac{R^2}{2}$
$v=2\, ms ^{-1}$
Answer: 32
Solution

$U_A=-45 \,cm , f =-20 \,cm $
$ V_A=\frac{-45 \times(-20)}{-45-(-20)}=\frac{-900}{25}=-36 \,cm $
$ \text { And } U_B=-35 \,cm $
$ \therefore V_B=\frac{-35 \times(-20)}{-35-(-20)}=\frac{700}{-15}$
$ \therefore V_A-V_B=\text { length of image } $
$ =\left(-36+\frac{140}{3}\right)\, cm$
$ =\frac{-108+140}{3}\, cm $
$ =\frac{32}{3} \,cm $
$ \therefore x=32$
Answer: 40
Solution
To maximize the average rate at which energy supplied i.e. power will be maximum.
So in LCR circuit power will be maximum at the condition of resonance and in resonance condition
$X_L =X_C$
$79.6 =\frac{1}{\omega C}$
$\therefore C =\frac{1}{2 \pi \times 50 \times 79.6} $
$\therefore C =40 \mu F$
Answer: 40
Solution
$ W=\vec{F} \cdot\left(\vec{r}_f-\vec{r}_{ i }\right) $
$ =(5 \hat{i}+2 \hat{j}+7 \hat{k}) \cdot((5 \hat{i}-2 \hat{j}+\hat{k})-(2 \hat{i}+3 \hat{j}-4 \hat{k}))$
$ W=40 \,J$
JEE Main Chemistry Question Paper with Solution 2023 February 1st Shift 1 - Morning
A
$\left[ F _{ e }\left( C _2 O _4\right)_3\right]^{3-}$
B
$\left[ F _{ e }( CN )_6\right]^{3-}$
C
$\left[ F _{ e }\left( NH _3\right)_6\right]^{3+}$
D
$\left[ F _{ e } F _6\right]^{3-}$
Solution
$\overline{ C }N$ is a strong field ligand so maximum splitting in $d$ orbitals take place.
A
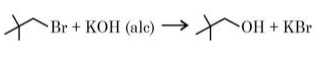
B
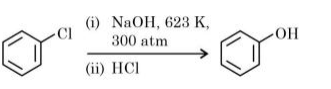
C

D
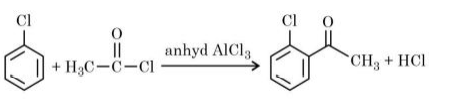
Solution
In alcoholic $KOH$, elimination reaction takes place.
A
(A) - III, (B) - IV, (C) - II, (D) - I
B
(A) - II, (B) - I, (C) - III, (D) - IV
C
(A) - III, (B) - IV, (C) - I, (D) - II
D
(A) - I, (B) - II, (C) - III, (D) - IV
Solution
List I Test
List II Functional group / Class of Compound
A
Molisch's Test
II
Carbohydrate
B
Biuret Test
I
Peptide
C
Carbylamine Test
III
Primary amine
D
Schiff s Test
IV
Aldehyde
| List I Test | List II Functional group / Class of Compound | ||
|---|---|---|---|
| A | Molisch's Test | II | Carbohydrate |
| B | Biuret Test | I | Peptide |
| C | Carbylamine Test | III | Primary amine |
| D | Schiff s Test | IV | Aldehyde |
A
$Fe \left[ Fe ( CN )_6\right]$
B
$K \left[ Fe _2( CN )_6\right]$
C
$Fe _4\left[ Fe ( CN )_6\right]_3$
D
$Fe _3\left[ Fe ( CN )_6\right]_2$
Solution
Formation of Prussian blue complex takes place
A
A and B only
B
A, B and D only
C
A and C only
D
B and D only
Solution
Double salt contain's two or more types of salts. $CuSO _4 \cdot 4 NH _3 \cdot H _2 O$ and $Fe ( CN )_2 .4 KCN$ are complex compounds.
A
$a>d>b>c$
B
$d > b > c > a$
C
$b > a > d > c$
D
$b>d>c>a$
Solution
Dehydration of alcohol is directly proportional to the stability of carbocation.
A
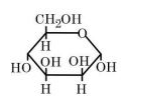
B
C
D
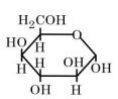
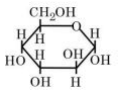
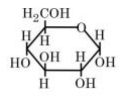
Solution
By Haworth structure of mannose
A
All these structures are in dynamic equilibrium with each other.
B
Each structure exists for equal amount of time.
C
$CO _3{ }^{2-}$ has a single structure i.e., resonance hybrid of the above three structures.
D
It is possible to identify each structure individually by some physical or chemical method.
Solution
Resonating structure are hypothetical and resonance hybrid is real structure which is weighted average of all the resonating structures
A
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
B
A is true but $R$ is false
C
$A$ is false but $R$ is true
D
Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$
Solution
No pollution occurs by combustion of hydrogen and very low density of hydrogen
A
A and B only
B
B and C only
C
A only
D
B only
Solution
Applying electrical neutrality principle in metal defficiency defect. $3 A ^{2+}$ are replaced by $2 A ^{3+}$, thus one vacant site per pair of $A ^{3+}$ is created
A
By using catalytic convertors in the automobiles/industry.
B
By complete combustion of fuel.
C
By using catalyst.
D
By using tall chimneys.
A
(A) - III, (B) - IV, (C) - II, (D) - I
B
(A) - III, (B) - II ,(C)- IV, (D) - I
C
(A) - I, (B) - IV, (C) - II, (D) - III
D
(A) - II ,(B)- IV,(C)- I, (D) - III
A
(A) - II, (B) - IV, (C) - I, (D) - III
B
(A) - IV, (B) - II, (C) - I, (D) - III
C
(A) - III, (B) - I, (C) - II, (D) - IV
D
(A) - II, (B) - I, (C) - III, (D) - IV
A
A and D only
B
A and C only
C
B and C only
D
B and D only
A
Both the Statements I and II are false
B
Both the Statements I and II are true
C
Statement I is false but Statement II is true
D
Statement I is true but Statement II is false
Solution
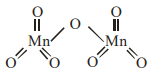
Chlorine oxides, $Cl _2 O , ClO _2, Cl _2 O _6$ and $Cl _2 O _7$ are highly reactive oxidising agents and tend to explode.
A
A is correct but $R$ is not correct
B
$A$ is not correct but $R$ is correct
C
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
D
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$
A
Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$
B
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
C
A is false but $R$ is true
D
$A$ is true but $R$ is false
Solution
Adsorption $\propto$ vanderwaal attraction forces $Z_c=\frac{3}{8}$ for all real gases
A
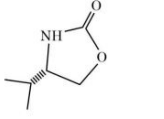
B
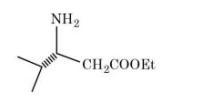
C
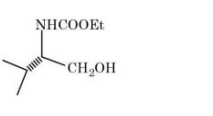
D
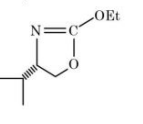
Solution
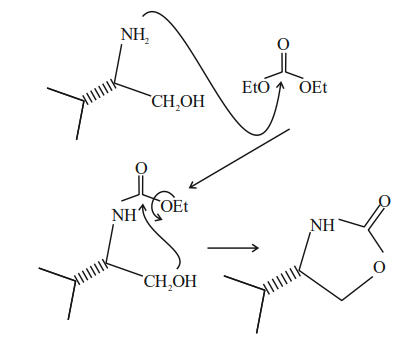
Initially lone pair electron of $- NH _2$ attack on electrophilic carbon, after then lone pair electron of oxygen attacks leading to formation of cyclic compound.
A
A, B and C only
B
B, C and D only
C
A and B only
D
A only
Solution
A. Beryllium oxide is amphoteric in nature.
B. Beryllium carbonate is kept in the atmosphere of $CO _2$ because it is thermally less stable.
C. Beryllium sulphate is readily soluble in water due to high degree of hydration.
D. Beryllium shows anomalous behaviour due to small size, high ionization energy and high value of $\phi$ (polarising power).
A
A, C & D only
B
A and B only
C
B, C & D only
D
B and C only
Solution
Incorrect statements are $C$ and $D$ only, correct choice is not available
Answer: 364
Solution
$ m =\frac{1000 \times M }{1000 \times d - M \times M . W \text { of solute }}$
$ =\frac{1000 \times 3}{1000 \times 1-(3 \times 58.5)}=3.64 $
$ =364 \times 10^{-2}$
Answer: 12
Solution
$HBrO _3$ (Bromic acid)
Ox. State of $Br =+5$
$HBrO _4$ (per bromic acid)
OX. State of $Br =+7$
Sum of Ox. State $=12$
Answer: 3
Solution

At equivalence point,
mmole of $KCl =$ mmole of $AgNO _3$
$=20 \,m$ mole
Volume of solution $=25 \,ml$
Mass of solution $=25\, gm$
Mass of solvent
$=25-$ mass of solute
$=25-\left[20 \times 10^{-3} \times 74.5\right]$
$=23.51 \,gm$
Molality of $KCl =\frac{\text { mole of } KCl }{\text { mass of solvent in } kg }$
$ =\frac{20 \times 10^{-3}}{23.51 \times 10^{-3}}=0.85 $
$ \text { i of } KCl =2(100 \% \text { ionisation }) $
$ \Delta T _{ f }= i \times K _{ f } \times m$
$ =2 \times 2 \times 0.85 $
$=3.4$
$ \approx 3$
Answer: 15
Solution
$[ A ]_{ t }=[ A ]_0 e ^{- kt }$
For $A$ : Let $[A]_t$ be $y$ and $[A]_0$ be $x ; k=\frac{\ln 2}{t_{1 / 2}}=$
$\frac{\ln 2}{15 \min }$
$y=x e^{-k t}$
$=x e^{-\left(\frac{\ln 2}{15}\right) t}$
For B: $[ B ]_{ t }=[ B ]_0 e ^{- kt }$
Let $[ B ]_{ t }= y ;[ B ]_0=4 x ; k =\frac{\ln 2}{ t _{1 / 2}}=\frac{\ln 2}{5 \min } $
$ y=4 x e^{-\left(\frac{\ln 2}{5}\right) t} $
$\Rightarrow x e^{-\left(\frac{\ln 2}{15}\right) t}=4 x e^{-\left(\frac{\ln 2}{5}\right) t} $
$ e ^{ t \left(\frac{\ln 2}{5} \frac{\ln 2}{15}\right)}=4$
$ t \times\left[\frac{\ln 2}{5}-\frac{\ln 2}{15}\right]=\ln 4 $
$ t \times \ln 2\left[\frac{1}{5}-\frac{1}{15}\right]=2 \ln 2 $
$ t =15 \min $
Answer: 12
Solution

$k_{ p _1}=\frac{\left(\frac{\alpha}{1+\alpha} \times p _1\right)^2}{\frac{1-\alpha}{1+\alpha} p _1} $
$ 3=\frac{\alpha^2 \times p _1}{1-\alpha^2}$

$ k _{ p _2}=\frac{\left(\frac{2 \alpha}{1+\alpha} \times p _2\right)^2}{\frac{1-\alpha}{1+\alpha} \times p _2} $
$ 1=\frac{4 \alpha^2 \times p _2}{1-\alpha^2} $
$ \frac{ k _{ p _1}}{ k _{ p _2}}=\frac{ p _1}{4 p _2} $
$\frac{3}{1}=\frac{ p _1}{4 p _2} $
$\therefore p _1: p _2=12: 1$
$ x =12$
Answer: 3
Solution
$MnO _4^{-}+8 H ^{+}+5 e ^{-} \rightleftharpoons Mn ^{2+}+4 H _2 O$
$ E = E ^{\circ}-\frac{0.059}{5} \log \frac{\left[ Mn ^{2+}\right]}{\left[ MnO _4^{-}\right]\left[ H ^{+}\right]^8} $
$ 1.282=1.54-\frac{0.059}{5} \log \frac{10^{-3}}{10^{-1} \times\left[ H ^{+}\right]^8} $
$ \frac{0.258 \times 5}{0.059}=\log \frac{10^{-2}}{\left[ H ^{+}\right]^8} $
$\Rightarrow 21.86=-2+8 pH $
$ \therefore pH =2.98 $
$ \simeq 3 $
Answer: 2
Solution
(A) $V _{ c }=1000 \,m / s ; h =6 \times 10^{-34} \,Js$;
$m _{ e }=9 \times 10^{-31} kg$
$\lambda=\frac{ h }{ mv }=\frac{6 \times 10^{-34}}{9 \times 10^{-31} \times 1000}=666.67 \times 10^{-9} \,m$
$=666.67 \,nm$
(B) The characteristic of electrons emitted is independent of the material of the electrodes of the cathode ray tube.
(C) The cathode rays start from cathode and move towards anode.
(D) The nature of the emitted electrons is independent on the nature of the gas present in cathode ray tube.
Answer: 2
Solution
As per the language of given question, the best possible isomeric structure is $Ph - CH = CH - O - CH _3$ (cis and trans). So, the answer is $2$.
JEE Main Mathematics Question Paper with Solution 2023 February 1st Shift 1 - Morning
A
$\min f^{\prime}(x)=1+\max g^{\prime}(x)$
B
there exist $0 < x_1 < x_2 < 3$ such that $f(x) < g(x), \forall x \in\left(x_1, x_2\right)$
C
$\max f(x)>\max g(x)$
D
there exists $\hat{x} \in[0,3]$ such that $f^{\prime}(\hat{x}) < g^{\prime}(\hat{x})$
Solution
$f ( x )=2 x +\tan ^{-1} x$ and $g ( x )=\ln \left(\sqrt{1+x^2}+x\right)$ and $x \in[0,3]$
$g ^{\prime}( x )=\frac{1}{\sqrt{1+x^2}}$
Now, $0 \leq x \leq 3$
$ 0 \leq x^2 \leq 9$
$ 1 \leq 1+x^2 \leq 10$
So $ 2+\frac{1}{10} \leq f^{\prime}(x) \leq 3 $
$ \frac{21}{10} \leq f^{\prime}(x) \leq 3 \text { and } \frac{1}{\sqrt{10}} \leq g^{\prime}(x) \leq 1$
option (4) is incorrect
From above, $g ^{\prime}( x )< f ^{\prime}( x ) \forall x \in[0,3]$
Option (1) is incorrect.
$f^{\prime}(x) \& g^{\prime}(x)$ both positive so $f(x) \& g(x)$ both are increasing
So $\max \left( f ( x )\right.$ at $x=3$ is $6+\tan ^{-1} 3$
$\operatorname{Max}(g(x)$ at $x=3$ is $\ln (3+\sqrt{10})$
And $6+\tan ^{-1} 3>\ln (3+\sqrt{10})$
Option (2) is correct
A
reflexive and symmetric but not transitive
B
reflexive and transitive but not symmetric
C
reflexive but neither symmetric nor transitive
D
an equivalence relation
Solution
Check for reflexivity:
As $3( a - a )+\sqrt{7}=\sqrt{7}$
which belongs to relation so relation is reflexive
Check for symmetric:
Take $a=\frac{\sqrt{7}}{3}, b=0$
Now (a, b) $\in R$ but $( b , a ) \notin R$
As $3(b-a)+\sqrt{7}=0$
which is rational so relation is not symmetric.
Check for Transitivity:
Take (a, b) as $\left(\frac{\sqrt{7}}{3}, 1\right)$
$\&(b, c)$ as $\left(1, \frac{2 \sqrt{7}}{3}\right)$
So now (a, b) $\in R \&( b , c ) \in R$ but $( a , c ) \notin R$ which means relation is not transitive
A
$7 \sqrt{3}$
B
$6 \sqrt{3}$
C
$4 \sqrt{3}$
D
$5 \sqrt{3}$
Solution
Shortest distance between two lines
$\frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{z-z_1}{a_3} \&$
$\frac{x-x_2}{b_1}=\frac{y-y_2}{b_2}=\frac{z-z_2}{b_3}$ is given as
$\frac{\begin{vmatrix}x_1-x_2 & y_1-y_2 & z_1-z_2 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{vmatrix}}{\sqrt{\left(a_1 b_3-a_3 b_2\right)^2+\left(a_1 b_3-a_3 b_1\right)^2+\left(a_1 b_2-a_2 b_1\right)^2}}$
$\frac{\begin{vmatrix}5-(3) & 2-(-5) & 4-1 \\ 1 & 2 & -3 \\ 1 & 4 & -5\end{vmatrix}}{\sqrt{(-10+12)^2+(-5+3)^2+(4-2)^2}}$
$\frac{\begin{vmatrix}8 & 7 & 3 \\ 1 & 2 & -3 \\ 1 & 4 & -5\end{vmatrix}}{\sqrt{(2)^2+(2)^2+(2)^2}}$
$ =\frac{|8(-10+12)-7(-5+3)+3(4-2)|}{\sqrt{4+4+4}} $
$ =\frac{16+14+6}{\sqrt{12}}=\frac{36}{\sqrt{12}}=\frac{36}{2 \sqrt{3}} $
$ =\frac{18}{\sqrt{3}}=6 \sqrt{3}$
A
$\frac{56}{111}$
B
$\frac{58}{111}$
C
$\frac{55}{111}$
D
$\frac{59}{111}$
Solution
$ T _{ r }=\frac{\left( r ^2+ r +1\right)-\left( r ^2- r +1\right)}{2\left( r ^4+ r ^2+1\right)} $
$\Rightarrow T _{ r }=\frac{1}{2}\left[\frac{1}{ r ^2- r +1}-\frac{1}{ r ^2+ r +1}\right] $
$ T_1=\frac{1}{2}\left[\frac{1}{1}-\frac{1}{3}\right] $
$T_2=\frac{1}{2}\left[\frac{1}{3}-\frac{1}{7}\right]$
$T_3=\frac{1}{2}\left[\frac{1}{7}-\frac{1}{13}\right]$
$ \vdots $
$ T _{10}=\frac{1}{2}\left[\frac{1}{91}-\frac{1}{111}\right] $
$\Rightarrow \displaystyle\sum_{ r =1}^{10} T _{ r }=\frac{1}{2}\left[1-\frac{1}{111}\right]=\frac{55}{111}$
A
2
B
4
C
0
D
6
Solution
Let $(\sqrt{3}+\sqrt{2})^{x^2-4}= t$
$ t +\frac{1}{ t }=10$
$\Rightarrow t =5+2 \sqrt{6}, 5-2 \sqrt{6} $
$\Rightarrow (\sqrt{3}+\sqrt{2})^{ x ^2-4}=5+2 \sqrt{6}, 5-2 \sqrt{6} $
$\Rightarrow x ^2-4=2,-2 \text { or } x ^2=6,2 $
$\Rightarrow x =\pm \sqrt{2}, \pm \sqrt{6}$
A
1216
B
1456
C
1072
D
1792
Solution
$ \frac{1+3+5+a+b}{5}=5$
$ a+b=16 \ldots \ldots(1) $
$ \sigma^2=\frac{\sum x_1^2}{5}-\left(\frac{\sum x}{5}\right)^2 $
$8=\frac{1^2+3^2+5^2+a^2+b^2}{5}-25 $
$ a^2+b^2=130 \ldots \ldots(2) $
$ \text { by }(1),(2) $
$ a=7, b=9 $
$ \text { or } a=9, b=7$
A
0
B
$\frac{-2 \pi}{3}$
C
$\pi-2 \sin ^{-1}\left(\frac{\sqrt{3}}{4}\right)$
D
$\pi-\sin ^{-1}\left(\frac{\sqrt{3}}{4}\right)$
Solution
$ \cos ^{-1}(2 x)-2 \cos ^{-1} \sqrt{1-x^2}=\pi $
$\cos ^{-1}(2 x)-\cos ^{-1}\left(2\left(1-x^2\right)-1\right)=\pi$
$ \cos ^{-1}(2 x)-\cos ^{-1}\left(1-2 x^2\right)=\pi $
$ -\cos ^{-1}\left(1-2 x^2\right)=\pi-\cos ^{-1}(2 x)$
Taking $\cos$ both sides we get
$\operatorname{Cos}\left(-\cos ^{-1}\left(1-2 x^2\right)\right)=\cos \left(\pi-\cos ^{-1}(2 x)\right)$
$ 1-2 x ^2=-2 x$
$2 x ^2-2 x -1=0$
On solving, $x =\frac{1-\sqrt{3}}{2}, \frac{1+\sqrt{3}}{2}$
As $x=[-1 / 2,1 / 2], x=\frac{1+\sqrt{3}}{2}=$ rejected
So $x=\frac{1-\sqrt{3}}{2} \Rightarrow x^2-1=-\sqrt{3} / 2$
$=2 \sin ^{-1}\left(x^2-1\right)=2 \sin ^{-1}\left(\frac{-\sqrt{3}}{2}\right)=\frac{-2 \pi}{3}$
A
$\frac{2^{51}}{50 !}$
B
$\frac{2^{50}}{50 !}$
C
$\frac{2^{51}}{51 !}$
D
$\frac{2^{50}}{51 !}$
Solution
$ \displaystyle\sum_{ r =1}^{26} \frac{1}{(2 r -1) !(51-(2 r -1)) !}=\displaystyle\sum_{ r =1}^{26}{ }^{51} C _{(2 r -1)} \frac{1}{51 !} $
$ =\frac{1}{51 !}\left\{{ }^{51} C _1+{ }^{51} C _3+\ldots .+{ }^{51} C _{51}\right\}=\frac{1}{51 !}\left(2^{50}\right)$
A
$\log _e 2$
B
$\log _e\left(\frac{2}{3}\right)$
C
0
D
$\log _e\left(\frac{3}{2}\right)$
Solution
$\displaystyle \lim _{n \rightarrow \infty}\left(\frac{1}{1+n}+\ldots+\frac{1}{n+n}\right)=\displaystyle\lim _{n \rightarrow \infty} \displaystyle\sum_{r=1}^n \frac{1}{n+r} $
$=\displaystyle\lim _{n \rightarrow \infty} \sum_{r=1}^n \frac{1}{n}\left(\frac{1}{1+\frac{r}{n}}\right) $
$=\int\limits_0^1 \frac{1}{1+x} d x=\left[\ell \ln (1+x]_0^1=\ell n 2\right.$
A
$x^2-19 x+90=0$
B
$x^2-20 x+99=0$
C
$x^2-18 x+80=0$
D
$x^2-22 x+120=0$
Solution

$ \left(\frac{\beta-3}{\alpha-2}\right)\left(\frac{1}{-2}\right)=-1 $
$ \beta-3=2 \alpha-4 $
$ \beta=2 \alpha-1 $
$ m_{ AH } \times m_{ BC }=-1$
$\Rightarrow \quad\left(\frac{\beta-2}{\alpha-1}\right)(-2)=-1$
$ \Rightarrow 2 \beta-4=\alpha-1 $
$ \Rightarrow 2(2 \alpha-1)=\alpha+3 $
$\Rightarrow 3 \alpha=5 $
$ \alpha=\frac{5}{3}, \beta=\frac{7}{3} $
$\Rightarrow H \left(\frac{5}{3}, \frac{7}{3}\right)$
$ \alpha+4 \beta=\frac{5}{3}+\frac{28}{3}=\frac{33}{3}=11 $
$ \beta+4 \alpha=\frac{7}{3}+\frac{20}{3}=\frac{27}{3}=9 $
$ x^2-20 x+99=0$
A
$2 \sqrt{14}$
B
$\frac{22 \sqrt{2}}{7}$
C
$3 \sqrt{14}$
D
$\frac{24 \sqrt{2}}{7}$
Solution

eq. of line PM $ \frac{x-2}{1}=\frac{y+1}{2}=\frac{z-3}{-1}=\lambda$
any point on line$=(\lambda+2,2 \lambda-1,-\lambda+3)$
for point ' $ m \text { ' }(\lambda+2)+2(2 \lambda-1)-(3-\lambda)=0$
$ \lambda=\frac{1}{2}$
$ \text { Point } m \left(\frac{1}{2}+2,2 \times \frac{1}{2}-1, \frac{-1}{2}+3\right)$
$ =\left(\frac{5}{2}, 0, \frac{5}{2}\right)$
For Image $Q (\alpha, \beta, \gamma)$
$\frac{\alpha+2}{2}=\frac{5}{2}, \frac{\beta-1}{2}=0 $
$ \frac{\gamma+3}{2}=\frac{5}{2} $
$ Q:(3,1,2) $
$ d =\left|\frac{3(3)+2(1)+2+29}{\sqrt{3^2+2^2+1^2}}\right| $
$ d =\frac{42}{\sqrt{14}}=3 \sqrt{14}$
A
12
B
4
C
2
D
6
Solution
$\begin{vmatrix}\lambda & 1 & 1 \\ 1 & \lambda & 1 \\ 1 & 1 & \lambda\end{vmatrix}=0$
$(\lambda+2)\begin{vmatrix}1 & 1 & 1 \\ 1 & \lambda & 1 \\ 1 & 1 & \lambda\end{vmatrix}=0$
$ (\lambda+2)\left[1\left(\lambda^2-1\right)-1(\lambda-1)+(1-\lambda)\right]=0 $
$(\lambda+2)\left[\left(\lambda^2-2 \lambda+1\right)=0\right.$
$ (\lambda+2)(\lambda-1)^2=0 \Rightarrow \lambda=-2, \lambda=1$
at $\lambda=1$ system has infinite solution, for inconsistent $\lambda=-2$
so $\sum\left(|-2|^2+|-2|\right)=6$
A
$\beta^2+2 \sqrt{\alpha}=\frac{19}{4}$
B
$\alpha^2+\beta^2=\frac{9}{2}$
C
$\alpha^2-\beta^2=4 \sqrt{3}$
D
$\beta^2-2 \sqrt{\alpha}=\frac{19}{4}$
Solution
$C_1 \rightarrow C _1+ C _2+ C _3 $
$f ( x ) =\begin{vmatrix}2+\sin 2 x & \cos ^2 x & \sin 2 x \\ 2+\sin 2 x & 1+\cos ^2 x & \sin 2 x \\ 2+\sin 2 x & \cos ^2 x & 1+\sin 2 x\end{vmatrix}$
$f(x)=(2+\sin 2 x)\begin{vmatrix}1 & \cos ^2 x & \sin 2 x \\ 1 & 1+\cos ^2 x & \sin 2 x \\ 1 & \cos ^2 x & 1+\sin 2 x\end{vmatrix}$
$ R_2 \rightarrow R_2-R_1$
$ R_3 \rightarrow R_3-R_1$
$f(x)=2+\sin 2 x)\begin{vmatrix}1 & \cos ^2 x & \sin 2 x \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}$
$=(2+\sin 2 x)(1)=2+\sin 2 x$
$=\sin 2 x \in\left[\frac{\sqrt{3}}{2}, 1\right]$
Hence $2+\sin 2 x \in\left[2+\frac{\sqrt{3}}{2}, 3\right]$
A
$3 x^2+5 x y+2 y^2=0$
B
$x^2-y^2-10 x y=0$
C
$3 x^2+x y-2 y^2=0$
D
$x^2-y^2+10 x y=0$
Solution
Equation of the pair of angle bisector for the homogenous equation $a x^2+2 h x y+b y^2=0$ is given as
$\frac{x^2-y^2}{a-b}=\frac{x y}{h}$
Here $a=2, h=1 / 2 \& b=-3$
Equation will become
$ \frac{x^2-y^2}{2-(-3)}=\frac{x y}{1 / 2} $
$ x ^2-y^2=10 x y $
$ x^2-y^2-10 x y=0$
A
area of $\triangle A B C$ is $\frac{27 \sqrt{3}}{2}$
B
$\sin 2 A+\sin 2 B+\sin 2 C=\sin A+\sin B+\sin C$
C
perimeter of $\triangle A B C$ is $18 \sqrt{3}$
D
$\overrightarrow{M A} \cdot \overrightarrow{M B}=-18$
Solution

If $\cos 2 A +\cos 2 B +\cos 2 C$ is minimum then $A =$ $B = C =60^{\circ}$
So $\triangle ABC$ is equilateral
Now in-radias $r=3$
So in $\triangle MBD$ we have
$ \operatorname{Tan} 30^{\circ}=\frac{M D}{B D}=\frac{r}{a / 2}=\frac{6}{a} $
$1 / \sqrt{3}=\frac{1}{a}=a=6 \sqrt{3}$
Perimeter of $\triangle ABC =18 \sqrt{3}$
Area of $\triangle ABC =\frac{\sqrt{3}}{4} a^2=27 \sqrt{3}$
A
$\frac{\pi}{12}-\frac{\sqrt{3}}{2} \log _e\left(\frac{2}{e \sqrt{3}}\right)$
B
$\frac{\pi}{12}+\frac{\sqrt{3}}{2} \log _e\left(\frac{2}{e \sqrt{3}}\right)$
C
$\frac{\pi}{12}+\frac{\sqrt{3}}{2} \log _e\left(\frac{2 \sqrt{3}}{e}\right)$
D
$\frac{\pi}{12}-\frac{\sqrt{3}}{2} \log _e\left(\frac{2 \sqrt{3}}{e}\right)$
Solution
Here I.F. $=\sec x$
Then solution of D.E :
$y(\sec x)=x \tan x-\ln (\sec x)+c$
Given $y(0)=1 \Rightarrow c=1$
$\therefore y (\sec x )= x \tan x -\ln (\sec x )+1$
At $x =\frac{\pi}{6}, y =\frac{\pi}{12}+\frac{\sqrt{3}}{2} \ln \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}$
A
12
B
11
C
10
D
9
Solution
$ \sqrt{(x-2)^2+y^2}=2 \sqrt{(x-3)^2+y^2} $
$ =x^2+y^2-4 x+4=4 x^2+4 y^2-24 x+36 $
$ =3 x^2+3 y^2-20 x+32=0 $
$ =x^2+y^2-\frac{20}{3} x+\frac{32}{3}=0 $
$ =(\alpha, \beta)=\left(\frac{10}{3}, 0\right) $
$\gamma=\sqrt{\frac{100}{9}-\frac{32}{3}}=\sqrt{\frac{4}{9}}=\frac{2}{3} $
$3(\alpha, \beta, \gamma)=3\left(\frac{10}{3}+\frac{2}{3}\right)$
$=12$
A
50
B
53
C
52
D
51
Solution
$ n p+n p q=5, n p \cdot n p q=6$
$ n p(1+q)=5, n^2 p^2 q=6$
$ n^2 p^2(1+q)^2=25, n^2 p^2 q=6 $
$ \frac{6}{q}(1+q)^2=25 $
$6 q^2+12 q+6=25 q$
$ 6 q^2-13 q+6=0 $
$ 6 q^2-9 q-4 q+6=0 $
$(3 q-2)(2 q-3)=0 $
$ q=\frac{2}{3}, \frac{3}{2}, q=\frac{2}{3} \text { is accepted }$
$ p=\frac{1}{3} \Rightarrow n \cdot \frac{1}{3}+n \cdot \frac{1}{3} \cdot \frac{2}{3}=5 $
$ \frac{3 n+2 n}{9}=5$
$ n=9$
So $6(n+p-q)=6\left(9+\frac{1}{3}-\frac{2}{3}\right)=52$
A
$\frac{4 \sqrt{3}}{3}$
B
$\frac{2 \sqrt{3}}{3}$
C
2
D
$\quad 2 \sqrt{3}$
Solution
$ \frac{d y}{d x}+\frac{x+a}{y-2}=0 $
$ \frac{d y}{d x}=\frac{x+a}{2-y} $
$ (2-y) d y=(x+a) d x $
$2 y \frac{-y}{2}=\frac{x^2}{2}+ ax + c$
$ a+c=-\frac{1}{2} \text { as } y(1)=0 $
$ X^2+y^2+2 a x-4 y-1-2 a=0 $
$ \pi r^2=4 \pi$
$ r^2=4 $
$ 4=\sqrt{a^2+4+1+2 a} $
$ (a+1)^2=0$
$ P, Q=(0,2 \pm \sqrt{3})$
Equation of normal at $P , Q$ are $y -2=\sqrt{3}( x -1)$
$ y -2=-\sqrt{3}(x-1) $
$ R =\left(1-\frac{2}{\sqrt{3}}, 0\right) $
$ S =\left(1+\frac{2}{\sqrt{3}}, 0\right) $
$RS =\frac{4}{\sqrt{3}}=4 \frac{\sqrt{3}}{3}$
A
$p \wedge(\sim q)$
B
$(\sim p) \wedge(\sim q)$
C
$(\sim p) \vee(\sim q)$
D
$(\sim p) \vee q$
Solution
$ \sim(q \vee((\sim q) \wedge p)) $
$ =\sim q \wedge \sim((\sim q) \wedge p) $
$ =\sim q \wedge(q \vee \sim p) $
$ =(\sim q \wedge q) \vee(\sim q \wedge \sim p) $
$ =(\sim q \wedge \sim p)$
Answer: 63
Solution
$ \int\left(x^{20}+x^{13}+x^6\right)\left(2 x^{21}+3 x^{14}+6 x^7\right)^{1 / 7} d x$
$ 2 x ^{21}+3 x ^{14}+6 x ^7= t $
$ 42\left( x ^{20}+ x ^{13}+ x ^6\right) dx = dt$
$\frac{1}{42} \int\limits_0^{11} t^{\frac{1}{7}} d t=\left(\frac{t^{\frac{8}{7}}}{\frac{8}{7}} \times \frac{1}{42}\right)_0^{11}$
$ =\frac{1}{48}\left(t^{\frac{8}{7}}\right)_0^{11}=\frac{1}{48}(11)^{8 / 7} $
$ l=48, m =8, n =7 $
$ l+ m + n =63$
Answer: 3501
Solution
$ {[\vec{u} \vec{v} \vec{w}]=\vec{u} \cdot(\vec{v} \times \vec{w})} $
$ \min .(|u||\vec{v} \times \vec{w}| \cos \theta)=-\alpha \sqrt{3401} $
$\Rightarrow \cos \theta=-1 $
$ |u|=\alpha \text { (Given) } $
$ |\vec{v} \times \vec{w}|=\sqrt{3401}$
$\vec{v} \times \vec{w}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ \alpha & 2 & -3 \\ 2 \alpha & 1 & -1\end{vmatrix}$
$ \vec{v} \times \vec{w}=\hat{i}-5 \alpha \hat{j}-3 \alpha \hat{k} $
$ |\vec{v} \times \vec{w}|=\sqrt{1+25 \alpha^2+9 \alpha^2}=\sqrt{3401} $
$34 \alpha^2=3400 $
$ \alpha^2=100$
$ \alpha=10 \,\,\, (\text { as } \alpha>0)$
So $ \vec{u}=\lambda(\hat{i}-5 \alpha \hat{j}-3 \alpha \hat{k})$
$ \vec{u}=\sqrt{\lambda^2+25 \alpha^2 \lambda^2+9 \alpha^2 \lambda}$
$\alpha^2=\lambda^2\left(1+25 \alpha^2+9 \alpha^2\right)$
$100=\lambda^2(1+34 \times 100) $
$ \lambda^2=\frac{100}{3401}=\frac{m}{n}$
Answer: 514
Solution
Divisible by $2 \rightarrow 450$
Divisible by $3 \rightarrow 300$
Divisible by $7 \rightarrow 128$
Divisible by $2$ & $7 \rightarrow 64$
Divisible by $3$ & $7 \rightarrow 43$
Divisible by $2$ & $3 \rightarrow 150$
Divisible by $2,3$ & $7 \rightarrow 21$
$\therefore$ Total numbers $=450+300-150-64-43+21=514$
Answer: 62
Solution
$ A =\int\limits_{-1}^0\left( x ^2-3 x \right) dx +\int \limits_0^2\left(3 x - x ^2\right) dx $
$ \Rightarrow A =\frac{ x ^3}{3}-\left.\frac{3 x ^2}{2}\right|_{-1} ^0+\frac{3 x ^2}{2}-\left.\frac{ x ^3}{3}\right|_0 ^2 $
$\Rightarrow A =\frac{11}{6}+\frac{10}{3}=\frac{31}{6} $
$ \therefore 12 A =62$
Answer: 50400
Solution
Vowels : $A,A,A,I,I,O$
Consonants : $S,S,S,S,N,N,T$
$\because$ Total number of ways in which vowels come together
$=\frac{\lfloor {8}}{\lfloor 4 \lfloor 2} \times \frac{\lfloor {6}}{\lfloor{3} \lfloor 2}=50400$
Answer: 11
Solution
$ A (2,6,2) \quad B (-4,0, \lambda), C (2,3,-1) D (4,5,0) $
$ \text { Area }=\frac{1}{2}|\overrightarrow{B D} \times \overrightarrow{A C}|=18$
$\overrightarrow{A C} \times \overrightarrow{B D}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 0 & -3 & -3 \\ 8 & 5 & -\lambda\end{vmatrix}$
$ =(3 \lambda+15) \hat{i}-\hat{j}(-24)+\hat{k}(-24) $
$ \overrightarrow{A C} \times \overrightarrow{B D}=(3 \lambda+15) \hat{i}+24 \hat{j}-24 \hat{k} $
$ =\sqrt{(3 \lambda+15)^2+(24)^2+(24)^2}=36 $
$ =\lambda^2+10 \lambda+9=0 $
$ =\lambda=-1,-9 $
$ |\lambda| \leq 5 \Rightarrow \lambda=-1 $
$ 5-6 \lambda=5-6(-1)=11$
Answer: 14
Solution
$ f(x)=x^2+g^{\prime}(1) x+g^{\prime \prime}(2)$
$ f^{\prime}(x)=2 x+g^{\prime}(1) $
$ f^{\prime \prime}(x)=2 $
$ g(x)=f(1) x^2+x\left[2 x+g^{\prime}(1)\right]+2 $
$ g^{\prime}(x)=2 f(1) x+4 x+g^{\prime}(1) $
$ g^{\prime \prime}(x)=2 f(1)+4 $
$ g^{\prime \prime}(x)=0 $
$ 2 f(1)+4=0 $
$ f(1)=-2 $
$ -2=1+g^{\prime}(1)=g^{\prime}(1)=-3$
So $ f^{\prime}(x)=2 x-3 $
$ f(x)=x^2-3 x+c $
$ c=0 $
$ f(x)=x^2-3 x $
$ g(x)=-3 x+2 $
$ f(4)-g(4)=14$
Answer: 1
Solution
$\frac{ dy }{ dx }+ y = k $
$ y \cdot e ^{ x }= k \cdot e ^{ x }+ c $
$ f (0)= e ^{-2} $
$ \Rightarrow c = e ^{-2}- k $
$ \therefore y = k +\left( e ^{-2}- k \right) e ^{- x } $
$ \text { now } k =\int\limits_0^2\left( k +\left( e ^{-2}- k \right) e ^{- x }\right) dx $
$ \Rightarrow k = e ^{-2}-1 $
$ \therefore y =\left( e ^{-2}-1\right)+ e ^{- x } $
$ f (2)=2 e ^{-2}-1, f (0)= e ^{-2} $
$ 2 f (0)- f (2)=1$
Answer: 754
Solution
$a_1+a_2+a_3+a_4=50 $
$ \Rightarrow 32+6 d=50 $
$ \Rightarrow d=3 $
$ \text { and, } a_{n-3}+a_{n-2}+a_{n-1}+a_n=170 $
$ \Rightarrow 32+(4 n-10) \cdot 3=170 $
$\Rightarrow n =14 $
$ a_7=26, a_8=29 $
$ \Rightarrow a_7 \cdot a_8=754$
Answer: 29














