JEE Main Physics Question Paper with Solution 2022 July 26th Shift 1 - Morning
A
3360 N
B
3380 N
C
3120 N
D
3240 N
Solution
Let acceleration of $100\, kg$ block $= a _1$
FBD of $100\, kg$ block w.r.t ground

$F - T - N _1=100 a _1$
FBD of $20$ block wrt $100 \,kg$

$ T -20 g =20(2)$
$ T =240 .....$(ii)
$N _1=20 a _1 \ldots \text {.... (iii) }$
FBD of $10\, kg$ block wrt $100\, kg$

$ a_1=26 \, m / s ^2 $
$F -240-20(26)=100 \times 26$
$ \Rightarrow F =3360 \,N$
A
4 m
B
20 m
C
30 m
D
50 m
Solution
Given: Frequency $f_1=6\, MHz$
Frequency $f_2=10\, MHz$
$ \lambda_1=\frac{ c }{ f _1}$
$ \lambda_2=\frac{ c }{ f _2}$
Wavelength bandwidth $=\lambda_2-\lambda_1=20 \, m$
A
$0.02 \,\min ^{-1}$
B
$2.7 \,\min ^{-1}$
C
$0.063 \,\min ^{-1}$
D
$6.3 \,\min ^{-1}$
Solution
At $t =0 $ disintegration rate $=4250\, dpm$
At $t =10$ disintegration rate $=2250 \,dpm$
$A=A_o e^{-\lambda t}$
$ 2250=4250 e ^{-\lambda(10)}$
$ \Rightarrow \lambda(10)=\ln \left(\frac{4250}{2250}\right) $
$ \Rightarrow \lambda=0.063 \,\min ^{-1}$
A
$3 \times 10^{16}$
B
$4.5 \times 10^{16}$
C
$4.5 \times 10^{17}$
D
$4.5 \times 10^{20}$
Solution
Wavelength of incident beam $\lambda=900 \times 10^{-9}$
Intensity of incident beam $= I =100 W / m ^2$
No. of photons crossing per unit sec
$ = n =\frac{ E _{\text {net }}}{ E _{\text {single photon }}}=\frac{ IA \lambda}{ hc } $
$ =\frac{(100)\left(1 \times 10^{-4}\right)\left(900 \times 10^{-9}\right)}{6.62 \times 10^{-34} \times 3 \times 10^8}=4.5 \times 10^{16}$
A
16
B
9
C
48
D
12
Solution
For a given light wavelength corresponding a medium of refractive index
$= $_________
and we know that fringe width ____
Therefore, $\beta_{\text {med }}=$ _____ $=\frac{12}{\underline{4}}=9 \,mm$
A
$6\, Vm ^{-1}$ along $x$-axis
B
$3\, Vm ^{-1}$ along z-axis
C
$6\, Vm ^{-1}$ along z-axis
D
$2 \times 10^{-8} Vm ^{-1}$ along z-axis
Solution
$c =\frac{ E _0}{ B _0} \Rightarrow E _0= cB _0 $
$ E _0=\left(3 \times 10^8\right)\left(2 \times 10^{-8}\right) $
$ E _0=6 \,Vm ^{-1}$
As, $\vec{ B }=$ along y-axis $\vec{ v }=$ along negative $x$-axis hence $ \vec{ E }_0=$ along z-axis
A
$\frac{1}{2}$
B
$\frac{1}{\sqrt{2}}$
C
$\frac{\sqrt{3}}{\sqrt{2}}$
D
$2: 1$
Solution
In case of L-R circuit
$Z =\sqrt{ X _{ L }^2+ R ^2} \&$ power factor
$P _1=\cos \phi=\frac{ R }{ Z }$
As $X _{ L }= R$
$\Rightarrow Z =\sqrt{2} R$
$\Rightarrow P _1=\frac{ R }{\sqrt{2} R } \Rightarrow P _1=\frac{1}{\sqrt{2}}$
In case of L-C-R circuit
$Z =\sqrt{ R ^2+\left( X _{ L }- X _{ C }\right)^2}$
As $X_{ L }=X_C$
$ \Rightarrow Z=R $
$ \Rightarrow P_2=\cos \phi=\frac{R}{R}=1$
$ \Rightarrow \frac{P_1}{P_2}=\frac{1}{\sqrt{2}}$
A
3
B
6
C
12
D
2
Solution
As $ \vec{F}=q(\vec{v} \times \vec{B}) $
$ \vec{a}=\frac{q}{m}(\vec{v} \times \vec{B})$
So, $\vec{a} \& \vec{B}$ are $\perp$ to each other
Hence, $\vec{a} \cdot \vec{B}=0$
$ (\alpha \hat{i}-4 \hat{j}) \cdot(2 \hat{i}+3 \hat{j})=0$
$ \alpha(2)+(-4)(3)=0 $
$\alpha=\frac{12}{2} \Rightarrow \alpha=6$
A
$1: 1$
B
$1: 2$
C
$2: 1$
D
$4: 1$
Solution
At centre $B = N \left(\frac{\mu_0 i }{2 R }\right)$
$ B _{ x }=200\left(\frac{\mu_0 i }{2 \times 20 cm }\right) $
$B _{ y }=400\left(\frac{\mu_0 i }{2 \times 20 cm }\right)$
$\frac{ B _{ x }}{ B _{ y }}=\frac{1}{2}$
A
10A
B
20 A
C
4A
D
40A
Solution

Given circuit is balanced wheat stone bridge Hence $2 \Omega$ can be neglected
$ R _{ net }=4 \Omega$
$ I =\frac{40}{4}$
$ I=10 A$
A
$200 \,\mu C$
B
$200 \, C$
C
$10 \, \mu C$
D
$10 \, C$
Solution

Total charge $= q _1+ q _2+ q _2+ q _4$
$=1 \times 20+2 \times 20+4 \times 20+3 \times 20=200 \,\mu C$
A
Circular
B
Ellipitical
C
Sinusoidal
D
Straight line
Solution
For a particle in SHM, its speed depends on position as
$v =\omega \sqrt{ A ^2- x ^2}$
Where $\omega$ is angular frequency and $A$ is amplitude
Now $v^2=\omega^2 A^2-\omega^2 x^2$
So, $\frac{v^2}{(\omega A )^2}+\frac{x^2}{( A )^2}=1$
So graph between $v$ and $x$ is elliptical
A
$5810 \,J$
B
$3486\, J$
C
$11620\, J$
D
$6972 \,J$
Solution
For a quasi-static process the change in internal energy of an ideal gas is
$\Delta U = nC _{ V } \Delta T $
$ = n \times \frac{3 R }{2} \times \Delta T$
[molar heat capacity at constant volume for mono atomic gas $=\frac{3 R }{2}$ ]
$\Delta U =7 \times \frac{3}{2} \times 8.3 \times 40=3486 \,J$
A
$P$
B
$8 P$
C
$32 P$
D
$64 P$
Solution
Constant entropy means process is adiabatic
$ PV ^\gamma=$ constant
$ V _2=\frac{ V _1}{8} $
$ P _1 V _1^\gamma= P _2 V _2^\gamma $
$P _1 V _1^\gamma= P _2\left(\frac{ V _1}{8}\right)^{5 / 3} $
$ P _1 V _1^{5 / 3}=\frac{ P _2 V _1^{5 / 3}}{32} $
$ P _2=32 P _1$
A
$8.5 \times 10^{-4} J$
B
$8.2 \times 10^{-4} J$
C
$7.5 \times 10^{-4} J$
D
$5.3 \times 10^{-4} J$
Solution
Initial surface energy $= TA$
Where $T$ is surface tension and $A$ is surface area
$ U _{ i }=\left(\frac{75 \times 10^{-5}}{10^{-2}} \frac{ N }{ m }\right) \times\left[4 \pi\left(1 \times 10^{-2}\right)^2\right] $
$=75 \times 10^{-3} \times 4 \pi \times 10^{-4}=942 \times 10^{-7} J$
To get final radius of drops by volume conservation
$\frac{4}{3} \pi R ^3=729\left(\frac{4}{3} \pi r ^3\right)$
$ R =$ Initial radius
$ r =$ final radius
$ r =\frac{ R }{(729)^{1 / 3}}=\frac{ R }{9}=\frac{1}{9} cm$
Final surface energy
$U _{ f }=729[ TA ]$
$=729\left[\frac{75 \times 10^{-5}}{10^{-2}} \frac{ N }{ m }\right] \times\left[4 \pi\left(\frac{1}{9} \times 10^{-2}\right)^2\right] $
$=729\left[75 \times 10^{-3} \times \frac{4 \pi \times 10^{-4}}{81}\right] $
$ =9\left[942 \times 10^{-7} J \right]$
Gain in surface energy $ \Delta U =9 \times 942 \times 10^{-7}-942 \times 10^{-7} $
$ =8 \times 942 \times 10^{-7} J =7536 \times 10^{-7} J$
$ =7.5 \times 10^{-4} J $
A
$1 \%$
B
$3 \%$
C
$4 \%$
D
$0.5 \%$
Solution
Acceleration due to gravity at a height $h << R$ is
$ g ^{\prime}= g \left(1-\frac{2 h }{ R }\right) $
$ \therefore \frac{\Delta g }{ g }=\frac{2 h }{ R } $
$ \Rightarrow \frac{\Delta g }{ g } \times 100=\frac{2 h }{ R } \times 100 $
$=2 \times \frac{32}{6400} \times 100=1 \%$
A
$\frac{ V }{2 \sqrt{2}}$
B
$\frac{v}{2}$
C
$\frac{v}{4}$
D
$\frac{ v }{\sqrt{2}}$
Solution

using energy conservation
$\frac{1}{2} mv ^2 \times 2=\frac{1}{2} kx ^2$
$\Rightarrow \frac{1}{4} v ^2=\frac{1}{2} \times 2 \times x ^2$
$\therefore x =\frac{ v }{2}$
A
$T =700 \,N$ while climbing upward
B
$T =350\, N$ while going downward
C
Rope will break while climbing upward
D
Rope will break while going downward
Solution
F.B.D of monkey while moving downward

Using Newton's second law
$mg - T = ma _1 $
$\therefore 500- T =50 \times 4 \Rightarrow T =300\, N$
F.B.D of monkey while moving up

Using Newton's second law of motion
$T - mg = ma _2 $
$\Rightarrow T -500=50 \times 5$
$\Rightarrow T =750 \,N$
Breaking strength of string $=350 \, N$
$\therefore $ String will break while monkey is moving upward
A
$1: \sqrt{2}$
B
$2: 1$
C
$\sqrt{2}: 1$
D
$1: 2$
Solution
Time taken to reach maximum height
$ t =\frac{ u \sin \theta}{ g } $
$ \therefore \frac{ u _1 \sin \theta_1}{ g }=\frac{ u _2 \sin \theta_2}{ g }$
$ \Rightarrow u _1 \sin 30= u _2 \sin 45$
$ \Rightarrow \frac{ u _1}{ u _2}=\frac{1 / \sqrt{2}}{1 / 2}=\frac{\sqrt{2}}{1}$
A
$6.8 \,cm ^2$
B
$3.4 \,cm ^2$
C
$3.9\, cm ^2$
D
$2.4\, cm ^2$
Solution
L.C. $=\frac{ P }{ N }=\frac{0.5 mm }{50}=0.01\, mm$
Length of wire $=6.8 \, cm$
Diameter of wire $=1.5 \, mm +7 \times$ L.C
$=1.5\, mm +7 \times .01=1.57 \, mm$
Curved surface area $=\pi D \ell$
$=3.14 \times 6.8 \times 1.57 \times 10^{-1} cm ^2$
$=3.352 \, cm ^2=3.4\, cm ^2$
Answer: 5
Solution
$u_x=1 $
$ y=5 x(1-x) $
$ \frac{d y}{d t}=5 \frac{d x}{d t}-10 x \frac{d x}{d t}$
For initial y-component of velocity
$u _{ y }=\left(\frac{ dy }{ dt }\right)_{ x =0} \Rightarrow 5(1)=5 $
$ \vec{ u }_{ y }=5 \hat{ j }$
Answer: 5
Solution

using conservation of mechanical energy
$mg 2 R =\frac{1}{2} I _{\text {disc }} \omega^2+\frac{1}{2} I _{\text {particle }} \omega^2$
$mg 2 R =\frac{\omega^2}{2}\left[\frac{ mR ^2}{2}+ mR ^2\right] $
$ mg 2 R =\frac{\omega^2}{2} \frac{3}{2} mR ^2$
$ \frac{3}{4} \omega^2=\frac{2 g }{ R } $
$ \omega^2=\frac{8 g }{3 R } $
$ \omega=\sqrt{\frac{80}{3 R}}$
Given $\omega=4 \sqrt{\frac{x}{3 R}} $
$16 \frac{x}{3 R}=\frac{80}{3 R}$
$x=5$
Answer: 2
Solution
$ L =1 m $
$ \Delta L =0.4 \times 10^{-3} m $
$ m =1 \,kg $
$ d =0.4 \times 10^{-3} m $
$ \frac{ F }{ A }= Y \frac{\Delta L }{ L }$
$ Y =\frac{ FL }{ A \Delta L }=\frac{( mg ) \cdot(1)}{\left(\frac{\pi d ^2}{4}\right) 0.4 \times 10^{-3}} $
$\Rightarrow \frac{10 \times 4}{\pi\left(0.4 \times 10^{-3}\right)^2 \times 0.4 \times 10^{-3}}$
$ Y =\frac{40}{\pi\left(0.4 \times 10^{-3}\right)^3} $
$ Y =\frac{40 \times 7}{22 \times 64 \times 10^{-3} \times 10^{-9}} $
$ Y =0.199 \times 10^{-12} N / m ^2$
$ \frac{\Delta Y }{ Y }=\frac{\Delta F }{ F }+\frac{\Delta L }{ L }+\frac{\Delta A }{ A }+\frac{\Delta(\Delta L )}{(\Delta L )} $
$ =\frac{0.02}{0.4}+2 \frac{\Delta d }{ d }=\frac{0.2}{4}+2 \times \frac{0.01}{0.4}$
$ =\frac{0.1}{2}+\frac{0.1}{2}=0.1$
$ \Rightarrow \Delta Y =0.1 \times Y $
$=0.199 \times 10^{11}=1.99 \times 10^{10}$
Answer: 200
Solution
$ f _1=100= f _0\left(\frac{ C }{ C - V _{ s }}\right) $
$ C =$ speed of sound
$ V _{ s }=$ speed of source
$ f _2=50= f _0\left(\frac{ C }{ C + V _{ s }}\right)$
$ \frac{ f _1}{ f _2}=2=\frac{ C + V _{ s }}{ C - V _{ s }} $
$ 2 C -2 V _{ s }= C + V _{ s } $
$3 V _{ s }= C $
$ V _{ S }=\frac{ C }{3}$
$ 100= f _0 \frac{ C }{\frac{2 C }{3}}=\frac{3}{2} f _0$
$ f _0=\frac{200}{3}$
Answer: 60
Solution

Capacitance of each capacitor
$ C _1=\frac{ A 3 \in_0}{\frac{1}{2}}=6 A \in_0 $
$C _2= A 4 \in_0=4 A \in_0$
Equivalent capacitance
$C _{ eq }=\frac{ C _1 C _2}{ C _1+ C _2} \Rightarrow \frac{24}{10} A \in_0 $
$ q _{ net }= C _{ eq }(\Delta V ) \Rightarrow 240 A \in_0$
$\Delta V _2=\frac{240 A \epsilon_0}{4 A \epsilon_0}=60\, V$
$ (\Delta V _2=$ Potential drop across $C _2)$
$V _{\text {foil }}=60\, V$
Answer: 20
Solution
Initially, $\frac{ P }{ Q }=\frac{40\, cm }{60\, cm }=\frac{2}{3} ....$(1)
Finally, $\frac{ P + x }{ Q }=\frac{80 \,cm }{20 \,cm }=\frac{4}{1}.....$(2)
Divide (2) by (1)
$ \frac{P+x}{P}=4 \times \frac{3}{2}=6$
$\Rightarrow 1+\frac{x}{P}=6 \Rightarrow \frac{x}{P}=5$
$ \therefore x=5 P=5 \times 4=20 \Omega$
Answer: 44
Solution
At very high frequencies,
$X _{ C }=\frac{1}{\omega C } \approx 0$
Also $X _{ L }=\omega L \approx \infty$
Thus, equivalent circuit can be redrawn as

$ Z =1+2+2=5 \,\Omega $
$I =\frac{220 V }{5 \Omega}=44\, A$
Answer: 10
Solution

For point $ B, \frac{1}{ u }=-0.10\, cm ^{-1}, \frac{1}{ v }=0$
$ \therefore$Thus, $u =-10 \,cm , v =\infty $
i.e. $ f =10 \,cm $
$ \Rightarrow \frac{1}{10 cm }=(1.5-1)\left(\frac{2}{ R }\right)=\frac{1}{ R }$
$ \Rightarrow R =10\, cm$
Answer: 5
Solution
For first line of Lyman
$ \frac{1}{\lambda}= R \left(1-\frac{1}{4}\right)= R \left(\frac{3}{4}\right) $
$ \Rightarrow \lambda=\frac{4}{3 R} $
$ 3^{\text {rd }} \text { line(Paschen) } $
$ \frac{1}{\lambda_3}= R \left(\frac{1}{3^2}-\frac{1}{6^2}\right)=\frac{ R }{9} \times \frac{3}{4} $
2nd line(Balmer) $ \frac{1}{\lambda_2}= R \left(\frac{1}{2^2}-\frac{1}{4^2}\right)=\frac{ R }{4} \times \frac{3}{4} $
Thus $ a \lambda=\lambda_3-\lambda_2=\frac{12}{ R }-\frac{16}{3 R }=\frac{20}{3 R }$
putting (1) $ a\left(\frac{4}{3 R}\right)=\frac{20}{3 R} \Rightarrow a=5 $
Answer: 9
Solution
Consider input $120\,V$

$I=\frac{(120-60) V }{4000 \Omega}=0.015\, A$
Thus $ I _2= I - I _{ L }$
$=0.015-0.006=0.009\, A =9 \,mA$
JEE Main Chemistry Question Paper with Solution 2022 July 26th Shift 1 - Morning
A
(A) - (I), (B) - (II), (C) - (III), (D) - (IV)
B
(A) - (IV), (B) - (III), (C) - (II), (D) - (I)
C
(A) - (II), (B) - (IV), (C) - (I), (D) - (III)
D
(A) - (III), (B) - (IV), (C) - (II), (D) - (I)
Solution
A
(A) - (III), (B) - (I), (C) - (II), (D) - (IV)
B
(A) - (III), (B) - (II), (C) - (I), (D) - (IV)
C
(A) - (IV), (B) - (III), (C) - (I), (D) - (II)
D
(A) - (IV), (B) - (II), (C) - (III), (D) - (I)
Solution
Sol. $ 2 SO _2( g )+ O _2( g ) \xrightarrow{ V _2 O _5} 2 SO _3( g )$ :
contact process
$4 NH _3( g )+5 O _2( g ) \xrightarrow { Pt ( s )- Rh ( s )} 4 NO ( g )+6 H _2 O ( g ) \text { : }$
Ostwald's process
$N _2( g )+3 H _2( g ) \xrightarrow{ Fe ( s )} 2 NH _3( g ) ; $ Haber's process
Vegetable oil $(l)+ H _2( g ) \xrightarrow{ Ni ( s )}$ vegetable ghee
Hydrogenation
A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are incorrect.
C
Statement I is correct but Statement II is incorrect.
D
Statement I is incorrect but Statement II is correct.
Solution
In $Cl _2$ molecule, the covalent radius is half of the internuclear distance, so statement(I) is false.
For the same element, anion has lower effective nuclear charge than atom $\Rightarrow$ so anion is larger than atom. $\Rightarrow$ statement (II) is correct.
A
Low melting point
B
High boiling point
C
High electrical conductivity
D
Less tendency to be soluble in melts than impurities
Solution
Liquation is used to purify metals having lower melting point than impurities present in them.
A
Urea
B
Formaldehyde
C
Formic acid
D
Ethanol
Solution
Urea acts as stabiliser for $H_2O_2$.
A
(A), (D) and (E)
B
(A) , (B) and (D)
C
(D) and (E)
D
(B) , (C) and (D)
Solution
$2 BeCl _2+ LiAlH _4 \rightarrow 2 BeH _2+ LiCl + AlCl _3$
A
$B ( OH )_3$ and $NH _3$
B
$B _2 H _6$ and $NH _3$
C
$B _2 H _6$ and $HN _3$
D
$NH _3$ and $B _2 O _3$
Solution
$3 B _2 H _6+6 NH _3 \xrightarrow{\Delta} 2 B _3 N _3 H _6+12 H _2$
A
$2 H _2 O _2 \rightarrow 2 H _2 O + O _2$
B
$2 NO _2+ H _2 O \rightarrow HNO _3+ HNO _2$
C
$MnO _4^{-}+4 H ^{+}+3 e ^{-} \rightarrow MnO _2+2 H _2 O$
D
$3 MnO _4^{2-}+4 H ^{+} \rightarrow 2 MnO _4^{-}+ MnO _2+2 H _2 O$

A
5
B
1
C
7
D
2
Solution
In acidic medium,
$\overset{+7}{MnO _4^{-}} \rightarrow Mn ^{+2}$
change in ox. no. $=5$
A
$C _2 H _6$ and $Cl _2$
B
$\dot{ C } HCl _2$ and $H _2$
C
$\dot{ C } H _3$ and $HCl$
D
$C _2 H _6$ and $HCl$
Solution
$\dot{ Cl } + CH _4 \longrightarrow \dot{ C } H _3+ HCl$
A
Steam distillation
B
2-5 ft long column of silica gel
C
Sublimation
D
Preparative TLC (Thin Layer Chromatography)
Solution

Solvent polarity has been related to $R_f$ value of nitrocompounds.
$100\, mg$ p-nitrophenol and picric acid have different $R_f$ value on silica gel plate
$\therefore$ Preparative TLC is best to separate $100 \,mg$ of para nitrophenol and picric acid
A
Hyperconjugation in substrate
B
Polarity of solvent
C
Free radical formation
D
Electromeric effect of the substrate
Solution

Difference in reactions is observed due to solvent polarity, which
(i) Ionizes phenol to make more reactive phenoxide ion
(ii) Increases electrophilicity of bromine.
A
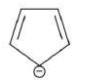
B
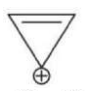
C
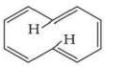
D
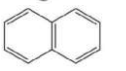
Solution
$[10]$ Annulene, although follow $(4 n+2) \pi$ electron rule, but it is non-aromatic due to its non planar nature. It is nonplanar due to repulsion of $C - H$ bonds present inside the ring.
A
$CH_3 - C \equiv N$
B
$Ph - C \equiv N$
C
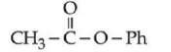
D
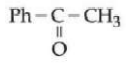
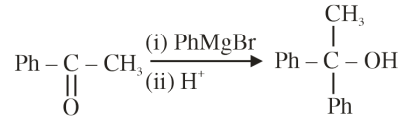
A
(A) > (B) > (C) > (D)
B
(A) > (C) > (D) > (B)
C
(C) > (A) > (D) > (B)
D
(C) > (D) > (B) > (A)
Solution

Since diazonium ion is a cation hence it is stabilized by electron donating groups and destabilized by electron withdrawing group. Hence Stability order should be $A > C > D > B$.
A
Cationic detergent
B
Soap
C
Anionic detergent
D
Non-ionic detergent
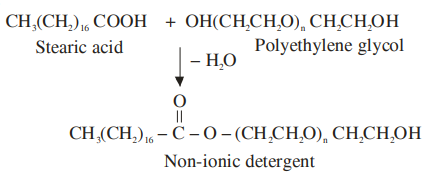
A
Both (A) and (R) are true and (R) is the correct explanation of (A).
B
Both (A) and (R) are true but (R) is not the correct explanation of (A).
C
(A) is true, but (R) is false.
D
(A) is false, but (R) is true.
Solution

Friedel Craft Alkylation does not occur on
this deactivated ring.
Answer: 24
Solution
$ ppm =\frac{ W _{ Mg }}{ V _{\text {soln }}} \times 10^6=48 $
$ \Rightarrow W _{ Mg }=\frac{48 \times 2 \times 1000}{10^6} $
$ =48 \times 2 \times 10^{-3} g$
$ n _{ Mg }=\frac{ W _{ Mg }}{24}=\frac{48 \times 2 \times 10^{-3}}{24} $
$ =4 \times 10^{-3}$
Number of $ Mg$ atoms $=4 \times 10^{-3} \times 6.02 \times 10^{23}$
$=4 \times 6.02 \times 10^{20} $
$=24.08 \times 10^{20} $
$ \therefore x =24.08$
Answer: 2
Solution
Let $ W _{ H _2}=40 g \Rightarrow n _{ H _2}=\frac{40}{2}=20$
$W _{ O _2}=60 g \Rightarrow n _{ O _2}=\frac{60}{32}=\frac{15}{8}$
$ P _{ H _2}=\left(\frac{20}{20+\frac{15}{8}}\right) \times 2.2$
$ =\frac{20}{20+1.875} \times 2.2$
$ =\frac{20}{21.875} \times 2.2$
$=2.0114 $
$ \simeq 2.01 \,bar$
Answer: 1758
Solution
$ v_{ e }= x v_{ N } $
$ \lambda_{ e }=\lambda_{ N } $
$ \Rightarrow \frac{ h }{ m _{ e } v_{ e }}=\frac{ h }{ m _{ N } v_{ N }} $
$ v_{ e }=\frac{ m _{ N }}{ m _{ e }} \cdot v _{ N }$
$ =\frac{1.6 \times 10^{-27}}{9.1 \times 10^{-31}} v_{ N }$
$ v_{ e }=1758.24 \times v_{ N } $
$ \therefore x =1758.24$
Answer: 200
Solution
$C ( s )+ O _2( g ) \rightarrow CO _2( g ) ; \Delta H =- x\, kJ / mole$
$ Q = C \Delta T =20 \,kJ \times 2$
$40\, kJ$ heat is released for $2.4 g$ of $C$
For $1$ mole '$C$' :
$Q=\frac{40}{2.4} \times 12$
$=\frac{400}{24} \times 12=200\,kJ / mole$
$Q =\Delta E =\Delta H =200\, kJ \left(\because \Delta n _{ g }=0\right)$
$ x =200$
Answer: 54
Solution
$ n _{ HNO _3}=0.5 \times 0.8$
$ =0.4 $ mole
$\left( n _{ HNO _3}\right)_{\text {remains }}=0.4-\frac{11.5}{63}$
$ =0.4-0.1825 $
$ =0.2175 $
Molarity $=\frac{0.2175}{400} \times 1000$
$ =\frac{0.2175}{0.4} $
$ =0.5437 mole / lit . $
$\simeq 0.54 mole / lit . $
$ =54 \times 10^{-2} mol / lit .$
Answer: 2
Solution
$ K _{ eq }^{\prime}=\frac{1}{\sqrt{ K _{ eq }}}=\frac{1}{\sqrt{2 \times 10^{15}}}= x \times 10^{-8} $
$\Rightarrow \frac{1}{\sqrt{20}} \times \frac{1}{10^7}= x \times 10^{-8} $
$\Rightarrow \frac{1}{\sqrt{20}} \times 10^{-7}= x \times 10^{-8} $
$\frac{10}{\sqrt{20}}= x $
$ \Rightarrow x =\frac{\sqrt{10}}{\sqrt{2}}=\sqrt{5}=2.236 $
$ \simeq 2.24$
Answer: 3
Solution
$Fe _3 O _4 \xrightarrow{+8 e ^{-}} 3 Fe$
Charge for 1 mole $Fe =8 / 3 F$
$=2.67 F$
Answer: 2
Solution
$ t _{\frac{1}{2}} \propto \frac{1}{\left[ A _0\right]^{ n -1}} $
$ {[100] \propto \frac{1}{(0.5)^{ n -1}}}$
$ (50) \propto \frac{1}{(1)^{n-1}} $
${[2]^1=\left[\frac{1}{0.5}\right]^{n-1}}$
$ {[2]^1=[2]^{n-1}} $
$ n-1=1 $
$ n=2$ order $=2$
Answer: 0
Solution

number of unpaired $e ^{-}=3$
$\mu=\sqrt{15} BM$
Difference in spin only magnetic moment
$=0$
JEE Main Mathematics Question Paper with Solution 2022 July 26th Shift 1 - Morning
A
4
B
10
C
11
D
16
Solution
$ f(x)-f(x / 3)=x / 3$
$ f(x / 3)-f\left(x / 3^2\right)=x / 3^2$
.... on adding
$f(x)-\displaystyle\lim _{n \rightarrow \infty} f\left(\frac{x}{3^n}\right)=x\left(\frac{1}{3}+\frac{1}{3^2} \ldots \infty\right) $
$ f(x)-f(0)=\frac{x}{2}$
$ f(8)=7 ; f(0)=3 $
$ f(x)=x / 2+3 $
$ f(14)=10$
A
$\arg z _2=\pi-\tan ^{-1} 3$
B
$\arg \left( z _1-2 z _2\right)=-\tan ^{-1} \frac{4}{3}$
C
$\left|z_2\right|=\sqrt{10}$
D
$\left|2 z_1-z_2\right|=5$
Solution
$AB = AO \cdot z ^{-i \pi / 2}=-2+i$
So $OB =(-2+i)+(1+2 i)$
$ z _2=-1+3 i $
$ \therefore\left|2 z _1- z _2\right|=\sqrt{10}$
A
$3 \sqrt{5}$
B
4
C
$\frac{26}{9}$
D
$\frac{10}{3}$
Solution
$D = \begin{vmatrix} 8 & 1 & 4 \\1 & 1 & 1 \\\lambda & -3 & 0\end{vmatrix}=0 \Rightarrow \lambda=4$
Also $D _1= D _2= D _3=0$
So $\mu=-2$
Point $\left(4,-2,-\frac{1}{2}\right)$
Distance from plane $=\frac{10}{3}$
A
$-1$
B
2
C
1
D
$-\sqrt{2}$
Solution
Let $A=\begin{bmatrix} a & b \\ c & d \end{bmatrix} ; ad - bc =-1$
$ | A + I ||\operatorname{adj} A + I |=4$
$ \Rightarrow ad - bc + a + d +1=2 \text { or }-2$
$ a + d =2 \text { or }-2$
A
3
B
5
C
7
D
9
Solution
$ A =\int\limits_1^3 y ^{ a } \cdot dy =\left.\frac{ y ^{ a +1}}{ a +1}\right|_1 ^3=\frac{364}{3} $
$ \Rightarrow a =5$
A
560
B
1540
C
1330
D
2600
Solution
$ \left(\left(2^1 2^2 \ldots .2^{60}\right)\left(4^1 \cdot 4^2 \ldots \ldots 4^{ n }\right)\right)^{\frac{1}{60+ n }}=2^{\frac{225}{8}} $
$ \left(2^{30 \times 61} 4^{\frac{ n ( n +1)}{2}}\right) \frac{1}{60+ n }=2^{\frac{225}{8}} $
$ 2^{1830+ n ^2+ n }=2^{\frac{(225)(60+ n )}{8}} $
$ =8 n ^2-217 n +1140=0 $
$ n =20, \frac{57}{8} $
$\displaystyle \sum_{ k =1}^{ n } nk - k ^2=\frac{ n ^2( n +1)}{2}-\frac{ n ( n +1)(2 n +1)}{6} $
$=1330$
A
1
B
-1
C
e
D
0
Solution
$ \displaystyle\lim _{x \rightarrow 0} \frac{\left(\ln \left(1+x^2+x^4\right)\right) \cos x}{1-\cos ^2 x} $
$ \displaystyle\lim _{x \rightarrow 0} \frac{\left(\frac{\ln \left(1+x^2+x^4\right)}{x^2+x^4}\right) x^2\left(1+x^2\right) \cos x}{\left(\frac{\sin ^2 x}{x^2}\right) x^2}=1 $
$ \therefore k=1$
A
-10
B
10
C
8
D
-8
Solution
$f(x)= \begin{cases}x+a ; x \leq 0 \\|x-4| ; x>0\end{cases} ; g(x)= \begin{cases} x+1 ; x<0 \\(x-4)^2+b ; x \geq 0\end{cases}$
For continuity $a=4$ and $b=-15$
$g ( f (2))+ f ( g (-2)) $
$ = g (2)+ f (-1)=-8$
A
$(-6,-2)$
B
$(2,6)$
C
$[-6,-2) \cup(2,6]$
D
$[-\sqrt{6},-2) \cup(2, \sqrt{6}]$
Solution
$ f (1)=3 $
For $ x < 1, f ^{\prime}( x )=3 x ^2-2 x +10>0$
$ \Rightarrow f ( x ) $ is increasing
For $ x >1, f ^{\prime}( x ) < 0 $
$ \Rightarrow $ function is decreasing.
$\displaystyle\lim _{ x \rightarrow 1^{+}} f ( x )=-2+\log _2\left( b ^2-4\right) $
For maximum value at $ x =1$
$ 3 \geq-2+\log _2\left( b ^2-4\right) $
$ 32 \geq b ^2-4>0$
$ b \in[-6,-2) \cup(2,6]$
A
$2 \sqrt{2} f \left(\frac{ a }{2}\right)= f ^{\prime}\left(\frac{ a }{2}\right)$
B
$f\left(\frac{a}{2}\right) f^{\prime}\left(\frac{a}{2}\right)=\sqrt{2}$
C
$\sqrt{2} f \left(\frac{ a }{2}\right)= f ^{\prime}\left(\frac{ a }{2}\right)$
D
$f \left(\frac{ a }{2}\right)=\sqrt{2} f ^{\prime}\left(\frac{ a }{2}\right)$
Solution
$ a =\frac{1}{ n } \displaystyle\sum_{ k =1}^{ n } \frac{2}{1+\left(\frac{ k }{ n }\right)^2}=\int_0^1 \frac{2}{1+ x ^2} dx =\frac{\pi}{2} $
$ f ( x )=\tan \left(\frac{ x }{2}\right) ; x \in(0,1) $
$ f \left(\frac{\pi}{4}\right)=\sqrt{2}-1 $
$ f ^{\prime}\left(\frac{\pi}{4}\right)=\frac{1}{2} \sec ^2\left(\frac{\pi}{8}\right)=\frac{\sqrt{2}}{\sqrt{2}+1}$
$ f ^{\prime}\left(\frac{\pi}{4}\right)=\sqrt{2} f \left(\frac{\pi}{4}\right)$
A
$\frac{1}{8}$
B
$\frac{3}{4}$
C
$\frac{1}{4}$
D
$\frac{3}{8}$
Solution
$ \frac{d y}{d x}+2 y \tan x=\sin x$
I.F $=e^{\int 2 \tan x d x}=e^{\ln (\sec x)^2}=\sec ^2 x $
$y\left(\sec ^2 x\right)=\int \sin x \sec ^2 x d x+C$
$ y \cdot \sec ^2 x=\sec x+C $
Put $ x=\frac{\pi}{3}, y=0$
$ y=\cos x-2 \cos ^2 x$
$=\frac{1}{8}-2\left(\cos x-\frac{1}{4}\right)^2$
$\therefore y_{\max }=\frac{1}{8}$
A
$\frac{9}{2}$
B
$\frac{3 \sqrt{17}}{2}$
C
$\frac{3 \sqrt{17}}{4}$
D
$9$
Solution
$ ( x -1)^2+( y -2)^2+( x +2)^2+( y -1)^2=14$
$\Rightarrow x ^2+ y ^2+ x -3 y -2=0$
Put $ x =0$
$ \Rightarrow y ^2-3 y -2=0$
$ \Rightarrow y =\frac{3 \pm \sqrt{17}}{2}$
Put $ y =0 $
$ \Rightarrow x ^2+ x -2=0 $
$ ( x +2)( x -1)=0$
$\therefore A (-2,0), B (1,0), C \left(0, \frac{3+\sqrt{17}}{2}\right), D \left(0, \frac{3-\sqrt{17}}{2}\right) $
Area $=\frac{1}{2} \cdot 3 \cdot \sqrt{17}=\frac{3 \sqrt{17}}{2}$
A
$(25,10)$
B
$(20,12)$
C
$(30,8)$
D
$(15,13)$
Solution
Tangent at $(\alpha, \beta)$ has slope 1
$\beta^2=24 \alpha$
Equation of tangent $y \beta=12( x +\alpha), \frac{12}{\beta}=1$
$ \Rightarrow \alpha=6, \beta=12$
$ \therefore(\alpha+4, \beta+4)=(10,16)$
Normal at $(10,16)$ to $\frac{x^2}{36}-\frac{y^2}{144}=1$ is
$2 x+5 y=100$
A
$\sqrt{\frac{21}{2}}$
B
$\sqrt{\frac{9}{2}}$
C
$\sqrt{\frac{73}{2}}$
D
1
Solution
d.r's of the line $= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ 1 & -2 & 3\end{vmatrix} =\hat{i}-4 \hat{j}-3 \hat{k}$
$\therefore$ equation of line is
$\vec{ r }=\hat{ i }+2 \hat{ j }+4 \hat{ k }+\lambda(\hat{ i }-4 \hat{ j }-3 \hat{ k })$
Let $A (1,2,4)$ and $Pb (1+\lambda, 2-4 \lambda, 4-3 \lambda)$
$ \therefore \overrightarrow{ PA } \cdot(\hat{ i }-4 \hat{ j }-3 \hat{ k })=0 $
$ \lambda=\frac{1}{2} $
$\Rightarrow P \left(\frac{1}{2}, 2, \frac{-5}{2}\right)$
$ | AP |=\sqrt{\frac{21}{2}}$
A
$\frac{15}{2}$
B
8
C
$\frac{13}{2}$
D
7
Solution
$ \vec{a} \times \vec{b}=(1-\alpha) \hat{i}+\left(\alpha^2-2\right) \hat{j}+(\alpha-2) \hat{k}$
Projection of $ \vec{a} \times \vec{b} \text { on }-\hat{i}+2 \hat{j}-2 \hat{k} $
$ =\frac{(\vec{a} \times \vec{b}) \cdot(-\hat{i}+2 \hat{j}-2 \hat{k})}{3}=30$
$ \Rightarrow 2 \alpha^2-\alpha-91=0$
$ \Rightarrow \alpha=7,-\frac{13}{2}$
A
$\frac{5}{9}$
B
$\frac{64}{81}$
C
$\frac{16}{27}$
D
$\frac{145}{243}$
Solution
$ n p =\alpha ....$ (1)
$ npq =\alpha / 3.....$(2)
From (1) & (2)
$q =1 / 3 \& p =2 / 3 $
$ { }^{ n } C _1 q ^{ n -1} p ^1=\frac{4}{243}$
$ \frac{ n }{3^{ n }}=\frac{2}{243}$
$ n =6$
$P (4 \text { or } 5)$
$={ }^6 C _4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^2+{ }^6 C _5\left(\frac{2}{3}\right)^5 \cdot\left(\frac{1}{3}\right)^0 $
$ =\frac{16}{27}$
A
$\frac{2}{3}$
B
$\frac{5}{3}$
C
$\frac{5}{4}$
D
1
Solution
$ 0 \leq P \left( E _i\right) \leq 1 \text { for } i =1,2,3 $
$ \Rightarrow-2 / 3 \leq p \leq 1 $
$ E _1 \& E _2 \& E _3 $ are mutually exclusive
$ P \left( E _1\right)+ P \left( E _2\right)+ P \left( E _3\right) \leq 1$
$\Rightarrow 2 / 3 \leq p \leq 1 $
$p _1=1, p _2=2 / 3 $
$ p _1+ p _2=5 / 3$
A
0
B
$-2$
C
$-4$
D
12
Solution
$ 8^{2 \sin ^2 \theta}+8^{2-2 \sin ^2 \theta}=16 $
$ y +\frac{64}{ y }=16$
$ \Rightarrow y =8$
$ \Rightarrow \sin ^2 \theta=1 / 2$
$ n ( S )+\displaystyle\sum_{\theta \in S } \frac{1}{\cos (\pi / 4+2 \theta) \sin (\pi / 4+2 \theta)}$
$ =4+(-2) \times 4=-4$
A
1
B
2
C
$\frac{1}{4}$
D
$\frac{5}{4}$
Solution
$\tan \left(2\left(\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}\right)+\tan ^{-1}\left(\frac{1}{2}\right)\right) $
$ =\tan \left[2 \tan ^{-1}\left(\frac{1}{3}\right)+\tan ^{-1}\left(\frac{1}{2}\right)\right] $
$ =2$
A
a tautology
B
a contradiction
C
equivalent to $(p \Rightarrow q) \wedge q$
D
equivalent to $( p \Rightarrow q ) \wedge p$
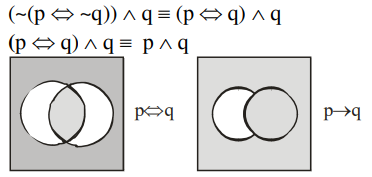
Answer: 272
Solution
$ ( px - q )^2+( qx - r )^2=0 $
$ \Rightarrow x =\frac{ q }{ p }=\frac{ r }{ q }=-4$
$ \Rightarrow \frac{ q ^2+ r ^2}{ p ^2}=272$
Answer: 180
Solution
$3 \times \frac{5 !}{2 ! 2 !}+\frac{5 !}{3 ! \times 2 !}+\frac{5 !}{2 !}+\frac{5 !}{3 !}=180$
Answer: 6993
Solution
$ S _{11}=3[101+102+\ldots \ldots+121] $
$ =\frac{3}{2}(222) \times 21=6993$
Answer: 3
Solution
$ x^5\left(x^3-x^2-x+1\right)+x\left(3 x^3-4 x^2-2 x+4\right)-1 =0$
$\Rightarrow(x-1)^2(x+1)\left(x^5+3 x-1\right)=0$
Let $ f(x)=x^5+3 x-1 $
$ f^{\prime}(x)>0 \forall x \in R$
Hence $3$ real distinct roots.
Answer: 23
Solution
Since coefficient of $x$ is $-3$
$ \Rightarrow{ }^{ p } C _1-{ }^{ q } C _1=-3$
$\Rightarrow p - q =-3 .....$(1)
Comparing coefficients of $x ^2$
$ -{ }^{ p } C _1{ }^{ q } C _1+{ }^{ p } C _2+{ }^{ q } C _2=-5 .......$(2)
$ - pq +\frac{ p ( p -1)}{2}+\frac{ q ( q -1)}{2}=-5$
Solving (1) and (2)
$p =8, q =11$
Coefficient of $x ^3$ is
$ -{ }^{ q } C _3+{ }^{ p } C _3+{ }^{ p } C _1{ }^{ q } C _2-{ }^{ p } C _2{ }^{ q } C _1 $
$=-{ }^{11} C _3+{ }^8 C _3+{ }^8 C _1{ }^{11} C _2-{ }^8 C _2{ }^{11} C _1 $
$=23$
Answer: 24
Solution
Let $I _1=\int\limits_0^1\left(1- x ^{ n }\right)^{2 n } dx$,
$I_2=\int\limits_0^1\left(1-x^n\right)^{2 n+1} d x$
$I_2=\int\limits_0^1\left(1-x^n\right)^{2 n+1} \cdot 1 d x$
$=\left.\left(1-x^n\right)^{2 n+1} \cdot x\right|_0 ^1-\int\limits_0^1(2 n+1)\left(1-x^n\right)^{2 n}\left(-n x^{n-1}\right) x d x$
$I_2=-n(2 n+1)\left\{I_2-I_1\right\} $
$\left(2 n^2+n+1\right) I_2=n(2 n+1) I_1 $
$\frac{I_1}{I_2}=\frac{2 n^2+ n +1}{ n (2 n +1)}=\frac{1177}{ n (2 n +1)} $
$\Rightarrow 2 n ^2+ n -1176=0 \Rightarrow n =24$
Answer: 6
Solution
$ x^4=3 y x \cdot y^{\prime}-3 y^2$
$ \Rightarrow 3 x y \frac{d y}{d x}=3 y^2+x^4 $
Put $ y^2=t, y \frac{d y}{d x}=\frac{1}{2} \frac{d t}{d x} $
$ \frac{d t}{d x}-\frac{2}{x} t=\frac{2}{3} x^3$
$ \therefore \frac{t}{x^2}=\frac{x^2}{3}+C $
$ \Rightarrow \frac{y^2}{x^2}=\frac{x^2}{3}-2$
Put $(3,3), C=-2$
$ \therefore \frac{y^2}{x^2}=\frac{x^2}{3}-2$
$3 y^2=x^4-6 x^2 $
$ x^4-6 x^2=1080$
$ \therefore x=6$
Answer: 3
Solution
Coordinates of $A (1,-2), B \left(\frac{15 a }{1-2 p }, \frac{-30 a }{1-2 p }\right)$ and orthocentre $H (2$, a)
Slope of $AH = p$
$a+2=p .....$(1)
Slope of $BH =-1$
$31 a -2 ab =15 a +4 p -2 .....$(2)
From (1) and (2)
$a =1 \& p =3$
Answer: 45
Solution

$ f^{\prime}(x)=4 x-\frac{1}{x} $
$ a=\frac{1}{2}$
Let $P \left( x _1, y _1\right)$ be any point on $y ^2=4 ax$
$\frac{1}{y_1}=\frac{3-y_1}{4-x_1} \Rightarrow y_1^2-6 y_1+8=0$
$ y_1=2,4 $
$ \Rightarrow P(8,4) $ as $P(2,2) $ rejected
Equation of normal at $ P$ .
$y-4=-4(x-8) $
$ \frac{x}{9}+\frac{y}{36}=1 $
$ \alpha=9, \beta=36 $
$\alpha+\beta=45$
Answer: 153





























