JEE Main Physics Question Paper with Solution 2023 January 25th Shift 2 - Evening
A
$20 V$
B
$16 V$
C
$8 V$
D
$12 V$
Solution

Induced emf across the ends $= Bv \ell$
$=2 \times 8 \times 1=16 V$
A
$8 \,m s^{-1}$
B
$20\, ms ^{-1}$
C
$25\, ms ^{-1}$
D
$40\, ms ^{-1}$
Solution
$ x =4 t ^2 $
$ v =\frac{ dx }{ dt }=8 t$
At $t =5 \sec$
$v =8 \times 5=40 \,m / s$
A
$\frac{3}{2} R$
B
$\frac{7}{2} R$
C
$\frac{9}{2} R$
D
$\frac{5}{2} R$
Solution
Diatomic gas molecules have three translational degree of freedom, two rotational degree of freedom & it is given that it has one vibrational mode so there are two additional degree of freedom corresponding to one vibrational mode, so total degree of freedom $=7$
$C _{ v }=\frac{ fR }{2}=\frac{7 R }{2}$
A
1.5S
B
3s
C
4s
D
2s
Solution

Let time from 0 to $A / 2$ is $t _1$
$\&$ from $A / 2$ to $A$ is $t _2$
then $\omega t _1=\pi / 6$
$ \omega t _2=\pi / 3 $
$ \frac{ t _1}{ t _2}=\frac{1}{2} $
$ t _2=2 t _1=2 \times 2=4 \sec$
A
$125$
B
5
C
25
D
625
Solution

$\because$ Volume of wire is constant in stretching
$V _{ i }= V _{ f } $
$ A _{ i } \ell_{ i }= A _{ f } \ell_{ f } $
$ A \ell= A ^{\prime}(5 \ell) $
$A ^{\prime}=\frac{ A }{5} $
$R _{ f }=\frac{\rho \ell_{ f }}{ A _{ f }}=\frac{\rho(5 \ell)}{\left(\frac{ A }{5}\right)} $
$=25\left(\frac{\rho \ell}{ A }\right) $
$=25 \times 5=125 \Omega$
A
$2.0$
B
$1.0$
C
$1.5$
D
$0.5$
Solution
$ \tau= K \theta $
$NiAB = K \theta $
$A =\frac{ K \theta}{ NiB }=\frac{4 \times 10^{-5} \times 0.05}{200 \times 10 \times 10^{-3} \times 0.01}$
On solving $A =10^{-4} m ^2=1 cm ^2$
A
Statenent I is correct but statement II is incorrect
B
Both Statement I and Statement II are incorrect
C
Statenent I is incorrect but statement II is correct
D
Both Statenent I and statement II are correct
Solution
Statement - I is correct
When P-N junction is formed an electric field is
generated form N-side to P-side due to which
barrier potential arises & majority charge carrier
can not flow through the junction due to barrier
potential so current is zero unless we apply
forward bias voltage.
A
$1:2$
B
$4: 1$
C
$2: 1$
D
$1:1$
Solution
$\text { Range }=\frac{ u ^2 \sin 2 \theta}{ g }$
Range for projection angle " $\alpha$ "
$R _1=\frac{ u ^2 \sin 2 \alpha}{ g }$
Range for projection angle " $\beta$ "
$R _2=\frac{ u ^2 \sin 2 \beta}{ g }$
$\alpha+\beta=90^{\circ} \text { (Given) }$
$\Rightarrow \beta=90^{\circ}-\alpha$
$ R _2=\frac{ u ^2 \sin 2\left(90^{\circ}-\alpha\right)}{ g } $
$ R _2=\frac{ u ^2 \sin \left(180^{\circ}-2 \alpha\right)}{ g }$
$ R _2=\frac{ u ^2 \sin 2 \alpha}{ g } $
$ \Rightarrow \frac{ R _1}{ R _2}=\frac{\left(\frac{ u ^2 \sin 2 \alpha}{ g }\right)}{\left(\frac{ u ^2 \sin 2 \alpha}{ g }\right)}=\frac{1}{1}$
A
$\frac{t_P}{100}=\frac{t_Q-180}{150}$
B
$\frac{t_Q}{150}=\frac{t_P-180}{100}$
C
$\frac{t_p}{180}-\frac{t_Q-40}{100}$
D
$\frac{t_Q}{100}=\frac{t_P-30}{150}$
Solution
$ \frac{\text { reading on scale }-\text { Lower fixed point }}{\text { upper fixed po int-lower fixed point }}=\text { constant }$
$ \frac{t_p-30}{180-30}=\frac{t_Q-0}{100-0} $
$ \frac{t_p-30}{150}=\frac{t_Q}{100}$
A
A and D only
B
$B$ and $C$ only
C
$A$ and $C$ Only
D
C and Donly
Solution
$ F =\frac{ Gm _1 m _2}{ r ^2} $
$ \Rightarrow F \propto \frac{1}{ r ^2}$
$\Rightarrow F \propto m _1 m _2 $
$\Rightarrow $ This force provides centripetal force and acts towards sun
$\Rightarrow T ^2 \propto a ^3 \text { (Kepler's third law) }$
A
Both Statement I and Statement II are incorrect
B
Statement I is correct but statement II is incorrect
C
Both Statement I and statement II are correct
D
Statement I is incorrect but statement II is correct
Solution
Stopping potential $V _{ S }=\frac{ KE _{\max }}{ e }$
$V _{ S }=\frac{\frac{ hC }{\lambda}-\phi}{ e }$
Stopping potential does not depend on intensity or power of light used, it only depends on frequency or wavelength of incident light.
So both statements I and II are correct
A
A-III, B-IV, C-II, D-I
B
A-I, B-II, C-IV, D-III
C
A-III, B-II, C-I, D-IV
D
A-I, B-IV, C-III, D-II
A
$0.50$
B
$0.33$
C
$0.25$
D
$0.60$
Solution

$ F _1= mg \sin 45^{\circ}+ f = mg \sin 45^{\circ}+\mu N $
$ F _1=\frac{ mg }{\sqrt{2}}+\mu mg \cos 45^{\circ}$
$ F _1=\frac{ mg }{\sqrt{2}}(1+\mu)$

$F _2= mg \sin 45^{\circ}- f = mg \sin 45^{\circ}-\mu N$
$ =\frac{ mg }{\sqrt{2}}(1-\mu) $
$ F _1=2 F _2$
$ \frac{ mg }{\sqrt{2}}(1+\mu)=2 \frac{ mg }{\sqrt{2}}(1-\mu) $
$ 1+\mu=2-2 \mu $
$ \mu=1 / 3=0.33$
A
B and C Only
B
A. C, and D Only
C
B and D only
D
A and $D$ Only
Solution
Plane mirror forms erect, same sized, laterally inverted and virtual image of real object.
A
$\frac{1}{2} m g R_e$
B
$3 m g R_e$
C
$\frac{2}{3} m g R_e$
D
$\frac{1}{3} m g R_e$
Solution
$ U =\frac{- GM _{ e } m }{ r } $
$ U _{ i }=\frac{- GM _{ e } m }{ R _{ e }} $
$ U _{ f }=\frac{- GM _{ e } m }{\left( R _{ e }+ h \right)}=\frac{- GM _{ e } m }{ R _{ e }+2 R _{ e }}$
$\frac{- GM _{ e } m }{3 R _{ e }}$
Increase in internal energy $\Delta U = U _{ f }- U _{ i }$
$ =\frac{2}{3} \frac{ GM _{ e } m }{ R _{ e }} $
$\frac{2}{3} \frac{ GM _{ e }}{ R _{ e }^2} mR _{ e } $
$=\frac{2}{3} mgR _{ e }$
A
$x=-4 \,cm$
B
$x=4 \, cm$
C
$x=8 \,cm$
D
$x=6 \,cm$
Solution

$ E_P=\frac{K \times 10}{2^2}-\frac{K \times 40}{\left(x_0-2\right)^2}=0 $
$ \frac{1}{2}=\frac{2}{x_0-2}$
$x_0-2=4 $
$ x_0=6\, cm$
A
A-I, B-III, C-IV, D-II
B
A-I, B-II, C-III, D-IV
C
A-II, B-III, C-IV, D-I
D
A-III, B-I, C-II, D-IV
Solution
$Y =\frac{\text { Stress }}{\text { Strain }}=\frac{ F / A }{\Delta \ell / \ell}=\frac{\left[ MLT ^{-2}\right]}{\left[ L ^2\right]}=\left[ ML ^{-1} T ^{-2}\right] $
$ F =6 \pi \eta rv \Rightarrow \eta=\frac{ F }{6 \pi rv } $
$ {[\eta]=\frac{\left[ MLT ^{-2}\right]}{[ L ]\left[ LT ^{-1}\right]}=\left[ ML ^{-1} T ^{-1}\right]} $
$ E = hv \Rightarrow h =\frac{ E }{v}=\frac{\left[ ML ^2 T ^{-2}\right]}{\left[ T ^{-1}\right]}=\left[ ML ^2 T ^{-1}\right]$
Work function has same dimension as that of energy, so $[\phi]=\left[ ML ^2 T ^{-2}\right]$
A
A-I, B-II, C-IV, D-III
B
A-II, B-I, C-IV, D-III
C
A-I, B-II, C-III, D-IV
D
A-II, B-I, C-III, D-IV
Solution
$\Delta U = nC _{ v } \Delta T$
For isothermal process $T$ is constant
So $\Delta U =0$
$A \longrightarrow II$
Adiabatic process
$ \Delta Q = 0 $
$ \Delta Q =\Delta U +\Delta W $
$\Delta U =-\Delta W$
Work done by gas is positive
So $\Delta U$ is negative
$\text { B } \longrightarrow \text { I }$
For Isochoric process $\Delta W =0$
$C \longrightarrow IV$
For Isobaric process
$\Delta W = P \Delta V \neq 0$
$\Delta U = nC _{ V } \Delta T \neq 0$
Heat absorbed goes partly to increase internal energy and partly do work.
A
A-I, B-II, C-III, D-IV
B
A-IV, B-I, C-II, D-III
C
A-III, B-IV, C-I, D-II
D
A-II, B-III, C-IV, D-I
Solution
Gauss's Law of electrostatic
$\phi=\oint \vec{ E } \cdot d \vec{ s }=\frac{ q }{\epsilon_0}$
Faraday's law $\oint \vec{E} \cdot \vec{d l}=\frac{-d \phi_B}{d t}$
Gauss's law of magnetism $\oint \vec{ B } \cdot d \vec{ A }=0$
Ampere's Maxwell law
$\oint \vec{B} . d \vec{l}=\mu_0 i_C+\mu_0 \in_0 \frac{d \phi_E}{d t}$
Where $i _{ C }$ : Conduction current
$\epsilon_0 \frac{ d \phi_{ E }}{ dt }$ : Displacement current
A
D
B
B
C
A
D
$C$
Solution
$ \lambda=\frac{ hc }{\Delta E } $
$ \Delta E _{ A }=2.2\, eV $
$ \Delta E _{ B }=5.2\, eV $
$ \Delta E _{ C }=3\, eV $
$\Delta E _{ D }=10 \, eV$
$ \lambda_{ A }=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{2.2 \times 1.6 \times 10^{-19}} $
$ =\frac{12.41 \times 10^{-7}}{2.2} m $
$=\frac{1241}{2.2} nm =564\, nm$
$\lambda_{ B }=\frac{1241}{5.2} nm =238.65\, nm$
$ \lambda_{ C }=\frac{1241}{3} nm =413.66 \, nm $
$ \lambda_{ D }=\frac{1241}{10}=124.1 \, nm$
Answer: 1
Solution

$ E _{ eq }=\frac{\frac{12}{3}-\frac{6}{6}}{\frac{1}{3}+\frac{1}{6}} $
$ E _{ eq }=6 V$
$ r _{ eq }=2 \Omega $
$ R =4 \Omega$
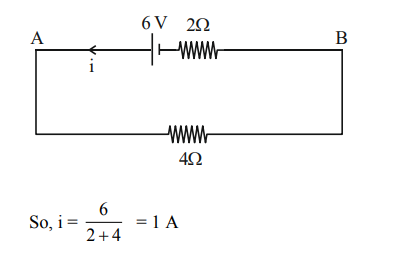
Answer: 30
Solution

$f =10\, cm$
$ \frac{1}{ v }-\frac{1}{ u }=\frac{1}{ f } $
$ \frac{1}{15}-\frac{1}{- u }=\frac{1}{10}$
$\Rightarrow \frac{1}{ u }=\frac{1}{10}-\frac{1}{15}$
On solving we get value of $u$ as $30 \,cm$.
Answer: 400
Solution

$ f_{\text {app }}=f\left(\frac{v}{v-v_s}\right)$
$ =320\left(\frac{330}{330-66}\right)$
$ =400 Hz $
Answer: 6
Solution

$=\frac{\in_0 A }{\left(\frac{ d }{3}+\frac{ d }{2}\right)}=\frac{6 \in_0 A }{5 d } $
$=\frac{6}{5} \times 5 \mu F =6 \mu F $
Answer: 68
Solution

Magnetic fields due to both wires will be perpendicular to each other.
$B_1=\frac{\mu_0 i_1}{2 \pi d } B_2=\frac{\mu_0 i _2}{2 \pi d } $
$ B _{ net }=\sqrt{ B _1^2+ B _2^2} \Rightarrow \frac{\mu_0}{2 \pi d } \sqrt{ i _1^2+ i _2^2} $
$\Rightarrow \frac{4 \pi \times 10^{-7}}{2 \pi \times(7 / \sqrt{2}) \times 10^{-2}} \times \sqrt{8^2+15^2}\left( d =\frac{7}{\sqrt{2}} cm \right)$
$ \Rightarrow 68 \times 10^{-6} T$
Answer: 5
Solution

$I _1=\frac{2}{5} m _1 R ^2+ m _1 R ^2 $
$I _1= m _1 R ^2\left(\frac{7}{5}\right) $
$ I _1=7 R ^2$

$ I _2=\frac{ m _2 R ^2}{4}+ m _2 R ^2 $
$ I _2=\frac{5}{4} m _2 R ^2 $
$ I _2=5 R ^2 $
$\frac{ I _2}{ I _1}=\frac{5}{7} $
$ x =5$
Answer: 1
Solution
Surface Tension $= T$
$R$ : Radius of bigger drop
$r$ : Radius of smaller drop
Volume will remain same
$ \frac{4}{3} \pi R ^3=1000 \times \frac{4}{3} \pi r ^3 $
$ R =10 r $
$ u _{ i }= T \cdot 4 \pi R ^2 $
$ u _{ f }= T \cdot 4 \pi r ^2 \times 1000$
$ \frac{ u _{ f }}{ u _{ i }}=\frac{1000 r ^2}{ R ^2}$
$\frac{ u _{ f }}{ u _{ i }}=\frac{10}{1}$
$\text { So, } x =1$
Answer: 2
Solution

$m _1 v _1= m _2 v _2 \Rightarrow \frac{ m _1}{ m _2}=\frac{2}{3}$
Since, Nuclear mass density is constant
$\frac{ m _1}{\frac{4}{3} \pi r _1^3}=\frac{ m _2}{\frac{4}{3} \pi r _2^3} $
$ \left(\frac{ r _1}{ r _2}\right)^3=\frac{ m _1}{ m _2}$
$ \frac{ r _1}{ r _2}=\left(\frac{2}{3}\right)^{\frac{1}{3}} $
$\text { So, } x=2$
Answer: 8
Solution
$ \cos \phi=\frac{R}{Z}=\frac{ R }{\sqrt{ R ^2+\left( X _{ C }- X _{ L }\right)^2}} $
$ \cos \phi=\frac{80}{\sqrt{(80)^2+(60)^2}} $
$ \cos \phi=\frac{80}{100} \Rightarrow \frac{8}{10}$
So, $x=8$
JEE Main Chemistry Question Paper with Solution 2023 January 25th Shift 2 - Evening
A
Both Statement I and Statement II are false
B
Both Statement I and Statement II are true
C
Statement I is false but Statement II is true
D
Statement I is true but Statement II is false
Solution
In froth floatation method a rotating paddle draws in air and stirs the pulp
A
A-III, B-IV, C-II, D-I
B
A-III, B-II, C-IV, D-I
C
A-I, B-IV, C-II, D-III
D
A-III, B-II, C-I, D-IV
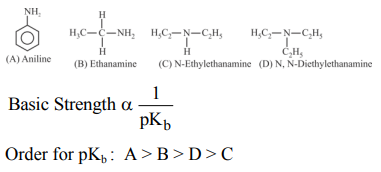
A
B and C only
B
A and C only
C
A and D only
D
A, B and C only
Solution
$B. \overset{\bullet}{Cl} + O_3 \rightarrow O_2 + Cl\overset{\bullet}{O}$
D. 'Blue baby' syndrome occurs due to the presence of excess of nitrate ions in water.
A
A-III, B-I, C-IV, D-II
B
A-III, B-IV, C-II, D-I
C
A-III, B-II, C-IV, D-I
D
A-III, B-IV, C-I, D-II
A
$A$ is not correct but $R$ is correct
B
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$
C
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
D
$A$ is correct but $R$ is not correct
Solution
The alkali metals and their salts impart characteristic colour to oxidizing flame.
A
A-IV, B-III, C-I, D-II
B
A-II, B-III, C-IV, D-I
C
A-IV, B-I, C-II, D-III
D
A-IV, B-III, C-II, D-I
Solution
Cobalt catalyst $\rightarrow$ Methanol production
Syn gas $\rightarrow$ Coal gasification
$\left( C _{(\text {Red hot coke })}+ H _2 O ( g ) \rightarrow CO + H _2\right)$
Nickel catalyst $\rightarrow$ Water gas production
Brine solution $\rightarrow$ Production
$($ aq. $NaCl ) \begin{pmatrix} H _2 \rightarrow \text { Cathode } \\ Cl _2 \rightarrow \text { anode }\end{pmatrix}$
A
A is not correct but $R$ is correct
B
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$
C
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
D
A is correct but $R$ is not correct
Solution
The oxide which form acid on dissolving in water is acidic oxide.
A
A-III, B-II, C-I, D-IV
B
A-II, B-III, C-IV, D-I
C
A-IV, B-I, C-III, D-II
D
A-III, B-I, C-II, D-IV
Solution
LIST I Coordination entity
LIST II Wavelength of light absorbed in nm
A
$\left[ CoCl \left( NH _3\right)_5\right]^{2+}$
I
535
B
$\left[ Co \left( NH _3\right)_6\right]^{3+}$
II
475
C
$\left[ Co ( CN )_6\right]^{3-}$
III
310
D
$\left[ Cu \left( H _2 O \right)_4\right]^{2+}$
IV
600
$E =\frac{ hc }{\lambda} \Rightarrow E \propto \frac{1}{\lambda}$
$\Rightarrow \Delta( CFSE ) \propto \frac{1}{\lambda_{\text {absorb }}} \propto \text { strength of ligand. }$
| LIST I Coordination entity | LIST II Wavelength of light absorbed in nm | ||
|---|---|---|---|
| A | $\left[ CoCl \left( NH _3\right)_5\right]^{2+}$ | I | 535 |
| B | $\left[ Co \left( NH _3\right)_6\right]^{3+}$ | II | 475 |
| C | $\left[ Co ( CN )_6\right]^{3-}$ | III | 310 |
| D | $\left[ Cu \left( H _2 O \right)_4\right]^{2+}$ | IV | 600 |
A
$1: 2$
B
$1: 1$
C
$3:1$
D
$2:1$
Solution
Assume : Mass of solvent $\approx$ Mass of solution
Case I :-
$0.25=\frac{W_1}{62} \times \frac{1000}{500}$
Case II :-
$ 0.25=\frac{ W _2}{62} \times \frac{1000}{250}$
$\frac{ W _1}{ W _2}=\frac{2}{1}$
A
$Rb$
B
$Na$
C
$Li$
D
$K$
Solution
Sodium have lowest oxidation potential in alkali metals. Hence it is weakest reducing agent among alkali metals.
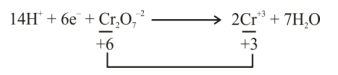
A
$+6$ to $+3$
B
$+6$ to $+2$
C
$+3$ to $+1$
D
$+2$ to $+1$
A
A-II, B-III, C-I, D-IV
B
A-III, B-I, C-IV, D-II
C
A-III, B-IV, C-I, D-II
D
A-IV, B-III, C-I, D-II
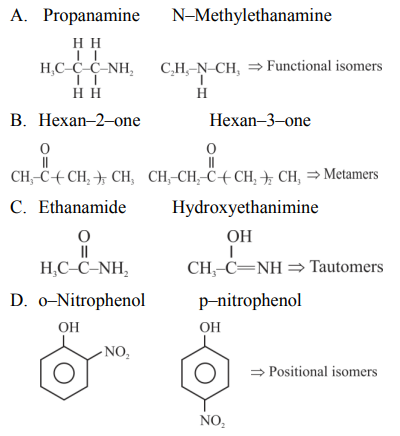
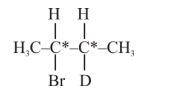
A
2 - Bromo - 1 - deuterobutane
B
2 - Bromo - 2 - deuterobutane
C
2 - Bromo - 3 - deuterobutane
D
2 - Bromo-1 - deutero - 2 - methylpropane
A
decreases by 3 units
B
decreases by 2 units
C
increases by 2 units
D
increases by 1000 units
Solution
$\Delta\left[ H ^{+}\right]=1000 $
$ \Delta pH =-\log \Delta\left[ H ^{+}\right]=-\log 10^3$
$ =-3$
A
Both Statement I and Statement II are correct
B
Statement I is correct but Statement II is incorrect
C
Statement I is incorrect but Statement II is correct
D
Both Statement I and Statement II are incorrect
Solution
Statement II : The corssed arrow symbolises the direction of the shift of electron density in the molecule.
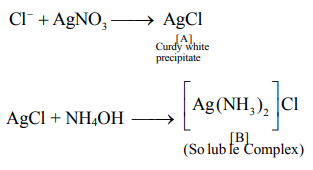
A
$H \left[ AgCl _3\right] \&\left( NH _4\right)\left[ Ag ( OH )_2\right]$
B
$H \left[ AgCl _3\right] \&\left[ Ag \left( NH _3\right)_2\right] Cl$
C
$AgCl \&\left[ Ag \left( NH _3\right)_2\right] Cl$
D
$AgCl \&\left( NH _4\right)\left[ Ag ( OH )_2\right]$
A
$Be < Si < Mg < K$
B
$K < Mg < Be < Si$
C
$Be < Si < K < Mg$
D
$Si < Be < Mg < K$
Solution
Metallic character increases down the group and decreases along the period.
A
$A$ is correct but $R$ is not correct
B
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$
C
A is not correct but $R$ is correct
D
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
Solution
Butylated hydroxyl anisole is an antioxidant.
Answer: 12
Solution
Element
Percentage
Mole
Mole ratio
C
85.8
$\frac{85.8}{12}=7.15$
1
H
14.2
$\frac{14.2}{1}=14.2$
2
Empirical formula $\left( CH _2\right)$
$14 \times n =84$
$n =6$
$\therefore$ Molecular formula $C _6 H _{12}$
| Element | Percentage | Mole | Mole ratio |
|---|---|---|---|
| C | 85.8 | $\frac{85.8}{12}=7.15$ | 1 |
| H | 14.2 | $\frac{14.2}{1}=14.2$ | 2 |
Answer: 3
Solution
Overall reaction :-
$ H _{2( g )}+ M _{\text {(aq) }}^{3+} > M _{\text {(aq) }}^{+}+2 H _{\text {(aq) }}^{+}$
$ E _{\text {Cell }}= E _{\text {Cathode }}^{ o }- E _{\text {anode }}^{\circ}-\frac{0.059}{2} \log \frac{\left[ M ^{+}\right] \times 1^2}{\left[ M ^{+3}\right] 1} $
$ 0.1115=0.2-\frac{0.059}{2} \log \frac{\left[ M ^{+}\right]}{\left[ M ^{+3}\right]} $
$ 3=\log \frac{\left[ M ^{+}\right]}{\left[ M ^{+3}\right]}$
$\therefore a =3$
Answer: 4
Solution
$\pi= iCRT$
$\pi \propto iC$
$A, B, D$ and $E$ have same value of osmatic pressure.
Answer: 925
Solution

$\Rightarrow 28=16.8+ x $
$x =11.2 L $
$ n _{ CH _4}=\frac{ PV }{ RT }=\frac{1 \times 5.6}{0.082 \times 298}=0.229 \text { mole }$
$ n _{ C _2 H _2}= \frac{11.2}{0.082 \times 298}=0.458 \text { mole } $
$\therefore \text { Heat evolved }=0.229 \times 900+0.458 \times 1400 $
$=206.1+641.2 $
$= 847.3 \,kJ$
Answer: 5
Solution
$p _{ x }, p _{ y }, p _{ z }, d _{ z ^2} \& d _{ x ^2- y ^2}$ are axial orbitals.
Answer: 2
Solution
‘$A$’ water vapours are absorbed by calcium
chloride.
C. As the adsorption proceeds, $\Delta H$ becomes less
and less negative
Answer: 2
Solution
$ t _{10 \%}=\frac{1}{ K } \ln \left(\frac{ a }{ a - x }\right)=\frac{1}{ K } \ln \left(\frac{100}{90}\right) $
$ t _{10 \%}=\frac{2.303}{ K }(\log 10-\log 9) $
$ t _{10 \%}=\frac{2.093}{ K } \times(0.04)$
Similarly
$ t _{90 \%}=\frac{1}{ K } \ln \left(\frac{100}{10}\right)$
$ t _{90 \%}=\frac{2.303}{ K } $
$ \frac{ t _{90 \%}}{ t _{10 \%}}=\frac{1}{0.04}=25 $
$e ^{ kt }=\frac{ a }{ a - x } $
$ \frac{ a - x }{ a }= e ^{- kt } $
$ 1-\frac{ x }{ a }= e ^{- kt } $
$ x = a \left(1- e ^{- kt }\right) $
$\alpha=\frac{ x }{ a }=\left(1- e ^{- kt }\right)$
Answer: 5
Solution
$\left[ Co \left( NH _3\right)_4 Cl _2\right] Cl \Rightarrow$ Gives 1 mole $AgCl$
$\left[ Ni \left( H _2 O \right)_6\right] Cl _2 \Rightarrow$ Gives 2 moles $AgCl$
$\left[ Pt \left( NH _3\right)_2 Cl _2\right] \Rightarrow$ Gives No $AgCl$
$\left[ Pd \left( NH _3\right)_4\right] Cl _2 \Rightarrow$ Gives 2 moles $AgCl$
Total number of moles of $AgCl =5$ mole.
JEE Main Mathematics Question Paper with Solution 2023 January 25th Shift 2 - Evening
A
$\frac{11}{6}-\log _e 4$
B
$\frac{11}{12}+\log _{ e } 4$
C
$\frac{11}{6}+\log _{ e } 4$
D
$\frac{11}{12}-\log _e 4$
Solution
$ I=16 \int\limits_1^2 \frac{d x}{x^3\left(x^2+2\right)^2}$
$ =16 \int\limits_1^2 \frac{d x}{x^3 x^4\left(1+\frac{2}{x^2}\right)^2}$
Let, $1+\frac{2}{x^2}=t \Rightarrow \frac{-4}{x^3} d x=d t$
$ I=-4 \int\limits_3^{\frac{3}{2}} \frac{d t}{\left(\frac{2}{t-1}\right)^2 t^2} $
$ I=-4 \int\limits_3^{\frac{3}{2}}\left(\frac{t-1}{2}\right)^2 \frac{d t}{t^2} $
$ I=-\frac{4}{4} \int\limits_3^{\frac{3}{2}}\left(1-\frac{2}{t}+\frac{1}{t^2}\right) d t$
$ I=-1\left[t-2 \ell n |t|-\frac{1}{t}\right]_3^{\frac{3}{2}}$
$ I=-1\left[\left(\frac{3}{2}-2 \ell n \frac{3}{2}-\frac{2}{3}\right)-\left(3-2 \ell n 3-\frac{1}{3}\right)\right]$
$ I=-1\left[2 \ell n 2-\frac{11}{6}\right]$
$I=\frac{11}{6}-\ell n 4$
A
${ }^{51} C _3-{ }^{45} C _3$
B
${ }^{52} C _4-{ }^{45} C _4$
C
${ }^{52} C _3-{ }^{45} C _3$
D
${ }^{51} C _4-{ }^{45} C _4$
Solution
$ \displaystyle\sum_{ k =0}^6{ }^{51- k } C _3$
$ ={ }^{51} C _3+{ }^{50} C _3+{ }^{49} C _3+\ldots+{ }^{45} C _3$
$ ={ }^{45} C _3+{ }^{46} C _3+\ldots . .+{ }^{51} C _3 $
$ ={ }^{45} C _4+{ }^{45} C _3+{ }^{46} C _3+\ldots . .+{ }^{51} C _3-{ }^{45} C _4 $
$ \left({ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r\right)$
$ ={ }^{52} C _4-{ }^{45} C _4 $
A
Only S 1 is true
B
Both S1 and S2 are false
C
Both S1 and S2 are true
D
Only S2 is true
Solution
Given, $A ^{ T }= A , B ^{ T }=- B , C ^{ T }=- C$
Let $M=A^{13} B^{26}-B^{26} A^{13}$
Then, $M^{ T }=\left( A ^{13} B ^{26}- B ^{26} A ^{13}\right)^{ T }$
$ =\left( A ^{13} B ^{26}\right)^{ T }-\left( B ^{26} A ^{13}\right)^{ T } $
$=\left( B ^{ T }\right)^{26}\left( A ^{ T }\right)^{13}-\left( A ^{ T }\right)^{13}\left( B ^{ T }\right)^{26} $
$ = B ^{26} A ^{13}- A ^{13} B ^{26}=- M$
Hence, $M$ is skew symmetric
Let, $N = A ^{26} C ^{13}- C ^{13} A ^{26}$
then, $N ^{ T }=\left( A ^{26} C ^{13}\right)^{ T }-\left( C ^{13} A ^{26}\right)^{ T }$
$=-( C )^{13}( A )^{26}+ A ^{26} C ^{13}= N$
Hence, $N$ is symmetric.
$\therefore$ Only S2 is true.
A
2
B
1
C
4
D
3
Solution
$f:\{1,2,3,4\} \rightarrow\{ a \in Z :| a | \leq 8\} $
$ f( n )+\frac{1}{ n } f ( n +1)=1, \forall n \in\{1,2,3\}$
$f( n +1)$ must be divisible by $n$
$f(4) \Rightarrow-6,-3,0,3,6$
$ f(3) \Rightarrow-8,-6,-4,-2,0,2,4,6,8 $
$ f(2) \Rightarrow-8, \ldots \ldots \cdots \cdots \cdots, 8 $
$ f(1) \Rightarrow-8, \ldots \ldots \ldots \ldots \ldots .8$
$\frac{f(4)}{3}$ must be odd since $f(3)$ should be even therefore 2 solution possible.
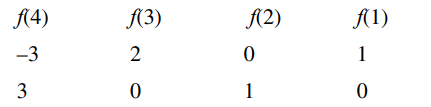
A
$\frac{107}{17}$
B
$\frac{73}{17}$
C
$-\frac{73}{17}$
D
$-\frac{107}{17}$
Solution
Let $A :(3,-4,2) C :(-2,-1,3)$
$\text { B : }(1,2,-1) \text { D : }(5,-2 \alpha, 4)$
$A, B, C, D $ are coplanar points, then
$ \Rightarrow\begin{vmatrix} 1-3 & 2+4 & -1-2 \\-2-3 & -1+4 & 3-2 \\5-3 & -2 \alpha+4 & 4-2\end{vmatrix}=0 $
$ \Rightarrow \alpha=\frac{73}{17}$
A
59
B
60
C
61
D
58
Solution
$ f( x )=2 x ^{ n }+\lambda$
$f(4)=133$
$ f(5)=255 $
$ 133=2 \times 4^{ n }+\lambda ...$(1)
$ 255=2 \times 5^{ n }+\lambda....$(2)
$ (2)-(1) $
$ 122=2\left(5^{ n }-4^{ n }\right) $
$ \Rightarrow 5^{ n }-4^{ n }=61 $
$ \therefore n =3 \& \lambda=5 $
Now, $ f(3)-f(2)=2\left(3^3-2^3\right)=38$
Number of Divisors is $1, 2, 19, 38 $; & their sum is $60$
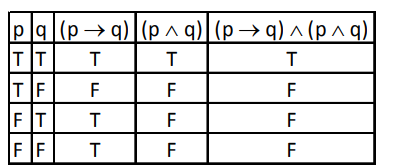
A
$\Delta=\wedge, \nabla=\wedge$
B
$\Delta=\vee, \nabla=\vee$
C
$\Delta=\vee, \nabla=\wedge$
D
$\Delta=\wedge, \nabla=\vee$
Solution
Given $( p \rightarrow q ) \Delta( p \nabla q )$
Option I $ \Delta=\wedge, \nabla=\vee$



Hence, it is tautology.
Option $4 \Delta=\wedge, \nabla=\wedge$
A
$4 y^2-18 y+3 x+18=0$
B
$4 y^2-18 y-3 x+18=0$
C
$4 y^2+18 y+3 x+18=0$
D
$4 y^2-18 y-3 x-18=0$
Solution
$ y^2=6 x \& y^2=4 a x$
$ \Rightarrow 4 a=6 \Rightarrow a=\frac{3}{2}$

$y = mx +\frac{3}{2 m } ;( m \neq 0)$
$h =\frac{6 m -3}{4 m ^2}, k =\frac{6 m +3}{4 m }$, Now eliminating $m$ and we get
$ \Rightarrow 3 h =2\left(-2 k ^2+9 k -9\right) $
$ \Rightarrow 4 y ^2-18 y +3 x +18=0$
A
$4 \sqrt{6}+\frac{44}{3}$
B
$4 \sqrt{6}-\frac{28}{3}$
C
$4 \sqrt{6}+\frac{28}{3}$
D
$4 \sqrt{6}-\frac{44}{3}$
Solution
$ 16\left(x^2+4 x\right)-\left(y^2-4 y\right)+44=0 $
$ 16(x+2)^2-64-(y-2)^2+4+44=0$
$ 16(x+2)^2-(y-2)^2=16 $
$\frac{(x+2)^2}{1}-\frac{(y-2)^2}{16}=1$

$ A=\int\limits_{-2}^{\sqrt{6}}\left(2-\left(x^2-4\right)\right) d x$
$ A=\int\limits_{-2}^{\sqrt{6}}\left(6-x^2\right) d x=\left(6 x-\frac{x^3}{3}\right)_{-2}^{\sqrt{6}}$
$ A=\left(6 \sqrt{6}-\frac{6 \sqrt{6}}{3}\right)-\left(-12+\frac{8}{3}\right) $
$A=\frac{12 \sqrt{6}}{3}+\frac{28}{3} $
$ A=4 \sqrt{6}+\frac{28}{3}$
A
72
B
120
C
6
D
12
Solution
Numbers between $5000 \& 10000$
Using digits $1,3,5,7,9$
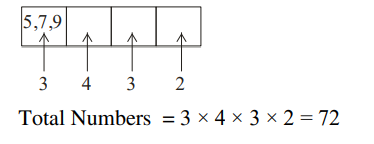
A
$\frac{3}{2}$
B
3
C
2
D
$\frac{5}{2}$
Solution
$ \frac{x+1}{1}=\frac{y}{\frac{1}{2}}=\frac{z}{\frac{-1}{12}} \text { and } \frac{x}{1}=\frac{y+2}{1}=\frac{z-1}{\frac{1}{6}} $
$ \Rightarrow \text { Shortest distance }=\frac{(\vec{ b }-\vec{ a }) \cdot(\vec{ p } \times \vec{ q })}{|\vec{ p } \times \vec{ q }|}$
$ \text { S.D. }=(-\hat{ i }+2 \hat{ j }-\hat{ k }) \cdot \frac{(\vec{ p } \times \vec{ q })}{|\vec{ p } \times \vec{ q }|}$
$ \left\{\vec{ p } \times \vec{ q } \equiv \begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 1 & \frac{1}{2} & \frac{-1}{12} \\ 1 & 1 & \frac{1}{6}\end{vmatrix}=\frac{1}{6} \hat{ i }-\frac{1}{4} \hat{ j }+\frac{1}{2} \hat{ k } \text { or } 2 \hat{ i }-3 \hat{ j }+6 \hat{ k }\right\} $
$\text { S.D. }=\frac{(-\hat{ i }+2 \hat{ j }-\hat{ k }) \cdot(2 \hat{ i }-3 \hat{ j }+6 \hat{ k })}{\sqrt{2^2+3^2+6^2}}=\left|\frac{-14}{7}\right|=2$
A
$(2,0)$
B
$(0,2)$
C
$(0,0)$
D
$(0,-2)$
Solution
$ ( z -2 i )(\overline{ z }+2 i )=4( z + i )(\overline{ z }- i )$
$ z \overline{ z }+4+2 i ( z -\overline{ z })=4( z \overline{ z }+1+ i (\overline{ z }- z )) $
$ 3 z \overline{ z }-6 i ( z -\overline{ z })=0$
$ x ^2+ y ^2-2 i (2 iy )=0$
$ x ^2+ y ^2+4 y =0$
A
$2 e^4+8$
B
11
C
8
D
10
Solution
$ \Rightarrow \displaystyle\lim _{x \rightarrow \frac{\pi^{+}}{2}} e^{\frac{\cot 6 x}{\cot 4 x}}=\displaystyle\lim _{x \rightarrow \frac{\pi^{+}}{2}} e ^{\frac{\sin 4 x \times \cos 6 x}{\sin 6 x \cdot \cos 4 x}}=e^{2 / 3}$
$ \Rightarrow \displaystyle\lim _{x \rightarrow \frac{\pi^{-}}{2}}(1+|\cos x|)^{\frac{\lambda}{\cos x} \mid}=e^\lambda $
$ \Rightarrow f(\pi / 2)=\mu$
For continuous function $\Rightarrow e ^{2 / 3}= e ^\lambda=\mu$
$\lambda=\frac{2}{3}, \mu= e ^{2 / 3}$
Now, $9 \lambda+6 \log _{ e } \mu+\mu^6- e ^{6 \lambda}=10$
A
$\begin{bmatrix}1 & -2023 i \\ 0 & 1\end{bmatrix}$
B
$\begin{bmatrix}1 & 0 \\ 2023 i & 1\end{bmatrix}$
C
$\begin{bmatrix}1 & 2023 i \\ 0 & 1\end{bmatrix}$
D
$\begin{bmatrix}1 & 0 \\ -2023 i & 1\end{bmatrix}$
Solution
$ AA ^{ T }=\begin{bmatrix} \frac{1}{\sqrt{10}} & \frac{3}{\sqrt{10}} \\ \frac{-3}{\sqrt{10}} & \frac{1}{\sqrt{10}}\end{bmatrix}\begin{bmatrix}\frac{1}{\sqrt{10}} & \frac{-3}{\sqrt{10}} \\ \frac{3}{\sqrt{10}} & \frac{1}{\sqrt{10}}\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} $
$ B ^2=\begin{bmatrix}1 & - i \\ 0 & 1\end{bmatrix} \begin{bmatrix}1 & - i \\ 0 & 1\end{bmatrix}=\begin{bmatrix} 1 & -2 i \\ 0 & 1\end{bmatrix} $
$ B ^3= \begin{bmatrix}1 & -3 i \\ 0 & 1\end{bmatrix}$
:
:
$ B ^{2023}=\begin{bmatrix}1 & -2023 i \\ 0 & 1\end{bmatrix} $
$ M = A ^{ T } B A $
$ M ^2= M \cdot M = A ^{ T } BA A ^{ T } BA = A ^{ T } B ^2 A$
$ M ^3= M ^2 \cdot M = A ^{ T } B ^2 AA ^{ T } BA = A ^{ T } B ^3 A $
:
:
$M ^{2023}=\ldots \ldots \ldots \ldots . . A ^{ T } B ^{2023} A$
$AM ^{2023} A ^{ T }= AA ^{ T } B ^{2023} AA ^{ T }= B ^{2023}$
$=\begin{bmatrix} 1 & -2023 i \\0 & 1\end{bmatrix}$
Inverse of $\left( AM ^{2023} A ^{ T }\right)$ is $\begin{bmatrix}1 & 2023 i \\ 0 & 1\end{bmatrix}$
A
$\frac{\gamma}{\alpha}=\frac{5}{8}$
B
$\frac{\beta}{\gamma}=-5$
C
$\frac{\alpha \beta}{\gamma}=\frac{4}{15}$
D
$\frac{\alpha}{\beta}=-8$
Solution
$L : \frac{ x +1}{2}=\frac{ y -1}{5}=\frac{ z +1}{-1}=\lambda$

Let foot of perpendicular is
$P (2 \lambda-1,5 \lambda+1,-\lambda-1) $
$ \overrightarrow{ PA }=(3-2 \lambda) \hat{ i }-(5 \lambda+1) \hat{ j }+(6+\lambda) \hat{ k }$
Direction ratio of line $\Rightarrow \vec{b}=2 \hat{i}+5 \hat{j}-\hat{k}$
$ \text { Now, } \Rightarrow \overrightarrow{ PA } \cdot \overrightarrow{ b }=0 $
$ \Rightarrow 2(3-2 \lambda)-5(5 \lambda+1)-(6+\lambda)=0 $
$ \Rightarrow \lambda=\frac{-1}{6}$
$ P (2 \lambda-1,5 \lambda+1,-\lambda-1) \equiv P (\alpha, \beta, \gamma)$
$ \Rightarrow \alpha=2\left(-\frac{1}{6}\right)-1=-\frac{4}{3} \Rightarrow \alpha=-\frac{4}{3} $
$ \Rightarrow \beta=5\left(-\frac{1}{6}\right)+1=\frac{1}{6} \Rightarrow \beta=\frac{1}{6}$
$ \Rightarrow \gamma=-\lambda-1=\frac{1}{6}-1 \Rightarrow \gamma=-\frac{5}{6}$
$\therefore$ Check options
A
3
B
5
C
4
D
2
Solution
Since,
$-\sqrt{2} \leq \sin x-\cos x \leq \sqrt{2}$
$ \therefore -2 \leq \sqrt{2}(\sin x-\cos x) \leq 2$
$(\text { Assume } \sqrt{2}(\sin x-\cos x)=k)$
$ -2 \leq k \leq 2 \ldots \text { (i) } $
$ f(x)=\log _{\sqrt{ m }}( k + m -2) $
$ \text { Given, } $
$ 0 \leq f( x ) \leq 2$
$ 0 \leq \log _{\sqrt{ m }}( k + m -2) \leq 2$
$ 1 \leq k + m -2 \leq m $
$ - m +3 \leq k \leq 2 \ldots \text { (ii) }$
From eq. (i) & (ii), we get $-m+3=-2$
$\Rightarrow m=5$
A
$\left(\frac{9}{2}, \infty\right)$
B
$\left(0, \frac{9}{2}\right)$
C
$\left(-\frac{9}{2}, \frac{9}{2}\right)$
D
$\left(-\infty, \frac{9}{2}\right)$
Solution
$ f(x)=2 x^3+(2 p-7) x^2+3(2 p-9) x-6 $
$ f^{\prime}(x)=6 x^2+2(2 p-7) x+3(2 p-9) $
$ f^{\prime}(0)<0$
$ \therefore 3(2 p -9)<0 $
$ p <\frac{9}{2}$
$p \in\left(-\infty, \frac{9}{2}\right) $
A
$3(\hat{i}-\hat{j}-\hat{k})$
B
$3(\hat{i}-\hat{j}+\hat{k})$
C
$3(\hat{i}+\hat{j}-\hat{k})$
D
$3(\hat{i}+\hat{j}+\hat{k})$
Solution
$\vec{ a } \times \vec{ b }=(\hat{ i }-\hat{ j })$
Taking cross product with $\vec{a}$
$ \Rightarrow \vec{a} \times(\vec{a} \times \vec{b})=\vec{a} \times(\hat{i}-\hat{j})$
$ \Rightarrow (\vec{a} \cdot \vec{b}) \vec{a}-(\vec{a} \cdot \vec{a}) \vec{b}=\hat{i}+\hat{j}+2 \hat{k}$
$ \Rightarrow \vec{a}-3 \vec{b}=\hat{i}+\hat{j}+2 \hat{k}$
$ \Rightarrow 2 \vec{a}-6 \vec{b}=2 \hat{i}+2 \hat{j}+4 \hat{k}$
$\Rightarrow \vec{a}-6 \vec{b}=3 \hat{i}+3 \hat{j}+3 \hat{k}$
A
is$-1$
B
is 0
C
is 1
D
does not exist
Solution
$ \frac{d y}{d t}+\alpha y=\gamma e^{-\beta t} $
$ \text { I.F. }=e^{\int \alpha d t}=e^{\alpha t} $
Solution $ \Rightarrow y \cdot e^{\alpha t}=\int \gamma c^{-\beta T } \cdot c^{\alpha t} d t $
$ \Rightarrow y e^{\alpha t}=\gamma \frac{e^{(\alpha-\beta) t}}{(\alpha-\beta)}+c $
$ \Rightarrow y=\frac{\gamma}{e^{\beta t}(\alpha-\beta)}+\frac{c}{e^{\alpha t}}$
So, $\displaystyle\lim _{t \rightarrow \infty} y(t)=\frac{\gamma}{\infty}+\frac{c}{\infty}=0$
A
16
B
2
C
8
D
4
Solution
$n(s)=36$
Given : $N -2, \sqrt{3 N }, N +2$ are in G.P.
$ 3 N =( N -2)( N +2)$
$ 3 N = N ^2-4 $
$ \Rightarrow N ^2-3 N -4=0$
$ ( N -4)( N +1)=0 \Rightarrow N =4 \text { or } N =-1 \text { rejected }$
$( Sum =4) \equiv\{(1,3),(3,1),(2,2)\} $
$ n ( A )=3$
$ P ( A )=\frac{3}{36}=\frac{1}{12}=\frac{4}{48} \Rightarrow k =4$
Answer: 31
Solution

$(1,1)(1,2)-(1,14) \Rightarrow 14$ pts.
If $x=2, y=\frac{27}{2}=13.5$
$(2,2)(2,4) \ldots(2,12) \Rightarrow 6$ pts.
If $x =3, y =\frac{51}{4}=12.75$
$(3,3)(3,6)-(3,12) \Rightarrow 4$ pts.
If $x=4, y=12$
$(4,4)(4,8) \Rightarrow 2$ pts.
If $x=5 \cdot y=\frac{45}{4}=11.25$
$(5,5),(5,10) \Rightarrow 2$ pts.
If $x=6, y=\frac{21}{2}=10.5$
$(6,6) \Rightarrow 1 pt$
If $x=7, y=\frac{39}{4}=9.75$
$(7,7) \Rightarrow 1 pt$
If $x=8, y=9$
$(8,8) \Rightarrow 1 pt$
If $x =9 y =\frac{33}{4}=8.25 \Rightarrow$ no pt.
Total $=31$ pts.
Answer: 20
Solution
$ \int\limits_{\frac{1}{3}}^3|\ell n x| d x=\int\limits_{\frac{1}{3}}^1(-\ell n x) d x+\int\limits_1^3(\ell n x) d x $
$=-[x \ell n x-x]_{1 / 3}^1+[x \ell n x-x]_1^3 $
$ =-\left[-1-\left(\frac{1}{3} \ell n \frac{1}{3}-\frac{1}{3}\right)\right]+[3 \ell n 3-3-(-1)] $
$ =\left[-\frac{2}{3}-\frac{1}{3} \ell n \frac{1}{3}\right]+[3 \ell n 3-2] $
$=-\frac{4}{3}+\frac{8}{3} \ell n 3$
$ =\frac{4}{3}(2 \ell n 3-1) $
$ =\frac{4}{3}\left(\ell n \frac{9}{ e }\right) $
$ \therefore m =4, n =3$
Now, $m ^2+ n ^2-5=16+9-5=20$
Answer: 6860
Solution
$7$ Red apple(RA),5 white apple(WA), 8 oranges $( O )$
5 fruits to be selected (Note:- fruits taken different)
Possible selections :- $(2 O , 1 RA , 2 WA )$ or $(2 O$,
$2 RA , 1 WA )$ or $(3 O , 1 RA , 1 WA )$
$\Rightarrow{ }^8 C _2{ }^7 C _1{ }^5 C _2+{ }^8 C _2{ }^7 C _2{ }^5 C _1+{ }^8 C _3{ }^7 C _1{ }^5 C _1 $
$ \Rightarrow 1960+2940+1960$
$ \Rightarrow 6860$
Answer: 3
Solution
$ m _{ PQ } \cdot m _{ QR }=-1$
$\Rightarrow \frac{10-2}{9+3} \times \frac{10-4}{9-\alpha}=-1 \Rightarrow \alpha=13 $
$ m _{ OP } \cdot m _{ QS }=-1 \Rightarrow m _{ QS }=-\frac{4}{7}$

Equation of QS
$ y-10=-\frac{4}{7}(x-9) $
$ \Rightarrow 4 x+7 y=106 \ldots .(1)$
$ m_{O R} \cdot m_{R S}=-1 \Rightarrow m_{R S}=-8$
Equation of RS
$y-4=-8(x-13) $
$ \Rightarrow 8 x+y=108...$(2)
Solving eq. (1) & (2)
$ x _1=\frac{25}{2} y _1=8 $
$S \left( x _1, y _1\right) \text { lies on } 2 x - ky =1 $
$ 25-8 k =1$
$ \Rightarrow 8 k =24 $
$ \Rightarrow k =3$
Answer: 25
Solution
$ \cos 2 \theta \cdot \cos \frac{\theta}{2}=\cos 3 \theta \cdot \cos \frac{9 \theta}{2} $
$ \Rightarrow 2 \cos 2 \theta \cdot \cos \frac{\theta}{2}=2 \cos \frac{9 \theta}{2} \cdot \cos 3 \theta$
$ \Rightarrow \cos \frac{5 \theta}{2}+\cos \frac{3 \theta}{2}=\cos \frac{15 \theta}{2}+\cos \frac{3 \theta}{2} $
$ \Rightarrow \cos \frac{15 \theta}{2}=\cos \frac{5 \theta}{2} $
$\Rightarrow \frac{15 \theta}{2}=2 k \pi \pm \frac{5 \theta}{2}$
$ 5 \theta=2 k \pi \text { or } 10 \theta=2 k \pi$
$\theta=\frac{2 k \pi}{5} \theta=\frac{ k \pi}{5}$
$\therefore \theta=\left\{-\pi, \frac{-4 \pi}{5}, \frac{-3 \pi}{5}, \frac{-2 \pi}{5}, \frac{-\pi}{5}, 0, \frac{\pi}{5}, \frac{2 \pi}{5}, \frac{3 \pi}{5}, \frac{4 \pi}{5}, \pi\right\} $
$m =5, n =5 $
$ \therefore m \cdot n =25$
Answer: 7
Solution
$ (2023)^{2023} $
$ =(2030-7)^{2023} $
$=(35 K -7)^{2023} $
$={ }^{2023} C _0(35 K )^{2023}(-7)^0+{ }^{2023} C _1(35 K )^{2022}(-7)+\ldots .+ $
$ \ldots \cdots+{ }^{2023} C _{2022}(-7)^{2023} $
$ =35 N -7^{2023} . $
$ \text { Now },-7^{2023}=-7 \times 7^{2022}=-7\left(7^2\right)^{1011}$
$=-7(50-1)^{1011}$
$=-7\left({ }^{1011} C _0 50^{1011}-{ }^{1011} C _1(50)^{1010}+\ldots \ldots \cdot{ }^{1011} C _{1011}\right)$
$ =-7(5 \lambda-1)$
$=-35 \lambda+7$
$\therefore$ when $(2023)^{2023}$ is divided by 35 remainder is 7
Answer: 9
Solution
$E _1: \text { Smokers } $
$ P \left( E _1\right)=\frac{1}{4} $
$E _2: \text { non-smokers } $
$P \left( E _2\right)=\frac{3}{4}$
E : diagnosed with lung cancer
$ P\left(E / E_1\right)=\frac{27}{28} $
$ P\left(E / E_2\right)=\frac{1}{28}$
$P\left(E_1 / E\right)=\frac{P\left(E_1\right) P\left(E / E_1\right)}{P(E)}$
$ =\frac{\frac{1}{4} \times \frac{27}{28}}{\frac{1}{4} \times \frac{27}{28}+\frac{3}{4} \times \frac{1}{28}}=\frac{\not{27}^9}{\not{30}_{10}}=\frac{9}{10} $
$ K=9$
Answer: 18
Solution
$ \vec{ r }=(\hat{ i }+2 \hat{ j }+3 \hat{ k })+\lambda(\hat{ i }+\hat{ j }+\hat{ k }) \vec{ r }=\vec{ a }+\lambda \vec{ p } $
$ \vec{ r }=(+\hat{ i }-\hat{ j }+2 \hat{ k })+\mu(2 \hat{ i }-\hat{ j }) \vec{ r }=\vec{ b }+\mu \vec{ q }$
$ \vec{ p } \times \vec{ q }=\begin{vmatrix} \hat{ i } & \hat{ j } & \hat{ k } \\ 1 & 1 & 1 \\ 2 & -1 & 0\end{vmatrix}=\hat{ i }+2 \hat{ j }-3 \hat{ k } $
$ d =\left|\frac{(\vec{ b }-\vec{ a }) \cdot(\vec{ p } \times \vec{ q })}{|\vec{ p } \times \vec{ q }|}\right|$
$d =\left|\frac{(-3 \hat{ j }-\hat{ k }) \cdot(\hat{ i }+2 \hat{ j }-3 \hat{ k })}{\sqrt{14}}\right| $
$=\left|\frac{-6+3}{\sqrt{14}}\right|=\frac{3}{\sqrt{14}}$
$ \alpha=\frac{3}{\sqrt{14}}$
Now, $28 \alpha^2=\not{28} ^2 \times \frac{9}{\not{14}}=18$
Answer: 45
Solution

$\alpha+\beta=-60^{\frac{1}{4}} \& \alpha \beta= a$
Given $\alpha^4+\beta^4=-30$
$\Rightarrow\left(\alpha^2+\beta^2\right)^2-2 \alpha^2 \beta^2=-30$
$ \Rightarrow\left\{(\alpha+\beta)^2-2 \alpha \beta\right\}^2-2 a^2=-30$
$ \Rightarrow\left\{60^{\frac{1}{2}}-2 a \right\}^2-2 a ^2=-30$
$ \Rightarrow 60+4 a ^2-4 a \times 60^{\frac{1}{2}}-2 a ^2=-30$
$\Rightarrow 2 a ^2-4.60^{\frac{1}{2}} a +90=0$
Product $=\frac{90}{2}=45$
Answer: 3




















