JEE Advanced Question Paper with Solution JEE Advanced 2021 Paper 1

JEE Advanced Physics Question Paper with Solution JEE Advanced 2021 Paper 1

Q1. The smallest division on the main scale of a Vernier calipers is $0.1 \,cm$. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is

A

3.07 cm

B

3.11 cm

C

3.15 cm

D

3.17 cm

Solution

So, we have given,
$10 VSD =9 MSD \Rightarrow 1 VSD =\frac{9}{10} MSD$
Least count $=1 MSD -1 VSD =\left(1-\frac{9}{10}\right) MSD$
$\Rightarrow 0.1 MSD =0.1 \times 0.1=0.01 cm$
As ' $O$ ' of vernier scale lies before ' $O$ ' of the main scale,
Zero error $=-(10-6) \times($ Least Count $)=-4 \times 0.01=-0.04 cm$
Reading $=3.1+1 \times($ Least count $)=3.1+1 \times 0.01=3.11 cm$
Therefore, true diameter $=$ Reading $-$ Zero error
$ =3.11-(-0.04)=3.15 cm $

Q2. An ideal gas undergoes a four step cycle as shown in the $P-V$ diagram below. During this cycle, heat is absorbed by the gas in

A

steps 1 and 2

B

steps 1 and 3

C

steps 1 and 4

D

steps 2 and 4

Solution

$\Delta Q_{1}=n C_{p} \Delta T>0$
$\Delta Q_{2}=n C_{V} \Delta T<0$
$\Delta Q_{3}=n C_{p} \Delta T<0$
$\Delta Q_{4}=n C_{V} \Delta T>0$

Q3. An extended object is placed at point $O, 10 \,cm$ in front of a convex lens $L_1$ and a concave lens $L_2$ is placed $10\, cm$ behind it, as shown in the figure. The radii of curvature of all the curved surfaces in both the lenses are $20 \,cm$. The refractive index of both the lenses is $1.5$. The total magnification of this lens system is

A

0.4

B

0.8

C

1.3

D

1.6

Solution

$\frac{1}{ f _{1}}=(1.5-1)\left(\frac{1}{20}+\frac{1}{20}\right)=\frac{1}{20}$
$\frac{1}{ f _{2}}=(1.5-1)\left(-\frac{1}{20}-\frac{1}{20}\right)=-\frac{1}{20}$
So, $\frac{1}{ v }-\frac{1}{-10}=\frac{1}{20}$
So, $v =-20\, cm$
and $\frac{1}{v^{\prime}}-\frac{1}{-30}=\frac{1}{-20}$
So, $v^{\prime}=-12 \,cm$
So total magnification $=\left(\frac{-20}{-10}\right)\left(\frac{-12}{-30}\right)=0.8$

Q4. A heavy nucleus $Q$ of half-life $20$ minutes undergoes alpha-decay with probability of $60 \%$ and beta-decay with probability of $40 \%$. Initially, the number of $Q$ nuclei is $1000 $. The number of alpha-decay of $Q$ in the first one hour is

A

50

B

75

C

350

D

525

Solution

Total no. of decays in $60$ minutes
$=1000-1000\left(\frac{1}{2}\right)^{3}=875$
So, no. of $\alpha$-decay $=875 \times 0.6=525$

Q5. A projectile is thrown from a point $O$ on the ground at an angle $45^{\circ}$ from the vertical and with a speed $5 \sqrt{2} \,m / s$. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, $0.5\, s$ after the splitting. The other part, $t$ seconds after the splitting, falls to the ground at a distance $x$ meters from the point $O$. The acceleration due to gravity $g =10 \,m / s ^{2}$.
The value of $t$ is ____.

Answer: 0.50

Solution

After splitting $1^{\text {st }}$ mass takes $0.5 \,sec$ to reach ground.
Initial velocity is same for both mass at the highest point in vertical direction. Displacement and acceleration in vertical direction is also same
So, $2^{\text {nd }}$ mass will also take $0.5\, sec$ to reach ground.

Q6. A projectile is thrown from a point $O$ on the ground at an angle $45^{\circ}$ from the vertical and with a speed $5 \sqrt{2} \,m / s$. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, $0.5\, s$ after the splitting. The other part, $t$ seconds after the splitting, falls to the ground at a distance $x$ meters from the point $O$. The acceleration due to gravity $g =10 \,m / s ^{2}$.
The value of $x$ is ______.

Answer: 7.50

Solution

image
Velocity of projectile at highest point $5\, m / s \hat{ i }$
Since, there is no external force in horizontal direction so by conservation of momentum
$m (5)=\frac{ m }{2}(0)+\frac{ m }{2}( v )$
$\vec{ v }=10 \,m / s \hat{ i }$
Distance covered by second mass before landing = $\frac{\text { Range }}{2}+10(t)=7.5\, m$

Q7. In the circuit shown below, the switch $S$ is connected to position $P$ for a long time so that the charge on the capacitor becomes $q _{1}\, \mu C$. Then $S$ is switched to position $Q$. After a long time, the charge on the capacitor is $q _{2}\, \mu C$.
image
The magnitude of $q_1$ is ____.

Answer: 1.33

Solution

image
After long time we can replace the capacitor by open circuit.
image
$i$ current in circuit $=1 / 3$ ampere
$v _{ AB }=2-2\left(\frac{1}{3}\right)=\frac{4}{3}$ volt
So, $q _{1}= CV =\frac{4}{3} \mu C$

Q8. In the circuit shown below, the switch $S$ is connected to position $P$ for a long time so that the charge on the capacitor becomes $q _{1}\, \mu C$. Then $S$ is switched to position $Q$. After a long time, the charge on the capacitor is $q _{2}\, \mu C$.
image
The magnitude of $q_2$ is ____.

Answer: 0.67

Solution

image
After long time $i$ circuit $=\frac{2}{3}$ ampere
image
$v _{ AB }=2-2\left(\frac{2}{3}\right)=\frac{2}{3}$ volt
So, $q _{2}= CV =(1)\left(\frac{2}{3}\right)=\frac{2}{3} \mu C$

Q9. Two point charges $- Q$ and $+ Q / \sqrt{3}$ are placed in the $xy$-plane at the origin $(0,0)$ and a point $(2,0)$, respectively, as shown in the figure. This results in an equipotential circle of radius $R$ and potential $V=0$ in the $x y$-plane with its center at $(b, 0)$. All lengths are measured in meters.
image
The value of $R$ is _______ meter.

Answer: 1.73

Solution

image
Lets take two points $( a , 0)$ and $( C , 0)$ on equipotential circle.
Net potential at $( C , 0)=0$
$\frac{K(-q)}{C}+\frac{K q}{\frac{\sqrt{3}}{(C-2)}}=0$
$\frac{1}{C}=\frac{1}{\sqrt{3}(C-2)} $
$\Rightarrow \sqrt{3} C-2 \sqrt{3}=C$
$\Rightarrow (\sqrt{3}-1) C =2 \sqrt{3} $
$\Rightarrow C =\frac{2 \sqrt{3}}{\sqrt{3}-1}$
Potential net at $(a, 0)=0$
$\frac{K(-q)}{a}+\frac{K \frac{q}{\sqrt{3}}}{(2-a)}=0 $
$\Rightarrow \frac{1}{a}=\frac{1}{\sqrt{3}(2-a)} $
$\Rightarrow 2 \sqrt{3}-\sqrt{3} a=a $
$\Rightarrow a=\frac{2 \sqrt{3}}{1+\sqrt{3}}$
So, Radius $=\frac{C-a}{2}=\frac{\frac{2 \sqrt{3}}{\sqrt{3}-1}-\frac{2 \sqrt{3}}{\sqrt{3}+1}}{2}$
$=\sqrt{3}\left(\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}\right)=\sqrt{3}\left(\frac{\sqrt{3}+1-\sqrt{3}+1}{3-1}\right) $
Radius $=\sqrt{3}$

Q10. Two point charges $- Q$ and $+ Q / \sqrt{3}$ are placed in the $xy$-plane at the origin $(0,0)$ and a point $(2,0)$, respectively, as shown in the figure. This results in an equipotential circle of radius $R$ and potential $V=0$ in the $x y$-plane with its center at $(b, 0)$. All lengths are measured in meters.
image
The value of $b$ is _______ meter.

Answer: 3.00

Solution

$b = a +$ radius
$=\frac{2 \sqrt{3}}{\sqrt{3}+1}+\sqrt{3}=\frac{2 \sqrt{3}+3+\sqrt{3}}{1+\sqrt{3}}$
$=\frac{3 \sqrt{3}+3}{1+\sqrt{3}}=3$
Center $=(3,0)$

Q11. A horizontal force $F$ is applied at the centre of mass of a cylindrical object of mass $m$ and radius $R$, perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is $\mu$. The center of mass of the object has an acceleration $a$. The acceleration due to gravity is $g$. Given that the object rolls without slipping, which of the following statement(s) is(are) correct?

A

For the same F, the value of $a$ does not depend on whether the cylinder is solid or hollow

B

For a solid cylinder, the maximum possible value of $a$ is $2 \mu g$

C

The magnitude of the frictional force on the object due to the ground is always $\mu mg$

D

For a thin-walled hollow cylinder, $a=\frac{F}{2 m}$

Solution

image
$F - f = ma $
$ fR = I \alpha $ (about center of mass)
$ a = R \alpha$ (pure rolling)
For hollow cylinder $a=\frac{F}{2 m}, f=\frac{F}{2}$
For solid cylinder, $a=\frac{2 F}{3 m}, f=\frac{F}{3}$
Also for solid cylinder $\frac{F}{2} \leq \mu\, mg$
Therefore a $\leq 2\, \mu g$

Q12. A wide slab consisting of two media of refractive indices $n_{1}$ and $n_{2}$ is placed in air as shown in the figure. A ray of light is incident from medium $n _{1}$ to $n _{2}$ at an angle $\theta$, where $\sin \theta$ is slightly larger than $1 / n _{1}$. Take refractive index of air as $1$ . Which of the following statement(s) is(are) correct?

A

The light ray enters air if $n_{2}=n_{1}$

B

The light ray is finally reflected back into the medium of refractive index $n _{1}$ if $n _{2}< n _{1}$

C

The light ray is finally reflected back into the medium of refractive index $n_{1}$ if $n_{2}>n_{1}$

D

The light ray is reflected back into the medium of refractive index $n_{1}$ if $n_{2}=1$

Solution

The ray diagram for the following conditions are
image
image
The light finally must reflected back in medium of refractive index $n_1$ for all values of $n_2$.

Q13. A particle of mass $M =0.2 \,kg$ is initially at rest in the $xy$-plane at a point $( x =-\ell, y =- h )$, where $\ell=10 \,m$ and $h =1\, m$. The particle is accelerated at time $t =0$ with a constant acceleration $a =10\, m / s ^{2}$ along the positive $x$-direction. Its angular momentum and torque with respect to the origin, in SI units, are represented by $\vec{ L }$ and $\vec{\tau}$ respectively. $\hat{ i }, \hat{ j }$ and $\hat{ k }$ are unit vectors along the positive $x , y$ and $z$-directions, respectively. If $\hat{k}=\hat{i} \times \hat{j}$ then which of the following statement(s) is(are) correct?

A

The particle arrives at the point $(x=\ell, y=-h)$ at time $t=2 s$.

B

$\vec{\tau}=2 \hat{k}$ when the particle passes through the point $(x=\ell, y=-h)$

C

$\vec{ L }=4 \hat{ k }$ when the particle passes through the point $( x =\ell, y =- h )$

D

$\vec{\tau}=\hat{k}$ when the particle passes through the point $(x=0, y=-h)$

Solution

Time taken to reach from $(-\ell,- h )$ to $(\ell,- h )$ is given by
$2 \ell=\frac{1}{2} at ^{2} $
$20=\frac{1}{2}(10) t ^{2} $
$ t =2\, sec $
$\vec{ L }= mvh \hat{ k }= math \hat{ k }$
$\vec{ L }=(0.2)(10) 2(1) \hat{ k }=4 \hat{ k }$ [ when particle passes through $ (\ell,- h )] $
$\vec{\tau}=\frac{ d \vec{ L }}{ dt }= mah \hat{ k }=(0.2)(10)(1) \hat{ k }=2 \hat{ k } $ (always)

Q14. Which of the following statement(s) is(are) correct about the spectrum of hydrogen atom?

A

The ratio of the longest wavelength to the shortest wavelength in Balmer series is $9 / 5$

B

There is an overlap between the wavelength ranges of Balmer and Paschen series

C

The wavelength of Lyman series are given by $\left(1+\frac{1}{ m ^{2}}\right) \lambda_{0}$, where $\lambda_{0}$ is the shortest wavelength of Lyman series and $m$ is an integer

D

The wavelength ranges of Lyman and Balmer series do not overlap

Solution

For hydrogen atom, $z =1$
$\frac{1}{\lambda}= R \left(\frac{1}{ n _{1}^{2}}-\frac{1}{ n _{2}^{2}}\right)$,
where $R =1.0973 \times 10^{7} m ^{-1}$
$=1.1 \times 10^{7} m ^{-1}=$ Rydberg constant.
For the Lyman series, $n _{1}=1$ and $n _{2}=2,3,4, \ldots \ldots \infty$
$\frac{1}{\lambda}= R \left(1-\frac{1}{ n _{2}^{2}}\right) $
$\lambda=\lambda_{\max }, $ when $ n _{2}=2$
$\frac{1}{\lambda_{\max }}=\frac{3 R }{4} $
$\Rightarrow \lambda_{\max }=\frac{4}{3 R }=121.5\, nm $
$\lambda=\lambda_{\min },$ when $n _{2}=\infty $
$\frac{1}{\lambda_{\min }}= R $
$\Rightarrow \lambda_{\min }=\frac{1}{ R }=91.1\, nm$
Also, $ \lambda=\left(\frac{ n _{2}^{2}}{ n _{2}^{2}-1}\right) \frac{1}{ R }=\left[1+\frac{1}{\left( n _{2}^{2}-1\right)}\right] \lambda_{0}$
$=\left(1+\frac{1}{ m ^{2}}\right) \lambda_{0} $
$\lambda=\left(1+\frac{1}{ m ^{2}}\right) \lambda_{0}$
where,
$ m ^{2}=\left( n _{2}^{2}-1\right)=$ an integer
$ m =\sqrt{ n _{2}^{2}-1}=$ not an integer
For the Balmer series, $n _{1}=2$ and $n _{2}=3,4,5,6,........, \infty$
$\frac{1}{\lambda}=R\left(\frac{1}{4}-\frac{1}{n_{2}^{2}}\right)$
$\lambda=\lambda_{\max }$, when $n _{2}=3$
$\frac{1}{\lambda_{\max }}=\frac{5 R }{36}$
$\lambda_{\max }=\frac{36}{5 R }=656.2\, nm$
$\lambda=\lambda_{\min }$, when $n _{2}=\infty$
$\Rightarrow \lambda_{\min }=\frac{4}{ R }=364.5\, nm$
Hence, for the Balmer series,
$\frac{\lambda_{\max }}{\lambda_{\min }}=\frac{36 / 5 R }{4 / R }=\frac{9}{5}$
For the Paschen series, $n _{1}=3$ and $n _{2}=4,5,6, \ldots \ldots ., \infty$
$\frac{1}{\lambda}= R \left(\frac{1}{9}-\frac{1}{ n _{2}^{2}}\right)$
$\lambda=\lambda_{\max }$, when $n _{2}=4$
$\frac{1}{\lambda_{\max }}= R \left(\frac{1}{9}-\frac{1}{16}\right)=\frac{7 R }{144}$
$\Rightarrow \lambda_{\max }=\frac{144}{7 R }=1874.7 \,nm$
$\frac{1}{\lambda_{\max }}= R \left(\frac{1}{9}-\frac{1}{16}\right)=\frac{7 R }{144}$
$\Rightarrow \lambda_{\max }=\frac{144}{7 R }=1874.7\, nm$
$\lambda=\lambda_{\min }$, when $n _{2}=\infty$
$\frac{1}{\lambda_{\min }}=\frac{ R }{9}$
$ \Rightarrow \lambda_{\min }=\frac{9}{ R }=820.2\, nm$

Q15. A long straight wire carries a current, $I =2$ ampere. A semi-circular conducting rod is placed beside it on two conducting parallel rails of negligible resistance. Both the rails are parallel to the wire. The wire, the rod and the rails lie in the same horizontal plane, as shown in the figure. Two ends of the semi-circular rod are at distances $1 \,cm$ and $4 \,cm$ from the wire. At time $t =0$, the rod starts moving on the rails with a speed $v =3.0\, m / s$ (see the figure)
A resistor $R =1.4 \,\Omega$ and a capacitor $C _{0}=5.0\, \mu F$ are connected in series between the rails. At time $t =0, C _{0}$ is uncharged. Which of the following statement(s) is(are) correct? $\left[\mu_{0}=4 \pi \times 10^{-7} SI\right.$ units. Take $\left.\ell n 2=0.7\right]$

A

Maximum current through $R$ is $1.2 \times 10^{-6}$ ampere

B

Maximum current through $R$ is $3.8 \times 10^{-6}$ ampere

C

Maximum charge on capacitor $C_{0}$ is $8.4 \times 10^{-12}$ coulomb

D

Maximum charge on capacitor $C_{0}$ is $2.4 \times 10^{-12}$ coulomb

Solution

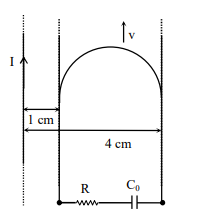
Emf induced across the semi-circular conducting rod.
$\varepsilon=\int\limits_{1}^{4} \frac{\mu_{0} I v d x}{2 \pi x}$
$=\frac{\mu_{0} I v}{2 \pi} \ln (4)=\frac{\mu_{0} I v}{\pi} \ln (2)$
Since the semi-circular conducting rod is moving with a constant speed
$v =3\, m / s$,
then $\varepsilon=\frac{\mu_{0} I v}{\pi} \ln (2)=$ constant
Maximum current through the resistor $R$ is
$i _{\max }=\frac{\varepsilon}{ R }=\frac{\mu_{0} Iv }{\pi R } \ln (2)$
$=\frac{4 \times 10^{-7} \times 2 \times 3 \times 0.7}{1.4}$
$=1.2 \times 10^{-6} $ ampere.
Maximum charge on the capacitor $C _{0}$ is
$q _{\max }= C _{0} \varepsilon= C _{0}\left(\frac{\mu_{0} Iv }{\pi} \ln (2)\right)$
$=5 \times 10^{-6} \times 4 \times 10^{-7} \times 2 \times 3 \times 0.7$
$=8.4 \times 10^{-12}$ coulomb.

Q16. A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta=45^{\circ} . P_{1}$ and $P_{2}$ are pressures at points $1$ and $2$, respectively located at the base of the tube. Let $\beta=\left(P_{1}-P_{2}\right) /(\rho g d)$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity. Which of the following statement(s) is(are) correct?

A

$\beta=0$ when $a=g / \sqrt{2}$

B

$\beta > 0$ when $a=g / \sqrt{2}$

C

$\beta=\frac{\sqrt{2}-1}{\sqrt{2}}$ when $a = g / 2$

D

$\beta=\frac{1}{\sqrt{2}}$ when $a = g / 2$

Solution

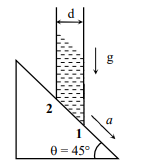
$\left(P_{1}-P_{2}\right) d s=\rho d s d \sqrt{2}(g \sin 45-a)$
$\left(P_{1}-P_{2}\right)=\rho d(g-a \sqrt{2})$
$\beta=\frac{\left(P_{1}-P_{2}\right)}{\rho g d}=\left(1-\frac{a \sqrt{2}}{g}\right)$
When $a=g / \sqrt{2}, \beta=0$
When $a=g / 2, \beta=\left(\frac{\sqrt{2}-1}{\sqrt{2}}\right)$

Q17. An $\alpha$-particle (mass $4 \,amu$ ) and a singly charged sulfur ion (mass $32\, amu$ ) are initially at rest. They are accelerated through a potential $V$ and then allowed to pass into a region of uniform magnetic field which is normal to the velocities of the particles. Within this region, the $\alpha$-particle and the sulfur ion move in circular orbits of radii $r_{\alpha}$ and $r_{s}$, respectively. The ratio $\left(r_{s} / r_{a}\right)$ is _____.

Answer: 4

Solution

$ r _{a} =\frac{\sqrt{2 m _{a} q _{a} V }}{ q _{a} B }$
$ r _{ S } =\frac{\sqrt{2 m _{ S } q _{ s } V }}{ q _{ s } B } $
$\frac{ r _{ S }}{ r _{a}} =\sqrt{\frac{ m _{ s }}{ q _{ S }} \frac{ q _{a}}{ m _{ a }}}=\sqrt{\left(\frac{32}{1}\right)\left(\frac{2}{4}\right)} $
$\frac{ r _{ s }}{ r _{a}} =4$

Q18. A thin rod of mass $M$ and length $a$ is free to rotate in horizontal plane about a fixed vertical axis passing through point $O$. A thin circular disc of mass $M$ and of radius $a / 4$ is pivoted on this rod with its center at a distance $a / 4$ from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity $\Omega$ and the disc rotating about its vertical axis with angular velocity $4\, \Omega$. The total angular momentum of the system about the point $O$ is $\left(\frac{ Ma ^{2} \Omega}{48}\right) n$. The value of $n$ is ______.

Answer: 49

Solution

Angular momentum of disc about $O$ is
$L _{ DO }= M \left(\frac{3 a }{4}\right)\left(\frac{3 a }{4}\right) \Omega+\frac{ M }{2}\left(\frac{ a }{4}\right)^{2}(4\, \Omega)$
Angular momentum of rod about $O$ is
$L _{ RO }=\frac{ Ma ^{2}}{3} \Omega$
So, $L _{0}= L _{ DO }+ L _{ Ro }=\frac{49}{48}\left( Ma ^{2} \Omega\right)$
So, $n =49$

Q19. A small object is placed at the center of a large evacuated hollow spherical container. Assume that the container is maintained at $0\, K$. At time $t =0$, the temperature of the object is $200 \,K$. The temperature of the object becomes $100 \,K$ at $t = t _{1}$ and $50\, K$ at $t = t _{2}$. Assume the object and the container to be ideal black bodies. The heat capacity of the object does not depend on temperature. The ratio $\left( t _{2} / t _{1}\right)$ is______.

Answer: 9

Solution

$- C \frac{ dT }{ dt }=\left( T ^{4}- T _{ s }^{4}\right)$
$\int\limits_{200}^{100} \frac{ dT }{ T ^{4}- T _{ s }^{4}}=\int\limits_{0}^{ t }-\frac{1}{ c } dt$
$-\frac{1}{3}\left[\frac{1}{ T ^{3}}\right]_{200}^{100}=-\frac{1}{ c }\left( t _{1}\right)$
$\Rightarrow \left[\frac{1}{(100)^{3}}-\frac{1}{(200)^{3}}\right]=\frac{3}{ c } t _{1}$
Similarly, $\left[\frac{1}{(50)^{3}}-\frac{1}{(200)^{3}}\right]=\frac{3}{ c } t _{2}$
$\frac{ t _{2}}{ t _{1}}=\frac{\left[\frac{1}{(50)^{3}}-\frac{1}{(200)^{3}}\right]}{\left[\frac{1}{(100)^{3}}-\frac{1}{(200)^{3}}\right]}=9$

JEE Advanced Chemistry Question Paper with Solution JEE Advanced 2021 Paper 1

Q1. The major product formed in the following reaction is

A

B

C

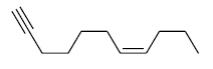
D

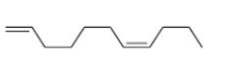
Solution

image
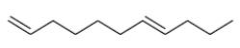
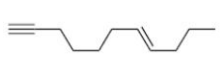
$Na$ in liquid $NH_3$ reduces non terminal alkyne into trans alkene.

Q2. Among the following, the conformation that corresponds to the most stable conformation of meso-butane-$2,3$-diol is

A

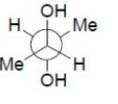
B

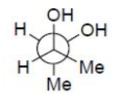
C

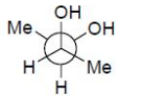
D

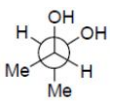
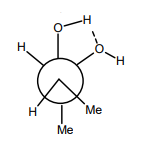
Solution

In option (B), given configuration represents meso - butane -$ 2, 3$-diol and due to intramolecular hydrogen
bonding, the gauche form is more stable.
Option (C) and (D) does not represent meso - isomer.

Q3. For the given close packed structure of a salt made of cation $X$ and anion $Y$ shown below (ions of only one face are shown for clarity), the packing fraction is approximately
(packing fraction $=\frac{\text { packing efficiency }}{100}$ )

A

0.74

B

0.63

C

0.52

D

0.48

Solution

Packing fraction $(f)=\frac{3 \times \frac{4}{3} \pi r_{+}^{3}+1 \times \frac{4}{3} \pi r_{-}^{3}}{a^{3}}$
$=\frac{1 \times \frac{4}{3} \pi\left[3\left(\frac{r_{+}}{r_{-}}\right)^{3}+1\right]}{\left(\frac{a}{r}\right)^{3}}$
Now $2 r _{-}= a$
$\therefore \frac{a}{r_{-}}=2$
Also, $\frac{r_{\text {土 }}}{r_{-}}=0.414$
So, $f=\frac{1 \times \frac{4}{3} \times 3.14\left[3 \times(0.414)^{3}+1\right]}{(2)^{3}}$
$=0.634 \approx 0.63$

Q4. The calculated spin only magnetic moments of $\left[ Cr \left( NH _{3}\right)_{6}\right]^{3+}$ and $\left[ CuF _{6}\right]^{3-}$ in BM, respectively, are (Atomic number of $Cr$ and $Cu$ are $24$ and $29$ , respectively)

A

3.87 and 2.84

B

4.90 and 1.73

C

3.87 and 1.73

D

4.90 and 2.84

Solution

$\left[ Cr \left( NH _{3}\right)_{6}\right]^{3+}$ has $d ^{3}$ configuration, so as per $CFT$,
$N =3$ and $\mu=\sqrt{3(3+2)}=3.87 \,BM$
$\left[ CuF _{6}\right]^{3-}$, has $d ^{8}$ configuration and weak field ligand.
So $N =2$ and $\mu=\sqrt{2(2+2)}=2.84\, BM$

Q5. For the following reaction scheme, percentage yields are given along the arrow:
image
$X\, g$ and $y \,g$ are mass of $R$ and $U$, respectively.
(Use : Molar mass (in $g \,mol^{-1})$ of $H, C$ and $O$ as $1, 12$ and $16$, respectively)
The value of $x$ is ______.

Answer: 1.62

Solution

image
image
Molar mass of $P = 40$
$\underset{(0.1 \text{mole})}{ P} \xrightarrow{75\%} \underset{(0.1 \times \frac{3}{4})}{Q}$
$\underset{(0.1 \times \frac{3}{4})}{3Q} \xrightarrow{40\%} \underset{(\frac{1}{3} \times 0.1 \times \frac{3}{4} \times 0.4)}{R}$
So, moles of $R = 0.01$ mole
Molar mass of $(R) = 162$
So, $x = 0.01 \times 162 = 1.62\,g$

Q6. For the following reaction scheme, percentage yields are given along the arrow:
image
$X\, g$ and $y \,g$ are mass of $R$ and $U$, respectively.
(Use : Molar mass (in $g \,mol^{-1})$ of $H, C$ and $O$ as $1, 12$ and $16$, respectively)
The value of $y$ is _______.

Answer:

Solution

Molar mass of ' $U$ ' $=122 \,g$ or $100 \,g$
$\underset{(0.1 \text { mole })}{ P } \xrightarrow{100 \%} \underset{(0.1 \text { mole })}{ S }$
$\underset{(0.1\text{mole})}{2S} \xrightarrow[(80\%)]{\text{Aldol condensation}} \underset{(\frac{0.1}{2} \times 0.8)}{T} \xrightarrow{80\%} \underset{(\frac{0.1}{2} \times 0.8\times .8)}{U}$
So, mass of '$U$' $=\frac{0.1}{2} \times 0.8 \times 0.8 \times 100=3.20\, gm$
Or
Mass of ' $U$ ' $=\frac{0.1}{2} \times 0.8 \times 0.8 \times 122=3.90\, gm$

Q7. For the reaction, $X (s) \rightleftharpoons Y (s)+ Z (g)$, the plot of $\ln \frac{p_{ Z }}{p^{0}}$ versus $\frac{10^{4}}{T}$ is given below (in solid line), where $p_{ z }$ is the pressure (in bar) of the gas $Z$ at temperature $T$ and $p^0=1$ bar.
image
(Given, $\frac{ d (\ln K)}{ d \left(\frac{1}{T}\right)}=-\frac{\Delta H^{0}}{R}$, where the equilibrium constant, $K=\frac{p_{z}}{p^{0}}$ and the gas constant, $R=8.314 \,J \,K ^{-1} mol ^{-1}$ )
The value of standard enthalpy, $\Delta H^{0}$ (in $kJ\, mol ^{-1}$ ) for the given reaction is ______.

Answer: 166.28

Solution

$ X ( s ) \rightleftharpoons Y ( s )+ Z ( g ) $
$ K _{ p }=\frac{ p _{ z }}{ p ^{0}}, $ also$ \Delta G ^{0}=- RT \ln k _{ p } $
$=- RT \ln \left(\frac{ p _{ z }}{ p ^{0}}\right)$
Now, $\Delta G ^{0}=\Delta H ^{0}- T \Delta S ^{0}$
$- RT$ kn $\left(\frac{ p _{z}}{ p ^{0}}\right)=\Delta H ^{0}- T \Delta S ^{0}$
$\ln \left(\frac{p_{z}}{p^{0}}\right)=-\left(\frac{\Delta H^{0}}{R}\right) \frac{1}{T}+\frac{\Delta S^{0}}{R}$ ....(1)
image
$(1) \Rightarrow \ln \left(\frac{p_{z}}{p^{0}}\right)=-\left(\frac{\Delta H^{0}}{10^{4} R}\right) \times \frac{10^{4}}{T}+\frac{\Delta S^{0}}{T} \ldots(2)$
Slope of the line $=-\frac{\Delta H ^{0}}{10^{4} R }$
$=\frac{[-7-(-3)]}{12-10}=-2$
$\therefore \Delta H ^{0}=2 R \times 10^{4}$
$=2 \times 8.314 \times 10^{-3} \times 10^{4}$
$=1.66 .28\, kJ \,mol ^{-1} K ^{-1}$

Q8. For the reaction, $X (s) \rightleftharpoons Y (s)+ Z (g)$, the plot of $\ln \frac{p_{ Z }}{p^{0}}$ versus $\frac{10^{4}}{T}$ is given below (in solid line), where $p_{ z }$ is the pressure (in bar) of the gas $Z$ at temperature $T$ and $p^0=1$ bar.
image
(Given, $\frac{ d (\ln K)}{ d \left(\frac{1}{T}\right)}=-\frac{\Delta H^{0}}{R}$, where the equilibrium constant, $K=\frac{p_{z}}{p^{0}}$ and the gas constant, $R=8.314 \,J \,K ^{-1} mol ^{-1}$ )
The value of $\Delta S^{0}$ (in $J\, K ^{-1} mol ^{-1}$ ) for the given reaction, at $1000\, K$ is ______.

Answer: 141.34

Solution

$ X ( s ) \rightleftharpoons Y ( s )+ Z ( g ) $
$ K _{ p }=\frac{ p _{ z }}{ p ^{0}}, $ also$ \Delta G ^{0}=- RT \ln k _{ p } $
$=- RT \ln \left(\frac{ p _{ z }}{ p ^{0}}\right)$
Now, $\Delta G ^{0}=\Delta H ^{0}- T \Delta S ^{0}$
$- RT$ kn $\left(\frac{ p _{z}}{ p ^{0}}\right)=\Delta H ^{0}- T \Delta S ^{0}$
$\ln \left(\frac{p_{z}}{p^{0}}\right)=-\left(\frac{\Delta H^{0}}{R}\right) \frac{1}{T}+\frac{\Delta S^{0}}{R}$ ....(1)
image
$(1) \Rightarrow \ln \left(\frac{p_{z}}{p^{0}}\right)=-\left(\frac{\Delta H^{0}}{10^{4} R}\right) \times \frac{10^{4}}{T}+\frac{\Delta S^{0}}{T} \ldots(2)$
Putting the value of $\Delta H ^{0}$ in equation (2), we get
$-3=-\left(\frac{2 R \times 10^{4}}{10^{4} R }\right) \times \frac{10^{4}}{7}+\frac{\Delta S ^{0}}{ R } $
$-3=-2 R \times \frac{10^{4}}{ T }+\frac{\Delta S ^{0}}{ R }$
$-3=-2 \times \frac{10^{4}}{1000}+\frac{\Delta S ^{0}}{ R } $
$-3=-20+\frac{\Delta S ^{0}}{ R }$
$\therefore \frac{\Delta S ^{0}}{ R }=17$
$\therefore \Delta S ^{0}=17 \times 8.314$
$=141.34 \,J\,K ^{-1} mol ^{-1}$

Q9. The boiling point of water in a $0.1$ molal silver nitrate solution (solution $A$ ) is $x ^{\circ} C$. To this solution $A$, an equal volume of $0.1$ molal aqueous barium chloride solution is added to make a new solution $B$. The difference in the boiling points of water in the two solutions $A$ and $B$ is $y \times 10^{-2}{ }^{\circ} C$.
(Assume: Densities of the solutions $A$ and $B$ are the same as that of water and the soluble salts dissociate completely.
Use: Molal elevation constant (Ebullioscopic Constant), $K _{ b }=0.5 \,K \,kg\, mol ^{-1}$;
Boiling point of pure water as $100^{\circ} C$.)
The value of $x$ is ______$^{\circ}C$.

Answer: 100.10

Solution

$0.1$ molal $AgNO _{3}$ (aq) solution
$ AgNO _{3} \longrightarrow Ag ^{+}( aq )+ NO _{3}{ }^{-}( aq )$
$ i =1+(2-1) \times 1=2(\alpha=1,$ given )
$\Delta T _{ b }= i \times k _{ b } \times m $
$\Delta T _{ b }=2 \times 0.5 \times 0.1=0.1$
So, boiling point of solution ' $A$ ' is $=100.10^{\circ} C = x$

Q10. The boiling point of water in a $0.1$ molal silver nitrate solution (solution $A$ ) is $x ^{\circ} C$. To this solution $A$, an equal volume of $0.1$ molal aqueous barium chloride solution is added to make a new solution $B$. The difference in the boiling points of water in the two solutions $A$ and $B$ is $y \times 10^{-2}{ }^{\circ} C$.
(Assume: Densities of the solutions $A$ and $B$ are the same as that of water and the soluble salts dissociate completely.
Use: Molal elevation constant (Ebullioscopic Constant), $K _{ b }=0.5 \,K \,kg\, mol ^{-1}$;
Boiling point of pure water as $100^{\circ} C$.)
The value of $|y|$ is ______.

Answer: 2.5

Solution

Let solution ' $B$ ' is prepared by mixing $1 \,L$ ( $=1000\, g$ ) of solution '$A$' with $1 \,L$ (= $1000\, g$ ) of solution of $BaCl _{2}$.
image
So, molality of new solution $=\left(\frac{ i _{1} \times m _{1}+ i _{2} \times m _{2}}{2}\right)$
$=\left(\frac{3 \times 0.05+3 \times 0.05}{2}\right) $
$=0.15 $
Now, Elevation of boiling point of solution ' $B$ ' be $\left(\Delta T_{b}{ }^{1}\right)$
$\Delta T _{ b }^{1}=0.15 \times k _{ b } $
$=0.15 \times \frac{1}{2} $
$=0.075$
Now, $T _{ b }{ }^{1}=100.075{ }^{\circ} C$
So, difference of boiling point of ' $A$ ' and ' $B$ '
$=100.10-100.075=0.025= y \times 10^{-2}$ (given)
So, $y =2.5$

Q11. Given:
image
The compound(s), which on reaction with $HNO _{3}$ will give the product having degree of rotation, $[\alpha]_{D}=-52.7^{\circ}$ is(are)

A

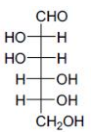
B

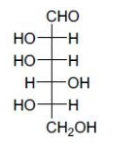
C

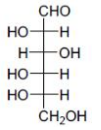
D

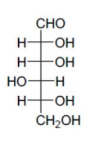
Solution

image
Since, we have to get the product $(x)$ of $(\alpha)_{0}=-52.7^{0}$, i.e. the enantiomer of above product. Which is only possible from (C) $\&$ (D).
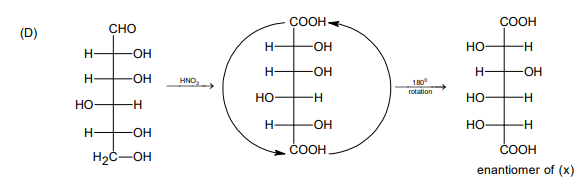
image
image

Q12. The reaction of $Q$ with PhSNa yields an organic compound (major product) that gives positive Carius test on treatment with $Na _{2} O _{2}$ followed by addition of $BaCl _{2}$. The correct option(s) for $Q$ is(are)

A

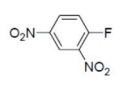
B

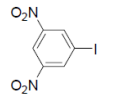
C

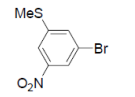
D

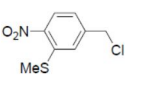
Solution

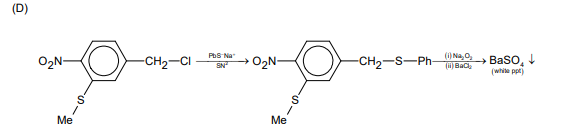
In option (B) and (C), $NO _{2}$ group (an EWG) is not present ortho or para position wrt the leaving group, so $ArSN ^{2}$ reaction will not be possible.
image
image

Q13. The correct statement(s) related to colloids is(are)

A

The process of precipitating colloidal sol by an electrolyte is called peptization.

B

Colloidal solution freezes at higher temperature than the true solution at the same concentration.

C

Surfactants form micelle above critical micelle concentration (CMC). CMC depends on temperature.

D

Micelles are macromolecular colloids.

Solution

(A) Process of precipitating colloidal solution by using an electrolyte is called "COAGULATION" and not peptisation.
(B) Since, molar mass of sol is much higher than true solutions, so magnitude of any colligative properties is smaller than true solutions.
$\left(\Delta T _{ f }\right)_{\text {sol }}<\left(\Delta T _{ f }\right)_{\text {true solution }}$
So, freezing point of sols $>$ freezing point of true solution.
So, option (B) is correct.
(C) Micells are formed greater than or equal to CMC and above KRAFT temperature.
So option (C) is also correct.
(D) Micelles are ASSOCIATED colloids and not Macromolecular colloids.

Q14. An ideal gas undergoes a reversible isothermal expansion from state I to state II followed by a reversible adiabatic expansion from state II to state III. The correct plot(s) representing the changes from state I to state III is(are)
( $p$ : pressure, $V$ : volume, $T$ : temperature, $H$ : enthalpy, $S$ : entropy)

A

B

C

D

Solution

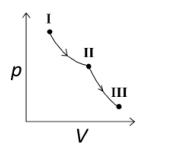
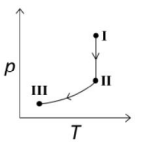
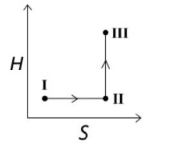
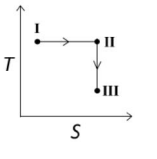
$(I) \xrightarrow[\text{expansion}]{\text{Reversible isotherm}} (II) \xrightarrow[\text{expansion}]{\text{Reversible adiabatic}} (III)$
So, the correct option is/are:
image
image
image
Reversible isothermal process is isoenthalpic while reversible adiabatic process is isoentropic.

Q15. The correct statement(s) related to the metal extraction processes is(are)

A

A mixture of $PbS$ and $PbO$ undergoes self-reduction to produce $Pb$ and $SO_2$.

B

In the extraction process of copper from copper pyrites, silica is added to produce copper silicate.

C

Partial oxidation of sulphide ore of copper by roasting, followed by self-reduction produces blister copper.

D

In cyanide process, zine powder is utilized to precipitate gold from $Na \left[ Au ( CN )_{2}\right]$.

Solution

(A) $PbS +2 PbO \xrightarrow{\text { self reduction }}3 Pb + SO _{2} \uparrow$
So option (A) is correct.
(B) In the extraction $Cu$ from copper pyrite $CuFeS _{2}$
$SiO _{2}$ is added to remove $FeO$ as slag $FeSiO _{3}$.
So option (B) is wrong.
(C) $\underset{\text { concentrated ore }}{ CuF e S _{2}} \xrightarrow{\text { roasting }} \underbrace{ Cu _{2} S + FeS }_{\text {(matte) }}+ SO _{2}$
$FeS + O _{2} \longrightarrow FeO + SO _{2}$
$Cu _{2} S + O _{2} \longrightarrow Cu _{2} O + SO _{2}$
$Cu _{2} S +2 Cu _{2} O \longrightarrow \underset{\text { (Bister copper) }}{6 Cu }+ SO _{2}$
So, option (C) is correct.
(D) $Zn +2 Na \left[ Au ( CN )_{2}\right] \rightarrow Na _{2}\left[ Zn ( CN )_{4}\right]+2 Au \downarrow$
So, option (D) is correct.

Q16. A mixture of two salts is used to prepare a solution $S$, which gives the following results:
$\text{White precipitate(s) only} \xleftarrow[\text{Room temperature}]{\text{Dilute} NaOH(aq)} \underset{\text{(aq solution of the salts)}}{S} \xrightarrow[\text{Room temperature}]{\text{Dilute } HCl(aq)}$ White precipitate(s) only
The correct option(s) for the salt mixture is(are)

A

$Pb \left( NO _{3}\right)_{2}$ and $Zn \left( NO _{3}\right)_{2}$

B

$Pb \left( NO _{3}\right)_{2}$ and $Bi \left( NO _{3}\right)_{3}$

C

$AgNO _{3}$ and $Bi \left( NO _{3}\right)_{3}$

D

$Pb \left( NO _{3}\right)_{2}$ and $Hg \left( NO _{3}\right)_{2}$

Solution

$Pb ( OH )_{2}, Zn ( OH )_{2}$ and $Bi ( OH )_{3}$ are white precipitates but $Hg ( OH )_{2}$ (unstable) is not. $PbCl _{2}$ is white $ppt$.
So, option (A), (B) and (C) are correct.

Q17. The maximum number of possible isomers (including stereoisomers) which may be formed on monobromination of $1$ -methylcyclohex-$1$-ene using $Br _{2}$ and UV light is_____.

Answer: 13

Q18. In the reaction given below, the total number of atoms having $sp^2$ hybridization in the major product $P$ is ______.

Answer: 12

Q19. The total number of possible isomers for $\left[ Pt \left( NH _{3}\right)_{4} Cl _{2}\right] Br _{2}$ is_____.

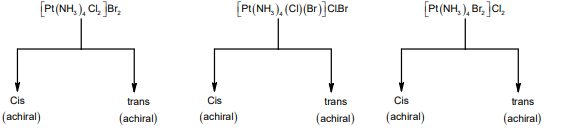
Answer: 6

Solution

Possible structural isomers are:

JEE Advanced Mathematics Question Paper with Solution JEE Advanced 2021 Paper 1

Q1. Consider a triangle $\Delta$ whose two sides lie on the $x$-axis and the line $x+y+1=0$. If the orthocentre of $\Delta$ is $(1,1)$, then the equation of the circle passing through the vertices of the triangle $\Delta$ is

A

$x^{2}+y^{2}-3 x+y=0$

B

$x^{2}+y^{2}+x+3 y=0$

C

$x^{2}+y^{2}+2 y-1=0$

D

$x^{2}+y^{2}+x+y=0$

Solution

image
Image of orthocentre about any side of the triangle lies on its circumcircle.
We can observe that
$x^{2}+y^{2}+x+3 y=0$ is satisfied by $(-1,0)$ and $(1,-1)$ both
So, option (B) is the correct choice

Q2. The area of the region $\left\{(x, y) ; \,\,0 \leq x \leq \frac{9}{4}, \,\, 0 \leq y \leq 1, \,\,x \geq 3 y, \,\,x+y \geq 2\right\}$ is

A

$\frac{11}{32}$

B

$\frac{35}{96}$

C

$\frac{37}{96}$

D

$\frac{13}{32}$

Solution

image
Area of shaded region
$=\frac{1}{2}\left(\frac{2}{3}+\frac{3}{4}\right) \frac{1}{4}+\frac{1}{2} \times \frac{2}{3} \times \frac{1}{2} $
$=\frac{11}{32}$

Q3. Consider three sets $E _{1}=\{1,2,3\}, F _{1}=\{1,3,4\}$ and $G _{1}=\{2,3,4,5\}$. Two elements are chosen at random, without replacement, from the set $E_{1}$ and let $S_{1}$ denote the set of these chose elements. Let $E_{2}=E_{1}-S_{1}$ and $F _{2}= F _{1} \cup S _{1}$. Now two elements are chosen at random, without replacement, from the set $F _{2}$ and let $S _{2}$ denote the set of these chosen elements.
Let $G _{2}= F _{1} \cup S _{2}$. Finally, two elements are chosen at random, without replacement, from the set $G _{2}$ and let $S _{3}$ denote the set of these chosen elements.
Let $E_{3}=E_{2} \cup S_{3}$. Given that $E_{1}=E_{3}$, let $p$ be the conditional probability of the event $S_{1}=\{1,2\}$. Then the value of $p$ is

A

$\frac{1}{5}$

B

$\frac{3}{5}$

C

$\frac{1}{2}$

D

$\frac{2}{5}$

Solution

$S_1$ $F_2 = F_1 \cup S_1$ $S_2$ $G_1 \cup S_2 = G_2$ $S_3$
(i) $\{1, 2\}$ $\{1, 2, 3, 4\}$ $\{1, x\}$ $\{1,2,3,4,5\}$ $\{1,2\}$
(ii) $\{2, 3\}$ $\{1,2,3,4\}$ $\{1,x\}$ $\{1,2,3,4,5\}$ $\{2,3\}$
$\{x, y\}$ (where $x$ and $y$ or $\{2,3,4,5\}$
(iii) $\{1,3\}$ $\{1,3,4\}$ $\{1, x\}$ are other than 1$)$ $\{1,2,3,4,5\}$ $\{1,3\}$
(i) $ P_{1}=\frac{{ }^{2} c_{2}}{{ }^{3} c_{2}} \cdot \frac{{ }^{3} c_{1}}{{ }^{4} c_{2}} \cdot \frac{{ }^{2} c_{1}}{{ }^{5} c_{2}}=\frac{1}{60}$
(ii) $ P_{2}=\frac{1}{3}\left(\frac{{ }^{3} c _{1}}{{ }^{4} c _{2}} \times \frac{{ }^{2} c _{2}}{{ }^{5} c _{2}}+\frac{{ }^{3} c _{2}}{{ }^{4} c _{2}} \times \frac{{ }^{2} c _{2}}{{ }^{4} c _{2}}\right)=\frac{2}{45}$
(iii) $ P_{3}=\frac{1}{{ }^{3} c_{1}} \times \frac{{ }^{2} c_{1}}{{ }^{3} c_{2}} \times \frac{{ }^{2} c_{2}}{{ }^{5} c_{2}}=\frac{1}{45}$
Conditional probability $=\frac{P_{1}}{P_{1}+P_{2}+P_{3}}=\frac{1}{5}$

Q4. Let $\theta_{1}, \theta_{2}, \ldots . ., \theta_{10}$ be positive valued angles (in radian) such that $\theta_{1}+\theta_{2}+\ldots . .+\theta_{10}=2 \pi$. Define the complex numbers $z_{1}=e^{i \theta_{1}}, z_{k}=z_{k-1} e^{i \theta_{k}}$ for $k=2,3, \ldots \ldots, 10$, where $i=\sqrt{-1}$. Consider the statements $P$ and $Q$ given below:
$P:\left|z_{2}-z_{1}\right|+\left|z_{3}-z_{2}\right|+\ldots .+\left|z_{10}-z_{9}\right|+\left|z_{1}-z_{10}\right| \leq 2 \pi $
$Q:\left|z_{2}^{2}-z_{1}^{2}\right|+\left|z_{3}^{2}-z_{2}^{2}\right|+\ldots . .+\left|z_{10}^{2}-z_{9}^{2}\right|+\left|z_{1}^{2}-z_{10}^{2}\right| \leq 4 \pi$

A

P is TRUE and Q is FALSE

B

Q is TRUE and P is FALSE

C

both P and Q are TRUE

D

both P and Q are FALSE

Solution

image
$\because z_{1}=e^{i \theta_{1}}$
So, $z_{2}=e^{i\left(\theta_{1}+\theta_{2}\right)}$
$z_{3}=e^{i\left(\theta_{1}+\theta_{2}+\theta_{3}\right)}$
:
$z _{10}= e ^{ i \left(\theta_{1}+\theta_{2}+\ldots \ldots+\theta_{10}\right)}= e ^{ i (2 \pi)}$
Sum of all the chord length $ < $ Circumference
So, $\sum\left|z_{2}-z_{1}\right| \leq 2 \pi$
Also, $2\left|z_{2}-z_{1}\right| \geq\left|z_{2}^{2}-z_{1}^{2}\right|$
Hence, $2\left(\left|z_{2}-z_{1}\right|+\ldots . .+\left|z_{10}-z_{1}\right|\right) \leq 2(2 \pi)=4 \pi$
So for, we have $P \leq 2 \pi$ and $Q \leq 4 \pi$

Q5. Three numbers are chosen at random, one after another with replacement, from the set $S =\{1,2,3, \ldots . ., 100\}$. Let $p _{1}$ be the probability that the maximum of chosen numbers is at least $81$ and $p _{2}$ be the probability that the minimum of chosen numbers is at most $40$ .
The value of $\frac{625}{4} p_{1}$ is _____.

Answer: 76.25

Solution

$P_{1}=1$ - (Probability that $3$ chosen numbers are less than $81$ )
$=1-\left(\frac{80}{100}\right)^{3}=1-\frac{64}{125}=\frac{61}{125}$
So, $\frac{625}{4}$
$P_{1}=\frac{625}{4} \times \frac{61}{125}=76.25$

Q6. Three numbers are chosen at random, one after another with replacement, from the set $S =\{1,2,3, \ldots . ., 100\}$. Let $p _{1}$ be the probability that the maximum of chosen numbers is at least $81$ and $p _{2}$ be the probability that the minimum of chosen numbers is at most $40$ .
The value of $\frac{125}{4} p_{2}$ is ______.

Answer: 24.5

Solution

$P_{2}=1$-(Probability that 3 chosen numbers are greater than 40 )
$=1-\left(\frac{60}{100}\right)^{3}=1-\left(\frac{3}{5}\right)^{3}=\frac{98}{125}$
So, $\frac{125}{4}$
$P_{2}=\frac{125}{4} \times \frac{98}{125}=24.5$

Q7. Let $\alpha, \beta$ and $\gamma$ be real numbers such that the system of linear equation
$x+2 y+3 z=\alpha$
$4 x+5 y+6 z=\beta $
$7 x+8 y+9 z=\gamma-1$
is consistent. Let $| M |$ represent the determinant of the matrix
$M=\begin{bmatrix}\alpha & 2 & \gamma \\\beta & 1 & 0 \\-1 & 0 & 1\end{bmatrix}$
Let $P$ be the plane containing all those ( $\alpha, \beta, \gamma$ ) for which the above system of linear equations is consistent, and $D$ be the square of the distance of the point $(0,1,0)$ from the plane $P$.
The value of $|M|$ is ________.

Answer: 1

Solution

$x+2 y+3 z=\alpha$
$4 x+5 y+6 z=\beta $
$7 x+8 y+9 z=\gamma-1$
Equation $(1)+(3)-(2)=0$. Equation $(2)$ provides
$\alpha+\gamma-1-2 \beta=0$
$|M|=\begin{vmatrix}\alpha & 2 & \gamma \\ \beta & 1 & 0 \\ -1 & 0 & 1\end{vmatrix}\left(C_{1} \rightarrow C_{1}+C_{3}\right)$
$=\begin{vmatrix}\alpha+\gamma & 2 & \gamma \\ \beta & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}\left(R_{1} \rightarrow R_{1}-2 R_{2}\right)$
$\begin{vmatrix}\alpha+\gamma-2 \beta & 0 & \gamma \\ \beta & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}=\begin{vmatrix}1 & 0 & \gamma \\ \beta & 1 & 0 \\ 0 & 0 & 1\end{vmatrix}=1$

Q8. Let $\alpha, \beta$ and $\gamma$ be real numbers such that the system of linear equation
$x+2 y+3 z=\alpha$
$4 x+5 y+6 z=\beta $
$7 x+8 y+9 z=\gamma-1$
is consistent. Let $| M |$ represent the determinant of the matrix
$M=\begin{bmatrix}\alpha & 2 & \gamma \\\beta & 1 & 0 \\-1 & 0 & 1\end{bmatrix}$
Let $P$ be the plane containing all those ( $\alpha, \beta, \gamma$ ) for which the above system of linear equations is consistent, and $D$ be the square of the distance of the point $(0,1,0)$ from the plane $P$.
The value of $D$ is _______.

Answer: 1.5

Solution

$x+2 y+3 z=\alpha$
$4 x+5 y+6 z=\beta $
$7 x+8 y+9 z=\gamma-1$
Equation $(1)+(3)-(2)=0$. Equation $(2)$ provides
$\alpha+\gamma-1-2 \beta=0$
Plane $P$ is $x-2 y+z-1=0$
$D=\left(\frac{|-2-1|}{\sqrt{1+4+1}}\right)^{2}=1.5$

Q9. Consider the lines $L _{1}$ and $L _{2}$ defined by
$L_{1}: x \sqrt{2}+y-1=0$ and $L_{2}: x \sqrt{2}-y+1=0$
For a fixed constant $\lambda$, let $C$ be the locus of a point $P$ such that the product of the distance of $P$ from $L _{1}$ and the distance of $P$ from $L_{2}$ is $\lambda^{2}$. The line $y=2 x+1$ meets $C$ at two points $R$ and $S$, where the distance between $R$ and $S$ is $\sqrt{270}$.
Let the perpendicular bisector of $RS$ meet $C$ at two distinct points $R ^{\prime}$ and $S ^{\prime}$. Let $D$ be the square of the distance between $R ^{\prime}$ and $S ^{\prime}$
The value of $\lambda^2$ is _____ .

Answer: 9

Solution

Locus $C=\left|\frac{(x \sqrt{2}+y-1)(x \sqrt{2}-y+1)}{\sqrt{3}}\right|=\lambda^{2}$
$2 x^{2}-(y-1)^{2}=\pm 3 \lambda^{2}$
for intersection with $y=2 x+1$
$2 x^{2}-(2 x)^{2}=\pm 3 \lambda^{2}$
$-2 x^{2}=-3 \lambda^{2}$ (taking $-$ ve sign )
$x=\pm \sqrt{\frac{3}{2}} \lambda$
Distance between $R$ and $S =2\left|\sqrt{\frac{3}{2}} \lambda\right| \sec \theta (\tan \theta$ is slope of line)
$=\sqrt{6}|\lambda| \sqrt{5}$
So, $\sqrt{30}|\lambda|=\sqrt{270}(\lambda=\pm 3)$
$\lambda^{2}=9$

Q10. Consider the lines $L _{1}$ and $L _{2}$ defined by
$L_{1}: x \sqrt{2}+y-1=0$ and $L_{2}: x \sqrt{2}-y+1=0$
For a fixed constant $\lambda$, let $C$ be the locus of a point $P$ such that the product of the distance of $P$ from $L _{1}$ and the distance of $P$ from $L_{2}$ is $\lambda^{2}$. The line $y=2 x+1$ meets $C$ at two points $R$ and $S$, where the distance between $R$ and $S$ is $\sqrt{270}$.
Let the perpendicular bisector of $RS$ meet $C$ at two distinct points $R ^{\prime}$ and $S ^{\prime}$. Let $D$ be the square of the distance between $R ^{\prime}$ and $S ^{\prime}$
The value of $D$ is _____

Answer: 77.14

Solution

Equation of perpendicular bisector $y=-\frac{1}{2} x+1$
For point of intersection $2 x^{2}-\frac{1}{4} x^{2}=\pm 3 \lambda^{2}$
$ x =\pm \sqrt{\frac{12}{7}} \lambda $ (taking + ve sign)
Distance $=\left|2 \cdot \sqrt{\frac{12}{7}} \cdot 3 \cdot \sec \theta\right|$
$=2 \cdot \sqrt{\frac{12}{7}} \cdot 3 \cdot \sqrt{\frac{5}{2}}$
$=3 \cdot \sqrt{\frac{60}{7}}$
$D =\frac{9 \times 60}{7}=77.14$

Q11. For any $3 \times 3$ matrix $M$, let $| M |$ denote the determinant of $M$. Let
$E=\begin{bmatrix}1 & 2 & 3 \\2 & 3 & 4 \\8 & 13 & 18\end{bmatrix}, P=\begin{bmatrix} 1 & 0 & 0 \\0 & 0 & 1 \\0 & 1 & 0\end{bmatrix}$ and $F=\begin{bmatrix} 1 & 3 & 2 \\ 8 & 18 & 13 \\ 2 & 4 & 3 \end{bmatrix}$
If $Q$ is a non-singular matrix of order $3 \times 3$, then which of the following statements is(are) TRUE?

A

$F = PEP$ and $P ^{2}=\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$

B

$\left| EQ + PFQ ^{-1}\right|=| EQ |+\left| PFQ ^{-1}\right|$

C

$\left|( EF )^{3}\right|>| EF |^{2}$

D

Sum of the diagonal entries of $P^{-1} E P+F$ is equal to the sum of diagonal entries of $E+P^{-1} F P$

Solution

Let $A =\begin{bmatrix} C _{1} & C _{2} & C _{3}\end{bmatrix}, B =\begin{bmatrix} R _{1} \\ R _{2} \\ R _{3}\end{bmatrix}$
$AP =\begin{bmatrix} C _{1} & C _{3} & C _{2}\end{bmatrix}$ and $ PB =\begin{bmatrix} R _{1} \\ R _{3} \\ R _{2}\end{bmatrix}$
and $P ^{2}= I$
$P ( EP )= P \begin{bmatrix}1 & 3 & 2 \\ 2 & 4 & 3 \\ 8 & 18 & 13\end{bmatrix}=\begin{bmatrix}1 & 3 & 2 \\ 8 & 18 & 13 \\ 2 & 4 & 3\end{bmatrix}= F$
$| E |=\begin{bmatrix}1 & 2 & 3 \\ 2 & 3 & 4 \\ 8 & 13 & 18\end{bmatrix}\left( R _{3} \rightarrow R _{3}-3 R _{2}-2 R _{1}\right)=\begin{bmatrix}1 & 2 & 3 \\ 2 & 3 & 4 \\ 0 & 0 & 0\end{bmatrix}=0$
$\Rightarrow | F |=0$
$\left| EQ + PFQ ^{-1}\right|=\left| EQ + PPEPQ ^{-1}\right|=\left| EQ + EPQ ^{-1}\right|=| E |\left| Q + PQ ^{-1}\right|=0$
$| EQ |=| E || Q |=0,\left| PFQ ^{-1}\right|=| P || F |\left| Q ^{-1}\right|=0$
(D) $P ^{-1} EP + F = PEP + F =2 F \left(\right.$ as $\left.P ^{-1}= P \right)$
$E + P ^{-1} FP = E + P ^{-1} PEPP =2 E ($ trace $( E )=$ trace $( F ))$

Q12. Let $f: R \rightarrow R$ be defined by $f(x)=\frac{x^{2}-3 x-6}{x^{2}+2 x+4}$. Then which of the following statements is(are) TRUE?

A

$f$ is decreasing in the interval $(-2,-1)$

B

$f$ is increasing in the interval $(1,2)$

C

$f$ is onto

D

Range of $f$ is $\left[-\frac{3}{2}, 2\right]$

Solution

image
$f^{\prime}(x)=\frac{5 x(x+4)}{\left(x^{2}+2 x+4\right)^{2}}$
$f(0)=-\frac{3}{2}$ (point of local minima)
$f(-4)=\frac{11}{6}$ (point of local maxima)

Q13. Let $E , F$ and $G$ be three events having probabilities
$P(E)=\frac{1}{8}, P(F)=\frac{1}{6}$ and $P(G)=\frac{1}{4}$, and let $P(E \cap F \cap G)=\frac{1}{10}$.
For any event $H$, if $H ^{ C }$ denotes its complement, then which of the following statements is(are) TRUE?

A

$P\left(E \cap F \cap G^{C}\right) \leq \frac{1}{40}$

B

$P\left(E^{C} \cap F \cap G\right) \leq \frac{1}{15}$

C

$P(E \cup F \cup G) \leq \frac{13}{24}$

D

$P\left(E^{C} \cap F^{C} \cap G^{C}\right) \leq \frac{5}{12}$

Solution

$P(E)=\frac{1}{8}, P(F)=\frac{1}{6}, P(G)=\frac{1}{4}, P(E \cap F \cap G)=\frac{1}{10}$
(A) $P\left(E \cap F \cap G^{C}\right)=P(E \cap F)-P(E \cap F \cap G)$
$\leq P ( E )- P ( E \cap F \cap G )$
$\leq \frac{1}{8}-\frac{1}{10}$
$\leq \frac{5-4}{40} $
$\leq \frac{1}{40}$
(B) $P\left(E^{C} \cap F \cap G\right)=P(F \cap G)-P(E \cap F \cap G)$
$\leq P(F)-P(E \cap F \cap G)$
$\leq \frac{1}{6}-\frac{1}{10}$
$\leq \frac{10-6}{60}$
$\leq \frac{4}{60}$
$\leq \frac{1}{15}$
(C) $P ( E \cup F \cup G ) \leq P ( E )+ P ( E )+ P ( G )$
$\leq \frac{1}{8}+\frac{1}{6}+\frac{1}{4} $
$\leq \frac{13}{24}$
(D) $P\left(E^{C} \cap F^{C} \cap G^{C}\right)=1-P(E \cup F \cup G)$
$\geq 1-\frac{13}{24}$
$\geq \frac{11}{24}>\frac{10}{24}>\frac{5}{12}$

Q14. For any $3 \times 3$ matrix $M$, let $|M|$ denote the determinant of $M$. Let $I$ be the $3 \times 3$ identity matrix. Let $E$ and $F$ be two $3 \times 3$ matrices such that $( I - EF )$ is invertible. If $G =( I - EF )^{-1}$, then which of the following statements is(are) TRUE?

A

$| FE |=| I - FE || FGE |$

B

$( I - FE )( I + FGE )= I$

C

$EFG = GEF$

D

$( I - FE )( I - FGE )= I$

Solution

$G ( I - EF )=( I - EF ) G = I$
$\Rightarrow G - GEF = G - EFG = I$ ... (1)
(A) $| FE |=| I - FE || FGE |=| FGE - FE FGE |$
$=| FGE - F ( G - I ) E |=| FGE - FGE + FE |=| FE |$
(B) $( I - FE )( I + FGE )= I + FGE - FE - FEFGH$
$= I + FGE - FE - F ( G - I ) E = I + FGE - FE - FGE + FE = I$
(C) From (I) it is true
(D) $( I - FE )( I - FGE )= I - FGE - FE + FEFGE$
$= I - FGE - FE + F ( G - I ) E = I - FGE - FE + FGE - FE$ $= I -2 FE$

Q15. For any positive integer $n$, let $S_{n}:(0, \infty) \rightarrow R$ be defined by
$S_{n}(x)=\displaystyle\sum_{k=1}^{n} \cot ^{-1}\left(\frac{1+k(k+1) x^{2}}{x}\right),$
where for any $x \in R, \cot ^{-1}(x) \in(0, \pi)$ and $\tan ^{-1}(x) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$. Then which of the following statements is(are) TRUE?

A

$S _{10}( x )=\frac{\pi}{2}-\tan ^{-1}\left(\frac{1+11 x ^{2}}{10 x }\right)$, for all $x >0$

B

$\displaystyle\lim _{n \rightarrow \infty} \cot \left(S_{n}(x)\right)=x$, for all $x>0$

C

The equation $S _{3}( x )=\frac{\pi}{4}$ has a root in $(0, \infty)$

D

$\tan \left(S_{n}(x)\right) \leq \frac{1}{2}$, for all $n \geq 1$ and $x>0$

Solution

$S_{n}=\displaystyle\sum_{k=1}^{n} \cot ^{-1}\left\{\frac{1+k(k+1) x^{2}}{x}\right\} $;
$ \displaystyle\sum_{k=1}^{n} \cot ^{-1}\left\{\frac{k(k+1) x^{2}+1}{(k+1) x-k x}\right\}$
$S_{n}=\displaystyle\sum_{k=1}^{n} \cot ^{-1}(k x)-\cot ^{-1}(k+1) x$
$t_{1}=\cot ^{-1}(x)-\cot ^{-1}(2 x)$
$t_{2}=\cot ^{-1}(2 x)-\cot ^{-1}(3 x)$
$t_{3}=\cot ^{-1}(3 x)-\cot ^{-1}(4 x)$
:
$t_{n}=\cot ^{-1}(n x)-\cot ^{-1}((n+1) x)$
$S_{n}=\cot ^{-1}(x)-\cot ^{-1}((n+1) x)$
$\Rightarrow S_{n}=\cot ^{-1}\left(\frac{(n+1) x^{2}+1}{n x}\right)$
$S_{10}=\cot ^{-1}\left(\frac{11 x^{2}+1}{10 x}\right)=\frac{\pi}{2}-\tan ^{-1}\left(\frac{11 x^{2}+1}{10 x}\right)$
(B) $\displaystyle\lim _{n \rightarrow \infty} \cot \left(S_{n}(x)\right)=\displaystyle\lim _{n \rightarrow \infty} \cot \left(\cot ^{-1}\left(\frac{(n+1) x^{2}+1}{n x}\right)\right)$
$=\displaystyle\lim _{n \rightarrow \infty} \frac{n x^{2}+x^{2}+1}{n x}=x$
(C) $S_{3}(x)=\cot ^{-1}\left(\frac{4 x^{2}+1}{3 x}\right)=\frac{\pi}{4} \Rightarrow \frac{1+4 x^{2}}{3 x}=1$
$\Rightarrow 4 x^{2}-3 x+1=0$ have imaginary roots
(D) $\tan \left(S_{n}(x)\right)=\tan \left(\cot ^{-1}\left(\frac{1+(n+1) x^{2}}{n x}\right)\right)$
$=\frac{n x}{1+(n+1) x^{2}}=\frac{1}{\frac{1}{n x}+\frac{(n+1) x}{n}}$

Q16. For any complex number $w=c+$ id, let $\arg (w) \in(-\pi, \pi]$, where $i=\sqrt{-1}$. Let $\alpha$ and $\beta$ be real numbers such that for all complex numbers $z=x+$ iy satisfying $\arg \left(\frac{z+\alpha}{z+\beta}\right)=\frac{\pi}{4}$, then ordered pair $(x, y)$ lies on the circle $x^{2}+y^{2}+5 x-3 y+4=0$. Then which of the following statements is(are) TRUE?

A

$\alpha=-1$

B

$\alpha \beta=4$

C

$\alpha \beta=-4$

D

$\beta=4$

Solution

image
$w=c+i d, \arg (w) \in(-\pi, \pi]$
$\arg \left(\frac{z+\alpha}{z+\beta}\right)=\frac{\pi}{4} ; z_{0}=-\frac{5}{2}+\frac{3}{2} i$
$z_{0}+\alpha=\left(z_{0}+\beta\right) i ; z_{0}+\alpha=z_{0} i+\beta i ; z_{0}(1-i)=\beta i-\alpha $ (by Rotation)
$-\frac{5}{2}+\frac{3}{2} i+\alpha=\left(-\frac{5}{2}+\frac{3}{2} i\right) i+\beta i$
$-\frac{5}{2}+\frac{3}{2} i+\alpha=-\frac{5}{2} i-\frac{3}{2}+\beta i$
$-\frac{5}{2}+\frac{3}{2}+\frac{3}{2} i+\frac{5}{2} i+\alpha=\beta i ;-1+4 i=\beta i-\alpha($ As $\alpha, \beta$ are real number $)$
$\Rightarrow -\alpha=-1, \alpha=1 ; \beta=4$

Q17. For $x \in R$, the number of real roots of the equation $3 x^{2}-4\left|x^{2}-1\right|+x-1=0$ is ______.

Answer: 4

Solution

image
$3 x^{2}-4\left|x^{2}-1\right|+x-1=0$
Case-I: $|x| \geq 1 $
$3 x^{2}-4 x^{2}+4+x-1=0$
$-x^{2}+x+3=0$
$x^{2}-x-3=0 $
$x=\frac{1 \pm \sqrt{1+12}}{2}=\frac{1 \pm \sqrt{13}}{2}=\frac{1+\sqrt{13}}{2}, \frac{1-\sqrt{13}}{2} $
$|x| < 1 $
$3 x^{2}+4 x^{2}-4+x-1=0 $
$7 x^{2}+x-5=0$
$x=\frac{-1 \pm \sqrt{1+20 \times 7}}{14}=\frac{-1 \pm \sqrt{141}}{14}$
So, number of real roots $=4$

Q18. In a triangle $ABC$, let $AB =\sqrt{23}, BC =3$ and $CA =4$. Then the value of $\frac{\cot A +\cot C }{\cot B }$ is ______.

Answer: 2

Solution

image
$A B=\sqrt{23}=C$
$B C=3=a$
$C A=4=b$
$\frac{\cot A+\cot C}{\cot B} ; \frac{\frac{\cos A}{\sin A}+\frac{\cos C}{\sin C}}{\frac{\cos B}{\sin B}}$
$=\frac{\cos A \sin C+\cos C \sin A}{\sin A \cdot \sin C \cdot \frac{\cos B}{\sin B}}=\frac{\sin (A+C) \cdot \sin B}{\sin A \cdot \sin C \cdot \cos B}$
$=\frac{\sin B \cdot \sin B}{\sin A \cdot \sin C \cdot \cos B}$
$=\frac{b^{2}}{a c \cdot \frac{\left(a^{2}+c^{2}-b^{2}\right)}{2 a c}}=\frac{2 b^{2}}{a^{2}+c^{2}-b^{2}}$
$=\frac{2 \times 16}{9+23-16}=\frac{2 \times 16}{32-16}$
$=\frac{2 \times 16}{16}=2$

Q19. Let $\vec{u}, \vec{v}$ and $\vec{w}$ be vectors in three-dimensional space, where $\vec{u}$ and $\vec{v}$ are unit vectors which are not perpendicular to each other and $\vec{ u } \cdot \vec{ w }=1, \vec{ v } \cdot \vec{ w }=1, \vec{ w } \cdot \vec{ w }=4$.
If the volume of the parallelepiped, whose adjacent sides are represented by the vectors $\vec{ u }, \vec{ v }$ and $\vec{ w }$ is $\sqrt{2}$ , then the value of $|3 \vec{u}+5 \vec{v}|$ is ______.

Answer: 7

Solution

$[\vec{ u } \,\,\vec{ v }\,\, \vec{ w }]^{2}=\begin{vmatrix}\vec{ u } \cdot \vec{ u } & \vec{ u } \cdot \vec{ v } & \vec{ u } \cdot \vec{ w } \\ \vec{ u } \cdot \vec{ v } \cdot \vec{ v } & \vec{ v } \cdot \vec{ v } & \vec{ w } \cdot \vec{ w }\end{vmatrix}$
$=\begin{vmatrix}1 & \vec{ u } \cdot \vec{ v } & 1 \\ \vec{ u } \cdot \vec{ u } & 1 & 1 \\ 1 & 4\end{vmatrix}=2$
$=1(3)-\vec{ u } \cdot \vec{ v }(4 \vec{ u } \cdot \vec{ v }-1)+1(\vec{ u } \cdot \vec{ v }-1)=2$
$=3-4(\vec{ u } \cdot \vec{ v })^{2}+\vec{ u } \cdot \vec{ v }+\vec{ u } \cdot \vec{ v }-1=2$
$=-4(\vec{ u } \cdot \vec{ v })^{2}+2 \vec{ u } \cdot \vec{ v }=0$
$(\vec{ u } \cdot \vec{ v })(2-4(\vec{ u } \cdot \vec{ v }))=0 ; \vec{ u } \cdot \vec{ v }=0$,
$ \vec{ u } \cdot \vec{ v }=\frac{1}{2}$
$|3 \vec{ u }+5 \vec{ v }|^{2}=9|\vec{ u }|^{2}+30 \vec{ u } \cdot \vec{ v }+25|\vec{ v }|^{2}$
$=9+15+25=49$
$\therefore |3 \vec{ u }+5 \vec{ v }|=7$