NEET 2022 Physics Questions with Answers Key Solutions

Solution:

$X _{ CM }=\frac{20 \times 10}{20+10}=\frac{20}{3} m$

Solution:

(a) Radio wave (ii) $\approx 10^{2} m$ (ii)
(b) Microwave $\approx$ (iii) $10^{-2} m$ (iii)
(c) Infrared radiations $\approx( iv ) 10^{-4} m$ (iv)
(d) X-ray (i) $\approx \,\mathring{A}=10^{-10} m$ (i)
(a) - (ii), (b) - (iii), (c) - (iv), (d) - (i)

Solution:

$E=P \times t=100 \times 10^{3} \times 3600$
$=36 \times 10^{7} J$

Solution:

$1 :$ Isochoric
$ 2 :$ Adiabatic
$ 3 :$ Isothermal
$4 :$ Isobaric

Solution:

Plane angle and solid angle are dimensionless but have units.

Solution:

In half wave rectification
$ f _{ in}= f _{ out } $
$\Rightarrow f _{\text {out }}=60 \,Hz$

Solution:

$hv = W +\frac{ v _{0}}{2} e$
$\frac{ h v}{2}= W + v _{0} e$
on solving we get, $W =3 / 2 h v$
$h _{ o }=3 / 2 hv$
$v _{0}=3 / 2 v$

Solution:

Velocity is slope of $x-t$ graph
$V =\frac{ dx }{ dt }=\tan \theta $
$\frac{ V _{1}}{ V _{2}}=\frac{\tan \theta_{1}}{\tan \theta_{2}}$
$=\frac{\tan 30^{\circ}}{\tan 45^{\circ}}=\frac{1}{\sqrt{3}}$

Solution:

$\left[ MLT ^{-2} A ^{-2}\right]=$ Magnetic permeability

Solution:

Peak voltage is $\sqrt{2}$ times rms voltages in ac.

Solution:

$S _{ nth }= u +\frac{ a }{2}(2 n -1)$
$=0+\frac{ a }{2}(2 n -1)$
$S _{ nth } \propto(2 n -1)$
$\Rightarrow S _{1 st }, S _{2 nd }, S _{3 rd }, S _{4 th }$
$=[2(1)-1]:[2(2)-1]:[2(3)-1]:[2(4)-1]$
$=1: 3: 5: 7$

Solution:

$I_{g}=\frac{F}{m}$
$=\frac{3}{60 \times 10^{-3}}=50 \,N / kg$

Solution:

${ }_{11}^{22} Na \longrightarrow X +e^{+}+v$
This is $\beta^{+}-$decay
${ }_{11}^{22} Na \longrightarrow{ }_{10}^{22} Ne + e ^{+}+ v$

Solution:

$P = P _{0}+\frac{4 T }{ R }$
$\Rightarrow R$ increases and $P$ decreases

Solution:

As both resistors are in parallel combination so potential drop $( V )$ across both are same.
$ P =\frac{ V ^{2}}{ R } \Rightarrow P \propto \frac{1}{ R } $
$\frac{ P _{1}}{ P _{2}}=\frac{ R _{2}}{ R _{1}}=\frac{200}{100}=\frac{2}{1} $
$=2: 1$

Solution:

$V =\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{ Q }{ R } $
$\frac{1}{4 \pi \epsilon_{0}}=$ constant
$ Q =$ same (Given)
$\therefore V \propto \frac{1}{ R }$
$\therefore$ Potential is more on smaller sphere.

Solution:

$\omega =\omega_{0}+\alpha t $
$ \alpha =\frac{\omega-\omega_{0}}{ t } $
$=\frac{(3120-1200)}{16 s } rpm $
$=\frac{1920}{16} \times \frac{2 \pi}{60} rad / s ^{2}$
$=4 \pi rad / s ^{2} $

Solution:

$n=\sqrt{\epsilon_{ r } u_{r}}$
$n=\frac{c}{v} \Rightarrow v=\frac{c}{n}$
$v=\left(\frac{c}{\sqrt{\epsilon_{r} \mu_{r}}}\right)$

Solution:

$B =\mu_{0} ni =\mu_{0} \frac{ N }{\ell} i$
$\therefore B =4 \pi \times 10^{-7} \times \frac{100}{10^{-3}} \times 1$
$=12.56 \times 10^{-2} T$

Solution:

By conservation of momentum :
$m(0)=\frac{2 m}{5}(-v \hat{i})+\frac{2 m}{5}(-v \hat{j})+\frac{m}{5} \vec{v}^{\prime} $
$\Rightarrow \vec{v}^{\prime}=2 v \hat{i}+2 v \hat{j} $
$\Rightarrow v^{\prime}=\sqrt{(2 v)^{2}+(2 v)^{2}} $
$=2 \sqrt{2} v$

Solution:

For conductors $\alpha$ is (+)ve
For semiconductors & Insulators $\alpha$ is (-)ve

Solution:

$R _{1}= R _{2}=20\, cm =0.2\, m$
$\mu=\frac{3}{2}$
$P =\frac{1}{ f }=(\mu-1)\left(\frac{1}{ R _{1}}-\frac{1}{ R _{2}}\right)$

$P =\left(\frac{3}{2}-1\right)\left(\frac{1}{0.2}+\frac{1}{0.2}\right)$
$P =\frac{1}{2}\left(\frac{2}{0.2}\right)=\frac{10}{2}=+5 D$

Solution:

$dB =\frac{\mu_{0}( Id \vec{\ell} \times \vec{r})}{4 \pi r ^{3}}$
As per Biot Savart law, the expression for magnetic field depends on current carrying element $Id \vec{\ell}$, which is a vector quantity, therefore, statement-I is correct and statement-II is wrong.

Solution:

$B=0.5 T$
Angle between $\vec{B}\, \& \,\vec{A}$ is zero
$\phi =$ B.A. $ \cos 0 $
$=0.5 \times(1) \times 1 $
$=0.5 \,Wb$

Solution:

Constant velocity $\Rightarrow a =0$
$\Rightarrow T = W + f $
$=20000+3000$
$=23000 \,N$

$ \Rightarrow $ Power $= Tv $
$=23000 \times 1.5 $
$=34500 $ watts

Solution:

Method (i)
By Snell's law
$1 \sin 60^{\circ}=\sqrt{3} \sin r $
$\frac{\sqrt{3}}{2}=\sqrt{3} \sin r $
$\sin r=\frac{1}{2} $
$r=30^{\circ}$
Angle between refracted and reflected ray is $90^{\circ}$
Method (ii)
Because angle of incidence is Brewster's angle so that angle between reflected and refracted ray is $90^{\circ}$
$\tan i_{p}=\mu=\sqrt{3}$
$i_{p}=60^{\circ}= i$

Solution:

Radius of wire $=\frac{10^{-2}}{\sqrt{\pi}}$
Cross sectional area $A=\pi r ^{2}=10^{-4} m ^{2}$
$j =\frac{ i }{ A }=\left(\frac{ V }{ R }\right) \cdot \frac{1}{ A }=\frac{ E \ell}{ RA } R =\frac{\rho \ell}{ A }$
$j =\frac{10 \times 10}{10 \times 10^{-4}}=10^{5} A / m ^{2}$
or
$ J =\sigma E \Rightarrow \frac{E}{\rho}=\frac{ E \ell}{ RA }=\frac{10 \times 10 \times \pi}{10 \times 10^{-4} \times \pi} $
$\Rightarrow 10^{5} A / m ^{2}$

Solution:

In (a) & (c) circuits, both the junctions are in same biasing conditions so offers equal resistances.
Since both are in series, therefore equal potential will drop across the junction.

Solution:

$v \propto \sqrt{\text { Tension }}$
$\frac{ v _{ i }}{ v _{ f }}=\sqrt{\frac{ T _{ i }}{ T _{ f }}}$
$\frac{ v _{ i }}{ v _{ f }}=\sqrt{\frac{ T }{2 T }}$
$\frac{ v _{ i }}{ v _{ f }}=\sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}$

Solution:

$k =\sqrt{\frac{ I }{ m }}$
$\Rightarrow \frac{ k _{1}}{ k _{2}}=\sqrt{\frac{ I _{1}}{ I _{2}}}$
$=\sqrt{\frac{ mR ^{2} / 2}{ mR ^{2} / 4}}=\sqrt{2}: 1$

Solution:

$y=(n \lambda)\left(\frac{D}{d}\right)$
$n _{1} \lambda_{1}= n _{2} \lambda_{2}$
$(8) (600 \,nm )= n _{2}(400)$
$n _{2}=12$

Solution:

Electric field is always perpendicular to EPS.

Solution:

Initially speed is zero, then increases & after some time it becomes constant.
Acceleration (slope of $v/t$ curve) of ball first decreases and after some time it becomes zero.

Solution:

First excited state $\Rightarrow n =2$
$T _{1}=-13.6 \frac{ z ^{2}}{ n ^{2}}=-\frac{13.6}{4} eV$
Second excited state $\Rightarrow n =3$
$ T _{2}=-13.6 \frac{ z ^{2}}{ n ^{2}}=-\frac{13.6}{9} eV $
$ T _{1}: T _{2}=\frac{1}{4}: \frac{1}{9}=9: 4$

Solution:

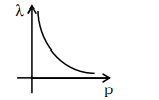
$\lambda=\frac{ h }{ p }$
Graph will be hyperbolic

Solution:

$( n ) T _{\ell}=( n +1) T _{ s }$
$( n ) 2 \pi \sqrt{\frac{1.21}{ g }}=( n +1) 2 \pi \sqrt{\frac{1}{ g }}$
$( n )(1.1)=( n +1)$
$0.1( n )=1$
$n =10$
No. of oscillation of smaller one
$= n +1$
$=10+1$
$=11$

Solution:

$V =$ (no. of moles) $(22.4$ litre)
$=\frac{\text { mass }}{\text { molar mass }}\left(22.4 \times 10^{-3} m ^{3}\right.$ )
$=\frac{4.5 \times 10^{3}}{18} \times 22.4 \times 10^{-3} m ^{3}$
$=5.6 \,m ^{3}$

Solution:

Nuclear Radius :
$R = R _{0}( A )^{1 / 3} $
$\frac{ R (125)}{ R (64)}=\frac{ R _{0}(125)^{1 / 3}}{ R _{0}(64)^{1 / 3}}=\frac{5}{4}$

Solution:

In stretching of a spring shape charges therefore shear modulus is used.
$Y _{\text {copper }}< Y _{\text {steel }}$

Solution:

We have the initial energy as $\frac{1}{2} CV ^2=\frac{1}{2} \times 9 \times 10^{-10} \times 100^2=4.5 \times 10^{-6} J$
Now the capacitor is disconnected and is connected to another $900 pF$ capacitor.
In the steady situation, the two capacitors have their positive plates at the same potential.
Let the common potential difference be $V$ '. The charge on each capacitor is $Q ^{\prime}= CV$ '.
By charge conservation, $Q^{\prime}=Q / 2$. This implies $V^{\prime}=V / 2$.
The total energy of the system is $=2 \times(1 / 2) Q ^{\prime} V '=(1 / 4) QV =2.25 \times 10^{-6} J$
Thus we get the electrostatic energy stored by the system as $\frac{1}{2}\left(C_1+C_2\right) V^2=$ $\frac{1}{2}\left(2 \times 9 \times 10^{-10}\right) \times 50^2=2.25 \times 10^{-6}$

Solution:

Solution:

Area $=$ Length $\times $ Breadth
$=55.3 \times 25 $
$=1382.5$
$=14 \times 10^{2}$
Resultant should have $2$ significant figures.

Solution:

$C=\overline{A \cdot B} \cdot \overline{\bar{A}} \cdot B$
using De-Morgan Theorem
$C=\overline{ A \cdot B +\overline{ A } \cdot B } $
$ C =\overline{ B ( A +\overline{ A })}=\overline{ B }$
Therefore

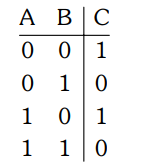
Solution:

$\mu=\frac{ C }{ u } \Rightarrow u \propto \frac{1}{\mu}$
Critical angle
$\operatorname{Sini}_{ c }=\frac{\mu_{ R }}{\mu_{ D }}=\frac{ u _{ D }}{ u _{ R }}=\frac{1.5}{2}=\frac{3}{4} $
$ i _{ c }=\sin ^{-1}\left(\frac{3}{4}\right)$
$\sin \dot{i}_{ c }=\frac{\mu_{ R }}{\mu_{ D }}=\frac{ u _{ D }}{ u _{ R }}$
$i _{ c }=\sin ^{-1}\left(\frac{3}{4}\right)$

Solution:

$i _{\max }=\frac{ E _{\max }}{ R }=\frac{ NBA \omega }{ R }$
$i _{\max }=\frac{1000 \times 2 \times 10^{-5} \times \pi\left(10^{2}\right) \times 2}{12.56}$
$i _{\max }=1 A$

Solution:

Resistance of $P \& Q$ should be approx. equal as it decreases error in experiment.

Solution:

It is electric dipole at large distance electric field intensity
$E=\frac{K P}{R^{3}} \sqrt{1+3 \cos ^{2} \theta} $
$\therefore E \propto \frac{1}{R^{3}}$

Solution:

Gravitational constant $=\left[ M ^{-1} L ^{3} T ^{-2}\right]$
Gravitational potential energy $=\left[ ML ^{2} T ^{-2}\right]$
Gravitational potential $=\left[ L ^{2} T ^{-2}\right]$
Gravitational intensity $=\left[ LT ^{-2}\right]$

Solution:

$\omega=100$
$v=\frac{\omega}{2 \pi}=\frac{100}{2 \pi}=\frac{50}{\pi} Hz$
Resonance frequency
$v_{0}=\frac{1}{2 \pi \sqrt{ LC }}=\frac{1}{2 \pi} \sqrt{\frac{1}{10 \times 10 \times 10^{-6}}} $
$=\frac{50}{\pi} Hz$

Solution:

At highest point only horizontal component of velocity remains
$\Rightarrow u_{x}=u \cos \theta$

$ u _{ x }= u \cos \theta =10 \cos 30^{\circ} $
$=5 \sqrt{3} \,ms ^{-1}$