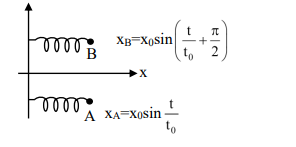JEE Advanced Question Paper with Solution JEE Advanced 2022 Paper 1

Solution

Given $R _{ A }= R _{ B }= R$
$M _{ B }=2 M _{ A }$
Calculation of escape velocity for $A$:
Radius of remaining star $=\frac{ R _{ A }}{2}$.
Mass of remaining star $=\rho_{ A } \frac{4}{3} \pi \frac{ R _{ A }^3}{8}=\frac{ M _{ A }}{8}$
$\frac{- GM _{ A B B }}{ R _{ A / 2}}+\frac{1}{2} mv _{ A }^2=0$
$ \Rightarrow v _{ A }=\sqrt{\frac{2 GM _{ A / B }}{ R _{ A / 2}}}=\sqrt{\frac{ GM _{ A }}{2 R }}$
Calculation of escape velocity for $B$
Mass collected over $B =\frac{7}{8} M _{ A }$
Let the radius of B becomes $r$.
$ \therefore \frac{4}{3} \pi\left( r ^3- R _{ B }^3\right) \rho_{ A }=\frac{7}{8} \rho_{ A } \frac{4}{3} \pi R _{ A }^3 $
$\Rightarrow \pi^3=\frac{7}{8} R _{ A }^3+ R _{ B }^3=\frac{(15)^{1 / 3} R }{2} $
$ \therefore \frac{ V _{ B }^2}{2}=\frac{23 GM _{ A }}{8 \times 15^{1 / 3} \frac{ R }{2}}=\frac{23 GM _{ A }}{4 \times 15^{1 / 3} R } $
$ \therefore V _{ B }=\sqrt{\frac{23 GM _{ A }}{2 \times 15^{1 / 3} R }} $
$ \therefore \frac{ V _{ B }}{ V _{ A }}=\sqrt{\frac{23}{15^{1 / 3}}}=\sqrt{\frac{10 \times 2.30}{15^{1 / 3}}} $
$ n =2.30$

Solution

${ }_7^{16} N +{ }_2^4 He \rightarrow{ }_1^1 He +{ }_8^{19} O $
$ { }_7^{16} N +{ }_2^4 He \rightarrow{ }_1^1 He +{ }_8^{19} O $
$ 16.006 \,\,\,\, 4.003 \,\,\,\, 1.008 \,\,\,\, 19.003 $
$ \left.4 v _0=1 v _1+19 v _2=20 v _2 \,\,\,\,\text { (For max loss of } KE \right) $
$ v _0=\frac{ v _2}{5} $
$ E \text { required }=(1.008+19.003-16.006-4.003) \times 930=1.86 $
$ \frac{1}{2} 4 v _0^2-\frac{1}{2} 20 v ^2=1.86$
$ \frac{1}{2} 4 v _0^2-10 \frac{ v _0^2}{25} 20 v ^2=1.86 $
$ 2 v _0^2-\frac{2}{5} v _0^2=1.86 $
$ \frac{8}{5} v _0^2=1.86 $
$ v _0^2=\frac{1.86 \times 5}{8} $
$ KE =\frac{1}{2} 4 v _0^2=2 v _0^2=\frac{18.6 \times 5}{4}$
$ =2.325$

Solution

Potential difference across the terminals of $C _3$ is $2 V$.
$\therefore Q _3= CV =(4 \mu)(2)=8 \mu C$

Solution

$\frac{ h _{ i }}{ h _0}=\frac{ v }{ u } \Rightarrow \frac{-\frac{30 \sqrt{3}}{13}}{\sqrt{3}}=\frac{ v }{-\frac{43}{3}} \Rightarrow v _1=\frac{430}{13} cm$
$ * \frac{1}{ v }-\frac{1}{ u }=\frac{1}{ f } \Rightarrow \frac{1}{ v }=\frac{1}{10}-\frac{3}{40} \Rightarrow v =40 cm $
$ * x =40-\frac{430}{13}=\frac{90}{13} cm$
$ \tan \alpha=\frac{\frac{30 \sqrt{3}}{13}}{\frac{90}{13}}=\frac{1}{\sqrt{3}} $
$\Rightarrow \alpha=30^{\circ}=\frac{\pi}{6}$
$N =6$

Solution

At $t =0, \omega=0$
at $t =\sqrt{\pi}, \omega=\alpha t =\frac{2}{3} \sqrt{\pi}, $
$v =\omega r =\frac{2}{3} \sqrt{\pi}$
$\theta=\frac{1}{2} \alpha t ^2$
$\theta=\frac{1}{2} \times \frac{2}{3} \times \pi=\frac{\pi}{3}$
$\theta=60^{\circ}$

$ v _{ y }= v \sin 60=\frac{\sqrt{3}}{2} V$
$ h =\frac{ u _{ y }^2}{2 g }=\frac{\frac{3}{4} v ^2}{2 g } $
$ h =\frac{\frac{3}{4} \times \frac{4}{9} \pi}{2 g } $
$h =\frac{3 \pi}{9 \times 2 g }=\frac{\pi}{6 g }$
Maximum height from plane, $H =\frac{ R }{2}+ h$
$ H =\frac{1}{2}+\frac{\pi}{6 \times 10}$
$ x =\frac{\pi}{6} ; x =0.52$

Solution

$ 5+1-1- f =1 a $
$ 5- f = a $
$ \text { About } COM $
$ f 1-2(1(0.5))=\frac{2}{5} Mr ^2 \alpha $
$ \Rightarrow f -1=\frac{2}{5} a$
$ \Rightarrow f =1+\frac{2}{5} a$
$ 5- a =1+\frac{2}{5} a $
$ \Rightarrow 4=\frac{7 a }{5} $
$\Rightarrow a =\frac{20}{7}=2.86\, m / s ^2$

Solution

Maximum energy will be
$ \frac{ q _0^2}{2 C }=\frac{1}{2} LI _0^2$
$ \frac{ q _0^2}{ CL }= I _0^2 $
$ I _0=\frac{ q _0}{\sqrt{ LC }}$
$ I _0=\frac{ CV }{\sqrt{ LC }} $
$ I _0=\sqrt{\frac{ C }{ L }} \times V $
$ V = emf =\left|\frac{ AdB }{ dt }\right|$
$I_0=\sqrt{\frac{10^{-3}}{0.1}} \times 0.04 $
$ V=(1 \times 0.04)$
Maximum current $I _0=0.004=4 \,mA$

Solution

$H _{\max }=\frac{ v ^2 \sin ^2 \theta}{2 g } ; \frac{1}{2} g _{ eff } t ^2= H _{\max }$
$ \Rightarrow t ^2=\frac{2 H _{\max }}{ g _{ eff }} ; t =\sqrt{\frac{ v ^2 \sin ^2 \theta \times 0.81}{ g ^2}} ; t =\frac{0.9 v \sin \theta}{ g }$
$t ^2 =\frac{2 \times v ^2 \sin ^2 \theta}{2 g \left(\frac{ g }{0.81}\right)} $
$d ^{\prime} =\text { New range }=\frac{ d }{2}+ d _1 $
$d _1 = v \cos \theta^{\circ} t $
$ =\frac{ v ^2 \sin ^2 \theta \cos \theta \times 0.9}{ g } ; d ^{\prime}=\frac{ v ^2 \sin 2 \theta}{2 g }+\frac{ v ^2 \sin 2 \theta \times 0.9}{2 g } $
$=\frac{ v ^2 \sin 2 \theta}{ g }\left(\frac{1.0}{2}\right)=0.95 d $
$ n =0.95$

A

The electric field inside the dielectric material is reduced by a factor of $2 K$.

B

The capacitance is decreased by a factor of $\frac{1}{K+1}$.

C

The voltage between the capacitor plates is increased by a factor of $(K+1)$.

D

The work done in the process DOES NOT depend on the presence of the dielectric material.

Solution

For figure (a)

$ C ^{\prime}=\frac{\varepsilon_0 A }{2 d - d + d / k } ; $
$ C ^{\prime}=\frac{ K \varepsilon_0 A }{( K +1) d } ; C ^{\prime}=\frac{ C }{ K +1}$

A

The magnitude of current flowing through $R_1$ is $7.2\, A$.

B

The magnitude of current flowing through $R_2$ is $1.2\, A$.

C

The magnitude of current flowing through $R_3$ is $4.8\, A$.

D

The magnitude of current flowing through $R_5$ is $2.4 \,A$.

Solution

From KCL
$ i _1+ i _2+ i _3=0$
$ \Rightarrow \frac{18- V _0}{3 / 2}+\frac{12- V _0}{1 / 2}+\frac{0- V _0}{3 / 2}=0 $
$ \Rightarrow 18- V _0+36-3 V _0- V _0=0$
$ \Rightarrow 54=5 V _0 $
$ \frac{2\left(\frac{54}{5}- v ^{\prime}\right)}{1}+\frac{18- v ^{\prime}}{1}=0 $
$ \Rightarrow \frac{108}{5}+18=3 V ^{\prime}$
$ \Rightarrow v ^{\prime}=\frac{198}{5 \times 3}=\frac{66}{5} V$
$ I _{ R _1}=\frac{36}{5}=7.2 A $
$ I _{ R _2}=\frac{6}{5}=1.2 A$
$ I _{ R _3}=\frac{24}{5}=4.8 A $
$ I _{ R _5}=\frac{12}{5}=2.4 A $

A

The pressure of the gas at the upper end of the chimney is $300\, Pa$.

B

The velocity of the gas at the lower end of the chimney is $40 \,ms ^{-1}$ and at the upper end is $20\, ms ^{-1}$.

C

The height of the chimney is $590 \,m$.

D

The density of the gas at the upper end is $0.05\, kg\, m ^{-3}$.

Solution

$ \frac{ dm }{ dt }=\rho_1 A _1 v _1=0.8 \,kg / s A $
$ v _1=\frac{0.8}{0.2 \times 0.1}=40 \,m / s $
$ g =10 \,m / s ^2 $
$ \gamma=2$
Gas undergoes adiabatic expansion,
$ p^{1-\gamma} T^\gamma=\text { Constant } $
$ \frac{P_2}{P_1}=\left(\frac{T_1}{T_2}\right)^{\frac{ r }{1-\gamma}} $
$ P_2=\left(\frac{300}{150}\right)^{\frac{2}{-1}} \times 600$
$ P_2=\frac{600}{4}=150 \,Pa$
Now $\rho=\frac{ PM }{ RT } \Rightarrow \rho \propto \frac{ P }{ T }$
$\frac{\rho_1}{\rho_2}=\left(\frac{P_1}{P_2}\right)\left(\frac{T_1}{T_2}\right)=\left(\frac{150}{600}\right)\left(\frac{300}{150}\right)=\frac{1}{2}$
$\rho_2=\frac{\rho_1}{2}=0.1 \,kg / m ^3$
Now $\rho_2 A _2 v _2=0.8 \Rightarrow v _2=\frac{0.8}{0.1 \times 0.4}=20\, m / s$
Now $W _{\text {on gas }}=\Delta K +\Delta U +($ Internal energy $)$
$P _1 A _1 \Delta x _1- P _2 A _2 \Delta x _2=\frac{1}{2} \Delta mV _2^2-\frac{1}{2} \Delta mV V _1^2+\Delta mgh +\frac{ f }{2}\left( P _2 \Delta V _2- P _1 \Delta V _1\right)$
$\Rightarrow 2 P _1 \frac{\Delta V _1}{\Delta m }-2 P _2 \frac{\Delta V _2}{\Delta m }=\frac{ V _2^2- V _1^2}{2}+ gh$
$\Rightarrow \frac{2 \times 600}{0.2}-\frac{2 \times 150}{0.1}=\frac{20^2-40^2}{2}+10 h$
$h =360\, m$

A

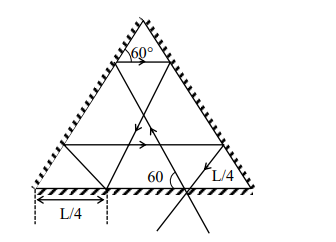
The ray of light will come out for $\theta=30^{\circ}$, for $0< l< L$.

B

There is an angle for $l=\frac{L}{2}$ at which the ray of light will come out after two reflections.

C

The ray of light will NEVER come out for $\theta=60^{\circ}$, and $l=\frac{L}{3}$.

D

The ray of light will come out for $\theta=60^{\circ}$, and $0< l< \frac{L}{2}$ after six reflections.

Solution

(A) Ray will come out after one reflection for $\theta=30^{\circ} \& 0< \ell< L$


for $\theta=60^{\circ} \& \ell=\frac{ L }{2}$, ray will come out after two reflections.
(C) For $\ell=\frac{L}{3} \& \theta=60^{\circ}$ ray will come out after five reflections.

(D) For $\theta=60^{\circ} \& 0< \ell< \frac{L}{2}$, ray will come out after five reflections

A

When $x=q$, the magnitude of the electric field at $O$ is zero.

B

When $x=-q$, the magnitude of the electric field at $O$ is $\frac{q}{6 \pi \in_0 a^2}$.

C

When $x=2 q$, the potential at $O$ is $\frac{7 q}{4 \sqrt{3} \pi \in_0 a}$.

D

When $x=-3 q$, the potential at $O$ is $\frac{3 q}{4 \sqrt{3} \pi \epsilon_0 a}$.

Solution

(A) Due to symmetry $\overrightarrow{ E }_0=0$

$ E _{\text {net }}=\frac{ kq }{(2 d )^2} \times 2=\frac{2 q \times 4}{4 \pi \varepsilon_0 \cdot 4 \cdot 3 a ^2} $
$=\frac{ q }{6 \pi \varepsilon_0 a ^2}$
(C) $v =\frac{7 kq }{2 d }=\frac{7 q }{4 \pi \varepsilon_0 \cdot \sqrt{3} a }=\frac{7 q }{4 \sqrt{3} \pi \varepsilon_0 q }$
(D) $v =\frac{2 kq }{2 d }=\frac{2 q }{4 \pi \varepsilon_0 \cdot \sqrt{3} a }=\frac{ q }{2 \sqrt{3} \pi \varepsilon_0 q }$

A

$E_b^p-E_b^n$ is proportional to $Z(Z-1)$ where $Z$ is the atomic number of the nucleus.

B

$E_b^p-E_b^n$ is proportional to $A^{-\frac{1}{3}}$ where $A$ is the mass number of the nucleus.

C

$E_b^p-E_b^n$ is positive.

D

$E_b^p$ increases if the nucleus undergoes a beta decay emitting a positron.

Solution

Binding energy of proton \& neutron due to nuclear force is same. So difference in binding energy is only due to electrostatic P.E. and it is positive
$E _0^{ P }- E _0^{ n }=\text { electrostatic P.E. }$
$= Z \times P . E$. of one proton
$=Z \times \frac{1}{4 \pi \varepsilon_0} \frac{(Z-1) e ^2}{ R }$
Where $R = R _0 A ^{1 / 3}$
$=\frac{1}{4 \pi \varepsilon_0} \frac{Z(Z-1) e ^2}{ R _0 A ^{\frac{1}{3}}}$

A

$I \rightarrow Q , II \rightarrow P , III \rightarrow S , IV \rightarrow T$

B

$I \rightarrow S , II \rightarrow T, III \rightarrow Q, IV \rightarrow P$

C

$I \rightarrow Q , II \rightarrow P , III \rightarrow S , IV \rightarrow R$

D

$I \rightarrow T , II \rightarrow Q , III \rightarrow P , IV \rightarrow R$

Solution

(I) $\overrightarrow{ B }=\frac{\mu_0 mI }{\sqrt{2}}(\sin \omega t \hat{ j }+\cos \omega t \hat{ k }) $
$ \phi=\overrightarrow{ B } \cdot \overrightarrow{ A }=\frac{\mu_0 mI }{\sqrt{2}} \cos (\omega t ) \cdot A $
$ \varepsilon=\frac{ d \phi}{ dt }=\frac{\mu_0 mI \omega A }{\sqrt{2}} \sin (\omega t ) $
$ i =\frac{\varepsilon}{ R }=\frac{\mu_0 mI \omega A }{\sqrt{2} R } \sin (\omega t )$
$ \overrightarrow{ M }= i \overrightarrow{ A }= iA (\hat{ k })=\frac{\mu_0 mI \omega A ^2}{\sqrt{2} R } \sin (\omega t )(\hat{ k }) $
$\vec{\tau}=\overrightarrow{ M } \times \overrightarrow{ B }=\frac{\mu_0 m ^2 I ^2 \omega A ^2}{\sqrt{2} R } \sin ^2(\omega t )(-\hat{ i }) $
$ =-\left(\frac{\alpha}{4}\right) \hat{ i }$
(II) $ \overrightarrow{ B }=\frac{\mu_0 mI }{\sqrt{2}}(\sin \omega t \hat{ i }+\cos \omega t \hat{ j }) $
$ \phi=0, \varepsilon=0, i =0, t =0$
(III) $ \overrightarrow{ B }=\frac{\mu_0 mI }{\sqrt{2}}(\sin \omega t \hat{ i }+\cos \omega t \hat{ k }) $
$ \phi=\overrightarrow{ B } \cdot \overrightarrow{ A }=\frac{\mu_0 mI }{\sqrt{2}} \cdot \cos (\omega t ) \cdot A $
$ \varepsilon=-\frac{ d \phi}{ dt }=\frac{\mu_0 mI \omega A }{\sqrt{2}} \sin (\omega t )$
$ i =\frac{\varepsilon}{ R }=\frac{\mu_0 mI \omega A }{\sqrt{2} R } \sin (\omega t ) $
$ \overrightarrow{ M }= i \overrightarrow{ A }= iA (\hat{ k })=\frac{\mu_0 mI \omega A ^2}{\sqrt{2} R } \sin (\omega t )(\hat{ k })$
$\vec{\tau}=\overrightarrow{ M } \times \overrightarrow{ B }=\frac{\mu_0 m ^2 I ^2 \omega A ^2}{2 R } \sin ^2(\omega t )(+\hat{ j })$
$ =\frac{\alpha}{4} \hat{ j }$
(IV) $ \overrightarrow{ B }=\frac{\mu_0 mI }{\sqrt{2}}(\cos \omega t \hat{ j }+\sin \omega t \hat{ k }) $
$ \phi=\overrightarrow{ B } \cdot \overrightarrow{ A }=\frac{\mu_0 mI }{\sqrt{2}} \cdot \sin (\omega t ) \cdot A $
$\varepsilon=-\frac{ d \phi}{ dt }=\frac{\mu_0 mI \omega A }{\sqrt{2}} \cos (\omega t ) $
$ i =\frac{\varepsilon}{ R }=-\frac{\mu_0 mI \omega A }{\sqrt{2} R } \cos (\omega t ) $
$ \overrightarrow{ M }= i \overrightarrow{ A }= iA (\hat{ k })=-\frac{\mu_0 mI ^2 A ^2}{\sqrt{2} R } \cos (\omega t )(\hat{ k }) $
$ \vec{\tau}=\overrightarrow{ M } \times \overrightarrow{ B }=-\frac{\mu_0 m ^2 I ^2 \omega A ^2}{2 R } \cos ^2(\omega t )(-\hat{ i }) $
$ =\alpha \cdot \cos ^2\left(\frac{\pi}{6}\right) \hat{ i } $
$ =\frac{3 \alpha}{4} \hat{ i }$

A

$I \rightarrow R , II \rightarrow T, III \rightarrow P, IV \rightarrow S$

B

$ I \rightarrow S, II \rightarrow P, III \rightarrow Q, IV \rightarrow R$

C

$ I \rightarrow S, II \rightarrow T, III \rightarrow P, IV \rightarrow R$

D

$I \rightarrow T, II \rightarrow P, III \rightarrow R, IV \rightarrow S$

Solution

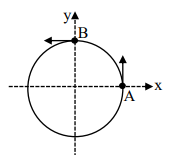
(I) $v_{B A}^2=v_A^2+v_B^2-2 v_{A B} \cos \theta$
As $\omega_{ A }=\omega_{ B }, \theta=90^{\circ}$ remains constant.
Also, $v _{ A }= v _{ B }=1 \,m / s$
So, $v _{ BA }=\sqrt{2} m / s$
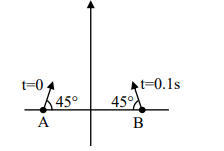
(II) $\overrightarrow{ u }_{ A }=\frac{5 \pi}{2} \hat{ i }+\frac{5 \pi}{2} \hat{ j }$
$\overrightarrow{ v }_{ A }=\frac{5 \pi}{2} \hat{ i }+\left(\frac{5 \pi}{2}-10 \cdot \frac{\pi}{3}\right) \hat{ j }$
$=\frac{5 \pi}{2} \hat{ i }-\frac{5 \pi}{6} \hat{ j }$
$\overrightarrow{ u }_{ B }=-\frac{5 \pi}{2} \hat{ i }+\frac{5 \pi}{2} \hat{ j }$
$ \overrightarrow{ u }_{ B }=-\frac{5 \pi}{2} \hat{ i }-\left(\frac{5 \pi}{6}+1\right) \hat{ j }$
$ \overrightarrow{ v }_{ B , A }=-5 \pi \hat{ i }-\hat{ j } $
$ v _{ BA }=\sqrt{25 \pi^2+1}$
(III) $x _{ A }=\sin t$
$ v _{ A }=\cos t =\frac{1}{2} m / s $
$ x _{ B }=\operatorname{cost} $
$ v _{ B }=-\sin t =-\frac{\sqrt{3}}{2} m / s$
$ v _{ BA }=-\frac{\sqrt{3}}{2}-\frac{1}{2}$
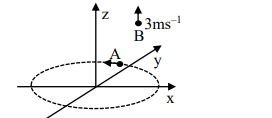
(IV) $\vec{v}_{ A }\, \&\, \vec{v}_{\underline{B}}$ are always perpendicular
So, $\left|\overrightarrow{ v }_{ BA }\right|=\sqrt{ v _{ A }^2+ v _{ B }^2}=\sqrt{10}\, m / s$

A

I $\rightarrow$ T, II $\rightarrow$ R, III $\rightarrow$ S, IV $\rightarrow$ Q

B

I $\rightarrow$ S, II $\rightarrow$ P, III $\rightarrow$ T, IV $\rightarrow$ P

C

I $\rightarrow$ P, II $\rightarrow$ R, III $\rightarrow$ T, IV $\rightarrow$ Q

D

I $\rightarrow$ Q, II $\rightarrow$ R, III $\rightarrow$ S, IV $\rightarrow$ T

Solution

(I) $ \Delta U =\Delta Q -\Delta W$
$=\left\{\left(10^{-3} \times 2250\right)-\frac{10^5\left(10^{-3}-10^{-6}\right)}{10^3}\right\} kJ $
$ =(2.25-0.0999) kJ$
$=(2.1501) \,kJ $
(II) $ \Delta U = nC _{ V } \Delta T $
$ =\frac{5}{2} nR \Delta T$
$ =\frac{5}{2} \cdot(0.2)(8)(1500-500) J $
$ =4 \,kJ $
(III) $ P_1 V_2^\gamma=P_2 V_2^\gamma $
$ \Rightarrow 2\left(\frac{1}{3}\right)^{5 / 3}=P_2\left(\frac{1}{24}\right)^{5 / 3} $
$\Rightarrow P_2=64 \, k \,Pa$
$ \Delta U=n_{ v } \Delta T =\frac{3}{2} \cdot\left( P _2 V _2- P _1 V _1\right) $
$ =\frac{3}{2}\left(64 \times \frac{1}{24}-2 \times \frac{1}{3}\right) kJ $
$ =3 \, kJ $
(IV) $ \Delta U = nC _{ V } \Delta T$
$ = n \cdot \frac{7}{2} R \Delta T$
$ =\frac{7}{9} \Delta Q $
$ =7 \, kJ$

A

$I \rightarrow$ P, II $\rightarrow$ R, III $\rightarrow$ Q, IV $\rightarrow$ T

B

I $\rightarrow$ Q, II $\rightarrow$ P, III $\rightarrow$ T, IV $\rightarrow$ S

C

I $\rightarrow$ P, II $\rightarrow$ T, III $\rightarrow$ R, IV $\rightarrow$ Q

D

$I \rightarrow T$, II $\rightarrow$ S, III $\rightarrow$ Q, IV $\rightarrow$ R

Solution

(I) $v _1=\frac{ uf }{ u + f } $
$=\frac{(-20)(10)}{(-20)+(10)}=+20$
$ u _2=+15 $
$ v _2= \frac{(15)(15)}{(15)+(15)}=+7.5$
(II)$ v _1=+20 $
$ u _2=+15$
$v _2=\frac{(15)(-10)}{(15)+(-10)}=-30$
(III) $v _1=+20$
$u _2=+15$
$v_2=\frac{(15)(-20)}{(15)+(-20)}=60$
(IV) $ v _1=\frac{(-20)(-20)}{(-20)+(-20)}=-10 $
$ u _2=-15 $
$ v _2=\frac{(-15)(10)}{(-15)+(10)}=30$

Solution

$ Q _{ rxn }= C \Delta T $
$ |\Delta U | \times 2=20 \times 14.8 $
$|\Delta U |=148 \,kJ / mol $
$ \Delta U =-148\, kJ / mol $
$ Hg ( g )+\frac{1}{2} O _2( g ) \longrightarrow HgO ( s ): \Delta U =-148 \,kJ / mol $
$ \Delta H =\Delta U +\Delta n _{ g } RT$
$ =-148-\frac{3}{2} \times \frac{8.3}{1000} \times 298=-151.7101 $
$ Hg (l)+\frac{1}{2} O _2( g ) \longrightarrow HgO ( s ) $
$ \Delta H =-151.7101+61.32=-90.39\, kJ / mol $

Solution

For the required reaction $\Delta G ^{\circ}=\Delta G ^{\circ}+\Delta G _2^{\circ}+\Delta G ^{\circ}$
$ \Rightarrow 7 \times E =1.68 \times 3+1.21 \times 2+(-1.03) \times 2$
$ E =\frac{5.4}{7}=0.7714$

Solution

Final mixture has 20 milli moles $NaHCO _3$ and 10 milli moles $Na _2 CO _3$
$ pH = pKa _2+\log \frac{\text { Salt }}{\text { Acid }} $
$ pH = pKa _2+\log \left(\frac{10}{20}\right) $
[Buffer : $Na _2 CO _3+ NaHCO _3$ ]
$ =10.32-\log 2=10.02$

Solution

$ \underset{0.02}{2 Cu \left( NO _3\right)_2}+5 KI \longrightarrow Cu _2 I _2+ \underset{0.01}{KI _3}+4 KNO _3 $
$ \underset{0.01}{KI _3}+ H _2 S \longrightarrow \underset{0.01}{S \downarrow}+ KI +2 HI $
$ n _{ S }=0.01$ mole
weight of sulphur $=32 \times 0.01=0.32\, gm$

Solution

Mole of $P _4=\frac{1.24}{31 \times 4}=0.01$
$\underset{0.01 \text { mole }}{P _4+3 NaOH} +3 H _2 O \longrightarrow \underset{0.01 \text { mole } }{PH _3}+3 NaH _2 PO _2 $
$\underset{0.01}{2 PH _3}+\underset{\frac{3}{2} \times 0.01}{3 CuSO _4} \rightarrow Cu _3 P _2+3 H _2 SO _4$
$=\frac{0.03}{2} \text { moles } $
$ W _{ CuSO _4}=\frac{0.03}{2} \times 159=2.385\, gm $

Solution

$\operatorname{lg~R} \rightarrow \frac{1}{250}$ moles
No. of Br Atoms $\rightarrow \frac{2}{250}$ moles
Moles of $AgBr \rightarrow \frac{2}{250}$ moles
Mass of $AgBr =\frac{2}{250} \times(108+80)=1.504$

A

$\sigma$ orbital has a total of two nodal planes.

B

$\sigma^*$ orbital has one node in the $x z$-plane containing the molecular axis.

C

$\pi$ orbital has one node in the plane which is perpendicular to the molecular axis and goes through the center of the molecule.

D

$\pi^*$ orbital has one node in the $x y$-plane containing the molecular axis.

Solution

A

Chemisorption results in a unimolecular layer.

B

The enthalpy change during physisorption is in the range of 100 to $140\, kJ\, mol ^{-1}$.

C

Chemisorption is an endothermic process.

D

Lowering the temperature favors physisorption processes.

Solution

(A) Chemisorption is unimolecular layered.
(B) Enthalpy of physisorption is much less in magnitude.
(C) Chemisorption of gases on solids is exothermic.
(D) As physisorption is exothermic so lowering temperature favours it.

A

the reaction of $Al _2 O _3$ with coke (C) at a temperature $>2500^{\circ} C$.

B

the neutralization of aluminate solution by passing $CO _2$ gas to precipitate hydrated alumina $\left( Al _2 O _3 .3 H _2 O \right)$

C

the dissolution of $Al _2 O _3$ in hot aqueous $NaOH$.

D

the electrolysis of $Al _2 O _3$ mixed with $Na _3 AlF _6$ to give $Al$ and $CO _2$.

Solution

(A) Electrochemical extraction of Aluminum from bauxite done below $2500^{\circ} C$
(B) $2 Na \left[ Al ( OH )_4\right]_{ aq .}+2 CO _{2( g )} \rightarrow Al _2 O _3 .3 H _2 O _{\text {(s) }} \downarrow+2 NaHCO _{3( aq .)}$
The sodium aluminate present in solution is neutralised by passing $CO _2$ gas and hydrated $Al _2 O _3$ is precipitated.
(C) $Al _2 O _{3( s )}+2 NaOH _{\text {(aq.) }}+3 H _2 O _{(l)} \rightarrow 2 Na \left[ Al ( OH )_4\right]_{\text {aq. }}$
Concentration of bauxite is carried out by heating the powdered ore with hot concentrated solution of $NaOH$
(D) In metallurgy of aluminum, $Al _2 O _3$ is mixed with $Na _3 AlF _6$

A

paramagnetic

B

bent in geometry

C

an acidic oxide

D

colorless

Solution

$ 3 PbS +8 HNO _3 \rightarrow 3 Pb \left( NO _3\right)_2+2 NO +4 H _2 O + S $
$NO \Rightarrow$ Neutral oxide, Paramagnetic, Linear geometry, Colourless gas

A

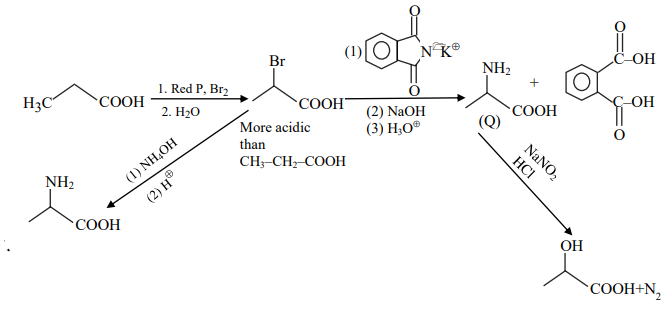
$P$ can be reduced to a primary alcohol using $NaBH _4$.

B

Treating $P$ with conc. $NH _4 OH$ solution followed by acidification gives $Q$.

C

Treating $Q$ with a solution of $NaNO _2$ in aq. $HCl$ liberates $N _2$.

D

$P$ is more acidic than $CH _3 CH _2 COOH$.

A

B

C

D

A

I $\rightarrow$ P; II $\rightarrow$ Q; III $\rightarrow$ S; IV $\rightarrow$ T

B

$I \rightarrow R$; II $\rightarrow$ S; III $\rightarrow$ S; IV $\rightarrow$ T

C

I $\rightarrow$ P; II $\rightarrow$ Q; III $\rightarrow$ Q; IV $\rightarrow$ R

D

$I \rightarrow R$; II $\rightarrow S$; III $\rightarrow$ Q; IV $\rightarrow R$

Solution

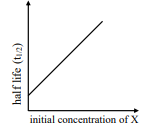
(I)$\text { rate }=\frac{ k [ x ]}{ x _{ s }+[ x ]}=\frac{ k }{\frac{ x _{ s }}{[ x ]}+1}$
$ \text { If }[ x ] \rightarrow \infty \Rightarrow \text { rate } \rightarrow k \Rightarrow \text { order }=0 $
$ \Rightarrow ( I )-( R ),( P )$
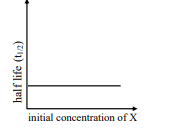
(II)$ {[ x ]< < x _{ s } \Rightarrow \text { rate }=\frac{ k [ x ]}{ x _{ s }} \Rightarrow \text { order }=1} $
$ \Rightarrow \text { (II) }-( Q ), \text { (T) }$
(III) $[ x ]>> x _{ s } \Rightarrow$ rate $= k \Rightarrow$ order $=0$
$\Rightarrow ( III )-( P ),( S )$
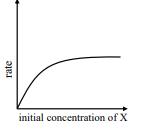
(IV)$ \text { rate }=\frac{ k [ x ]^2}{ x _{ s }+[ x ]} $
$ {[ x ]>> x _{ s } \Rightarrow \text { rate }= k [ x ] } $
$ \Rightarrow( IV )-( Q ),( T )$

A

$I \rightarrow Q$; II $\rightarrow$ P; III $\rightarrow$ S; IV $\rightarrow$ R

B

I $\rightarrow$ T; II $\rightarrow$ P; III $\rightarrow$ Q; IV $\rightarrow$ R

C

I $\rightarrow$ T; II $\rightarrow$ R; III $\rightarrow$ Q; IV $\rightarrow$ P

D

I $\rightarrow$ Q; II $\rightarrow$ R; III $\rightarrow$ S; IV $\rightarrow$ P

Solution

(P) $Mg \left( HCO _3\right)_2+2 Ca ( OH )_2 \rightarrow Mg ( OH )_2+2 CaCO _3+2 H _2 O$
(Q) $BaO _2+ H _2 SO _4 \rightarrow H _2 O _2+ BaSO _4$
(R) $Ca ( OH )_2+ MgCl _2 \rightarrow Mg ( OH )_2+ CaCl _2$
(S) $BaO _2+2 HCl \rightarrow BaCl _2+ H _2 O _2$
(T) $Ca \left( HCO _3\right)_2+ Ca ( OH )_2 \rightarrow 2 CaCO _3+2 H _2 O$

A

I $\rightarrow$ R, T; II $\rightarrow$ P, S; III $\rightarrow$ Q, T; IV $\rightarrow$ P , Q

B

I $\rightarrow$ R, S; II $\rightarrow$ P , T; III $\rightarrow$ P, Q; IV $\rightarrow$ Q, T

C

I $\rightarrow$ P, R; II $\rightarrow$ R, S; III $\rightarrow$ R, T; IV $\rightarrow$ P, T

D

I $\rightarrow$ Q, T; II $\rightarrow$ S, T; III $\rightarrow$ P, T; IV $\rightarrow$ Q, R

Solution

(1) $\left[ Cr ( CN )_6\right]^{4-}$
$Cr ^{+2}=[ Ar ]_{18} 3 d ^4 4 s ^0 ;$ low spin complex

$P , R , T$
(2) $\left[ RuCl _6\right]^{2-}$
$Ru ^{+4}=[ Kr ]_{36} 4 d ^4 5 s ^0$; low spin complex

$P , R , S , T$
(3) $\left[ Cr \left( H _2 O \right)_6\right]^{2+}$
$Cr ^{+2}=[ Ar ]_{18} 3 d ^4 4 s ^0$; high spin complex

$ Q,T $
(4) $\left[ Fe \left( H _2 O \right)_6\right]^{2+}$
$Fe ^{+2}=[ Ar ]_{18} 3 d ^6 ;$ High spin complex

$P, Q$

A

I $\rightarrow$ P, Q; II $\rightarrow$ S; III $\rightarrow$ Q, R; IV $\rightarrow$ P

B

I $\rightarrow$ P ; II $\rightarrow$ R, S; III $\rightarrow$ R; IV $\rightarrow$ Q, S

C

I $\rightarrow$ Q, S; II $\rightarrow$ P, T; III $\rightarrow$ P; IV $\rightarrow$ S

D

I $\rightarrow$ P, S; II $\rightarrow$ T; III $\rightarrow$ Q, R; IV $\rightarrow$ P

Solution

$ \cos ^{-1} \sqrt{\frac{2}{2+\pi^2}}=\tan ^{-1} \frac{\pi}{\sqrt{2}}$

$ \sin ^{-1}\left(\frac{2 \sqrt{2} \pi}{2+\pi^2}\right)=\sin ^{-1}\left(\frac{2 \times \frac{\pi}{\sqrt{2}}}{1+\left(\frac{\pi}{\sqrt{2}}\right)^2}\right) $
$ =\pi-2 \tan ^{-1}\left(\frac{\pi}{\sqrt{2}}\right)$
$\left(\right.$ As, $\left.\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)=\pi-2 \tan ^{-1} x, x \geq 1\right)$
$ \text { and } \tan ^{-1} \frac{\sqrt{2}}{\pi}=\cot ^{-1}\left(\frac{\pi}{\sqrt{2}}\right)$
$ \therefore \text { Expression }=\frac{3}{2}\left(\tan ^{-1} \frac{\pi}{\sqrt{2}}\right)+\frac{1}{4}\left(\pi-2 \tan ^{-1} \frac{\pi}{\sqrt{2}}\right)+\cot ^{-1}\left(\frac{\pi}{\sqrt{2}}\right) $
$ =\left(\frac{3}{2}-\frac{2}{4}\right) \tan ^{-1} \frac{\pi}{\sqrt{2}}+\frac{\pi}{4}+\cot ^{-1} \frac{\pi}{\sqrt{2}} $
$=\left(\tan ^{-1} \frac{\pi}{\sqrt{2}}+\cot ^{-1} \frac{\pi}{\sqrt{2}}\right)+\frac{\pi}{4} $
$ =\frac{\pi}{2}+\frac{\pi}{4}=\frac{3 \pi}{4} $
$=2.35 \text { or } 2.36$

Solution

$\displaystyle\lim _{x \rightarrow a^{+}} \frac{2 \ln (\sqrt{x}-\sqrt{\alpha})}{\ln \left( e ^{\sqrt{x}}- e ^{\sqrt{a}}\right)}\left(\frac{0}{0} \text { form }\right)$
$\therefore$ Using Lopital rule,
$ =2 \displaystyle\lim _{x \rightarrow a^{+}} \frac{\left(\frac{1}{\sqrt{x}-\sqrt{\alpha}}\right) \cdot \frac{1}{2 \sqrt{x}}}{\left(\frac{1}{e^{\sqrt{x}}-e^{\sqrt{x}}}\right) \cdot e^{\sqrt{x}} \cdot \frac{1}{2 \sqrt{x}}} $
$ =\frac{2}{e^{\sqrt{x}}}\displaystyle \lim _{x \rightarrow a^{+}} \frac{\left(e^{\sqrt{x}}-e^{\sqrt{x}}\right)}{(\sqrt{x}-\sqrt{\alpha})}\left(\frac{0}{0}\right)$
$ =\frac{2}{e^{\sqrt{x}}} \displaystyle\lim _{x \rightarrow a^{+}} \frac{\left(e^{\sqrt{x}} \cdot \frac{1}{2 \sqrt{x}}-0\right)}{\left(\frac{1}{2 \sqrt{x}}-0\right)}=2$
so, $\displaystyle \lim _{x \rightarrow a^{+}} f(g(x))=\lim _{x \rightarrow a^{+}} f(2)$
$= f (2)=\sin \frac{\pi}{6}=\frac{1}{2} $
$ =0.50$

Solution

$n ( U )=900$
Let $A \equiv$ Fever, $B \equiv$ Cough
$C \equiv$ Breathing problem
$ \therefore n ( A )=190, n ( B )=220, n ( C )=220$
$ n ( A \cup B )=330, n ( B \cup C )=350$
$ n ( A \cup C )=340, n ( A \cap B \cap C )=30$
Now $n(A \cup B)=n(A)+n(B)-n(A \cap B)$
$\Rightarrow 330=190+220-n(A \cap B)$
$\Rightarrow n ( A \cap B )=80$
Similarly,
$ 350=220+220- n ( B \cap C )$
$ \Rightarrow n ( B \cap C )=90$
and $340=190+220-n(A \cap C)$
$ \Rightarrow n ( A \cap C )=70 $
$ \therefore n ( A \cup B \cup C )=(190+220+220)-(80+90+70)+30$
$ =660-240=420 $
$ \Rightarrow$ Number of person without any symptom
$ = n (\cup)- n ( A \cup B \cup C )$
$ =900-420=480$
Now, number of person suffering from exactly one symptom
$ =(n(A)+n(B)+n(C))-2(n(A \cap B)+n(B \cap C)+n(C \cap A))+3 n(A \cap B \cap C) $
$ =(190+220+220)-2(80+90+70)+3(30)$
$ =630-480+90=240$
$ \therefore $ Number of person suffering from atmost one symotom
$ =480+240=720 $
$ \Rightarrow \text { Probability }=\frac{720}{900}=\frac{8}{10}=\frac{4}{5}=0.80$

Solution

Given that
$z \neq \overline{ z }$
Let $\alpha=\frac{2+3 z+4 z^2}{2-3 z+4 z^2}=\frac{\left(2-3 z+4 z^2\right)+6 z}{2-3 z+4 z^2}$
$\therefore \alpha=1+\frac{6 z}{2-3 z+4 z^2}$
If $\alpha$ is a real number, then
$ \alpha=\bar{\alpha} $
$ \Rightarrow \frac{z}{2-3 z+4 z^2}=\frac{\bar{z}}{2-3 \bar{z}+4 \bar{z}^2} $
$ \therefore 2(z-\bar{z})=4 z \bar{z}(z-\bar{z}) $
$\Rightarrow(z-\bar{z})(2-4 z \bar{z})=0$
As $z \neq \overline{ z }$ (Given)
$ \Rightarrow z \bar{z}=\frac{2}{4}=\frac{1}{2}$
$ \Rightarrow|z|^2=0.50$

Solution

$ \overline{ Z }- z ^2=i\left(\overline{ Z }+ z ^2\right) $
$ \Rightarrow(1-i) \overline{ z }=(1+i) z ^2$
$\Rightarrow \frac{(1-i)}{(1+i)} \overline{ z }= z ^2 $
$ \Rightarrow\left(-\frac{2 i}{2}\right) \overline{ z }= z ^2 $
$ \therefore z ^2=-i \overline{ z }$
Let $z = x +i y$,
$\therefore\left( x ^2- y ^2\right)+i(2 xy )=-i( x -i y )$
so, $x ^2- y ^2+ y =0$....(1)
and $(2 y+1) x=0$...(2)
$\Rightarrow x =0 \text { or } y =-\frac{1}{2}$
Case I: When $x =0$
$ \therefore(1) \Rightarrow y(1-y)=0 \Rightarrow y=0,1 $
$ \therefore(0,0),(0,1)$
Case II : When $y =-\frac{1}{2}$
$ \therefore(1) \Rightarrow x^2-\frac{1}{4}-\frac{1}{2}=0 \Rightarrow x^2=\frac{3}{4} \Rightarrow x=\pm \frac{\sqrt{3}}{2}$
$ \therefore\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right),\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$
$\Rightarrow$ Number of distinct ' $z$ ' is equal to 4.

Solution

Given
$A _{51}- A _{50}=1000 \Rightarrow \ell_{51} w _{51}-\ell_{50} w _{50}=1000 $
$ \Rightarrow\left(\ell_1+50 d _1\right)\left( w _1+50 d _2\right)-\left(\ell_1+49 d _1\right)\left( w _1+49 d _2\right)=1000 $
$\Rightarrow\left(\ell_1 d _2+ w _1 d _1\right)=10 $
$\left(\text { As } d _1 d _2=10\right)$
$ \therefore A _{100}- A _{90}=\ell_{100} w _{100}-\ell_{90} w _{90} $
$=\left(\ell_1+99 d _1\right)\left( w _1+99 d _2\right)-\left(\ell_1+89 d _1\right)\left( w _1+89 d _2\right) $
$ =10\left(\ell_1 d _2+ w _1 d _1\right)+\left(99^2-89^2\right) d _1 d _2$
$=10(10)+\underbrace{(99-89)}_{=10}(99+89)(10)$
$\left(\text { As, } d_1 d_2=10\right) $
$=100(1+188)=100(189)$
$ =18900$

Solution

$C _1\left(\frac{1}{2}, \frac{3}{2}\right)$ and $r _1=\frac{\sqrt{10}}{2}$
$C _2=( r , r )$
$\therefore$ circle $C _2$ touches $C _1$ internally
$ \Rightarrow C _1 C _2=\left| r -\frac{\sqrt{10}}{2}\right| $
$ \Rightarrow\left( r -\frac{1}{2}\right)^2+\left( r -\frac{3}{2}\right)^2=\left( r -\frac{\sqrt{10}}{2}\right)^2 $
$r ^2-4 r +\sqrt{10} r =0 $
$ r =0 \text { (reject) or } r =4-\sqrt{10}$

A

No $a$ satisfies the above equation

B

An integer $a$ satisfies the above equation

C

An irrational number $a$ satisfies the above equation

D

More than one $a$ satisfy the above equation

Solution

$\int\limits_1^e \frac{\left(\log _c x\right)^{1 / 2}}{x\left(a-\left(\log _c x\right)^{3 / 2}\right)^2}=1$
Let $a-\left(\log _c x \right)^{3 / 2}= t$
$ \frac{\left(\log _e x\right)^{1 / 2}}{x} d x=-\frac{2}{3} d t $
$ =\frac{2}{3} \int\limits_a^{a-1} \frac{-d t}{t^2}=\frac{2}{3}\left(\frac{1}{t}\right)_a^{a-1}=1 $
$ \frac{2}{3 a(a-1)}=1$
$3 a^2-3 a-2=0 $
$ a=\frac{3 \pm \sqrt{33}}{6}$

A

$T_{20}=1604$

B

$\displaystyle\sum_{ k =1}^{20} T_{ k }=10510$

C

$T_{30}=3454$

D

$\displaystyle\sum_{ k =1}^{30} T_{ k }=35610$

Solution

$ a _1=7, d =8$
$ T _{ n +1}- T _{ n }= a _{ n } \forall n \geq 1$
$ S _{ n }= T _1+ T _2+ T _3+\ldots+ T _{ n -1}+ T _{ n }$
$ S _{ n }= T _1+ T _2+ T _3+\ldots+ T _{ n -1}+ T _{ n }$
on subtraction
$ T _{ n }= T _1+ a _1+ a _2+\ldots+ a _{ n -1}$
$T _{ n }=3+( n -1)(4 n -1) $
$ T _{ n }=4 n ^2-5 n +4$
$ \sum_{ k =1}^{ n } T _{ k }=4 \sum n ^2-5 \sum n +4 n $
$ T _{20}=1504$
$T _{30}=3454$
$ \displaystyle\sum_{ k =1}^{30} T _{ k }=35615$
$ \displaystyle\sum_{ k =1}^{20} T _{ k }=10510$

A

$\frac{x-1}{0}=\frac{y-1}{0}=\frac{z-1}{5}$

B

$\frac{x-6}{-5}=\frac{y}{2}=\frac{z}{3}$

C

$\frac{x}{-2}=\frac{y-4}{5}=\frac{z}{4}$

D

$\frac{x}{1}=\frac{y-4}{-2}=\frac{z}{3}$

Solution

line of intersection is $\frac{x}{0}=\frac{y-4}{-4}=\frac{z}{5}$
(1) Any skew line with the line of intersection of given planes can be edge of tetrahedron.
(2) any intersecting line with line of intersection of given planes must lie either in plane $P_1$ or $P_2$ can be edge of tetrahedron.

A

$3(\alpha+\beta)=-101$

B

$3(\beta+\gamma)=-71$

C

$3(\gamma+\alpha)=-86$

D

$3(\alpha+\beta+\gamma)=-121$

Solution

$ \overrightarrow{ r }=\hat{ k }+ t (-\hat{ i }+\hat{ j })+ p (-\hat{ i }+\hat{ k }) $
$\overrightarrow{ n }=\hat{ i }+\hat{ j }+\hat{ k } $
$\Rightarrow x + y + z =1 $
$Q (10,15,20) \text { and } S (\alpha, \beta, \gamma) $
$ \frac{\alpha-10}{1}=\frac{\beta-15}{1}=\frac{\gamma-20}{1}=-2\left(\frac{10+15+20-1}{1+1+1}\right) $
$ =-\frac{88}{3} $
$ \Rightarrow(\alpha, \beta, \gamma) \equiv\left(-\frac{58}{3},-\frac{43}{3},-\frac{28}{3}\right) $
$ \Rightarrow A , B , C $ are correct options

A

$S Q_l=2$

B

$Q _1 Q _2=\frac{3 \sqrt{10}}{5}$

C

$PQ _1=3$

D

$SQ _2=1$

Solution

Let equation of tangent with slope ' $m$ ' be

$T : y = mx +\frac{1}{ m }$
$T$ : passes through $(-2,1)$ so
$1=-2 m+\frac{1}{m}$
$\Rightarrow m =-1 \text { or } m =\frac{1}{2}$
Points are given by $\left(\frac{ a }{ m ^2}, \frac{2 a }{ m }\right)$
So, one point will be $(1,-2) \&(4,4)$
Let $P_1(4,4) \& P_2(1,-2)$
$ P _1 S : 4 x -3 y -4=0$
$ P _2 S : x -1=0$
$ PQ _1=\left|\frac{4(-2)-3(1)-4}{5}\right|=3 $
$ SP =\sqrt{10} ; PQ _2=3 ; SQ _1=1= SQ _2 $
$ \frac{1}{2}\left(\frac{ Q _1 Q _2}{2}\right) \times \sqrt{10}=\frac{1}{2} \times 3 \times 1 \text { (comparing Areas) }$
$\Rightarrow Q _1 Q _2=\frac{2 \times 3}{\sqrt{10}}=\frac{3 \sqrt{10}}{5}$

A

$p \left(\frac{3+\sqrt{2}}{4}\right)<0$

B

$p \left(\frac{1+3 \sqrt{2}}{4}\right)>0$

C

$p \left(\frac{5 \sqrt{2}-1}{4}\right)>0$

D

$p \left(\frac{5-\sqrt{2}}{4}\right)<0$

Solution

$f(\theta)=\frac{1}{2}\begin{vmatrix} & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1\end{vmatrix}+\begin{vmatrix}\sin \pi & \cos \left(\theta+\frac{\pi}{4}\right) & \tan \left(\theta-\frac{\pi}{4}\right) \\ \sin \left(\theta-\frac{\pi}{4}\right) & -\cos \frac{\pi}{2} & \log _c\left(\frac{4}{\pi}\right) \\ \cot \left(\theta+\frac{\pi}{4}\right) & \log _c \frac{\pi}{4} & \tan \pi\end{vmatrix}$
$f(\theta)=\frac{1}{2}\begin{vmatrix}2 & \sin \theta & 1 \\ 0 & 1 & \sin \theta \\ 0 & -\sin \theta & 1\end{vmatrix}+\begin{vmatrix}0 & -\sin \left(\theta-\frac{\pi}{4}\right) & \tan \left(\theta-\frac{\pi}{4}\right) \\ \sin \left(\theta-\frac{\pi}{4}\right) & 0 & \log _{ c }\left(\frac{4}{\pi}\right) \\ -\tan \left(\theta-\frac{\pi}{4}\right) & -\log _{ c }\left(\frac{4}{\pi}\right) & 0\end{vmatrix}$
$ f (\theta)=\left(1+\sin ^2 \theta\right)+0 \text { (skew symmetric) } $
$ g (\theta)=\sqrt{ f (\theta)-1}+\sqrt{ f \left(\frac{\pi}{2}-\theta\right)-1}$
$=|\sin \theta|+|\cos \theta| \text { for } \theta \in\left[0, \frac{\pi}{2}\right] $
$ g (\theta) \in[1, \sqrt{2}] $
$ \text { Again let } P ( x )= k ( x -\sqrt{2})( x -1) $
$ 2-\sqrt{2}= k (2-\sqrt{2})(2-1) $
$ \Rightarrow k =1 ( P (2)=2-\sqrt{2} \text { given) } $
$ \therefore P ( x )=( x -\sqrt{2})( x -1) $
$\text { for option (A) } P \left(\frac{3+\sqrt{2}}{4}\right)<0 \text { correct }$ $ \text { option (B) } P \left(\frac{1+3 \sqrt{2}}{4}\right)<0 \text { incorrect }$
option (C) $P \left(\frac{5 \sqrt{2}-1}{4}\right) >0$ correct
option (D) $P \left(\frac{5-\sqrt{2}}{4}\right) >0$ incorrect

A

(I) $\rightarrow$ (P); (II) $\rightarrow$ (S); (III) $\rightarrow$ (P); (IV) $\rightarrow$ (S)

B

(I) $\rightarrow$ (P); (II) $\rightarrow$ (P); (III) $\rightarrow$ (T); (IV) $\rightarrow$ (R)

C

(I) $\rightarrow$ (Q); (II) $\rightarrow$ (P); (III) $\rightarrow$ (T); (IV) $\rightarrow$ (S)

D

(I) $\rightarrow$ (Q); (II) $\rightarrow$ (S); (III) $\rightarrow$ (P); (IV) $\rightarrow$ (R)

Solution

(I) $\left\{x \in\left[\frac{-2 \pi}{3}, \frac{2 \pi}{3}\right]: \cos x+\sin x=1\right\}$
$\cos x+\sin x=1$
$\Rightarrow \frac{1}{\sqrt{2}} \cos x +\frac{1}{\sqrt{2}} \sin x =\frac{1}{\sqrt{2}} $
$ \Rightarrow \cos \left( x -\frac{\pi}{4}\right)=\cos \frac{\pi}{4} $
$ \Rightarrow x -\frac{\pi}{4}=2 n \pi \pm \frac{\pi}{4} ; n \in Z $
$ \Rightarrow x =2 n \pi ; x =2 n \pi+\frac{\pi}{2} ; n \in Z $
$ \Rightarrow x \in\left\{0, \frac{\pi}{2}\right\} $ in given range has two solutions
(II) $ \left\{ x \in\left[\frac{-5 \pi}{18}, \frac{5 \pi}{18}\right]: \sqrt{3} \tan 3 x =1\right\} $
$ \sqrt{3} \tan 3 x =1 \Rightarrow \tan 3 x =\frac{1}{\sqrt{3}} \Rightarrow 3 x = n \pi+\frac{\pi}{6} $
$ \Rightarrow x =(6 n +1) \frac{\pi}{18} ; n \in Z $
$ \Rightarrow x \in\left\{\frac{\pi}{18}, \frac{-5 \pi}{18}\right\} $ in given range has two solutions
(III) $\left\{x \in\left[-\frac{6 \pi}{5}, \frac{6 \pi}{5}\right]: 2 \cos (2 x)=\sqrt{3}\right\} $
$ 2 \cos 2 x=\sqrt{3} $
$ \Rightarrow \cos 2 x=\frac{\sqrt{3}}{2}=\cos \frac{\pi}{6}$
$\Rightarrow 2 x =2 n \pi \pm \frac{\pi}{6} ; n \in Z $
$ \Rightarrow x = n \pi \pm \frac{\pi}{12} ; n \in Z $
$ x \in\left\{\pm \frac{\pi}{12}, \pi \pm \frac{\pi}{12},-\pi \pm \frac{\pi}{12}\right\}$
Six solutions in given range
(IV) $ \left\{x \in\left[-\frac{7 \pi}{4}, \frac{7 \pi}{4}\right]: \sin x-\cos x=1\right\} $
$ \cos x-\sin x=-1 $
$ \Rightarrow \cos \left(x+\frac{\pi}{4}\right)=\frac{-1}{\sqrt{2}}=\cos \frac{3 \pi}{4} $
$ \Rightarrow x+\frac{\pi}{4}=2 n \pi \pm \frac{3 \pi}{4} ; n \in Z$
$\Rightarrow x=2 n \pi+\frac{\pi}{2} \text { or } x =2 n \pi-\pi ; n \in Z $
$ \Rightarrow x \in\left\{\frac{\pi}{2}, \frac{-3 \pi}{2}, \pi,-\pi\right\} $ four solutions in given range