JEE Main Physics Question Paper with Solution 2023 February 1st Shift 2 - Evening
A
$\left[h^1 c ^1 G ^{-1}\right]$
B
$\left[h^{-1 / 2} c^{1 / 2} G^{1 / 2}\right]$
C
$\left[h^{1 / 2} c^{1 / 2} G^{-1 / 2}\right]$
D
$\left[h^{1 / 2} c^{-1 / 2} G^1\right]$
Solution
Say dimensional formale of mass is $H ^{ x } C ^{ y } G ^z$
$ M^1=\left(M L^2 T^{-1}\right)^x\left(L^{-1}\right)\left(M^{-1} L^3 T^{-2}\right)^Z$
$M^1 L^0 T^0=M^{x-z} L^{2 x+y+3 z} T^{-x-y z}$
on comparing both side
$ x-z=1 $
$ 2 x+y+3 z=0 $
$ -x-y-2 z=0$
On solving above equations we get
$x =\frac{1}{2} y =\frac{1}{2} z =\frac{-1}{2}$
A
$\frac{(n-1) R}{(2 n-1)}$
B
$\frac{(n-1) R}{n}$
C
$\frac{n^2 R}{n-1}$
D
$\frac{(n-1) R}{n^2}$
Solution

Suppose resistance of each arm is $r$, then $r=R / n$
$R_{e q(A B)}=\frac{R_1 R_2}{R_1+R_2}$
$ \frac{r(n-1) r}{r+(n-1) r}$
$ =\frac{r(n-1) r}{n r}$
$ =\frac{n-1}{n} r $
$ =\frac{( n -1) R}{n^2}$
A
$\frac{3}{2}$
B
$\frac{2}{3}$
C
$\frac{3}{4}$
D
$\frac{4}{3}$
Solution
$V _{ e }=\sqrt{\frac{2 GM }{ R }}=\sqrt{\frac{2 G \rho \frac{4}{3} \pi R ^3}{ R }}= C \sqrt{\rho} \cdot R $
$ \frac{ V _{ e _1}}{ V _{ e _2}}=\frac{ R _1}{ R _2} \sqrt{\frac{\rho_1}{\rho_2}}=\frac{1}{2} $
$ \frac{ R _1^2}{ R _2^2} \times \frac{\rho_1}{\rho_2}=\frac{1}{4}$
$ \frac{ R _1}{ R _2}=\frac{1}{3} $
$ g =\frac{ GM ^2}{ R ^2}=\frac{ G \frac{4}{3} \pi R ^3 \times \rho}{ R ^2} C \cdot \rho R $
$ \frac{ g _1}{ g _2}=\frac{\rho_1 R _1}{\rho_2 R _2}=\frac{1}{4} \frac{ R _2^2}{ R _1^2} \times \frac{ R _1}{ R _2} $
$ =\frac{1}{4} \times \frac{ R _2}{ R _1}=\frac{3}{4}$
A
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
B
Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$
C
A is true but $R$ is false
D
A is false but $R$ is true
Solution
Potential of a conducting sphere is
$V =\frac{ KQ }{ R }$ (Solid as well as hollow)
$V _1= V _2$ and $R _1= R _2$
$\therefore Q _1= Q _2$
A
$\frac{v_1}{v_2}=\frac{1}{8}$
B
$\frac{v_1}{v_2}=\frac{1}{4}$
C
$\frac{v_1}{v_2}=\frac{1}{16}$
D
$\frac{v_1}{v_2}=\frac{1}{2}$
Solution
$ K _{\max }= hf - hf _0 $
$ \text { For } f =2 f _0 $
$ \frac{1}{2} m V _1^2=2 h _0- hf _0= hf _0 $
$ \text { For } f =5 f _0 $
$ \frac{1}{2} m V _2^2=5 hf_{0 } - hf f _0=4 hf f _0$
$ \frac{ V _1}{ V _2}=\frac{1}{2} $
Q6. Figures (a), (b), (c) and (d) show variation of force with time.

The impulse is highest in figure.
A
Fig (b)
B
Fig (c)
C
Fig (a)
D
Fig (d)
Solution
Impulse $=$ Area under $F = t$ curve
(a) $\frac{1}{2} \times 1 \times 0.5=\frac{1}{4} N . s$
(b) $0.5 \times 2=1$ N.s (maximum)
(c) $\frac{1}{2} \times 1 \times 0.75=\frac{3}{8} N . s$
(d) $\frac{1}{2} \times 2 \times 0.5=\frac{1}{2}$ N.s
A
$62\, K$
B
$16.5\, K$
C
$33\, K$
D
$66 \,K$
Solution
$ T _{ H }=99^{\circ} C =99+273 $
$ =372 K$
$ 1-\frac{ T _{ C }}{ T _{ H }}=\frac{1}{3}$
$ \frac{ T _{ C }}{ T _{ H }}=\frac{2}{3} (1) \Rightarrow T _{ C }=\frac{2}{3} \times 372 $
$ =2 \times 124=248 K $
$ 1-\frac{ T _{ C }+ X }{ T _{ H }}=\frac{1}{6}$
$ \frac{5}{6}=\frac{ T _{ C }+ X }{ T _{ H }} $
$ \frac{5}{6}=\frac{248+ X }{372}$
$248+X=5 \times 62 $
$ X =310-248=62 K$
A
A and C only
B
A, B and C only
C
A, B and D only
D
A and B only
Solution
$ \phi=\vec{ B } \cdot \vec{ A }$
$ = BA \cdot \cos \theta$
Most suitable ans is 2 [Otherwise ABCD]
A
$2: 1$
B
$1: 2$
C
$1: 1$
D
$4: 1$
Solution
Modulating Index
$\mu= \frac{A_m}{A_c} $
$\mu_1 =\frac{X}{Y}$
$\mu_2 =\frac{X}{2 Y}$
$\frac{\mu_1}{\mu_2} =\frac{2}{1}$
A
It works as a voltage regulator in reverse bias and behaves like simple pn junction diode in forward bias.
B
It works as a voltage regulator in both forward and reverse bias.
C
It works as a voltage regulator only in forward bias.
D
It works as a voltage regulator in forward bias and behaves like simple pn junction diode in reverse bias.
Solution
Woks as voltage regulator in reverse bias and as simple P-n junction in forward bias.
A
$6\, \mu T$
B
$4 \,\mu T$
C
$3\, \mu T$
D
$1\, \mu T$
Solution
$B _{ C } =\frac{\mu_0 I }{4 \pi R }(\pi)( B \text { at centre of circular arc })$
$=\frac{\mu_0 I }{4 R }=\frac{4 \pi \times 10^{-7} \times 3}{4 \times \frac{\pi}{10}} $
$ =3 \times 10^{-6} T =3 \mu T$
A
$-373^{\circ} C$
B
$-40^{\circ} C$
C
$-100^{\circ} C$
D
$-273^{\circ} C$
Solution
For isochoric process
$\frac{ P }{ T }= n \frac{ R }{ V }=\text { constan } t$
$P =\frac{ nR }{ V }( t +273)$
If $P =0 \Rightarrow t =-273^{\circ} C$
A
2
B
3
C
$\frac{1}{2}$
D
1
Solution
$< u _{ E }>=< u _{ B }>=\frac{1}{2}< u _{\text {total }}>$
So $\frac{\left\langle u _{ E }\right\rangle}{\left\langle u _{\text {total }}\right\rangle}=\frac{1}{2}$
A
$40 \,cm$
B
$160 \,cm$
C
$60 \,cm$
D
$100\, cm$
Solution

by mirror formula
$ \frac{1}{ v }+\frac{1}{ u }=\frac{1}{ f } $
$ \frac{1}{ v _1}+\frac{1}{-15}=\frac{1}{(-20)}$
$\frac{1}{ v _1}=-\frac{1}{20}+\frac{1}{15} $
$ =\frac{-3+4}{60}$
$ v _1=60\, cm $
$\frac{1}{ v _2}+\frac{1}{(-25)}=\frac{1}{(-20)}$
$\frac{1}{ v _2}=\frac{-1}{20}+\frac{1}{25} $
$ =\frac{-5+4}{100}=\frac{-1}{100} $
$ v _2=-100 \,cm $
$ d =60+100=160 \,cm$
A
B
C
D
Solution
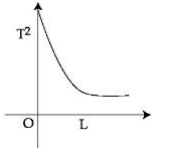
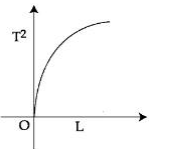
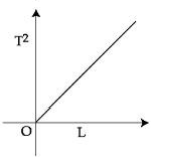
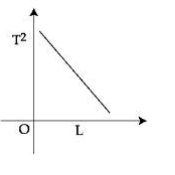
$T =2 \pi \sqrt{\frac{\ell}{ g }} $
$ T ^2 =\frac{4 \pi^2}{ g } \times \ell $
$ T ^2 \alpha \ell$
A
$40.8 \,eV$
B
$3.4 \,eV$
C
$10.5 \,eV$
D
$13.6 \, eV$
Solution
$\Delta E =13.6 Z ^2\left[\frac{1}{2^2}-\frac{1}{4^2}\right] eV $
$ =13.6 \times(4)^2\left(\frac{1}{4}-\frac{1}{16}\right) eV$
$ =13.6[4-1] eV$
$ =13.6 \times 3=40.8\, eV $
A
$20\, N$
B
$35.7\, N$
C
$33.3 \,N$
D
$25.2\, N$
Solution

$ N = Mg - F \operatorname{Sin} 30^{\circ}$
$ = mg -\frac{ F }{2}=100-\frac{ F }{2}=\frac{200- F }{2}$
$F \operatorname{Cos} 30^{\circ}=\mu N$
$ \sqrt{3} \frac{ F }{2}=0.25 \times\left(\frac{200- F }{2}\right)$
$ 4 \sqrt{3} F =200- F $
$ F =\frac{200}{4 \sqrt{3}+1}=25.22$
A
$0.1\,cm$
B
$1 \,mn$
C
$1 \,cm$
D
$0.1 \,mm$
Solution
Tension $(F)=m g$
$ =4 \times \frac{10}{4}=10 N$
$ \Delta L =\frac{ FL }{ AY }$
$=\frac{10 \times 6}{3 \times 10^{-6} \times 2 \times 10^{11}}$
$ =10^{-4} m =0.1\, mm$
Q19. For a body projected at an angle with the horizontal from the ground, choose the correct statement.
A
The Kinetic Energy (K.E.) is zero at the highest point of projectile motion.
B
The horizontal component of velocity is zero at the highest point.
C
The vertical component of momentum is maximum at the highest point.
D
Gravitational potential energy is maximum at the highest point.
Solution
At highest point
$V _{ y }=0$
$ V _{ x }= u _{ x }= u \cos \theta$
$U _{ g }= mgh ,$ it is maximum at $ H _{\max } $
A
Both $A$ and $R$ are correct but $R$ is not the correct explanation of $A$
B
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
C
A is not correct but $R$ is correct
D
A is correct but $R$ is not correct
Solution
Error of voltmeter decreases with increase in its resistance.
Answer: 50
Solution

$ U _{ f }=\frac{1}{2} k \left(\frac{ x _0}{2}\right)^2 $
$ K _{ f }=0.25\, J $
$ \frac{1}{2} kx _0^2+0=\frac{1}{2} k \frac{ x _0^2}{4}+0.25 $
$\frac{1}{2} kx _0^2 \frac{3}{4}=\frac{1}{4} $
$ \frac{1}{2} k \frac{3}{100}=1 \Rightarrow k =\frac{200}{3} N / m $
$ =67 \,N / m $
Answer: 3
Solution

$ I = I _{ cm }+ Md ^2 $
$ =\frac{ MR ^2}{2}+ MR ^2 $
$ =\frac{3}{2} MR ^2 $
$ x =3$
Answer: 288
Solution

$ \vec{ E }= E _0 \times \hat{ i } $
$ \phi_{\text {net }}=\phi_{ ABCD }= E _0 a \cdot a ^2$
$ \frac{ q _{\text {en }}}{\epsilon_0}= E _0 a ^3 $
$ q _{ en }= E _0 \in_0 a ^3 $
$ =4 \times 10^4 \times 9 \times 10^{-12} \times 8 \times 10^{-6} $
$ =288 \times 10^{-14} C $
$ Q =288$
Answer: 2
Solution

$ I_1=I_2=\frac{20-10}{10}=1 A $
$ I_3=1 A $
$ \left|\frac{I_1+I_3}{I_2}\right|=2$
Answer: 2
Solution
$ A _1 V _1= A _2 V _2 $
$ 750 \times 10^{-4} V _1=500 \times 10^{-6} \times 0.3 $
$ V _1=\frac{500 \times 3 \times 10^{-3}}{750} m / s $
$ =2 \times 10^{-3} m / s $
$ \frac{ dh }{ dt }=-2 \times 10^{-3} m / s$
Answer: 4
Solution
Fringe shift $=\frac{t(\mu-1)}{\lambda} B $
$ =\frac{10 \times 10^{-6}(1.2-1)}{5 \times 10^{-7}} B $
$ =\frac{10^{-5} \times 0.2}{5 \times 10^{-7}}=4$
Answer: 6
Solution
For A mass number $=34$
Total binding energy $=1.2 \times 34=40.8\, MeV$
For $B$ mass number $=26$
total binding energy $=1.8 \times 26 \,MeV$
$=46.8\, MeV$
Difference of $BE =6\, MeV$
Answer: 44
Solution
$N =600, A =70 \times 10^{-4} m ^2, B =0.4 T $
$ \omega=\frac{500 \times 2 \pi}{60}=\frac{100 \pi}{6} rad / s $
$ E = NAB \omega \sin \omega t $
$\omega t \text { is angle } b / w \vec{ A } \,\& \,\vec{ B } $
$ =600 \times 70 \times 10^{-4} \times 0.4 \times \frac{100 \pi}{6} \times \frac{1}{2} $
$=44\, V $
Answer: 200
Solution
$u =20 \,m / s , S _1=500\, m , v =0$
By third equation of mation
$ 0=(20)^2-2 a .500 \Rightarrow a =\frac{4}{10} m / s ^2$
$ u =20 \,m / s , S _2=250\, m , v =?$
$ v ^2=(20)^2-2 a .250$
$ = v =\sqrt{200} \,m / s$
$x =200$
Answer: 132
Solution
$ F =5+3 y ^2 $
$ W=\int\limits_2^5\left(5+3 y^2\right) d y $
$=\left[5 y+\frac{3 y^3}{3}\right]_2^5 $
$ =132\, J$
JEE Main Chemistry Question Paper with Solution 2023 February 1st Shift 2 - Evening
A
(A) is not correct but (R) is correct
B
Both $( A )$ and $( R )$ are correct and $( R )$ is the correct explanation of $( A )$
C
Both (A) and (R) are correct but (R) is not the correct explanation of (A)
D
(A) is correct but (R) is not correct
Solution
(Gypsum is used for making fireproof wall boards
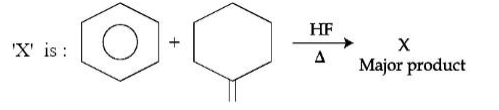
A
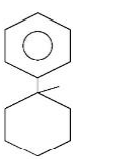
B
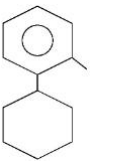
C
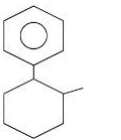
D

A
steel manufacturing
B
manufacturing of cement
C
Industrial production of urea
D
Electricity generation in thermal power plants
Solution
In urea production $NH _3$ and $CO _2$ consumed so least responsible for global warming.
A
2-ethylanthraquinol
B
$BaO _2$
C
$BaO$
D
$K _2 S _2 O _8$
Solution
$\left( K _2 S _2 O _8( s )+2 D _2 O ( l ) \rightarrow 2 KDSO _4\right.$ (aq. $)+ D _2 O _2$
A
addition of helium will not affect the equilibrium.
B
the equilibrium will shift in the forward direction and more of $Cl _2$ and $PCl _3$ gases will be produced.
C
the equilibrium will go backward due to suppression of dissociation of $PCl _5$.
D
helium will deactivate $PCl _5$ and reaction will stop.
Solution
$PCl ( g ) \rightleftharpoons PCl _3( g )+ Cl _2( g )$
(Case 1 : At constant $P$ - volume will increase so reaction will shift in forward direction then answer will be $A$
Case 2 : At constant volume no change in active mass so reaction will not shift in any direction then answer will be D.
A
$N ^{3-}, O ^{2-}, F ^{-}, S ^{2-}$
B
$Li ^{+}, Na ^{+}, Mg { }^{2+}, Ca ^{2+}$
C
$Ba ^{2+}, Sr ^{2+}, K ^{+}, Ca ^{2+}$
D
$K ^{+}, Cl ^{-}, Ca ^{2+}, Sc ^{3+}$

A
$C - C > Si - Si > Ge - Ge > Sn - Sn$
B
$C - C > Si - Si > Sn - Sn > Ge - Ge$
C
$Si - Si > C - C > Ge - Ge > Sn - Sn$
D
$Si - Si > C - C > Sn - Sn > Ge - Ge$
Solution
(Bond enthalpy order
$C - C > Si - Si > Ge - Ge > Sn - Sn)$
A
$\left[ Co \left( H _2 O \right)_6\right]^{3+}$
B
$\left[ Co \left( NH _3\right)_5 Cl \right]^{+}$
C
$\left[ Co \left( NH _3\right)_5 NO _2\right]^{2+}$
D
$\left[ Co \left( NH _3\right)_5 Cl \right]^{2+}$
Solution
$[ Co ( NH _3)_5 NO _2]^{2+}$
Two linkage isomers possible
$NO _2 \rightarrow \text { Ambidentate ligand }$
A
Iodine
B
Oxygen
C
Mercury
D
Potassium
Solution
(Nessler's Reagent $\rightarrow K _2\left[ HgI _4\right]$
A
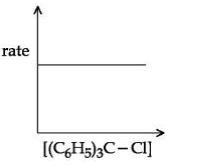
B
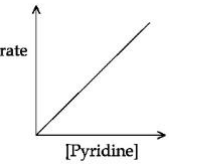
C
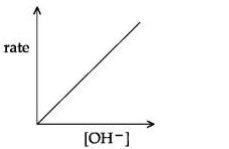
D
Solution
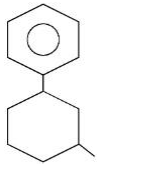
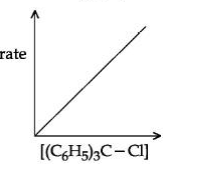
(It is SN1 reaction so rate of reaction depends on the concentration of alkyl halide only
A
Both (A) and (R) are correct and (R) is the correct explanation of (A)
B
(A) is correct but (R) is not correct
C
Both (A) and (R) are correct but (R) is not the correct explanation of $( A )$
D
(A) is not correct but (R) is correct
Solution
$2 Cu ^{+} \rightarrow Cu ^{2+}+ Cu$
The stability of $Cu ^{2+}( aq )$ rather than $Cu ^{+}( aq )$, is due to the much more negative $\Delta_{\text {hyd }} H$ of $Cu ^{2+}$ (aq) than $Cu ^{+}( aq )$, which more than compensates for the second ionisation enthalpy of $Cu$.
A
(A) is correct but (R) is not correct
B
(A) is not correct but (R) is correct
C
Both $( A )$ and $( R )$ are correct but $(R)$ is not the correct explanation of $( A )$
D
Both $( A )$ and $( R )$ are correct and $( R )$ is the correct explanation of $( A )$
Solution
$KOH$ absorb $CO _2$
So its concentration should be checked.
A
$\Delta_{ eg } H ( Cl )<\Delta_{ eg } H ( F )$
B
$\Delta_{ eg } H ( I )<\Delta_{ eg } H ( At )$
C
$\Delta_{ eg } H ( Te )<\Delta_{ eg } H ( Po )$
D
$\Delta_{ eg } H ( Se )<\Delta_{ eg } H ( S )$

A
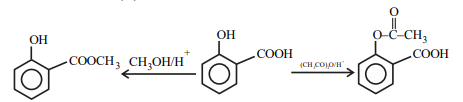
$CH _3 OH / H ^{+}, \Delta$ and $CH _3 OH / H ^{+}, \Delta$
B
$\left( CH _3 CO \right)_2 O / H ^{+}$and $CH _3 OH / H ^{+}, \Delta$
C
$\left( CH _3 CO \right)_2 O / H ^{+}$and $\left( CH _3 CO \right)_2 O / H ^{+}$
D
$CH _3 OH / H ^{+}, \Delta$ and $\left( CH _3 CO \right)_2 O / H ^{+}$
A
Both (A) and (R) are correct and (R) is the correct explanation of (A)
B
(A) is not correct but (R) is correct
C
Both (A) and (R) are correct but (R) is not the correct explanation of (A)
D
$( A )$ is correct but $( R )$ is not correct
A
Both Statement I and Statement II are correct
B
Both Statement I and Statement II are incorrect
C
Statement I is incorrect but Statement II is correct
D
Statement I is correct but Statement II is incorrect
Solution

Does not show esterification test.
Presence of both sulphur and nitrogen give red
colour in Lassigne’s test.
A
$3$ and $2.505$
B
$3$ and $0.7033$
C
$0.3$ and $\log 2.505$
D
$0.3$ and $0.7033$
Solution
$\frac{ x }{ m }= Kp ^{1 / n } $
$ \log \frac{ x }{ m }=\log k +\frac{1}{ n } \log P $
$ \left. Y =3 x +2.505, \frac{1}{ n }=3, \log K =2.505\right)$
A
$X$-longer, $Y$-shorter
B
$X$ - shorter, $Y$ - longer
C
$X$ - shorter, $Y$ - shorter
D
$X$-longer, $Y$-longer
Solution
According to bent rule more electronegative atom occupy less s-characters so bond length increases. $O - H$ bond will be short than $O - F$ bond due to small size of $H$ than $F$
Answer: 3
Solution
(chlorodiazepoxide, Veronal, Valium is tranquilizer where as salvarsan is antibiotic
Answer: 372
Solution
$ i =1+( n -1) \alpha $
$( i =1+0.2(2-1)=1.2 $
$ \Delta T _{ f }= i K _{ f } m $
$ \Delta T _{ f }=1.2 \times 1.86 \times \frac{5 \times 1000}{60 \times 500} $
$\Delta t _{ f }=3.72 $
$ \Delta T _{ f }=372 \times 10^{-2}$
Answer: 139
Solution
( $10\, ml$ solute in $90 \,ml$ solvent
mass of solute $=10 \times 3.2=32 \,g$
mass of solvent $=90 \times 1.6 \,g$
$m =\frac{32 \times 1000}{160 \times 90 \times 1.6}=1.388$
$m-138.8 \times 10^{-2}-139$
Answer: 3
Solution
$FeS$ and $Cu _2 S$, present in copper matte.
Answer: 1006
Solution
(Bomb calorimeter $\rightarrow$ const volume
Heat released
By combustion of 1 mole
$C _2 H _6(\Delta U )=-\frac{20 \times 0.5}{0.3} \times 30=-1000\, kJ $
$C _2 H _6( g )+7 / 2 O _2( g ) \rightarrow 2 CO _2( g )+3 H _2 O (l) $
$ \Delta ng =2-(2+7 / 2)=-(7 / 2)$
$ \Delta H =\Delta U +\Delta nRT$
$=-1000-7 / 2 \times 8.3 \times 300\, k J $
$=-1000-6.225 $
$ =-1006 \,kJ$
So heat released $=1006\, kJ \,mol ^{-1}$
Answer: 14
Solution
$ {\left[ Ag ^{+}\right]=10^{-5}}$
${\left[ NO _3^{-}\right]=10^{-5}} $
$[Br^-]= \frac{Ksp}{[Ag^+]}= 4.9 \times 10^{-8}$
$\Lambda_{ m }=\frac{ k }{1000 \times M } $
For $Ag ^{+}$
$ 6 \times 10^{-3}=\frac{ K _{ Ag ^{+}}}{1000 \times 10^{-5}}$
$ K _{ Ag +}=6 \times 10^{-5} $
$ \Rightarrow 6000 \times 10^{-8} $
$ \text { for } Br ^{-} $
$ 8 \times 10^{-3}=\frac{ K _{ Br ^{-}}}{1000 \times 4.9 \times 10^{-8}}$
$ K _{ Br -}=39.2 \times 10^{-8} $
$ \text { for } NO _3^{-}$
$7 \times 10^{-3} =\frac{ K _{ NO _3^{-}}}{1000 \times 10^{-5}} $
$K _{ NO _3} =7 \times 10^{-5} $
$ =7000 \times 10^{-8}$
Conductivity of solution
$ \Rightarrow(6000+7000+39.2) \times 10^{-8} $
$\Rightarrow 13039.2 \times 10^{-8} S m ^{-1}$
Answer: 4
Solution
$d =\frac{Z \times M}{N_{ A } a ^3} $
$\frac{ d _{ FCC }}{ d _{ BCC }}=\frac{\frac{4 \times M _{ w }}{ N _{ A } \times(2)^3}}{\frac{2 \times M _{ w }}{ N _{ A } \times(2.5)^3}}=3.90$
Answer: 6
Solution
$ \left[ Mn \left( H _2 O \right)_6\right]^{2+}$
$ Mn ^{2+}=3 d ^5 $
$ \mu=\sqrt{5(5+2)}=5.91\, BM $
Answer: 75
Solution
Assume reaction starts with 1 mole $A$
$\left( t _{1 / 2}=\frac{ a }{2 k }, K =\frac{1}{2 \times 50}\right.$
For $75 \%$ completion
$ a -\frac{ a }{4}= kt $
$ t =\frac{3}{4} \frac{ a }{ k }=\frac{3}{4} \times \frac{100}{ a }=75$
JEE Main Mathematics Question Paper with Solution 2023 February 1st Shift 2 - Evening
A
both $R_1$ and $R_2$ are not equivalence relations
B
only $R_2$ is an equivalence relation
C
only $R_1$ is an equivalence relation
D
both $R_1$ and $R_2$ are equivalence relations
Solution
$ S =\{1,2,3, \ldots \ldots 10\} $
$P ( S )=\text { power set of } S $
$ AR , B \Rightarrow( A \cap \vec{ B }) \cup(\vec{ A } \cap B )=\phi $
$ R 1 \text { is reflexive, symmetric } $
$ \text { For transitive } $
$ ( A \cap \vec{ B }) \cup(\vec{ A } \cap B )=\phi ;\{ a \}=\phi=\{ b \} A = B $
$ ( B \cap \vec{ C }) \cup(\vec{ B } \cap C )=\phi \therefore B = C $
$ \therefore A = C \text { equivalence. }$

$ R _2 \equiv A \cup \vec{ B }=\vec{ A } \cup B$
$ R _2 \rightarrow $ Reflexive, symmetric for transitive

$ A \cup \vec{ B }=\vec{ A } \cup B \Rightarrow\{ a , c , d \}=\{ b , c , d \} $
$ \{ a \}=\{ b \}$
$ \therefore A = B $
$ B \cup \vec{ C }=\vec{ B } \cup C \Rightarrow B = C$
$\therefore A = C $
$\therefore A \cup \vec{ C }=\vec{ A } \cup C $
$\therefore \text { Equivalence }$
A
$\frac{11 e }{2}+\frac{7}{2 e }-4$
B
$\frac{11 e }{2}+\frac{7}{2 e }$
C
$\frac{13 e }{4}+\frac{5}{4 e }-4$
D
$\frac{13 e }{4}+\frac{5}{4 e }$
Solution
$\displaystyle\sum_{n=1}^{\infty} \frac{2 n^2+3 n+4}{(2 n) !} $
$ \frac{1}{2} \displaystyle\sum_{n=1}^{\infty} \frac{2 n(2 n-1)+8 n+8}{(2 n) !} $
$ \frac{1}{2} \displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n-2) !}+2 \displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n-1) !}+4 \displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n) !}$
$ e =1+1+\frac{1}{2 !}+\frac{1}{3 !}+\frac{1}{4 !}+\ldots . $
$ e ^{-1}=1-1+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}+\ldots .$
$ \left( e +\frac{1}{ e }\right)=2\left(1+\frac{1}{2 !}+\frac{1}{4 !}+\ldots \ldots .\right)$
$ e -\frac{1}{ e }=\left(1+\frac{1}{3 !}+\frac{1}{5 !}+\ldots . .\right)$
Now
$ \frac{1}{2}\left(\displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n-2) !}\right)+2 \displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n-1) !}+4 \displaystyle\sum_{n=1}^{\infty} \frac{1}{(2 n) !} $
$ =\frac{1}{2}\left[\frac{e+\frac{1}{e}}{2}\right]+2\left[\frac{e-\frac{1}{e}}{2}\right]+4\left(\frac{e+\frac{1}{e}-2}{2}\right) $
$ =\frac{\left(e+\frac{1}{e}\right)}{4}+e-\frac{1}{e}+2 e+\frac{2}{e}-4$
$ =\frac{13}{4} e+\frac{5}{4 e}-4$
A
$4\left(\log _{ e } 2\right)^2-2$
B
$8 \log _{ e } 2-2$
C
$4\left(\log _e 2\right)^2+2$
D
$4 \log _{ e } 2+2$
Solution
$ y^{\prime}=x^x $
$ y^{\prime}=x^x(1+\ell n x) $
$ y^{\prime \prime}=x^x(1+\ell n x)^2+x^x \cdot \frac{1}{x} $
$ y^{\prime \prime}(2)=4(1+\ell \operatorname{n} 2)^2+2 $
$y^{\prime}(2)=4(1+\ell n 2) $
$ y^{\prime \prime}(2)-2 y^{\prime}(2)=4(1+\ell \operatorname{n} 2)^2+2-8(1+\ell n 2) $
$ =4(1+\ell n 2)[1+\ell n 2-2]+2 $
$ \left.=4(\ell n 2)^2-1\right)+2 $
$ =4(\ell n 2)^2-2$
A
$\frac{11}{7} \sqrt{2}$
B
$\frac{11}{7}$
C
$\frac{\sqrt{914}}{7}$
D
$\frac{11}{5} \sqrt{2}$
Solution
$ \vec{ a }=2 \hat{ i }-7 \hat{ j }+5 \hat{ k } $
$ \vec{ b }=\hat{ i }+\hat{ k } $
$ \vec{ c }=\hat{ i }+2 \hat{ j }-3 \hat{ k } $
$ \vec{ r } \times \vec{ a }=\vec{ c } \times \vec{ a } \Rightarrow(\vec{ r }-\vec{ c }) \times \vec{ a }=0 $
$ \therefore \vec{ r }=\vec{ c }+\lambda \vec{ a } $
$ \vec{ r } \cdot \vec{ b }=0 \Rightarrow \vec{ c } \cdot \vec{ b }+\lambda \quad \vec{ b } \cdot \vec{ a }=0 $
$ -2+\lambda(7)=0 \Rightarrow \lambda=\frac{2}{7} $
$ \therefore \vec{ r }=\vec{ c }+\frac{2 \vec{ a }}{7}=\frac{1}{7}(11 \hat{ i }-11 \hat{ k }) $
$ \mid \vec{ r }=\frac{11 \sqrt{2}}{7}$
A
$n ( S )=2$ and only one element in $S$ is less than $\frac{1}{2}$.
B
$n(S)=1$ and the element in $S$ is less than $\frac{1}{2}$.
C
$n(S)=1$ and the elements in $S$ is more than $\frac{1}{2}$.
D
$n(S)=0$
Solution
$ 0< x <1 $
$ 2 \tan ^{-1}\left(\frac{1- x }{1+ x }\right)=\cos ^{-1}\left(\frac{1- x ^2}{1+ x ^2}\right) $
$ \tan ^{-1} x =\theta \in\left(0, \frac{\pi}{4}\right) $
$\therefore x =\tan \theta $
$ 2 \tan ^{-1}\left(\tan \left(\frac{\pi}{4}-\theta\right)\right)=\cos ^{-1}(\cos 2 \theta) $
$ 2\left(\frac{\pi}{4}-\theta\right)=2 \theta$
$ \therefore 4 \theta=\frac{\pi}{2} \therefore \theta=\frac{\pi}{8} $
$x =\tan \frac{\pi}{8}$
$ \therefore x =\sqrt{2}-1 \simeq 0.414$
A
It has infinitely many solutions if $\alpha=2$ and $\beta=-1$
B
$x+y+z=\frac{3}{4}$ if $\alpha=2$ and $\beta=1$
C
It has infinitely many solutions if $\alpha=1$ and $\beta=1$
D
It has no solution if $\alpha=-2$ and $\beta=1$
Solution
$\begin{vmatrix}\alpha & 1 & 1 \\ 1 & \alpha & 1 \\ 1 & 1 & \alpha\end{vmatrix}=0$
$ \alpha\left(\alpha^2-1\right)-1(\alpha-1)+1(1-\alpha)=0 $
$ \alpha^3-3 \alpha+2=0 $
$ \alpha^2(\alpha-1)+\alpha(\alpha-1)-2(\alpha-1)=0 $
$ (\alpha-1)\left(\alpha^2+\alpha-2\right)=0 $
$ \alpha=1, \alpha=-2,1 $
$ \text { For } \alpha=1, \beta=1$

$
\Delta_1=\begin{vmatrix}
1 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{vmatrix}=3-1-1 \Rightarrow x =\frac{1}{4}$
$\Delta_2=\begin{vmatrix}
2 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 2
\end{vmatrix}=2-1=1 \Rightarrow y =\frac{1}{4} $
$\Delta_3=\begin{vmatrix}
2 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 1
\end{vmatrix}=2-1=1 \Rightarrow z =\frac{1}{4}
$
For $\alpha=2 \Rightarrow$ unique solution
A
$A ^{30}- A ^{25}=2 I$
B
$A ^{30}= A ^{25}$
C
$A ^{30}+ A ^{25}- A = I$
D
$A ^{30}+ A ^{25}+ A = I$
Solution
$A =\frac{1}{2}\begin{bmatrix}1 & \sqrt{3} \\ -\sqrt{3} & 1\end{bmatrix}$
$A=\begin{bmatrix}
\cos 60^{\circ} & \sin 60^{\circ} \\
-\sin 60^{\circ} & \cos 60^{\circ}
\end{bmatrix}$
If $A=\begin{bmatrix}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{bmatrix}$ Here $\alpha=\frac{\pi}{3}$
$A^2=\begin{bmatrix}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{bmatrix}\begin{bmatrix}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{bmatrix}$
$=\begin{bmatrix}
\cos 2 \alpha & \sin 2 \alpha \\
-\sin 2 \alpha & \cos 2 \alpha
\end{bmatrix}$
$A^{30}=\begin{bmatrix}
\cos 30 \alpha & \sin 30 \alpha \\
-\sin 30 \alpha & \cos 30 \alpha
\end{bmatrix}$
$
A ^{30}=\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}= I$
$A^{25}=\begin{bmatrix}\cos 25 \alpha & \sin 25 \alpha \\ -\sin 25 \alpha & \cos 25 \alpha\end{bmatrix}=\begin{bmatrix}\frac{1}{2} & \frac{\sqrt{3}}{2} \\ \frac{-\sqrt{3}}{2} & \frac{1}{2}\end{bmatrix}$
$ A ^{25}= A $
$ A ^{25}- A =0$
A
Projection of $\vec{a}$ on $\vec{b}$ is $\frac{17}{\sqrt{35}}$ and the direction of the projection vector is same as of $\vec{b}$.
B
Projection of $\vec{a}$ on $\vec{b}$ is $\frac{17}{\sqrt{35}}$ and the direction of the projection vector is opposite to the direction of $\vec{b}$
C
Projection of $\vec{a}$ on $\vec{b}$ is $\frac{-17}{\sqrt{35}}$ and the direction of the projection vector is same as of $\vec{b}$.
D
Projection of $\vec{a}$ on $\vec{b}$ is $\frac{-17}{\sqrt{35}}$ and the direction of the projection vector is opposite to the direction of $\vec{b}$.
Solution
$ \vec{ a }=5 \hat{ i }-\hat{ j }-3 \hat{ k } $
$ \vec{ b }=\hat{ i }-3 \hat{ j }+5 \hat{ k } $
$ \vec{ a } \cdot \hat{ b }=\frac{5-3-15}{\sqrt{35}}=-\frac{-13}{\sqrt{35}}$
A
$p \vee( p \wedge q )$
B
$( p \wedge( p \rightarrow q )) \rightarrow \sim q$
C
$( p \wedge q ) \rightarrow(\sim( p ) \rightarrow q )$
D
$p \rightarrow( p \wedge( p \rightarrow q ))$
Solution
(i) $p \rightarrow( p \Lambda( p \rightarrow q ))$
$(\sim p ) V ( p \Lambda(\sim p V q))$
$(\sim p) V(f V(p \Lambda q))$
$\sim p V ( p \Lambda q )=(\sim p V p ) \Lambda(\sim p Vq )$
$=\sim p V q$
(ii) $( p \Lambda q ) \rightarrow(\sim p \rightarrow q )$
$\sim( p \Lambda q ) V ( p V q )= t$
$\{ a , b , d \} V \{ a , b , c \}= V$
Tautology
(iii) $( p \Lambda( p \rightarrow q )) \rightarrow \sim q$
$\sim( p \Lambda(\sim p V q )) V \sim q =\sim( p \Lambda q ) V \sim q =\sim p V \sim q$
Not tantology
(iv) $p V ( p \Lambda q )= p$
Not tautology.
A
$16 \log _e 2-\frac{14}{3}$
B
$8 \log _e 2-\frac{13}{3}$
C
$8 \log _e 2+\frac{7}{6}$
D
$16 \log _e 2+\frac{7}{3}$
Solution

Area $=\int\limits_1^2\left(x^2-1\right) d x+\int\limits_2^8\left(\frac{8}{x}-1\right) d x$
$ =\left(\frac{x^3}{3}\right)_1^2+8(\ell n x)_2^8-(x)_1^8 $
$ =\frac{7}{3}+8(2 \ell n 2)-7 $
$ =16 \ell n 2-\frac{14}{3}$
A
0
B
-1
C
1
D
3
Solution
$ \alpha x=e^{x^\beta \cdot y^\gamma} $
$ 2 x^2 y \frac{d y}{d x}=1-x \cdot y^2 \,\,\,\, y^2=t $
$ x^2 \frac{d t}{d x}=1-x t $
$ \frac{d t}{d x}+\frac{t}{x}=\frac{1}{x^2} \,\,\,\, \text { I.F. }=e^{\ell n x}=x $
$ t(x)=\int \frac{1}{x^2} \cdot x d x $
$ y^2 \cdot x=\ell n x+C $
$ \therefore 2 \cdot \ell n 2=\ell n 2+C$
$\therefore C =\ell n 2$
Hence, $xy ^2=\ell n 2 x$
$\therefore 2 x = e ^{ x \cdot y ^2}$
Hence $\alpha=2, \beta=1, \gamma=2$
A
$\frac{1}{2}$
B
$-\frac{1}{2}$
C
$1$
D
$-1$
Solution
$ ab <0\left|\frac{1+ ai }{ b + i }\right|=1 $
$|1+ ai |=| b + i |$
$ a^2+1=b^2+1 \Rightarrow a=\pm b \Rightarrow b=-a \,\,\,\,a s\,\, a b<0$
$ (a, b) \text { lies on }|z-1|=|2 z| $
$ l a+i b-1|=2 | a+i b|$
$(a-1)^2+b^2=4\left(a^2+b^2\right) $
$(a-1)^2=a^2=4\left(2 a^2\right) $
$ 1-2 a=6 a^2 \Rightarrow 6 a^2+2 a-1=0 $
$ a=\frac{-2 \pm \sqrt{28}}{12}=\frac{-1 \pm \sqrt{7}}{6}$
$ a=\frac{\sqrt{7}-1}{6} \& b=\frac{1-\sqrt{7}}{6}$
$[a]=0$
$\therefore \frac{1+[ a ]}{4 b }=\frac{6}{4(1-\sqrt{7})}=-\left(\frac{1+\sqrt{7}}{4}\right)$
or $[ a ]=0$
Similarly it is not matching with $a =\frac{-1-\sqrt{7}}{6}$
No answer is matching.
A
$18\left(1+\frac{1}{\sqrt{3}}\right)$
B
$2\left(9+\frac{8}{\sqrt{7}}\right)$
C
34
D
25
Solution
$ 9=x_1< x_2< \ldots \ldots< x_7 $
$ 9,9+d, 9+2 d, \ldots \ldots .9+6 d $
$ 0, d, 2 d, \ldots \ldots .6 d$
$ \overline{ x }_{\text {new }}=\frac{21 d }{7}=3 d $
$ 16=\frac{1}{7}\left(0^2+1^2+\ldots \ldots .+6^2\right) d ^2-9 d ^2$
$=\frac{1}{\not 7}\left(\frac{6 \times \not 7 \times 13}{\not 6}\right) d ^2-9 d ^2$
$ 16=4 d^2 $
$ d^2=4$
$ d=2$
$\bar{x}+x_6=6+9+10+9$
A
$\frac{\pi^2}{12 \sqrt{3}}$
B
$\frac{\pi^2}{6}$
C
$\frac{\pi^2}{3 \sqrt{3}}$
D
$\frac{\pi^2}{6 \sqrt{3}}$
Solution
$I=\int\limits_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \frac{x+\frac{\pi}{4}}{2-\cos 2 x} d x$ (1)
$x \rightarrow- x$
$I=\int\limits_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{-x+\frac{\pi}{4}}{2-\cos 2 x} d x$ (2)
$(1) +(2)$
$2 I =\int\limits_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \frac{\frac{\pi}{2}}{2-\cos 2 x} d x$
$I=\frac{\pi}{4} \cdot 2 \int\limits_0^{\frac{\pi}{4}} \frac{ dx }{2-\cos 2 x} d x$
$ I =\frac{\pi}{4} \cdot 2 \int\limits_0^{\frac{\pi}{4}} \frac{\left(1+\tan ^2 x \right) dx }{2\left(1+\tan ^2 x \right)-\left(1-\tan ^2 x \right)} $
$ I =\frac{\pi}{4} \int\limits_0^1 \frac{ dt }{3 t ^2+1} $
$ \Rightarrow I =\frac{\pi}{2 \sqrt{3}} \tan ^{-1} \sqrt{3} $
$ I =\frac{\pi^2}{6 \sqrt{3}}$
A
$-9$
B
$3$
C
$9$
D
$-3$
Solution
$3 x ^2-4 y ^2=36 \,\,\,\, 3 x +2 y =1$
$ m =-\frac{3}{2} $
$ m =+\frac{\sec \theta 3}{\sqrt{12} \cdot \tan \theta} $
$ \Rightarrow \frac{3}{\sqrt{12}} \times \frac{1}{\sin \theta}=\frac{-3}{2} $
$ \sin \theta=-\frac{1}{\sqrt{3}} $
$ (\sqrt{12} \cdot \sec \theta, 3 \tan \theta) $
$ \left(\sqrt{12} \cdot \frac{\sqrt{3}}{\sqrt{2}},-3 \times \frac{1}{\sqrt{2}}\right) \Rightarrow\left(\frac{6}{\sqrt{2}}, \frac{-3}{\sqrt{2}}\right)$
A
A and B are mutually exclusive
B
the number of favourable cases of the events $A , B$ and $C$ are 15, 6 and 6 respectively
C
$B$ and $C$ are independent
D
the number of favourable cases of the event $( A \cup B ) \cap C$ is 6
Solution
$ \text { A : no. on } 1^{\text {st }} \text { die }<\text { no. on } 2^{\text {nd }} \text { die } $
$ \text { A : no. on } 1^{\text {st }} \text { die }=\text { even } \& \text { no. of } 2^{\text {nd }} \text { die }=\text { odd } $
$ C: \text { no. on } 1^{\text {st }} \text { die }=\text { odd } \& \text { no. on } 2^{\text {nd }} \text { die }=\text { even }$
$ n(A)=5+4+3+2+1=15 $
$n ( B )=9 $
$ n ( C )=9 $
$ n (( A \cup B ) \cap C )=( A \cap C ) \cup( B \cap C ) $
$ =(3+2+1)+0=6$
A
$\frac{7}{3}$
B
$\frac{9}{2}$
C
$\frac{9}{4}$
D
$\frac{7}{4}$
Solution
$ f ( x )+ f \left(\frac{1}{1- x }\right)=1+ x$
$ x =2 \Rightarrow f (2)+ f (-1)=3 $(1)
$ x =-1 \Rightarrow f (-1)+ f \left(\frac{1}{2}\right)=0 $ (2)
$ x =\frac{1}{2} \Rightarrow f \left(\frac{1}{2}\right)+ f (2)=\frac{3}{2} $(3)
$ (1)+(3)-(2) \Rightarrow 2 f (2)=\frac{9}{2} $
$ \therefore f (2)=\frac{9}{4}$
A
$\frac{25}{83}$
B
$\frac{250}{83}$
C
$\frac{15}{53}$
D
$\frac{250}{82}$
Solution
$ P \equiv P_1+\lambda P_2=0 $
$ (2+\lambda) x+(3+2 \lambda) y+(3 \lambda-1) z-2-6 \lambda=0 $
$ \text { Plane } P \text { is perpendicular to } P_3$
$ \therefore \vec{ n } \cdot \vec{ n }_3=0 $
$ 2(\lambda+2)+(2 \lambda+3)-(3 \lambda-1)=0$
$ \lambda=-8 $
$ P \equiv-6 x-13 y-25 z+46=0 $
$ 6 x+13 y +25 z -46=0$
$ \text { Dist from }(-7,1,1)$
$ d =\left|\frac{-42+13+25-46}{\sqrt{36+169+625}}\right|=\frac{50}{\sqrt{830}} $
$ d^2=\frac{50 \times 50}{830}=\frac{250}{83}$
Answer: 81
Solution

Taking three digit
$ 4,5,9,4,4,4 \Rightarrow \frac{5 !}{3 !}=20$
$ 4,5,9,5,5,5 \Rightarrow \frac{5 !}{4 !}=5 $
$4,5,9,9,9,9 \Rightarrow \frac{5 !}{4 !}=5$
$ 4,5,9,4,5,9 \Rightarrow \frac{5 !}{2 ! 2 !}=30 $
$ \text { Total }=81$
Answer: 105
Solution
${ }^{15} C _2=\frac{15 \times 14}{2}=105$
Answer: 4
Solution
$T_6={ }^{ m } C_5\left(10-3^x\right)^{\frac{ m -5}{2}} \cdot\left(3^{ x -2}\right)=21$
${ }^{ m } C _1,{ }^{ m } C _2,{ }^{ m } C _3$ are in A.P.
2. ${ }^{ m } C _2={ }^{ m } C _1+{ }^{ m } C _3$
Solving for $m$, we get
$m =$ 2(rejected), 7
Put in equation (1)
$21. \left(10-3^x\right) \frac{3^x}{9}=21$
$3^x=3^0, 3^2$
$x =0,2$
Sum of the squares of all possible values of $x=4$
Answer: 1
Solution
$T _{ r +1}={ }^{22} C _{ r } \cdot\left( x ^{\frac{2}{3}}\right)^{22- r } \cdot(\alpha)^{ r }, x ^{-3 r } $
$ ={ }^{22} C _{ r } \cdot x ^{\frac{44}{3}-\frac{2 r }{3}-3 r }(\alpha)^{ r } $
$ \frac{44}{3}=\frac{11 r }{3} $
$ r =4 $
${ }^{22} C _4 \cdot \alpha^4=7315 $
$ \frac{22 \times 21 \times 20 \times 19}{24} \cdot \alpha^4=7315$
$\alpha=1$
Answer: 10
Solution
Plane : $8 x + y +2 z =0$
Given line $AB : \frac{ x -2}{5}=\frac{ y -4}{10}=\frac{ z +3}{-4}=\lambda$
Any point on line $(5 \lambda+2,10 \lambda+4,-4 \lambda-3)$
Point of intersection of line and plane
$8(5 \lambda+2)+10 \lambda+4-8 \lambda-6=0$
$\lambda=-\frac{1}{3}$
$C \left(\frac{1}{3}, \frac{2}{3},-\frac{5}{3}\right)$
$L : \frac{ x -1}{-1}=\frac{ y +4}{2}=\frac{ z +2}{3}=\mu$

$ \overrightarrow{ CD }=\left(-\mu+\frac{2}{3}\right) \hat{ i }+\left(2 \mu-\frac{14}{3}\right) \hat{ j }+\left(3 \mu-\frac{1}{3}\right) \hat{ k } $
$ \left(-\mu+\frac{2}{3}\right)(-1)+\left(2 \mu-\frac{14}{3}\right) 2+\left(3 \mu-\frac{1}{3}\right) 3=0 $
$ \mu=\frac{11}{14}$
$ \overrightarrow{ CD }=\frac{-5}{42}, \frac{-130}{42}, \frac{85}{42} $
$ \text { Direction ratios } \rightarrow(-1,-26,17) $
$la + b + cl =10$
Answer: 321
Solution
$ 3,7,11,15, \ldots \ldots \ldots \ldots, 399 \,\,\,\, d _1=4 $
$ 2,5,8,11, \ldots \ldots \ldots \ldots ., 359 \,\,\,\, d _2=3 $
$ 2,7,12,17, \ldots \ldots, 197 \,\,\,\, d_3=5 $
$ \operatorname{LCM}\left( d _1, d _2, d _3\right)=60 $
$ \text { Common terms are 47, 107, } 167$
$ \text { Sum }=321 $
Answer: 26
Solution
$ I=\int\limits_0^\pi \frac{5^{\cos x}\left(1+\cos x \cos 3 x+\cos ^2 x+\cos ^3 x \cos 3 x\right)}{1+5^{\cos x}} d x$
$ I=\int\limits_0^\pi \frac{5^{-\cos x}\left(1+\cos x \cos 3 x+\cos ^2 x+\cos ^3 x \cos 3 x\right)}{1+5^{-\cos x}} d x $
$ 2 I=\int\limits_0^\pi\left(1+\cos x \cos 3 x+\cos ^2 x+\cos ^3 x \cos 3 x\right) d x$
$\not{2} I=\not 2 \int\limits_0^{\frac{\pi}{2}}\left(1+\cos x \cos 3 x+\cos ^2 x+\cos ^3 x \cos 3 x\right) d x$
$I =\int\limits_0^{\frac{\pi}{2}}\left(1+\sin x (-\sin 3 x )+\sin ^2 x -\sin ^3 x \sin 3 x \right) dx$
$ 2 I =\int\limits_0^{\frac{\pi}{2}}\left(3+\cos 4 x +\cos ^3 x \cos 3 x -\sin ^3 x \sin 3 x \right) dx $
$ 2 I =\int\limits_0^{\frac{\pi}{2}} 3+\cos 4 x +\left(\frac{\cos 3 x+3 \cos x }{4}\right) \cos 3 x -\sin 3 x \left(\frac{3 \sin x-\sin 3 x}{4}\right) d x$
$2 I=\int\limits_0^{\frac{\pi}{2}}\left(3+\cos 4 x+\frac{1}{4}+\frac{3}{4} \cos 4 x\right) d x $
$ 2 I=\frac{13}{4} \times \frac{\pi}{2}+\frac{7}{4}\left(\frac{\sin 4 x}{4}\right)_0^{\frac{\pi}{2}} \Rightarrow I =\frac{13 \pi}{16}$
Answer: 16
Solution
$ y^2=8 x+4 y+4$
$ (y-2)^2=8(x+1)$
$ y^2=4 a x$
$ a=2, X=x+1, Y=y-2$
focus $(1,2)$
$y -2= m ( x -1)$
Put $(3,0)$ in the above line $m =-1$
Length of focal chord $=16$
Answer: 6
Solution
Given Equation is not equation of plane as $y y$ is present. If we consider $y$ is $\gamma$ then answer would be 6 .
Normal vector of plane $=3 \hat{i}-\hat{j}-2 \hat{k}$
Plane $: 3 x - y -2 z +\lambda=0$
Point $(3,-2,5)$ satisfies the plane
$ \lambda=-1$
$ 3 x-y-2 z=1$
$ \alpha \beta y=6$
Answer: 39





















