JEE Advanced Physics Question Paper with Solution JEE Advanced 2020 Paper 1
Answer: 4
Solution

$y$ co-ordinate of first image $S^{\prime}$ is ' $y$ '
$\frac{4}{3} \sin i=\sin 45^{\circ} $
$\Rightarrow \sin i=\frac{1}{\sqrt{2}} \frac{3}{4}$

$i \approx 32^{\circ} $
$\therefore \theta=45-i$
So slope of the line passing through $(-12,0)$ is
$m=\tan (45-i)=\frac{1-\tan i}{1+\tan i}$
$\Rightarrow m=\frac{\sqrt{23}-3}{\sqrt{23}+3}$
$\therefore \text { Eq } \Rightarrow y=\frac{(\sqrt{23}-3) x}{\sqrt{23}+3}+\frac{12(\sqrt{23}-3)}{(\sqrt{23}+3)}$
Other equation $y=-x$
Now $ y=\frac{-(\sqrt{23}-3) y}{\sqrt{23}+3}+\frac{12(\sqrt{23}-3)}{(\sqrt{23}+3)} $
$\Rightarrow y=\left(\frac{2 \times 23}{\sqrt{23}+3}\right)=\frac{12(\sqrt{23}-3)}{(\sqrt{23}+3)}$
$2 y=\frac{12(\sqrt{23}-3)}{\sqrt{23}} \approx 4.5 \approx 4$
So, separation between two images is $4\, cm$.
Answer: 9
Solution
The velocity of air flow relative to the train between its sides and the walls of the tunnel is $v$
$v \times 3 S _{ t }= v _{ t } 4 S _{ t }$
$v=\frac{4}{3} v_{t}$ ...... (i)
Now,
$P+\frac{1}{2} \rho v^{2}=P_{0}+\frac{1}{2} \rho v_{t}^{2} $
$P_{0}-P=\frac{1}{2} \rho\left(v^{2}-v_{t}^{2}\right)$
$=\frac{1}{2} \rho v_{t}^{2}\left(\frac{16}{9}-1\right) $
$P_{0}-P=\frac{7}{18} \rho v_{t}^{2} $
Hence $N=9$
Answer: 6
Solution
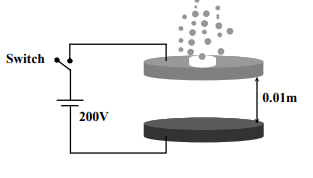
Electric field between the discs after closing the switch
$E=\frac{V}{d}=\frac{200}{0.01}=2 \times 10^{4} N / C$
When an oil drop stops and floats between the discs
$qE = mg$
$neE = mg$
$n=\frac{m g}{e E}=\frac{\rho \frac{4}{3} \pi r^{3} g}{e E}$
$n=900 \times \frac{4 \times 3.14 \times\left(8 \times 10^{-7}\right)^{3} \times 10}{3 \times 1.6 \times 10^{-19} \times 2 \times 10^{4}}$
$n=\frac{3 \times 4 \times 3.14 \times 2 \times 8}{100}=6$
The number of electrons present in this oil drop is $n =6$
Answer: 4
Solution
$\frac{480-N}{480}=\frac{\rho_{2}}{\rho_{1}}$
$1-\frac{N}{480}=e^{-\left(\frac{150-100}{6000}\right)}$
$\Rightarrow 1-\frac{N}{480}=1-\frac{5}{600}$
$N=4$
Answer: 2
Solution

$\frac{m g}{\sin \left(90+\frac{\alpha}{2}\right)}=\frac{2 k q p}{r^{3} \sin \left(180^{\circ}-\alpha\right)}$
$\frac{m g \sin \alpha}{\cos \left(\frac{\alpha}{2}\right)}=\frac{2 k q p}{r^{3}}$
$U_{\text {elec }}=P E=\frac{k q p}{r^{2}}$
$=m g r \sin \left(\frac{\alpha}{2}\right)=m g h$
$U=U_{\text {grav }}+U_{\text {elec }}=2 m g h$
Answer: 6
Solution

Assuming the gas to be an ideal mono-atomic gas
$\therefore C_{v}=\frac{3}{2} R$
and area of cross section to be A.
Initially
$P_{0} 4 A=0.1 R \times 300$ (For both)
Let piston shifts by $\times$ meter and final temperature is $T$.
Then
$P_{2} A(4-x)=0.1 R T$
$\therefore P_{2} A=\frac{0.1 R T}{4-x}=\frac{R T}{10(4-x)}$
And $P_{1} A=\frac{R T}{10(4+x)}$
But finally $P_{2} A-P_{1} A=83$
$=\frac{R T}{10}\left(\frac{1}{4-x}-\frac{1}{4+x}\right)$
$\Rightarrow \frac{R T}{10}\left(\frac{2 x}{16-x^{2}}\right)=83$
$0.2 C_{v} \times 300+m g \cdot x=0.2 C_{v} T$
$\Rightarrow \frac{3}{2} R \times \frac{2}{10} \times 300+83 x=\frac{2}{10} \times \frac{3}{2} R T$
$\Rightarrow \left(\frac{900 R}{10}+83 x\right)=3\left(\frac{R T}{10}\right)$
$\left(\frac{300 R}{10}+\frac{83}{3} x\right)=\frac{R T}{10}$
$\left(30 R+\frac{83 x}{3}\right)\left(\frac{2 x}{16-x^{2}}\right)=83$
$\Rightarrow 83\left(3+\frac{x}{3}\right)\left(\frac{2 x}{16-x^{2}}\right)=83$
$\Rightarrow \frac{(9+x)}{3} \frac{(2 x)}{\left(16-x^{2}\right)}=1$
$\Rightarrow 18 x+2 x^{2}=48-3 x^{2}$
$\Rightarrow 5 x^{2}+18 x-48=0$
$\therefore x=1.78 \approx 2$
So, the distance from top is $6 \,m$.
A
$R =\frac{ h ^{2}+ r ^{2}}{2 h }$
B
$R =\frac{3 r ^{2}}{2 h }$
C
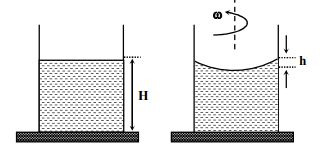
Apparent depth of the bottom of the beaker is close to $\frac{3 H }{2}\left(1+\frac{\omega^{2} H }{2 g }\right)^{-1}$
D
Apparent depth of the bottom of the beaker is close to $\frac{3 H }{4}\left(1+\frac{\omega^{2} H }{4 g }\right)^{-1}$
Solution

$\tan \theta=\frac{d y}{d x}=\frac{\omega^{2} x}{g}$
$\Rightarrow y=\frac{\omega^{2} x^{2}}{2 g} $
$\Rightarrow h=\frac{\omega^{2} r^{2}}{2 g}$
Pythagoras $\Rightarrow r ^{2}+( R - h )^{2}= R ^{2}$
$\Rightarrow R =\frac{ r ^{2}+ h ^{2}}{2 h } $
$\Rightarrow $ A option is correct
For apparent depth applying refraction formula
$\frac{1}{v}-\frac{4}{3(H-h)}=\frac{1-\frac{4}{3}}{R}$
$ \Rightarrow \left|\frac{1}{v}\right|=\frac{1}{3 R}+\frac{4}{3 H}($ as $H > > h )$
$\Rightarrow |v|=\frac{3 H}{4}\left[1+\frac{\omega^{2} H}{4 g}\right] $
$\Rightarrow $ D option is correct.
A
$v _{0}^{2}-2 gh =\frac{1}{2} gR$
B
$v _{0}^{2}-2 gh =\frac{\sqrt{3}}{2} gR$
C
the centripetal force required at points $x$ and $z$ is zero
D
the centripetal force required is maximum at points $x$ and $z$
Solution
Let $v$ be the speed at $y$
Energy conservation $\Rightarrow \frac{1}{2} m v_{0}^{2}=m g h+\frac{1}{2} m v^{2}$ .... (1)
FBD at $y \Rightarrow m g \sin 30^{\circ}=\frac{m v^{2}}{R}$ .... (2)
From (1) and (2)
$\Rightarrow v _{0}^{2}-2 gh =\frac{ gR }{2}$, (A) option is correct.
(D) is true as on the circular path he/she will have maximum speed at $x$ and $z$.
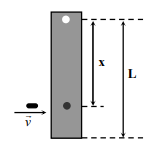
A
$\omega=\frac{3 vX }{ L ^{2}+3 x ^{2}}$
B
$\omega=\frac{12 vx }{ L ^{2}+12 x ^{2}}$
C
$x_{M}=\frac{L}{\sqrt{3}}$
D
$\omega_{ M }=\frac{ V }{2 L } \sqrt{3}$
Solution
Conserving angular momentum about pivot.
$\Rightarrow mvx =\left(\frac{ mL ^{2}}{3}+ mx ^{2}\right) \omega$
$\Rightarrow \omega=\frac{3 vx }{ L ^{2}+3 x ^{2}}$
For $\omega$ to be maximum
$\Rightarrow \frac{d \omega}{d x}=0$,
this gives $x=\frac{L}{\sqrt{3}}$
and $\omega_{\max }=\frac{\sqrt{3} v}{2 L}$
A
the cut-off wavelength will reduce to half, and the wavelengths of the characteristic X-rays will remain the same
B
the cut-off wavelength as well as the wavelengths of the characteristic X-rays will remain the same
C
the cut-off wavelength will reduce to half, and the intensities of all the X-rays will decrease
D
the cut-off wavelength will become two times larger, and the intensity of all the X-rays will decrease
Solution
$\lambda_{c} \propto \frac{1}{V}$, current $\propto$ Intensity
A
electric force between the spheres remains unchanged
B
electric force between the spheres reduces
C
mass density of the spheres is $840 \,kg\, m ^{-3}$
D
the tension in the strings holding the spheres remains unchanged
Solution
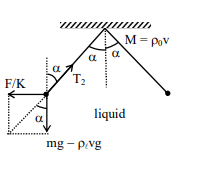
$\tan \alpha=\frac{F}{m g}=\frac{F / K}{m g-\rho_{t} v g} $
$\Rightarrow \rho_{0}=840\, kg / m ^{3} $
$T_{1} \cos \alpha=m g, T_{2} \cos \alpha=m g-\rho_{t} v g$
So, $T _{2}$ will decrease

A
$a _{ x }=1 \,ms ^{-2}$ implies that when the particle is at the origin, $a _{ y }=1 \,ms ^{-2}$
B
$a _{ x }=0$ implies $a _{ y }=1\, ms ^{-2}$ at all times
C
at $t =0$, the particle's velocity points in the $x$-direction
D
$a _{ x }=0$ implies that at $t =1 s$, the angle between the particle's velocity and the $x$ axis is $45^{\circ}$
Solution

$y=\frac{x^{2}}{2}$
$v_{y}=x v_{x}$
$a_{y}=x a_{x}+v_{x}^{2}$
$x=0 \Rightarrow a_{y}=a_{x}^{2}=1 m / s ^{2}$,
for any value of $a_{x}$
$a_{x}=0 \Rightarrow a_{y}=v_{x}^{2}=1$
$a_{x}=0$
$\tan \theta=\frac{v_{x}}{v_{y}}=x=1\left(x=v_{x} t=1\right)$
Answer: 2.05
Solution
In adiabatic process
$dp =-\frac{\gamma p }{ V } dV $
$=-\frac{\gamma p _{0}}{ V }\left(-4 \pi R ^{2} a \right)$
Work done in the process $=-( dp )_{ avg } d V =-\frac{ dp }{2} dV$
$=-\frac{\gamma p _{0}}{2 V }\left(4 \pi R ^{2} a \right)\left(-4 \pi R ^{2} a \right)$
$=\left(4 \pi p _{0} Ra ^{2}\right) \frac{3}{2} \times \frac{41}{30}$
$=(2.05)\left(4 \pi p _{0} Ra ^{2}\right)$
$\Rightarrow x =2.05$
Answer: 0.27
Solution

$R _{3}^{\prime}= R _{3}(1+\alpha \Delta T )=312\, \Omega$
$V _{ S }- V _{ T }= I _{2} R _{2}- L _{1} R _{1}$
$=\frac{50}{100+500} \times 100-\frac{50}{60+312} \times 60$
$\approx 0.2688 \approx 0.27\, V$
Answer: 1.30
Solution
$\frac{1}{ C }=\frac{1}{ C _{1}}+\frac{1}{ C _{2}} $
$\Rightarrow \frac{1}{ C ^{2}} \Delta C =\frac{1}{ C _{1}^{2}} \Delta C _{1}+\frac{1}{ C _{2}^{2}} \Delta C _{2}$
$\Rightarrow \frac{\Delta C }{ C }= C \left(\frac{\Delta C _{1}}{ C _{1}^{2}}+\frac{\Delta C _{2}}{ C _{2}^{2}}\right)$
$=1200\left(\frac{10}{4 \times 10^{6}}+\frac{15}{9 \times 10^{6}}\right)=5 \times 10^{-3}$
Energy stored
$U =\frac{1}{2} CV ^{2} \Rightarrow \frac{\Delta U }{ U }=\frac{\Delta C }{ C }+2 \frac{\Delta V }{ V }$
Percentage error in energy stored in the combination of capacitors.
$\frac{\Delta U}{U} \times 100=\left(5 \times 10^{-3}+2 \frac{0.02}{5}\right) \times 100=1.30 \%$
Answer: 0.238
Solution
$B =- V \frac{ dP }{ dV }$
$70 \times 10^{9}=\frac{(1)^{3} \times 5 \times 10^{3} \times 10}{\Delta V }$
$\Rightarrow \Delta V=\frac{5}{7} \times 10^{-3}$
$\Rightarrow \frac{\Delta V}{V}=\frac{3 \Delta \ell}{\ell}$
$\Rightarrow \Delta \ell=\frac{5}{21}=0.238 \,mm$
Answer: 55
Solution

$dU =\phi_{1} di _{1}+\phi_{2} di _{2}$
$U =\frac{1}{2} L _{1} l _{1}^{2}+\frac{1}{2} L _{2} l _{2}^{2} \pm Ml _{1} l _{2}=55 \,mJ$
Answer: 8.33
Solution

When steady state is reached energy received per unit time is equal to energy loss per unit time
$700 \times 0.05= ms \frac{ d \Delta T }{ dt } $
$\frac{ d \Delta T }{ dt }=- b \Delta T$
$\Delta T =8.33 \,K$
JEE Advanced Chemistry Question Paper with Solution JEE Advanced 2020 Paper 1
Answer: 9
Solution
Since I.E. of $Na$ is $495.8 \,kJ \,mol ^{-1}$,
so $( n +2)$ should be $11$ .
$n +2=11$, So $n =9$
Answer: 6
Solution
Only polar molecules can be attracted by a charged comb. So, except $O _{2}, CCl _{4}$ and $C _{6} H _{6}$ all can be attracted in electric field.
Answer: 6
Solution
In slightly alkaline medium, $MnO _{4}^{-}$reduces to $MnO _{2}$ while $I$ is oxidized to $I _{2}$.
$\left. MnO _{4}^{-}+2 H _{2} O +3 e ^{-} \longrightarrow MnO _{2}+4 OH ^{-}\right) \times 2$
$\left.2 I ^{-} \longrightarrow I _{2}+2 e ^{-}\right) \times 3$
$2 \,MnO _{4}^{-}+6 I ^{-}+4 H _{2} O \longrightarrow 2 MnO _{2}+3 I _{2}+8 OH ^{-}$
So, $2\, mol$ of $KMnO _{4}$ can produce $3\, mole$ of $I _{2}$
$\therefore 4 \,mol$ of $KMnO _{4}$ can produce $6$ mole of $I _{2}$
Answer: 4
Solution
$CrO_4^{2-} \ce{<=>[H^+][OH]} Cr_2O_7^{2-}$
$Cr_2O_7^{2-} + H_2O + H^+ \rightarrow \underset{\text{Chromium peroxide(blue)}}{CrO_5}$

So, number of oxygen atoms attached to $Cr$ through single bond $= 4$
Answer: 5
Solution
At $pH = 2$ (highly acidic), the structure of the peptide will be as shown below.

So, $|Z_1| = 2$
At $pH = 6$ it will exist as neutral or zwitter-ion structure as shown below.

So, according to this condition, $|Z_2| = 0$
At $pH = 11$ (highly basic), the given peptide will exist as:

So, $\left|Z_{3}\right|=|-3|=3$
$\left|Z_{1}\right|+\left|Z_{2}\right|+\left|Z_{3}\right| =2+0+3=5$
Answer: 6
Solution
Since given compound produces pink colour with neutral $FeCl _{3}$.
So, it must have at least one $- OH$ group attached to benzene ring.
Also, given compound is optically active, it means it should have a chiral centre, which is only possible when it has - $CH ( OH ) CH _{3}$
So, based on the above observations, compound $\left( C _{8} H _{10} O _{2}\right)$ is expected to possess the following isomeric structures.

So, total isomeric structures $= 6$
A
If $X$ is $H _{2} O (l)$, deflection of the pan is upwards.
B
If $X$ is $K _{4}\left[ Fe ( CN )_{6}\right]$ (s), deflection of the pan is upwards.
C
If $X$ is $O _{2}(g)$, deflection of the pan is downwards.
D
If $X$ is $C _{6} H _{6}(I)$, deflection of the pan is downwards.
Solution
Diamagnetic (all electrons paired) are repelled i.e. magnetized in opposite direction in magnetic field, so such substance are deflected upwards in magnetic field. Diamagnetic substances are
$H _{2} O (\ell), K _{4}\left[ Fe ( CN )_{6}\right], C _{6} H _{6}(\ell)$
Paramagnetic substances (at least one unpaired electron) are attracted in magnetic field, so such substances are deflected downwards.
$O _{2}( g ): \sigma_{1 s ^{2}} \sigma_{1 s ^{2}}^{*} \sigma_{2 s ^{2}} \sigma_{2 p _{x}^{2}} \pi_{2 p _{x}^{2}}=\pi_{2 p _{y}^{2}} \pi_{2 p _{x}^{1}}^{*}=\pi_{2 p _{y}^{1}}^{*}$
Since $O _{2}$ molecules has two unpaired electrons in antibonding $\pi$. MO.
So, $O _{2}$ is paramagnetic.
A
B
C
D
Solution

The order of the above reaction is one $\left( S _{ N } 1\right)$ because substrate is a $3^{0}$-halide
So, for a first order reaction.
$P=P_{0} \times e^{-k t}$ or $\frac{P}{P_{0}}=e^{-k t}$
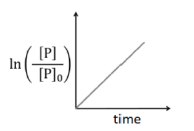
$\ln \left(\frac{P}{P_{0}}\right)=-k t$
$y = mx$
So, the slope of the graph $\ln \left(\frac{ P }{ P _{0}}\right)$ versus time ( $t$ ) should be negative.
Hence option D is incorrect.

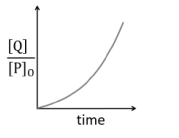
Also $\frac{ P }{ P _{0}}= e ^{- kt } $
$\left(1-\frac{ P }{ P _{0}}\right)=\left(1- e ^{- kt }\right)$
$\frac{ P _{0}- P }{ P _{0}}=\left(1- e ^{- kt }\right)$
Or $ \frac{[Q]}{P_{0}}=\left(1-e^{-k t}\right)$
So, graph between $\frac{[ Q ]}{ P _{0}}$ Vs. $t$, should be as shown in figure (1), so, option (C)is incorrect

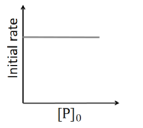
For a first order reaction
$ r = k [ P ]^{1} $
At $ t =0, r _{ i }= k \left[ P _{0}\right]$
So, initial rate of reaction is directly proportional to initial conc. of $P$.
Hence option B is also incorrect.

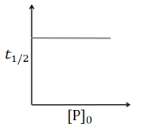
For a first order reaction
$t _{1 / 2}=\frac{\ln 2}{ k }\left[ P _{0}\right]^{0}$
So, $t _{1 / 2}$ is independent of initial conc. of reactant.
So, option (A) is correct.
A
Hydrated $Al _{2} O _{3}$ precipitates, when $CO _{2}$ is bubbled through a solution of sodium aluminate.
B
Addition of $Na _{3} AlF _{6}$ lowers the melting point of alumina.
C
$CO _{2}$ is evolved at the anode during electrolysis.
D
The cathode is a steel vessel with a lining of carbon.
Solution
Sodium meta aluminate is precipitated in the form of $Al ( OH )_{3}$ or $Al _{2} O _{3} \cdot xH _{2} O$.
i.e hydrated aluminium hydroxide by passing $CO _{2}$ gas.
$2 NaAlO _{2}+ CO _{2}( g )+3 H _{2} O (\ell) \longrightarrow \underset{ Or Al _{2} O _{3} \cdot kH _{2} O }{2 Al ( OH )_{3} } \downarrow+ Na _{2} CO _{3}$
In electrolytic reduction of $Al _{2} O _{3}$ by Hall-Haroult process,
cryolite $\left( Na _{3} AlF _{6}\right)$ and fluorspar $\left( CaF _{2}\right)$ are added in order to reduce the melting temperature of $Al _{2} O _{3}$.
Anode is made up of graphite,
So, $C ( s )+2 O ^{2-} \longrightarrow CO _{2}( g )+4 e ^{-}$
Cathode is a steel vessel lined with graphite.
A
$SnCl _{2} .2 H _{2} O$ is a reducing agent.
B
$SnO _{2}$ reacts with $KOH$ to form $K _{2}\left[ Sn ( OH )_{6}\right]$.
C
$A$ solution of $PbCl _{2}$ in $HCl$ contains $Pb ^{2+}$ and $Cl ^{-}$ions.
D
The reaction of $Pb _{3} O _{4}$ with hot dilute nitric acid to give $PbO _{2}$ is a redox reaction.
Solution
(A) $Sn ^{2+}$ is less stable than $Sn ^{4+}$,
therefore $SnCl _{2} \cdot 2 H _{2} O$ is a Lewis acid.
(B) $SnO _{2}$ is amphoteric, so it will dissolve in $KOH$ solution forming $K _{2} SnO _{3}$ or $K _{2}\left[ Sn ( OH )_{6}\right]$.
$SnO _{2}+2 KOH +2 H _{2} O \longrightarrow K _{2}\left[ Sn ( OH )_{6}\right]$
(C) $PbCl _{2}$ will form a complex with $HCl$
$PbCl _{2}( s )+2 HCl \longrightarrow H _{2}\left[ PbCl _{4}\right]$
So, we may assume that now this complex will dissociate as:
$H _{2}\left[ PbCl _{2}\right] \longrightarrow 2 H ^{+}+\left[ PbCl _{4}\right]^{2-}$
So, considering this possibility, option (C) should be incorrect.
(D) $Pb_3O_4$ reacts with conc.$HNO_3$ to form $PbO_2$ but the reaction is not a redox reaction.
$\overset{(+4)}{PbO_2}.\overset{(+2)}{2PbO} + \underset{\text{Conc.}}{4HNO_3} \rightarrow \overset{(+4)}{PbO_2}\downarrow + \overset{(+2)}{2Pb}(NO_3)_2 + 6H_2O$
or
$Pb_3O_4$
So, option (D) is incorrect.
A
The order of basicity is II > I > III > IV.
B
The magnitude of $pK _{ b }$ difference between I and II is more than that between III and IV.
C
Resonance effect is more in III than in IV.
D
Steric effect makes compound IV more basic than III.
Solution
$\bullet$ (III) is the weakest base due to the presence of three $- NO _{2}$ group, which exert strong $- M$ effect.
$\bullet$ In compound (IV)  group is thrown out of the plane of aromatic ring due to steric crowding by $- NO _{2}$ groups at ortho positions as a result of this lone pair of electron on $N$-atom does not participate in resonance with aromatic ring and hence it acts as an aliphatic amine. So, (IV) is the strongest base.
group is thrown out of the plane of aromatic ring due to steric crowding by $- NO _{2}$ groups at ortho positions as a result of this lone pair of electron on $N$-atom does not participate in resonance with aromatic ring and hence it acts as an aliphatic amine. So, (IV) is the strongest base.
$\bullet$ Correct order of basicity is; III $< I < II < IV$ (in basic character).
$\bullet$ Difference of $pK_a$ values is highest between (III) and (IV).
$\bullet$ $pK _{ b } ;$ (I) $\rightarrow 9.42 ;$ (II) $\rightarrow 8.94$, (IV) $\rightarrow 4.60$
A
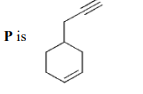
B
$X$ is $Pd - C /$ quinoline $/ H _{2}$
C
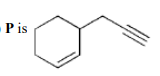
D
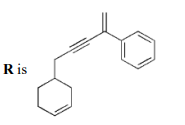
Solution
$\bullet$ On the basis of the given conditions, correct structure of $(P)$ should be

as explained below:

$\bullet$ 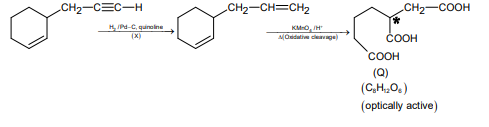
Answer: 03.00
Solution

$\underset{\text { (weak base) }}{ B }+\underset{\text { (strong acid) }}{ HA } \longrightarrow BH ^{+}+ A ^{-}$
From the graph, it is clear, that the equivalence point is reached at a titre value of $6 \,mL$
i.e. when $6 \,mL$ of HA are added base (B) is completely neutralized.
So it will be half neutralized at titre value of $3 \,mL$;
when $3\, mL$ of HA is added, 'B' is half-neutralized.
So at this stage it will form a best buffer.
i.e. $pOH = pK _{ b }=3$
So, $pK _{ b }$ of weak base $=3$
Answer: 0.20
Solution
$0.3=p_{A}^{0} \times 0.25+p_{B}^{0} \times 0.75 $ .... (1)
$0.4=p_{A}^{0} \times 0.50+p_{B}^{0} \times 0.50$ .... (2)
On solving, $p _{ B }^{0}=0.20$ bar and $p _{ A }^{0}=0.6$ bar
Answer: -5246.50
Solution
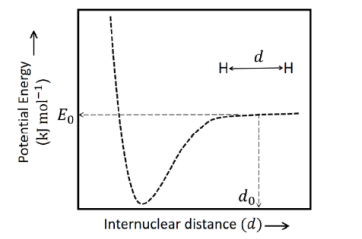
P.E. $=-\frac{ Kq _{1} q _{2}}{ r }$
P.E. of one $H -$ atom in ground state $=-\frac{ K ( e )( e )}{ r }$
P.E. $=\frac{-9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{0.529 \times 10^{-10}}$
$=-43.5538 \times 10^{-19} J / atom$
So, P.E. of two $H$ - atoms (or one molecules of $H _{2}$ ) $=-2 \times 43.5538 \times 10^{-19}$
$=-87.106 \times 10^{-19} J /$ molecule
So, P.E. of one mole of $H _{2}$ molecules $=-87.106 \times 10^{-19} \times 6.023 \times 10^{23} J$
$=-524.6490 \times 10^{4} $
$=-5246.49 \,kJ / mol ^{-1} $
$\approx-5246.50 \,kJ\,mol ^{-1}$
Answer: 18.60
Solution

Moles of $P=\frac{9.3}{93}=0.1=$ moles of $Q$.
So, mass of $(Q)=0.1 \times 248 \times 0.75=18.60$ gram
Answer: 935
Solution
$SnO _{2}( s )+ C ( s ) \longrightarrow Sn ( s )+ CO _{2}( g )$
$\Delta H _{ r }^{0}=-394.0+581=187 \,kJ\,mol ^{-1}$
$\Delta S^{0}=210+52-6-56=200 \,J\,mol ^{-1} K ^{-1}$
Equilibrium temperature $( T )_{\text {eq }}=\frac{187 \times 1000}{200}=935 \,K$
So, $T >935\, K$ (for spontaneity)
Answer: 0.20
Solution
$Zn S ( s ) \rightleftharpoons Zn ^{2+}( aq )+ S ^{2}( aq )$
$\left[ S ^{2-}\right]=\frac{ K _{ sp }}{\left[ Zn ^{2+}\right]}=\frac{1.25 \times 10^{-22}}{0.05}=25 \times 10^{-22}$
$ H _{2} S \rightleftharpoons 2 H ^{+}+ S ^{2-} $
$10^{-21}=\frac{\left[ H ^{+}\right]^{2} \times 25 \times 10^{-22}}{0.1} $
${\left[ H ^{+}\right]^{2}=\frac{10^{-22} \times 10^{22}}{25}=\frac{1}{25}} $
${\left[ H ^{+}\right]=\frac{1}{5}=0.20\, M }$
JEE Advanced Mathematics Question Paper with Solution JEE Advanced 2020 Paper 1
Answer: 8
Solution
$ z ^{4}-| z |^{4}=4 i z ^{2} $
$ z ^{4}- z ^{2} \cdot \overline{ z }^{2}=4 i z ^{2}$
$ \Rightarrow z ^{2}=0$ or $z ^{2}-\overline{ z }^{2}=4 i$
Let $ z = x + iy $
$ \Rightarrow ( z +\overline{ z })( z -\overline{ z })=4 i $
$ \Rightarrow 2 x \cdot 2 iy =4 i $
$\Rightarrow xy =1 $
$ z _{1} $ lies on $xy =1 $ in first quadrant
and $z _{2} $ lies on $ xy =1$ in third quadrant.
$ \Rightarrow \left| z _{1}- z _{2}\right|^{2} $ is minimum
when $ z _{1} \equiv(1,1) $ and $ z _{2}=(-1,-1)$
$ \Rightarrow \left| z _{1}- z _{2}\right|^{2}=8$
Answer: 6
Solution
Let ' $n$ ' be the number of missiles fired
$\Rightarrow $ probability of at least $3$ successful hits
$=1-{ }^{n} C_{0}\left(\frac{1}{4}\right)^{n}-{ }^{n} C_{1}\left(\frac{3}{4}\right)\left(\frac{1}{4}\right)^{n-1}-{ }^{n} C_{2}\left(\frac{3}{4}\right)^{2}\left(\frac{1}{4}\right)^{n-2}$
$\Rightarrow 1-{ }^{n} C_{0}\left(\frac{1}{4}\right)^{n}-{ }^{n} C_{1}\left(\frac{3}{4}\right)\left(\frac{1}{4}\right)^{n-1}-{ }^{n} C_{2}\left(\frac{3}{4}\right)^{2}\left(\frac{1}{4}\right)^{n-2} \geq 0.95 $
$\Rightarrow 9 n^{2}-3 n+2 \leq \frac{4^{n}}{10} $
$\Rightarrow $ minimum value of '$n$' is '$6' (n \in N)$
Answer: 2
Solution
Let $R(h, k)$ be point of intersection of tangents at $P$ and $Q$ on $x^{2}-y^{2}=r^{2}$
$\Rightarrow $ equation of chord of contact PQ is $x h+y k=r^{2}$
Which is also $2 x+4 y=5$
$\Rightarrow ( h , k ) \equiv\left(\frac{2 r ^{2}}{5}, \frac{4 r ^{2}}{5}\right)$
Mid-point of OR is circum-centre of $\triangle OPQ$
$\Rightarrow \left(\frac{r^{2}}{5}, \frac{2 r^{2}}{5}\right)$ lies on $x+2 y=4 \Rightarrow r=2$
Answer: 5
Solution
Let $A=\begin{bmatrix}a & b \\ c & d\end{bmatrix}, a+d=3$
$\Rightarrow A^{2}=\begin{bmatrix}a & b \\ c & d\end{bmatrix} \begin{bmatrix}a & b \\ c & d\end{bmatrix}=\begin{bmatrix}a^{2}+b c & a b+b d \\ a c+c d & b c+d^{2}\end{bmatrix}$
$\Rightarrow A^{3}=\begin{bmatrix}a^{3}+2 a b c+b c d & a^{2} b+a b d+b^{2} c+b d^{2} \\ a^{2} c+a c d+b c^{2}+c d^{2} & a b c+2 b c d+d^{3}\end{bmatrix}$
$\Rightarrow a^{3}+d^{3}+3 a b c+3 b c d=-18$
$\Rightarrow (a+d)\left(a^{2}+d^{2}-a d\right)+3 b c(a+d)=-18$
$\Rightarrow (a+d)\left((a+d)^{2}-3 a d\right)+3 b c(a+d)=-18$
$\Rightarrow 3(9-3 a d)+9 b c=-18$
$\Rightarrow a d-b c=5$
$\Rightarrow |A|=5$
Answer: 4
Solution
$f(x)=|2 x-1|+|2 x+1|$
$g(x)=\{x\}$
$f(g(x))=\begin{cases} 2 & -1 < x < -\frac{1}{2} \\ 4 x+4 & -\frac{1}{2} \leq x < 0 \\ 2 & 0 \leq x < \frac{1}{2} \\ 4 x & \frac{1}{2} \leq x < 1\end{cases}$
$\Rightarrow $ Dis-continuous at $x=0 \Rightarrow c=1$
$\Rightarrow $ non-differentiable at $x=-\frac{1}{2}, 0, \frac{1}{2}$
$ \Rightarrow d=3$
$\Rightarrow c+d=4$
Answer: 8
Solution
$\displaystyle\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{4 \sqrt{2} \cdot 2 \sin 2 x \cos x}{2 \sin 2 x \sin \frac{3 x}{2}+\left(\cos \frac{5 x}{2}-\cos \frac{3 x}{2}\right)-\sqrt{2}(1+\cos 2 x)}\right) $
$\Rightarrow \displaystyle\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{16 \sqrt{2} \sin x \cos ^{2} x}{8 \sin x \sin \frac{x}{2} \cdot \cos ^{2} x-2 \sqrt{2} \cos ^{2} x}\right)$
$\Rightarrow \displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \frac{16 \sqrt{2} \sin x}{8 \sin x \sin \frac{x}{2}-2 \sqrt{2}}=8$
A
If $b>0$, then $f$ is an increasing function
B
If $b<0$, then $f$ is a decreasing function
C
$f ( x ) f (- x )=1$ for all $x \in R$
D
$f(x)-f(-x)=0$ for all $x \in R$
Solution
$f'(x)=\frac{f(x)}{b^{2}+x^{2}} $
$ \Rightarrow \int \frac{f^{\prime}(x) d x}{f(x)}=\int \frac{d x}{b^{2}+x^{2}} $
$\Rightarrow \ell n|f(x)|=\frac{1}{b} \tan ^{-1}\left(\frac{x}{b}\right)+c$
As $f (0)=1 \Rightarrow \ell n |1|=0+ c \Rightarrow c =0$
$\Rightarrow f ( x )= e ^{\frac{1}{b} \tan ^{-1}\left(\frac{x}{b}\right)}$
$\Rightarrow f ( x ) \cdot f (- x )=1$,
Also $f ( x )$ is increasing $\forall b \in R$.
A
$1 < e < \sqrt{2}$
B
$\sqrt{2} < e < 2$
C
$\Delta= a ^{4}$
D
$\Delta=b^{4}$
Solution

As in first quadrant if normal at $P$ is making equal intercepts on axes,
then slope of the normal $=-1$
$\Rightarrow $ slope of tangent $=1$
$\Rightarrow $ equation of tangent at $P: \frac{y-0}{x-1}=1$
and equation of tangent at $\left(x_{1}, y_{1}\right): \frac{x x_{1}}{a^{2}}-\frac{y y_{1}}{b^{2}}=1$
$\Rightarrow x _{1}= a ^{2}$ and $y _{1}= b ^{2}$
$ \Rightarrow P \left( x _{1}, y _{1}\right) \equiv P \left( a ^{2}, b ^{2}\right)$
$\Rightarrow $ equation of normal at $P: x+y=a^{2}+b^{2}$
$\Rightarrow B \equiv\left( a ^{2}+ b ^{2}, 0\right)$
$\Rightarrow \Delta=\frac{1}{2} \times b^{2} \times\left(a^{2}+b^{2}-1\right)$
$=\frac{1}{2} \times b^{2} \times 2 b^{2}=b^{4} $
$\Rightarrow \Delta=b^{4}$
$\left(\because\left(a^{2}, b^{2}\right)\right.$ lies on $\left.\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \Rightarrow a^{2}-b^{2}=1\right)$
Also $e=\sqrt{1+\frac{b^{2}}{a^{2}}}=\sqrt{\frac{a^{2}+b^{2}}{a^{2}}}$
$\Rightarrow e=\sqrt{\frac{2 a^{2}-1}{a^{2}}} $
$\Rightarrow e=\sqrt{2-\frac{1}{a^{2}}}$
$ \Rightarrow 1 < e < \sqrt{2}$
$\Rightarrow e \in(1, \sqrt{2})$
A
$f$ is differentiable at every $x \in R$
B
If $g(0)=1$, then $g$ is differentiable at every $x \in R$
C
The derivative $f^{\prime}(1)$ is equal to $1$
D
The derivative $f^{\prime}(0)$ is equal to $1$
Solution
$f(x)=x \cdot g(x) \forall x \in R$
$\Rightarrow \displaystyle\lim _{x \rightarrow 0} f(x)=\left(\displaystyle\lim _{x \rightarrow 0} x\right)\left(\displaystyle\lim _{x \rightarrow 0} g(x)\right)$
$\Rightarrow \displaystyle\lim _{x \rightarrow 0} f(x)=0$
Also $\displaystyle\lim _{x \rightarrow 0}(f(x+y))=\displaystyle\lim _{x \rightarrow 0}(f(x)+f(y)+f(x) \cdot f(y))$
$\Rightarrow \displaystyle\lim _{x \rightarrow 0} f(x+y)=f(y)$
$\Rightarrow f(x)$ is continuous $\forall x \in R$
$\Rightarrow f(0)=0$
$f^{\prime}(x)=\displaystyle\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $
$\Rightarrow f^{\prime}(x)=\displaystyle\lim _{h \rightarrow 0} \frac{f(h)+f(x) \cdot f(h)}{h} $
$\Rightarrow f^{\prime}(x)=\displaystyle\lim _{h \rightarrow 0} \frac{f(h)}{h} \cdot(1+f(x)) $
$\Rightarrow \int \frac{f^{\prime}(x) d x}{1+f(x)}=\int 1 d x$
$\Rightarrow \ln |1+f(x)|=x+c$
$ f(0)=0 \Rightarrow c=0$
$\Rightarrow f(x)=e^{x}-1$
$\Rightarrow f^{\prime}(x)=e^{x}$
$\Rightarrow f(x)$ is differentiable and $f^{\prime}(0)=1$
Also $g(x)=\frac{f(x)}{x}, x \neq 0$
Now if $g(0)=1$
$\Rightarrow g(x)=\begin{cases}\frac{e^{x}-1}{x}, & x \neq 0 \\ 1, & x=0\end{cases} $
$\Rightarrow g(x)$ is continuous at $x=0$
$\Rightarrow g^{\prime}(0)=\displaystyle\lim _{h \rightarrow 0} \frac{g(0+h)-g(0)}{h}$
$=\displaystyle\lim _{h \rightarrow 0} \frac{\frac{e^{h}-1}{h}-1}{h}=\frac{1}{2}$
$\Rightarrow g ( x )$ is diff. $\forall x \in R$ if $g (0)=1$
A
$\alpha+\beta=2$
B
$\delta-\gamma=3$
C
$\delta+\beta=4$
D
$\alpha+\beta+\gamma=\delta$
Solution
Direction ratio of line joining $(3,2,-1) \&(1,0,-1)$ is $(2,2,0)$ proportional to $(\alpha, \beta, \gamma)$
$\Rightarrow \gamma=0, \alpha+\gamma=1, \alpha=1, \beta=1$
So plane $x+y=\delta(2,1,-1)$ satisfies if $\delta=3$
A
$a+b=4$
B
$a-b=2$
C
The length of the diagonal $PR$ of the parallelogram $PQRS$ is $4$
D
$\vec{ w }$ is an angle bisector of the vectors $\overrightarrow{ PQ }$ and $\overrightarrow{ PS }$
Solution
$\vec{ u }=\frac{( a \hat{ i }+ b \hat{ j }) \cdot(\hat{ i }+\hat{ j }) \widehat{ PQ }}{\sqrt{ a ^{2}+ b ^{2}}}, \vec{ v }=\frac{( ai - b \hat{ j }) \cdot(\hat{ i }+\hat{ j }) \widehat{ PS }}{\sqrt{ a ^{2}+ b ^{2}}}$
Given $|\vec{ u }|+|\vec{ v }|=|\vec{ w }|$
$\Rightarrow |a+b|+|a-b|=\sqrt{2\left(a^{2}+b^{2}\right)} $
$=(2 a)^{2}=2\left(a^{2}+b^{2}\right)$
$ a^{2}=b^{2}$
$a \ge b$ or $a \le b$
Area $a ^{2}|(\hat{ i }+\hat{ j }) \times(\hat{ i }-\hat{ j })|=8, a =2$
Diagonal $4 i$ or $4 j$
A
$g ( m , n )= g ( n , m )$ for all positive integers $m , n$
B
$g ( m , n +1)= g ( m +1, n )$ for all positive integers $m , n$
C
$g (2 m , 2 n )=2 g ( m , n )$ for all positive integers $m , n$
D
$g (2 m , 2 n )=( g ( m , n ))^{2}$ for all positive integers $m , n$
Solution
$f ( m , n , p )=\displaystyle\sum_{ i =0}^{p}\left({ }^{m} C_{i}{ }^{n+i} C_{p}{ }^{p+n} C_{p-i}\right)$
$=\displaystyle\sum_{i=0}^{p}\left(\frac{m !}{i !(m-1) !} \cdot \frac{(n+i) !}{p !(n+i-p) !} \cdot \frac{(p+n) !}{(p-i) !(n+i) !}\right)$
$=\displaystyle\sum_{i=0}^{p}{ }^{m} C_{i} \cdot{ }^{n+p} C_{n} \cdot{ }^{n} C_{p-i}$
$={ }^{n+p} C_{n} \cdot{ }^{m+n} C_{p}$
$g\left(m_{1} n\right)=\displaystyle\sum_{p=0}^{m+n} \frac{{ }^{m+n} C_{p}{ }^{n+p} C_{n}}{{ }^{n+p} C_{p}}=\sum_{p=0}^{m+n}{ }^{m+n} C_{p}$
$=2^{m+n} .$
Answer: 495.00
Solution
We need to put $4$ stick (identical) between $11$ balls (identical) such that no $2$ stick are together
${ }^{12} C _{4}=495$
Answer: 1080.00
Solution
Two rooms accommodate two persons each other two room have one person each.
Total ways $\frac{6 !}{(2 !)^{2}(1 !)^{2} 2 ! 2 !} \times 4 !=1080$
Answer: 8.00
Solution
Sum is perfect square if die's show $\{(1,3)(3,1)(2,2)(3,6)(6,3)(4,5)(5,4)\}$
so probability sum is $9$ when it is perfect square $p=4 / 7$
$14 \,p=8$
Answer: 19.00
Solution
$\displaystyle\sum_{r=1}^{39} f\left(\frac{r}{40}\right)=\frac{1}{2} \displaystyle\sum_{r=1}^{39} f\left(\frac{r}{40}\right)+f\left(\frac{40-r}{40}\right)=\frac{39}{2}$
As $(f(x)+f(1-x)=1) \& f\left(\frac{1}{2}\right)=\frac{1}{2}$
So $\displaystyle\sum_{r=1}^{39} f\left(\frac{r}{40}\right)-f\left(\frac{1}{2}\right)=\frac{39}{2}-\frac{1}{2}=19$
Answer: 4.00
Solution
$\int\limits_{0}^{\pi}\left(f^{\prime}(x)+F(x)\right) \cos x d x$
$\int\limits_{0}^{\pi}\left[F^{\prime \prime}(x) \cos x-F^{\prime}(x) \sin x+F^{\prime}(x) \sin x+F(x) \cos x\right] d x$
$=\int\limits_{0}^{\pi}\left(F^{\prime}(x) \cos x+F(x) \sin x\right)$
$=-F^{\prime}(\pi)-F^{\prime}(0)=-f^{\prime}(\pi)-f(0)=2$
$ f(0)=4$
Answer: 0.5