JEE Main Question Paper with Solution 2023 January 24th Shift 2 - Evening

A

-1

B

2

C

3

D

1

Solution

$ \vec{P} \cdot \vec{Q}=0 $
$(\hat{i}+2 m \hat{j}+m \hat{k}) \cdot(4 \hat{i}-2 \hat{j}+m \hat{k})-0 $
$ \Rightarrow 4-4 m+m^2=0 $
$ \Rightarrow(m-2)^2=0 \Rightarrow m=2$

A

$\frac{21}{25}$

B

$\frac{25}{21}$

C

$\frac{35}{27}$

D

$\frac{27}{35}$

Solution

For monoatomic gas $\gamma_1=\frac{5}{3}$
For diatomic gas at low temperatures
$\gamma_2=\frac{7}{5} $
$ \therefore \frac{\gamma_1}{\gamma_2}=\frac{\frac{5}{3}}{\frac{7}{5}}=\frac{25}{21}$

A

Statement I is correct but statement II is incorrect

B

Both Statement I and Statement II are incorrect

C

Both Statement I and II are correct

D

Statement I is incorrect but statement II is correct

Solution

$g ^{\prime}=\frac{ g }{\left(1+\frac{ h }{ R }\right)^2} $
$g ^{\prime}= g \left\{1-\frac{ d }{ R }\right\}$

Statement I is correct & Statement II is incorrect

A

$\frac{2 \lambda}{\epsilon_0}$

B

$\frac{\lambda}{2 \epsilon_0}$

C

$\frac{\lambda}{4 \epsilon_0}$

D

$\frac{\lambda}{\epsilon_0}$

Solution

Potential at centre
$ V=\frac{\left(\lambda \cdot \pi R_2\right)}{4 \pi \varepsilon_0 R_2}+\frac{\left(\lambda \cdot \pi R_1\right)}{4 \pi \varepsilon_0 R_1} $
$=\frac{\lambda}{2 \varepsilon_0}$

A

A-II, B-III, C-I, D-IV

B

A-II, B-I, C-IV, D-III

C

A-IV, B-III, C-I, D-II

D

A-I, B-III, C-II, D-IV

Solution

AM Broadast $\rightarrow 540-1600\, KHz$
FM Broadcast $\rightarrow 88-108\, MHz$
Television $\rightarrow 54-890 \,MHz$
Salellite communication $\rightarrow 3.7-4.2\, GHz$
$\therefore$ A-II, B-I, C-IV, D-III

A

$1: 1$

B

$2: 3$

C

$2:5$

D

$1: 2$

Solution

$ kx = m \left( L _0+ x \right) \omega^2$
$ \Rightarrow 12.5 x =\frac{1}{5}\left( L _0+ x \right) 25 \Rightarrow 1.5 x = L _0 $
$ \Rightarrow \frac{ x }{ L _0}=\frac{2}{3}$

A

NOR

B

NAND

C

OR

D

AND

A

Scattering

B

Chromatic aberration

C

Spherical aberration

D

Polarisation

Solution

Based on fact.

A

$941\, nm$

B

$974 \,nm$

C

$99.3\, nm$

D

$94.1 \,nm$

Solution

$\frac{ hc }{\lambda}=\left[1-\frac{1}{16}\right](13.6\, eV )$
So, $\lambda=94.1 \,nm$

A

$1: 2 $

B

$1: 4$

C

$1: 3$

D

$1: 1$

Solution

Displacement $=\Sigma$ area $=16-8+16-8=16\, m$
Distance $=\Sigma \mid$ area $\mid=48\, m$
$\frac{\text { displacement }}{\text { Distance }}=\frac{1}{3}$

A

$88 \times 10^{-4} T$

B

$1232 \times 10^{-4} T$

C

$352 \times 10^{-4} T$

D

$176 \times 10^{-4} T$

Solution

$ B =\mu_0 nI $
$ =4 \pi \times 10^{-7} \times 70 \times 10^2 \times 2$
$ =56 \pi \times 10^{-4} T $
$ =176 \times 10^{-4} T$

A

Both A and R are correct but R is NOT the correct explanation of A

B

Both A and R are correct and R is the correct explanation of A

C

A is not correct but R is correct

D

A is correct but R is not correct

Solution

Concept based

A

$\left(-\frac{3}{2}, \frac{1}{2}, \frac{1}{2}\right)$

B

$\left(-\frac{3}{2},-\frac{1}{2}, \frac{1}{2}\right)$

C

$\left(\frac{3}{2}, \frac{1}{2},-\frac{1}{2}\right)$

D

$\left(\frac{3}{2},-\frac{1}{2}, \frac{1}{2}\right)$

Solution

$ {\left[ T ^{-1}\right]=\left[ L ^1\right]^{ a }\left[ M ^1 L ^{-3}\right]^{ b }\left[\frac{ MLT ^{-2}}{ L }\right]^{ c }}$
$ \Rightarrow T ^{-1}= M ^{ b + c } \cdot L ^{ a -3 b } \cdot T ^{-2 c }$
$ c =\frac{1}{2}, b =-\frac{1}{2}, a -3 b =0$
$a +\frac{3}{2}=0 \Rightarrow a =-\frac{3}{2}$

A

$E_0 B_0=\omega k$

B

$E _0= kB _{ 0}$

C

$kE _{ 0 }=\omega B _{ 0 }$

D

$\omega E _{ 0 }= kB _{ 0 }$

Solution

$C =\frac{\omega}{ k }=\frac{ E _0}{ B _0}$

A

$45 \, V$

B

$40 \, V$

C

$80 \, V$

D

$90\, V$

Solution

$ R _{\text {eq }}=\frac{400 \times 100}{500}+100$
$ =180 \Omega $
$ i =\frac{90}{180}=\frac{1}{2} A$
Reading $=\frac{1}{2} \times \frac{400}{500} \times 100 $
$ =40 \text { volt }$

A

$ \frac{1}{2} B ^2 L ^2 \omega $

B

$ \frac{1}{4} BL ^2 \omega$

C

$\frac{1}{2} BL ^2 \omega $

D

$ \frac{1}{4} B ^2 L \omega$

Solution

$ \int d \varepsilon=\int B(\omega x) d x $
$ \varepsilon=B \omega \int\limits_0^L x d x=\frac{B \omega L^2}{2}$

A

Both A and R are correct but R is NOT the correct explanation of A

B

Both A and R are correct and R is the correct explanation of A

C

A is not correct but R is correct

D

A is correct but R is not correct

Solution

$T \propto \frac{1}{\sqrt{ g }}$

A

$6 \times 10^6 km$

B

$3 \times 10^6 km$

C

$6 \times 10^7 km$

D

$3 \times 10^7 km$

Solution

$ T ^2 \propto R ^3 \Rightarrow\left(\frac{ T _1}{ T _2}\right)^2=\left(\frac{ R _1}{ R _2}\right)^3 $
$ \Rightarrow\left(\frac{1}{2.83}\right)^2=\left(\frac{1.5 \times 10^6}{ R _2}\right)^3 $
$ \Rightarrow R _2=\left[(2.83)^2 \times\left(1.5 \times 10^6\right)^3\right]^{1 / 3} $
$ =8^{1 / 3} \times 1.5 \times 10^6=3 \times 10^6 km $

A

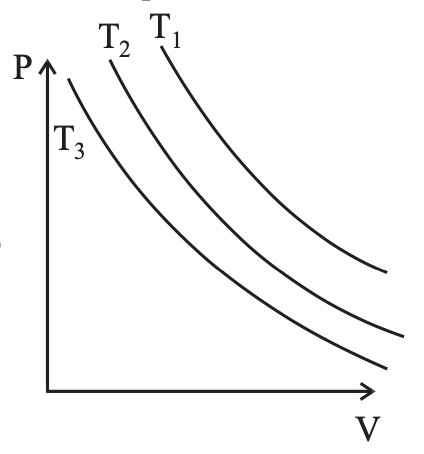
B

C

D

Solution

For isothermal process P-V graph is rectangular hyperbola

As dotted line is isobaric line which implies $T _3> T _2> T _1$ as volume is increasing.

A

$\lambda_\alpha>\lambda_p>\lambda_e$

B

$\lambda_\alpha<\lambda_p<\lambda_e$

C

$\lambda_\alpha=\lambda_p=\lambda_e$

D

$\lambda_\alpha>\lambda_p<\lambda_e$

Solution

$ \lambda_{ D }=\frac{ h }{ p }=\frac{ h }{\sqrt{2 mK }} $
$\therefore \lambda \propto \frac{1}{\sqrt{ m }} $
$ \because m _\alpha> m _{ p }> m _{ e }$
$ \lambda_{ c }>\lambda_{ p }>\lambda_\alpha$

Solution

As volume is constant,
So resistance $\propto$ (length $)^2$
$\Rightarrow \% \text { change in resistance }=20+20+\frac{400}{100}=44 \%$

Solution

After long time an inductor behaves as a resistance-less path.
So current through cell
$I =\frac{12}{ R / 3}=3 A \{\because R =12\, \Omega\}$

Solution

When the ball attain terminal velocity
$ F _{ v }=\left( mg - F _{ B }\right)(\because a =0) $
$ =\operatorname{V} \sigma_{ b } g - V \rho_{\ell} g $
$=\operatorname{Vg}\left(\sigma_{ b }-\rho_{\ell}\right) $
$=\frac{4}{3} \pi\left(10^{-3}\right)^3 \times 9.8(10.5-1.5) \times 10^3$
$ =3696 \times 10^{-7} N $
So , $x =7$

Solution

$ \vec{ F }=t \hat{ i }+3 t ^2 \hat{ j } $
$ \frac{ md \vec{ v }}{ dt }=t \hat{ i }+3 t ^2 \hat{ j } $
$ m =1 \,kg , \int\limits_0^{\vec{v}} dv =\int\limits_0^{ t } tdt \hat{ i }+\int\limits_0^{ t } 3 t ^2 dt \hat{ j } $
$ \vec{ v }=\frac{ t ^2}{2} \hat{ i }+ t ^3 \hat{ j } $
Power $=\vec{ F } \cdot \vec{ V }=\frac{ t ^3}{2}+3 t ^5$
At $ t =2$, power $=\frac{8}{2}+3 \times 32$
$ =100$

Solution

$ T =2 \pi \sqrt{\frac{ m }{ k }}=1$
$T ^{\prime}=2 \pi \sqrt{\frac{ m +3}{ k }}=2 $
$ \frac{ T }{ T ^{\prime}}=\sqrt{\frac{ m }{ m +3}}=\frac{1}{2}$
$ \Rightarrow \frac{ m }{ m +3}=\frac{1}{4} $
$ m =1$

Solution

No. of mole $=\frac{120}{240}=\frac{1}{2}$
No. of molecules $-\frac{1}{2} \times N _{ A }$
Energy released $=\frac{1}{2} \times 6 \times 10^{23} \times 200$
$=6 \times 10^{25} MeV$

Solution

$ I_1=\frac{m_1 R^2}{2} I_2=\frac{m_2(R / 2)^2}{2}$
$ \frac{I_1}{I_2}=\frac{4 m _1}{m_2}=\frac{4 \cdot \rho \pi R^2 \ell}{\rho \cdot \frac{\pi R^2}{4} \times \frac{\ell}{2}} \Rightarrow \frac{I_1}{I_2}=32$

Solution

Force on $5\, cm$ side is
$ |\vec{F}|=\text { ILB } \sin \theta $
$=(2)\left(5 \times 10^{-2}\right) \times \frac{3}{4} \times \frac{12}{13}=\frac{9}{130} N$
So, $x=9$

Solution

$ C _0=\frac{\in_0 A }{ d }=15 pF $
$ C =\frac{ K \in_0 A }{2 d }=\frac{3.5}{2} \times 15 pF =\frac{105}{4} pF $

Solution

$ \frac{ I }{ f _{ H _2 O }}=\left(\frac{\mu_{ g }}{\mu_{ H _2 O }}-1\right)\left(\frac{2}{ R }\right) $
$ =\frac{1}{8}\left(\frac{2}{ R }\right) $
$ =\frac{1}{\left(4 f _{ air }\right)}$
So, $f _{ H _2 O }=4 f _{\text {air }}=72\, cm$
So change in focal length $=72-18=54 \,cm$

A

$0,1,2,1$

B

$2,1,2,1$

C

$0,1,0,1$

D

$2,1,0,1$

Solution

$N _2$
$\sigma 1 s ^2 \sigma^* 1 s ^2 \sigma 2 s ^2 \sigma^* 2 s ^2 \pi 2 p _{ x }^2=\pi 2 p _{ y }^2 \frac{\sigma 2 p _{ z }^2}{ HOMO }$
$N _2^{+}-\sigma 1 s ^2 \sigma^* 1 s ^2 \sigma^* 2 s ^2 \sigma^* 2 s ^2 \pi 2 p _{ x }^2=\pi 2 p _{ y }^2 \frac{\sigma 2 p _{ z }^1}{ HOMO }$
$O _2-\sigma 1s ^2 \sigma^* 1 s ^2 \sigma 2 s ^2 \sigma^* 2 s ^2 \sigma 2 p _{ z }^2 $
$\pi 2 p _{ x }^2=\pi 2 p _{ y }^2$
$\pi^* 2 p _{ x }^1=\pi^* 2 p _{ y }^1( HOMO )$
$O _2^{+}-\sigma 1 s ^2 \sigma^* 1s ^2 \sigma 2 s ^2 \sigma ^* 2 s ^2 \sigma 2 p _{ z }^2 \pi 2 p _{ x }^2=\pi 2 p _{ y }^2 $
$\pi^* 2 p _{ x }^1=\pi^* 2 p _{ y }^0( HOMO )$
$ N _2 \Rightarrow 0$ unpaired $ e ^{-} \text {in HOMO }$
$ N _2^{+} \Rightarrow 1 $ unpaired $ e ^{-} \text {in HOMO } $
$ O _2 \Rightarrow 2 $ unpaired $ e ^{-} \text {in HOMO } $
$ O _2^{+} \Rightarrow 1 $ unpaired $e ^{-} \text {in HOMO }$

A

A is false but $R$ is true

B

Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$

C

$A$ is true but $R$ is false

D

Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$

Solution

Assertion - A : Benzene is more stable than cyclohexatriene (True)
Reason - R : Delocalised $\pi-$ e cloud lies B.M.O so more attracted by nuclei of carbon atom.
(True & Correct Explanation)

A

D only

B

C and D only

C

C only

D

A and B only

Solution

$Ce ^{+4}$ and $Tb ^{+4}$ act as oxidising agent.

A

Both a and c

B

a only

C

b only

D

c only

A

$PbS +4 H _2 O _2 \rightarrow PbSO _4+4 H _2 O$

B

$2 Fe ^{2+}+ H _2 O _2 \rightarrow 2 Fe ^{3+}+2 OH ^{-}$

C

$HOCl + H _2 O _2 \rightarrow H _3 O ^{+}+ Cl ^{-}+ O _2$

D

$Mn ^{2+}+ H _2 O _2 \rightarrow Mn ^{4+}+2 OH ^{-}$

A

8

B

12

C

9

D

10

Solution

$Z =55[ Cs ] \Rightarrow[ Xe ] 6 s ^1$
$\left[ Cs ^{+}\right] \Rightarrow[ Xe ]$ i.e. upto $5 s$ count $e ^{-}$of s-subshell
i.e. $1 s , 2 s , 3 s , 4 s , 5 s \Rightarrow 10$ electrons

A

Magnetic properties of transition metal complexes

B

The order of spectrochemical series

C

Colour of metal complexes

D

Stability of metal complexes

Solution

Crystal field theory introduce spectrochemical series based upon the experimental values of $\triangle$ but can't explain it's order. While other three points are explained by CFT. Specially when the CFSE increases thermodynamic stability of the complex increases.

A

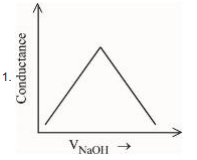
B

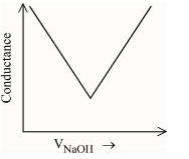
C

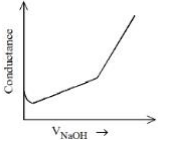
D

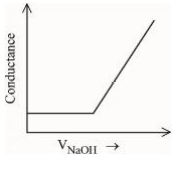
Solution

(A) $\rightarrow$ (B) Free $H ^{+}$ions are replaced by $Na ^{\oplus}$ which decreases conductance.
(B) $\rightarrow$ (C) Un-dissociated benzoic acid reacts with $NaOH$ and forms salt which increases ions & conductance increases.
(C) $\rightarrow$ (D) After equivalence point at (3), $NaOH$ added further increases $Na ^{\oplus} \& OH ^{\odot}$ ions which further increases the conductance.

A

C and E only

B

A and E only

C

A, B, D only

D

A, B and E only

Solution

(1) $Na > Cs > Li -$ true $\{$ If considered with sign $\}$ The low solubility of CsI is due to smaller hydration enthalpy of it's two ions $Li _2 CO _3$ is highly stable to heat - false In Conc. $NH _3, K$ formed blue solution - true All the alkali metal hydrides are ionic solid (True).

A

1

B

$0.5$

C

0 (zero)

D

2

Solution

$ t _{1 / 2} \propto\left( P _{ O }\right)^{1- n }$
$ \frac{\left( t _{1 / 2}\right)_1}{\left( t _{1 / 2}\right)_2}=\frac{\left( P _0\right)_1^{1- n }}{\left( P _{0_2}\right)_2^{1- n }} $
$\Rightarrow\left(\frac{4}{2}\right)-\left(\frac{50}{100}\right)^{1- n } $
$ \Rightarrow 2=\left(\frac{1}{2}\right)^{1- n } $
$ \Rightarrow 2=(2)^{ n -1} $
$ \Rightarrow n -1=1$
$n =2$

A

A-I, B-III, C-II, D-IV

B

A-II, B-I, C-III, D-IV

C

A-IV, B-III, C-II, D-I

D

A-I, B-II, C-III, D-IV

Solution

Theoretical, NCERT based

A

An average human being consumes equal amount of food and air

B

An average human being consumes more food than air

C

An average human being consumes nearly 15 times more air than food

D

An average human being consumes 100 times more air than food

Solution

Theoretical.

A

Blue

B

White

C

Red

D

Yellow

A

Statement I is true but Statement II is false

B

Statement I is false but Statement II is true

C

Both Statement I and Statement II are true

D

Both Statement I and Statement II are false

A

B

C

D

A

Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$

B

$A$ is not correct but $R$ is correct

C

Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$

D

$A$ is correct but $R$ is not correct

Solution

$Be$ has less negative value compared to other AEM. However it's reducing nature is due to large hydration energy associated with the small size of $Be ^{2+}$ ion and relatively large value of the atomization enthalpy of metal.

A

$sp ^3 d ^2$ and paramagnetic

B

$d ^2 sp ^3$ and paramagnetic

C

$d ^2 sp ^3$ and diamagnetic

D

$sp ^3 d ^2$ and diamagnetic

Solution

$\left[ Co \left( NH _3\right)_6\right]^{+3}- d ^2 sp ^3$, diamagnetic

A

Both Statement I and Statement II are correct

B

Statement I is incorrect but Statement II is correct

C

Both Statement I and Statement II are incorrect

D

Statement I is correct but Statement II is incorrect

Solution

Statement $-1$ is (True)
Pure aniline is colourless liquid
Statement - 2 is (False)
Aniline becomes dark brown due to action of air and light [oxidation]

A

Hydrogen sulphide

B

Sulphur dioxide

C

Carbon dioxide

D

Sulphur trioxide

Solution

$3 SO _2+ Cr _2 O _7^{2-}+2 H ^{+} \rightarrow 3 SO _4^{2-}+\underset{\text{green}}{2 Cr ^{+3}}+ H _2 O$

A

$Al$

B

$Cu$

C

$Ag$

D

$Fe$

Solution

$Ag$.
$4 Ag +8 CN ^{-}+ O _2+2 H _2 O \rightarrow 4\left[ Ag ( CN )_2\right]^{-}+4 OH ^{-} $
$ 2\left[ Ag ( CN )_2\right]^{-1}+ Zn \rightarrow 2 Ag \downarrow+\left[ Zn ( CN )_4\right]^{-2}$

Solution

For physisorptions
(a)Decreases with increase in temperature
(b)No appreciable activation energy is required

Solution

Let V.P. of pure $A$ be $P _{ A }^0$
Let V.P of pure $B$ be $P_B^0$
When $X _{ A }=0.7 \& X _{ B }=0.3$
$ P _{ s }=350$
$ \Rightarrow P _{ A }^0 \times 0.7+ P _{ B }^0 \times 0.3=350 ....$(i)
When $X _{ A }=0.2 \& X _{ B }=0.8$
$P _{ s }=410$
$ \Rightarrow P _{ A }^0 \times 0.2+ P _{ B }^0 \times 0.8=410,......$(ii)
Solving (i) and (ii)
$ P _{ A }^0=314 \,mm \,Hg $
$P _{ B }^0=434\, mm \,Hg $
$ =(314)$

Solution

No, of $\pi-$ bonds $=4$
Total $\pi-$ bonds $=8$

Solution

Mass percent, mole fraction, molarity, ppm, molality are used for measuring concentration terms.

Solution

The spectrum of Black body radiation is explained using quantization of energy. With increase in temperature, peak of spectrum shifts to shorter wavelength or higher frequency. For above graph $\rightarrow T _1> T _2> T _3> T _4$

Solution

At
(a) $\rightarrow CO _2$ exist as gas
(b) $\rightarrow$ liquefaction of $CO _2$ starts
(c) $\rightarrow$ liquefaction ends
(d) $\rightarrow CO _2$ exist as liquid.
Between (b) & (c) $\rightarrow$ liquid and gaseous $CO _2$ co-exist.
As volume changes from (b) to (c) gas decreases and liquid increases.
(A), (C) $\rightarrow$ correct

Solution

$ 1 \rightarrow 2 \Rightarrow $ Isobaric process
$ 2 \rightarrow 3 \Rightarrow $ Isochoric process
$ 3 \rightarrow 1 \Rightarrow $ Isothermal process
$W = W _{1 \rightarrow 2}+ W _{2 \rightarrow 3}+ W _{3 \rightarrow 1}$
$ =\left(- P \left( V _2- V _1\right)+0\left[- P _1 V _1 \ln \left(\frac{ V _2}{ V _1}\right)\right]\right) $
$ =\left[-1 \times(40-20)+0+\left[-1 \times 20 \ln \left(\frac{20}{40}\right)\right]\right] $
$ =-20+20 \ln 2$
$ =-20+20 \times 2.3 \times 0.3 $
$ =-6.2 \text { bar } L$
$| W |=6.2 \text { bar } 1=620\, J $

Solution

Total numbers of isomer $= 03$

Solution

No. of possible tripeptide :
Val & Pro is $2^3$
(1) val - val - val
(2)pro - pro - pro
(3) val - pro - pro
(4) pro - val - pro
(5) val - val - pro
(6) val - pro - val
(7)pro - pro - val
(8)pro - val - val

Solution

Concentration of calcium lactate $=0.005 \,M$,: concentration of lactate ion $=(2 \times 0.005)\, M$. Calcium lactate is a salt of weak acid $+$ strong base $\therefore$ Salt hydrolysis will take place.
$ pH =7+\frac{1}{2}( pKa +\log C ) $
$ =7+\frac{1}{2}(5+\log (2 \times 0.005))$
$ =7+\frac{1}{2}[5-2 \log 10]=7+\frac{1}{2} \times 3=8.5=85 \times 10^{-1}$

A

$-1$

B

1

C

3

D

5

Solution

Direction ratio of line $= \begin{vmatrix} \hat{ i } & \hat{ j } & \hat{ k } \\ 1 & 2 & 1 \\ 0 & 3 & -1\end{vmatrix} $
$ =\hat{ i }(-5)-\hat{ j }(-1)+\hat{ k }(3) $
$ =-5 \hat{ i }+\hat{ j }+3 \hat{ k }$

$ M (-5 \lambda+3, \lambda+2,3 \lambda+1) $
$ \overrightarrow{\operatorname{PM}} \perp(-5 \hat{ i }+\hat{ j }+3 \hat{ k }) $
$ -5(-5 \lambda+2)+(\lambda-7)+3(3 \lambda-6)=0 $
$ \Rightarrow 25 \lambda+\lambda+9 \lambda-10-7-18=0 $
$ \Rightarrow \lambda=1 $
Point $ M =(-2,3,4)=(\alpha, \beta, \gamma)$
$\alpha+\beta+\gamma=5$

A

4

B

3

C

2

D

0

Solution

$3\left(x^2+\frac{1}{x^2}\right)-2\left(x+\frac{1}{x}\right)+5=0$
$ 3\left[\left(x+\frac{1}{x}\right)^2-2\right]-2\left(x+\frac{1}{x}\right)+5=0$
Let $x +\frac{1}{ x }= t$
$ 3 t^2-2 t-1=0 $
$ 3 t^2-3 t+t-1=0$
$ 3 t(t-1)+1(t-1)=0 $
$( t -1)(3 t +1)=0 $
$ t =1,-\frac{1}{3}$
$ x +\frac{1}{ x }=1,-\frac{1}{3} \Rightarrow $ No solution.

A

9

B

11

C

7

D

6

Solution

Let $\vec{\beta}_1=\lambda \vec{\alpha}$
Now $\vec{\beta}_2=\vec{\beta}-\vec{\beta}_1$
$=(\hat{i}+2 \hat{ j }-4 \hat{ k })-\lambda(4 \hat{ i }+3 \hat{ j }+5 \hat{ k })$
$=(1-4 \lambda) \hat{ i }+(2-3 \lambda) \hat{ j }-(5 \lambda+4) \hat{ k }$
$ \vec{\beta}_2 \cdot \vec{\alpha}=0$
$\Rightarrow 4(1-4 \lambda)+3(2-3 \lambda)-5(5 \lambda+4)=0 $
$ \Rightarrow 4-16 \alpha+6-9 \lambda-25 \lambda-20=0$
$ \Rightarrow 50 \lambda=-10$
$\Rightarrow \lambda=\frac{-1}{5}$
$ \vec{\beta}_2=\left(1+\frac{4}{5}\right) \hat{ i }+\left(2+\frac{3}{5}\right) \hat{ j }-(-1+4) \hat{ k } $
$ \vec{\beta}_2=\frac{9}{5} \hat{ i }+\frac{13}{5} \hat{ j }-3 \hat{ k }$
$ 5 \vec{\beta}_2=9 \hat{ i }+13 \hat{ j }-15 \hat{ k }$
$5 \vec{\beta}_2 \cdot(\hat{ i }+\hat{ j }+\hat{ k })=9+13-15=7$

A

1011

B

2010

C

1010

D

2011

Solution

$f(x)=\frac{4^x}{4^x+2} $
$f(x)+f(1-x)=\frac{4^x}{4^x+2}+\frac{4^{1-x}}{4^{1-x}+2} $
$ =\frac{4^x}{4^x+2}+\frac{4}{4+2\left(4^x\right)}$
$ =\frac{4^x}{4^x+2}+\frac{2}{2+4^x}$
$ =1 $
$ \Rightarrow f(x)+f(1-x)=1$
Now $ f \left(\frac{1}{2023}\right)+ f \left(\frac{2}{2023}\right)+ f \left(\frac{3}{2023}\right)+\ldots \ldots+ $
$ \ldots \ldots \ldots+ f \left(1-\frac{3}{2023}\right)+ f \left(1-\frac{2}{2023}\right)+ f \left(1-\frac{1}{2023}\right)$
Now sum of terms equidistant from beginning and end is $1$
Sum $=1+1+1+\ldots \ldots \ldots .+1(1011$ times $)$
$=1011$

A

$-\frac{1}{2}(1-i \sqrt{3})$

B

$\frac{1}{2}(\sqrt{3}+i)$

C

$-\frac{1}{2}(\sqrt{3}-i)$

D

$\frac{1}{2}(1-i \sqrt{3})$

Solution

Let $\sin \frac{2 \pi}{9}+ i \cos \frac{2 \pi}{9}= z$
$ \left(\frac{1+ z }{1+\bar{z}}\right)^3=\left(\frac{1+ z }{1+\frac{1}{ z }}\right)^3= z ^3 $
$ \Rightarrow\left( i \left(\cos \frac{2 \pi}{9}- i \sin \frac{2 \pi}{9}\right)\right)^3$
$ =-i\left(\cos \frac{2 \pi}{3}- i \sin \frac{2 \pi}{3}\right)=-i\left(\frac{-1}{2}- i \frac{\sqrt{3}}{2}\right) $
$ \Rightarrow \frac{-1}{2}(\sqrt{3}-i) .$

A

$2 \pi$

B

$\frac{\pi}{6}$

C

$\frac{\pi}{3}$

D

$\frac{\pi}{2}$

Solution

$\int\limits_{\frac{3 \sqrt{2}}{4}}^{\frac{3 \sqrt{3}}{4}} \frac{48}{\sqrt{9-4 x^2}} d x$
We have $\int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+C$
Hence $\int\limits_{\frac{3 \sqrt{2}}{4}}^{\frac{3 \sqrt{3}}{4}} \frac{48}{\sqrt{9-4 x^2}} dx =\frac{48}{2} \times\left[\sin ^{-1} \frac{2 x}{3}\right]_{\frac{3 \sqrt{2}}{4}}^{\frac{3 \sqrt{3}}{4}}$
$=24 \times\left[\sin ^{-1}\left(\frac{2}{3} \times \frac{3 \sqrt{3}}{4}\right)-\sin ^{-1}\left(\frac{2}{3} \times \frac{3 \sqrt{2}}{4}\right)\right]$
$=24 \times\left[\sin ^{-1} \frac{\sqrt{3}}{2}-\sin ^{-1} \frac{1}{\sqrt{2}}\right]$
$ =24 \times\left(\frac{\pi}{3}-\frac{\pi}{4}\right)$
$ =24 \times \frac{\pi}{12}=2 \pi$

A

$e^2$

B

$\frac{3}{2} e^2$

C

$3 e^2$

D

$2 e ^2$

Solution

$ \left(x^2-3 y^2\right) d x+3 x y d y=0$
$\frac{d y}{d x}=\frac{3 y^2-x^2}{3 x y} \Rightarrow \frac{d y}{d x}=\frac{y}{x}-\frac{1}{3} \frac{x}{y}.....(1)$
Put $y=v x$
$\frac{d y}{d x}=v+x \frac{d v}{d x}$
(1) $\Rightarrow v+x \frac{d v}{d x}=v-\frac{1}{3} \frac{1}{v} $
$\Rightarrow v d v=\frac{-1}{3 x}$
Integrating both side
$ \frac{v^2}{2}=\frac{-1}{3} \ln x+c $
$\Rightarrow \frac{y^2}{2 x^2}=\frac{-1}{3} \ln x+c$
$ y(1)=1$
$\Rightarrow \frac{1}{2}=c$
$ \Rightarrow \frac{y^2}{2 x^2}=\frac{-1}{3} \ln x+\frac{1}{2} $
$ \Rightarrow y^2=-\frac{2}{3} x^2 \ln x+x^2$
$ y^2(e)=-\frac{2}{3} e^2+e^2=\frac{e^2}{3}$
$\Rightarrow 6 y ^2( e )=2 e ^2$

A

8

B

6

C

7

D

9

Solution

$ f ( x + y )= f ( x ) \cdot f ( y ) \forall x , y \in N , f (1)=3$
$ f (2)= f ^2(1)=3^2$
$ f (3)= f (1) f (2)=3^3$
$f (4)=3^4$
$f ( k )=3^{ k } $
$\displaystyle \sum_{ k =1}^{ n } f ( k )=3279$
$ f (1)+ f (2)+ f (3)+\ldots \ldots \ldots+ f ( k )=3279$
$ 3+3^2+3^3+\ldots \ldots \ldots 3^{ k }=3279$
$ \frac{3\left(3^{ k }-1\right)}{3-1}=3279 $
$ \frac{3^{ k }-1}{2}=1093$
$ 3^{ k }-1=2186 $
$ 3^{ k }=2187 $
$k =7$

A

$[-7.5,-6.5)$

B

$(-7.5,-6.5)$

C

$(-7.5,-6.5]$

D

$[-7.5,-6.5]$

Solution

$\displaystyle \lim _{x \rightarrow a}([x-5]-[2 x+2])=0$
$ \displaystyle\lim _{x \rightarrow a}([x]-5-[2 x]-2)=0$
$\displaystyle \lim _{x \rightarrow a}([x]-[2 x])=7 $
$ {[a]-[2 a]=7} $
$ a \in I, a=-7$
$ a \notin I, a=I+f $
Now, $[a]-[2 a]=7 $
$ -I-[2 f]=7$
Case-I: $ f \in\left(0, \frac{1}{2}\right)$
$ 2 f \in(0,1) $
$ - I =7 $
$ I =-7 \Rightarrow a \in(-7,-6.5) $
Case-II: $ f \in\left(\frac{1}{2}, 1\right)$
$ 2 f \in(1,2) $
$ - I -1=7$
$I =-8 \Rightarrow a \in(-7.5,-7)$
Hence, $a \in(-7.5,-6.5)$

A

$2 \sqrt{2}$

B

2

C

$\sqrt{6}$

D

4

Solution

$ AB :(\lambda+1) x +\lambda y =4$
$ AC : \lambda x +(1-\lambda) y +\lambda=0$
Vertex A is on $y$-axis
$\Rightarrow x=0$

So $y =\frac{4}{\lambda}, y =\frac{\lambda}{\lambda-1}$
$ \Rightarrow \frac{4}{\lambda}=\frac{\lambda}{\lambda-1} $
$ \Rightarrow \lambda=2$
$A B: 3 x+2 y=4$
$A C: 2 x-y+2=0$
$\Rightarrow A (0,2)$ Let $C (\alpha, 2 \alpha+2)$
Now (Slope of Altitude through C) $\left(-\frac{3}{2}\right)=-1$
$\left(\frac{2 \alpha}{\alpha-1}\right)\left(-\frac{3}{2}\right)=-1 \Rightarrow \alpha=-\frac{1}{2}$
So $C \left(-\frac{1}{2}, 1\right)$

Let Equation of tangent be $y = mx +\frac{3}{2 m }$
$ m^2+2 m-3=0 $
$ \Rightarrow m=1,-3$
So tangent which touches in first quadrant at $T$ is
$T \equiv\left(\frac{ a }{ m ^2}, \frac{2 a }{ m }\right) $
$ \equiv\left(\frac{3}{2}, 3\right)$
$ \Rightarrow CT =\sqrt{4+4}=2 \sqrt{2}$

A

$\frac{\pi}{2}$

B

$\frac{\pi}{4}$

C

$\frac{\pi}{6}$

D

$\frac{3 \pi}{4}$

Solution

In $\triangle CPB$

$ \cos \frac{\theta}{2}=\frac{P C}{2} \Rightarrow P C=2 \cos \frac{\theta}{2} $
$ \Rightarrow(h-4)^2+(k-5)^2=4 \cos ^2 \frac{\theta}{2} $
Now $(x-4)^2+(y-5)^2=\left(2 \cos \frac{\theta}{2}\right)^2$
$ \Rightarrow r_1=2 \cos \frac{\pi}{6}=\sqrt{3}$
$ r_2=2 \cos \frac{\theta_2}{2}$
$ r_3=2 \cos \frac{\pi}{3}=1 $
$ \Rightarrow r_1^2=r_2^2+r_3^2 $
$ \Rightarrow 3=4 \cos ^2 \frac{\theta_2}{2}+1 $
$ \Rightarrow 4 \cos ^2 \frac{\theta_2}{2}=2 $
$\Rightarrow \cos ^2 \frac{\theta_2}{2}=\frac{1}{2} $
$ \Rightarrow \theta_2=\frac{\pi}{2}$

A

$p \vee(p \wedge q)$

B

$(\sim p) \vee q$

C

$p \vee(p \wedge(\sim q))$

D

$p \vee((\sim p) \wedge q)$

Solution

$ \sim( p \wedge( p \rightarrow \sim q )) $
$ \equiv \sim p \vee \sim(\sim p \vee \sim q ) $
$ \equiv \sim p \vee( p \wedge q ) $
$ \equiv(\sim p \vee p ) \wedge(\sim p \vee q ) $
$ \equiv t \wedge(\sim p \vee q ) $
$ \equiv \sim p \vee q $

A

$2 f(0)-f(1)+f(3)=f(2)$

B

$f(3)-f(2)=f(1)$

C

$3 f(1)+f(2)=f(3)$

D

$f(1)+f(2)+f(3)=f(0)$

Solution

$f(x)=x^3-x^2 f^{\prime}(1)+x f^{\prime \prime}(2)-f^{\prime \prime \prime}(3), x \in R$
Let $f ^{\prime}(1)= a , f ^{\prime \prime}(2)= b , f ^{\prime \prime \prime}(3)= c$
$f ( x )=x^3- a x ^2+ b x - c $
$ f ^{\prime}(x)=3 x^2-2 a x+b$
$ f^{\prime \prime}(x)=6 x-2 a$
$ f^{\prime \prime \prime}(x)=6$
$c=6, a=3, b=6$
$ f(x)=x^3-3 x^2+6 x-6$
$ f(1)=-2, f(2)=2, f(3)=12, f(0)=-6$
$2 f(0)-f(1)+f(3)=2=f(2)$

A

$5 \sqrt{6}$

B

$2 \sqrt{6}$

C

$3 \sqrt{6}$

D

$4 \sqrt{6}$

Solution

Equation of plane passing through point of intersection of $P 1$ and $P 2$
$ P=P 1+k P 2 $
$ (x+(\lambda+4) y+z-1)+k(2 x+y+z-2)=0$
Passing through $(0,1,0)$ and $(1,0,1)$
$ (\lambda+4-1)+ k (1-2)=0 $
$ (\lambda+3)- k =0 .....$(1)
Also passing $(1,0,1)$
$ (1+1-1)+ k (2+1-2)=0 $
$ 1+ k =0 $
$k =-1$
put in (1)
$ \lambda+3+1=0 $
$ \lambda=-4$
Then point $(2 \lambda, \lambda,-\lambda)$
$ d =\left|\frac{-16-4,-4,4)}{\sqrt{6}}\right| $
$ d =\frac{18}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}=3 \sqrt{6}$

A

105

B

210

C

200

D

220

Solution

$ a_1+a_3=10=a_1+d \Rightarrow 5$
$ a _1+ a _2+a_3+ a _{ 4 }+ a _5+ a _6= 5 7 $
$ \Rightarrow \frac{6}{2}\left[a_1+a_6\right]=57 $
$ \Rightarrow a_1+a_6=19 $
$ \Rightarrow 2 a_1+5 d=19 \text { and } a_1+d=5$
$ \Rightarrow a_1=2, d=3$
Numbers : $2,5,8,11,14,17$
Variance $=\sigma^2=$ mean of squares-square of mean
$ =\frac{2^2+5^2+8^2+(11)^2+(14)^2+(17)^2}{6}-\left(\frac{19}{2}\right)^2$
$ =\frac{699}{6}-\frac{361}{4}=\frac{105}{4}$
$ 8 \sigma^2=210$

A

60

B

10

C

15

D

30

Solution

$S =0 \cdot\left({ }^{30} C _0\right)^2+1 \cdot\left({ }^{30} C _1\right)^2+2 \cdot \cdot\left({ }^{30} C _2\right)^2+\ldots \ldots+30 \cdot\left({ }^{30} C _{30}\right)^2 $
$S =30 .\left({ }^{30} C _0\right)^2+29 .\left({ }^{30} C _1\right)^2+28 .\left(^{30} C _2\right)^2+\ldots . .+0 .\left({ }^{30} C _0\right)^2$
$ 2 S =30 \cdot\left({ }^{30} C _0{ }^2++^{30} C _1^2+\ldots \ldots . \cdot{ }^{30} C _{30}{ }^2\right) $
$ S =15 \cdot{ }^{60} C _{30}=15 \cdot \frac{60 !}{(30 !)^2} $
$ \frac{15 \cdot 10 !}{(30 !)^2}=\frac{\alpha \cdot 60 !}{(30 !)^2}$
$\Rightarrow \alpha=15$

A

225

B

120

C

125

D

150

Solution

In each row and each column exactly one is to be placed -
$\therefore$ No. of such materials $=5 \times 4 \times 3 \times 2 \times 1=120$
Alternate :

Step-1 : Select any 1 place for 1 's in row 1. Automatically some column will get filled with 0 's.
Step-2 : From next now select 1 place for 1's. Automatically some column will get filled with 0 's. $\Rightarrow$ Each time one less place will be available for putting 1's.
Repeat step-2 till last row.
Req. ways $=5 \times 4 \times 3 \times 2 \times 1=120$

A

168

B

120

C

220

D

48

Solution

Four digit numbers greater than $7000$
$=2 \times 4 \times 3 \times 2=48$
Five digit number $=5 !=120$
Total number greater than $7000$
$=120+48=168$

A

1

B

$\sqrt{6}$

C

12

D

$2 \sqrt{3}$

Solution

Given $|\operatorname{adj}(\operatorname{adj}(\operatorname{adj} . A ))|=12^4$ $\Rightarrow| A |^{( n -1)^3}=12^4$
Given $n =3$
$\Rightarrow| A |^8=12^4 $
$\Rightarrow| A |^2=12$
$ | A |=2 \sqrt{3}$
We are asked
$ \left| A ^{-1} \cdot \operatorname{adj} A \right|$
$ =\left| A ^{-1}\right| \cdot|\operatorname{adj} A | $
$ =\frac{1}{| A |} \cdot| A |^{3-1} $
$ =| A |=2 \sqrt{3}$

A

$\left(\frac{72}{5},-\frac{21}{5}\right)$

B

$\left(\frac{72}{5}, \frac{21}{5}\right)$

C

$\left(-\frac{72}{5} \cdot-\frac{21}{5}\right)$

D

$\left(-\frac{72}{5}, \frac{21}{5}\right)$

Solution

$ x+2 y+3 z=3 ......$(i)
$ 4 x+3 y-4 z=4.......$(ii)
$ 8 x+4 y-\lambda z=9+\mu ......$(iii)
$ \text { (i) } \times 4 \text { - (ii) } \Rightarrow 5 y +16 z =8......$(iv)
(ii) $\times 2-$ (iii) $\Rightarrow 2 y+(\lambda-8) z=-1-\mu ......$(v)
(iv) $\times 2-$ (iii) $\times 5 \Rightarrow(32-5(\lambda-8)) z=16-5(-1-\mu)$
For infinite solutions $\Rightarrow 72-5 \lambda=0 \Rightarrow \lambda=\frac{72}{5}$
$21+5 \mu=0 \Rightarrow \mu=\frac{-21}{5}$
$\Rightarrow(\lambda, \mu) \equiv\left(\frac{72}{5}, \frac{-21}{5}\right)$

Solution

$ f(x)+\int\limits_0^x f(t) \sqrt{1-\left(\log _e f(t)\right)^2} d t=e$
$ \Rightarrow f(0)=e$
$ f^{\prime}(x)+f(x) \sqrt{1-(\ln f(x))^2}=0 $
$ f(x)=y $
$ \frac{d y}{d x}=-y \sqrt{1-(\ln y)^2}$
$ \int \frac{d y}{y \sqrt{1-(\ln y)^2}}=-\int d x $
Put $\ln y=t $
$ \int \frac{d t}{\sqrt{1-t^2}}=-x+C$
$ \sin ^{-1} t=-x+C \Rightarrow \sin ^{-1}(\ln y)=-x+C$
$ \sin ^{-1}(\ln f(x))=-x+C $
$ f(0)=e $
$ \Rightarrow \frac{\pi}{2}=C$
$ \Rightarrow \sin ^{-1}(\ln f(x))=-x+\frac{\pi}{2} $
$ \Rightarrow \sin ^{-1}\left(\ln f\left(\frac{\pi}{6}\right)\right)=\frac{-\pi}{6}+\frac{\pi}{2} $
$ \Rightarrow \sin ^{-1}\left(\ln f\left(\frac{\pi}{6}\right)\right)=\frac{\pi}{3} $
$ \Rightarrow \ln f\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}, $ we need $\left(6 \times \frac{\sqrt{3}}{2}\right)^2=27$

Solution

$ y^2-2 y=-x $
$ \Rightarrow y^2-2 y+1=-x+1 $
$ (y-1)^2=-(x-1) $
$y=-x$
Points of intersection
$x^2+2 x=-x$
$ x^2+3 x=0 $
$ x=0,-3$

$ A=\int\limits_0^3\left(-y^2+2 y+y\right) d y$
$ =\frac{3 y^2}{2}-\left.\frac{y^3}{3}\right|_0 ^3=\frac{9}{2} $
$8 A=36$

Solution

$ \vec{ a }=\hat{ i }+2 \hat{ j }+\lambda \hat{ k }, \vec{ b }=3 \hat{ i }-5 \hat{ j }-\lambda \hat{ k }, \vec{ a } \cdot \vec{ c }=7$
$ \vec{ a } \times \vec{ c }-\vec{ b } \times \vec{ c }=\vec{0}$
$ (\vec{ a }-\vec{ b }) \times \vec{ c }=0 \Rightarrow(\vec{ a }-\vec{ b }) \text { is paralleled to } \vec{ c }$
$ \vec{ a }-\vec{ b }=\mu \vec{ c } \text {, where } \mu \text { is a scalar } $
$ -2 \hat{ i }+7 \hat{ j }+2 \lambda \hat{ k }=\mu \cdot \overrightarrow{ c }$
Now $\vec{ a } \cdot \vec{ c }=7$ gives $2 \lambda^2+12=7 \mu$
And $\vec{b} \cdot \vec{c}=-\frac{43}{2}$ gives $4 \lambda^2+82=43 \mu$
$\mu=2$ and $\lambda^2=1$
$|\vec{ a } \cdot \vec{ b }|=8$

Solution

Given $R=\{(a, b),(b, c),(b, d)\}$
In order to make it equivalence relation as per given set, $R$ must be
$\{(a, a),(b, b),(c, c),(d, d),(a, b),(b, a),(b, c),(c, b)$,
$(b, d),(d, b),(a, c),(a, d),(c, d),(d, c),(c, a),(d, a)\}$
There already given so 13 more to be added.

Solution

Assume $B (\alpha,-2 \alpha) $ and $C (\beta+3, \beta)$
$\frac{\alpha+\beta+3+1}{3}=2 \text { also } \frac{-2 \alpha-2+\beta}{3}= a$
$ \Rightarrow \alpha+\beta=2\,\,\, -2 \alpha-2+\beta=3 a$
$ \Rightarrow \beta=2-\alpha \,\,\,\,-2 \alpha-\not 22 \not \not 2-\alpha=3 a \Rightarrow \alpha=- a$
Now both $B$ and $C$ lies as given line
$ \alpha- p \cdot 2 \alpha=21 a$
$ \alpha(1-2 p )=21 a....$(1)
$ -\alpha(1-2 p )=21 a \Rightarrow p =11 $
$\beta+3+ p \beta=21 a$
$ \beta+3+11 \beta=21 a $
$ 21 \alpha+12 \beta+3=0$
Also $\beta=2-\alpha$
$21 \alpha+12(2-\alpha)+3=0$
$ 21 \alpha+24-12 \alpha+3=0 $
$9 \alpha+27=0$
$ \alpha=-3, \beta=5$
So $BC =\sqrt{122}$ and $( BC )^2=122$

Solution

Given Binomial $\left( x -\frac{3}{ x ^2}\right)^{ n }, x \neq 0, n \in N$,
Sum of coefficients of first three terms
$ { }^{ n } C _0-{ }^{ n } C _1 \cdot 3+{ }^{ n } C _2 3^2=376$
$ \Rightarrow 3 n ^2-5 n -250=0 $
$\Rightarrow( n -10)(3 n +25)=0 $
$ \Rightarrow n =10$
Now general term ${ }^{10} C _{ r } x ^{10- r }\left(\frac{-3}{ x ^2}\right)^{ r }$
$ ={ }^{10} C _{ r } x ^{10- r }(-3)^{ r } \cdot x ^{-2 r }$
$ ={ }^{10} C _{ r }(-3)^{ r } \cdot x ^{10-3 r }$
Coefficient of $x ^4 \Rightarrow 10-3 r =4$
$\Rightarrow r =2 $
$ { }^{10} C _2(-3)^2=405$

Solution

$ P \left(\frac{ C }{ R }\right)=\frac{ P ( C ) P \left(\frac{ R }{ C }\right)}{ P ( A ) P \left(\frac{ R }{ A }\right)+ P ( B ) P \left(\frac{ R }{ B }\right)+ P ( C ) P \left(\frac{ R }{ C }\right)} $
$0.4=\frac{\frac{1}{3} \times \frac{\lambda}{(\lambda+4)}}{\frac{1}{3} \times \frac{4}{10}+\frac{1}{3} \times \frac{5}{10}+\frac{1}{3} \frac{\lambda}{(\lambda+4)}} $
$ \Rightarrow \lambda=6$

$\tan 30^{\circ}=3 t=\frac{3}{2} t^2$
$ \frac{1}{\sqrt{3}}=\frac{2}{t} $
$ t=2 \sqrt{3}$
$ \left(\frac{3}{2} t ^2, 3 t \right)=(18,6 \sqrt{3}) $
$ \ell^2=18^2+(6 \sqrt{3})^2 $
$ =324+108$
$ =432$

Solution

Shortest distance between the lines
$\frac{x+\sqrt{6}}{2}=\frac{y-\sqrt{6}}{3}=\frac{z-\sqrt{6}}{4}$
$\frac{x-\lambda}{3}=\frac{y-2 \sqrt{6}}{4}=\frac{2+2 \sqrt{6}}{5}$ is 6
Vector along line of shortest distance
$= \begin{vmatrix} i & j & k \\ 2 & 3 & 4 \\ 3 & 4 & 5\end{vmatrix}$, $\Rightarrow-\hat{ i }+2 \hat{ j }- k$ (its magnitude is $\sqrt{6}$ )
Now $\frac{1}{\sqrt{6}} \begin{vmatrix}\sqrt{6}+\lambda & \sqrt{6} & -3 \sqrt{6} \\ 2 & 3 & 4 \\ 3 & 4 & 5\end{vmatrix}=\pm 6$
$\Rightarrow \lambda=-2 \sqrt{6}, 10 \sqrt{6}$
So, square of sum of these values is $384$ .

Solution

$ 1^3+2^3+3^3 \ldots . \cdot+ n ^3=\left(\frac{ n ( n +1)}{2}\right)^2 $
$ 1 \cdot 3+2 \cdot 5+3 \cdot 7+\ldots \ldots+ n \text { terms }= $
$\displaystyle \sum_{ r =1}^{ n } r (2 r +1)=\displaystyle\sum_{ r =1}^{ n }\left(2 r ^2+ r \right)$
$ =\frac{2 \cdot n ( n +1)(2 n +1)}{6}+\frac{ n ( n +1)}{2}$
$ =\frac{ n ( n +1)}{6}(2(2 n +1)+3)$
$ =\frac{ n ( n +1)}{2} \times \frac{(4 n +5)}{3}$
$ =\frac{\frac{ n ^2( n +1)^2}{4}}{\frac{ n ( n +1)}{2} \times \frac{(4 n +5)}{3}}=\frac{9}{5} $
$\Rightarrow \frac{5 n ( n +1)}{2}=\frac{9(4 n +5)}{3}$
$ \Rightarrow 15 n ( n +1)=18(4 n +5) $
$ \Rightarrow 15 n ^2+15 n =72 n +90 $
$\Rightarrow 15 n ^2-57 n -90=0 \Rightarrow 5 n ^2-19 n -30=0 $
$ \Rightarrow( n -5)(5 n +6)=0$
$ \Rightarrow n =\frac{-6}{5} \text { or } 5$
$\Rightarrow n =5 \text {. } $

Solution

$\tan (\pi \cos \theta)+\tan (\pi \sin \theta)=0$
$ \tan (\pi \cos \theta)=-\tan (\pi \sin \theta) $
$ \tan (\pi \cos \theta)=\tan (-\pi \sin \theta)$
$ \pi \cos \theta= n \pi-\pi \sin \theta $
$ \sin \theta+\cos \theta= n \text { where } n \in I$
possible values are $n =0,1$ and $-1$ because
$-\sqrt{2} \leq \sin \theta+\cos \theta \leq \sqrt{2}$
Now it gives $\theta \in\left\{0, \frac{\pi}{2}, \frac{3 \pi}{4}, \frac{7 \pi}{4}, \frac{3 \pi}{2}, \pi\right\}$
So $\displaystyle\sum_{\theta \in S} \sin ^2\left(\theta+\frac{\pi}{4}\right)=2(0)+4\left(\frac{1}{2}\right)=2$