JEE Advanced Question Paper with Solution JEE Advanced 2020 Paper 2

A

$\sin \theta=\frac{ r }{ R }$

B

$\tan \theta=\frac{ r }{ R }$

C

$\sin \theta=\frac{ r }{2 R }$

D

$\cos \theta=\frac{ r }{2 R }$

Solution

At the verge of toppling, $N _{1}=0$
$mg \sin \theta h = mg \cos \theta r$ and $\cos \theta=\frac{ h }{ R }$
So, $m g \sin \theta h=m g \frac{h}{R} r$
$\Rightarrow \sin \theta= r / R$

A

rotate in the direction opposite to the direction of magnet’s motion

B

rotate in the same direction as the direction of magnet’s motion

C

not rotate and its temperature will remain unchanged

D

not rotate but its temperature will slowly rise

Solution

$\otimes$ is decreasing, so clockwise current in the square loop is induced.
So force (along the arrow) is acting on the disc.
So movement of disc is along the direction of motion of magnet.

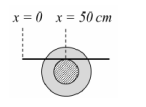
A

B

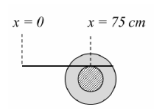
C

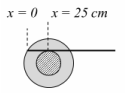
D

Solution

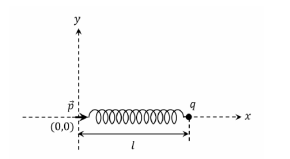
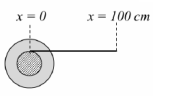
$v -\omega R =0$
$v_{p}=v+\omega r=v+\frac{v}{R} r=v\left(1+\frac{r}{R}\right)$
So, $\Delta x _{ p }=50\left(1+\frac{5}{10}\right)=75 \,cm$

A

$\frac{\pi}{2} NQB _{0} R ^{2}$

B

$\pi NQB _{0} R ^{2}$

C

$2 \pi NQB _{0} R ^{2}$

D

$4 \pi NQB _{0} R ^{2}$

Solution

A.M. $=\int \tau dt =\int N I \pi R ^{2} Bdt = N \pi R ^{2} B _{0} Q$

A

B

C

D

A

$\frac{15}{14}$

B

$\frac{35}{33}$

C

$\frac{7}{6}$

D

$\frac{5}{4}$

Solution

$800 \times 0.1+1000 \times x=1000 \times(0.58-x)$
$2000 \,x=500$
$x=0.25 \,m$
So, $h_{1}=0.35\, m , h_{2}=0.33 \,m$
$\frac{h_{1}}{h_{2}}=\frac{35}{33}$

A

$R \propto n ^{1 / 3}$ and $v \propto n ^{2 / 3}$

B

$R \propto n ^{2 / 3}$ and $v \propto n ^{1 / 3}$

C

$E=\frac{3}{2}\left(\frac{n^{2} h^{2} F^{2}}{4 \pi^{2} m}\right)^{1 / 3}$

D

$E=2\left(\frac{n^{2} h^{2} F^{2}}{4 \pi^{2} m}\right)^{1 / 3}$

Solution

$ F =-\frac{ dV }{ dr } $
$\frac{ mv ^{2}}{ R }= F $
$ mvr =\frac{ nh }{2 \pi}$
Solving above equations
$ R ^{3}=\frac{ n ^{2} h ^{2}}{4 \pi^{2} m } $
$v \propto n ^{1 / 3}$

A

power radiated by the filament is in the range $642\, W$ to $645\, W$

B

radiated power entering into one eye of the observer is in the range $3.15 \times 10^{-8} \, W$ to $3.25 \times 10^{-8}\, W$

C

the wavelength corresponding to the maximum intensity of light is $1160 \, nm$

D

taking the average wavelength of emitted radiation to be $1740\, nm$, the total number of photons entering per second into one eye of the observer is in the range $2.75 \times 10^{11}$ to $2.85 \times 10^{11}$

Solution

$ P = A \sigma T ^{4}$
$=64 \times 10^{-6} \times 5.67 \times 10^{-8} \times(2500)^{4} \approx 140\, W$
Power entering in eye
$=\frac{140}{4 \pi(100)^{2}} \pi\left(3 \times 10^{-3}\right)^{2}$
$=\frac{140 \times 9 \times 10^{-10}}{4}$
$=3.15 \times 10^{-8} W$
$\lambda T=b \Rightarrow \lambda=\frac{2.93 \times 10^{-6}}{2500}$
$\Rightarrow \lambda=1160$
Photons
$n \frac{12420}{1740}=\frac{3.15 \times 10^{-8}}{1.6 \times 10^{-19}}$
$=2.75 \times 10^{11}$

A

$\alpha+ p =2 \beta$

B

$p + q - r =\beta$

C

$p - q + r =\alpha$

D

$p + q + r =\beta$

Solution

$r=x^{\alpha} $
$v=x^{\beta} $
$a=x^{p} $
$P=x^{q} $
$F=x^{r}$
(A) $ra \rightarrow\left[ x ^{\alpha+ P }\right]$
$\left[\frac{\text { Energy }}{\text { mass }}\right]=[2 \beta]$
(B) $\left[\frac{ aP }{ F }\right]=[ at ]=[ v ]=\beta$
$P + q - r =\beta$

A

the particle will hit $T$ if projected at an angle $45^{\circ}$ from the horizontal

B

the particle will hit $T$ if projected either at an angle $30^{\circ}$ or $60^{\circ}$ from the horizontal

C

time taken by the particle to hit T could be $\sqrt{\frac{5}{6}} \mu s$ as well as $\sqrt{\frac{5}{2}} \mu s$

D

time taken by the particle to hit $T$ is $\sqrt{\frac{5}{3}} \mu s$

Solution

Range $= R =\frac{2 u \sin \theta}{ g _{\text {eff }}} u \cos \theta=5 \,m$
$\sin 2 \theta=\left(\frac{q E R}{m u^{2}}\right)=\frac{\sqrt{3}}{2}$
$\theta=30^{\circ}$
So for same range angle of projection is either $30^{\circ}$ or $60^{\circ}$
So Option (B) is correct
$T =\frac{2 u \sin \theta}{ g _{\text {eff }}}=\left(\sqrt{\frac{10}{3}} \times 10^{-6}\right) \sin \theta$
$ T _{1}\left(\theta=30^{\circ}\right)=\sqrt{\frac{5}{6}} \mu s $
$T _{2}\left(\theta=60^{\circ}\right)=\sqrt{\frac{5}{2}} \mu s$
So, Option (C) is correct

A

$I=\frac{v_{0} t}{\pi \rho} \ln \left(\frac{R_{2}}{R_{1}}\right)$

B

the outer surface is at a higher voltage than the inner surface

C

the outer surface is at a lower voltage than the inner surface

D

$\Delta V \propto I ^{2}$

Solution

Area of the strip $=( t$.dr $)$
$dR =\rho\left(\frac{\pi r }{ tdr }\right) $
$\sum \frac{1}{ dR }=\int\limits_{ R _{1}}^{ R _{2}} \frac{ tdr }{\pi \rho r } $
$\frac{1}{ R _{ eq }}=\left(\frac{ t }{\pi \rho}\right) L _{ n }\left(\frac{ R _{2}}{ R _{1}}\right) $
$ R _{ eq }=\frac{\pi \rho}{ t \times \ell n \left(\frac{ R _{2}}{ R _{1}}\right)}$
So, $I=\frac{V_{0}}{R_{\text {eq }}}=\left(\frac{V_{0} t}{\pi \rho}\right) \ln \left(\frac{R_{2}}{R_{1}}\right)$
So, option (A) is correct.

Electrons are revolving in a circular path so there is a centripetal force on the electron, which provide a transverse electric field.
The direction of transverse electric field is radially out side hence inner surface is at higher potential.
So, option (C) is correct.

Current density $J ( r )=\frac{ dl }{( tdr )}$
$J(r)=\frac{V_{0}}{(d r)({tdr})} $
$J(r)=\frac{V_{0}}{\left(\frac{\rho \pi r}{t d r}\right)({tdr})} $
$J(r)=\frac{V_{0}}{(\rho \pi r)}$
$I=n e A V_{d} $
$J(r)=n e V_{d} $
$\Rightarrow V_{d}=\left(\frac{J(r)}{n e}\right)=\left(\frac{V_{0}}{\rho \pi r n e}\right)$ ....(i)
Centripetal force
$eE _{ T }=\frac{ m _{ e } v _{ d }^{2}}{ r }$ ... (ii)
From (i) and (ii) $E_{T} \propto V_{0}^{2} \ldots$ (iii)
$\Delta V=\int E_{T} d r$
$\Rightarrow \Delta V \propto E _{ T }$ .... (iv)
From (iii) and (iv)
$\Delta V \propto V _{0}^{2}$
$l \propto V _{0}$
Hence
$\Delta V \propto l ^{2}$
Hence Option (D) is correct.

A

the force causing the molecules to move across the tube is $\Delta n k_{B} T S$

B

force balance implies $n_{l} \beta v l=\Delta n k_{B} T$

C

total number of molecules going across the tube per $\sec$ is $\left(\frac{\Delta n}{l}\right)\left(\frac{k_{B} t}{\beta}\right) S$

D

rate of molecules getting transferred through the tube does not change with time

Solution

$PV = NKT$
$P _{1}= n _{1} K _{ B } T$
$P _{2}= n _{2} K _{ B } T$
$n _{1}, n _{2} \rightarrow$ no. of molecules per unit volume
Force acting on the molecules
$F =\Delta PS$
$=\left( P _{1}- P _{2}\right) S$
$F =\left( n _{1}- n _{2}\right) K _{ B } TS =\Delta nk _{ B } TS \ldots$..(i)
So Option (A) is correct
Total no. of molecules in the tube $=\left( n _{1} S \ell\right)$
Force acting on each molecules
$F =-\beta v$
So total force acting on ( $n _{1} S \ell$ ) molecules $=-$
$(\beta v)( n _{1} s \ell$ )...(ii)
From (i) and (ii)
$\Delta nK _{ B } TS =(\beta v )\left( n _{1} S \ell\right)$
So, $\Delta nK _{ B } T =\left(\beta vn _{1} \ell\right) \ldots$ (iii)
So, Option (B) is correct.
No. of molecules going across the tube per second
$=\left({svn}_{1}\right)$
$=\left( sn _{1}\right)\left(\frac{\Delta nK _{\beta} T }{\beta n _{1} \ell}\right)=\left(\frac{ S \Delta n K _{\beta} T }{\beta \ell}\right)$
So, Option (C) is correct.
With respect to time $\Delta$ changes hence rate of molecules getting transferred through the tube changes with time.
So, Option (D) is incorrect.

Solution

Left finger will keep slipping till the kinetic friction is less than the static friction on right finger.
After that right finger will start slipping.
It will slip till the kinetic friction on it is less than static friction on the left one.
$N_{L} x=N_{R} \times 0.4$
$N_{L}+N_{R}=M g $
$\Rightarrow N_{L}=\frac{M g \times 0.4}{x+0.4} $ and $N_{R}=\frac{M g x}{x+0.4}$
$\mu_{k} N_{L} \geq \mu_{5} N_{R}$
$\frac{0.32 \times M g \times 0.4}{x+0.4} \geq \frac{0.4 \times M g x}{x+0.4} $
$x=\frac{0.4 \times 0.32}{0.4}=0.32 \,m$
Now right finger will start moving and it will stop, when kinetic friction on it will be more than static friction on left finger.
$N_{L} \times 0.32=N_{R} X_{R} $
$N_{L}+N_{R}=M g $
and $ \mu_{k} N_{R} \geq \mu_{g} N_{L}$
$0.32 \times \frac{M g \times 0.32}{X_{R}+0.32} \geq 0.4 \frac{M g \times X_{R}}{X_{R}+0.32}$
$X_{R}=\frac{0.32 \times 0.32}{0.4}=0.256\, m$
$=25.6 \,cm$

Solution

$\Rightarrow (S 2 R)=\left(\frac{0+\rho g h}{2}\right) h 2 R$
$4 S=\rho g h^{2}$
$h=\sqrt{\frac{4 S}{\rho g}}$
$h=\sqrt{\frac{2 \times 0.07}{10^{3} \times 10}}$
$=\sqrt{14} \times 10^{-3}=3.74$

Solution

Potential energy of a system after a small displacement.
$U=\frac{1}{2} k x^{2}+\frac{k^{\prime} p q}{(\ell+x)^{2}}$
$\frac{d U}{d x}=k x-\frac{2 k^{\prime} p q}{(\ell+x)^{3}} $
$\frac{d^{2} U}{d x^{2}}=k+\frac{6 k^{\prime} p q}{(\ell+x)^{4}}=k+3 k=4 k$
$f=\frac{1}{2 \pi} \sqrt{\frac{4 k}{m}}$
$f=\frac{1}{\pi} \sqrt{\frac{k}{m}}$
So, $ \delta=3.14$
and for angular frequency
$\omega =\frac{1}{\delta} \sqrt{\frac{ k }{ m }} $
$\delta =0.5$

Solution

$W_{\text {iso }}=R T \ln 4 $
$ T\left(4 V_{1}\right)^{2 / 3}=T^{\prime}\left(32 V_{1}\right)^{2 / 3} $
$\Rightarrow T^{\prime}=\frac{T}{4}$
$W_{\text {adia }}=\frac{2 R\left(T-\frac{T}{4}\right)}{3}=\left(\frac{9 R T}{8}\right)$
$\frac{W_{\text {iso }}}{W_{\text {adia }}}=\frac{8}{9} \ln 4=\frac{16}{9} \ln 2$
$\Rightarrow f=\frac{16}{9}=1.78$

Solution

$f=f_{0}\left(\frac{v}{v \mp u_{s}}\right)=f_{0}\left(1 \pm \frac{u_{s}}{v}\right)$
$f_{0}=\frac{v}{4 l_{0}} \& f=\frac{v}{4 l}$
$\frac{l-l_{0}}{l_{0}} \times 100=\left(\frac{f_{0}}{f}-1\right) \times 100$
$=\left(1 \mp \frac{u_{s}}{v}-1\right) \times 100$
$=\mp \frac{u_{s}}{v} \times-100$
$=\mp 0.62 \%$

Solution

$d Q=\left(\sigma_{0}\right)\left(1-\frac{x}{R}\right)(2 \pi x) d x$
$Q_{\frac{R}{4}}=\left(2 \pi \sigma_{0}\right) \int\limits_{0}^{R / 4}\left(x-\frac{x^{2}}{R}\right) d x$
$=\left(2 \pi \sigma_{0}\right)\left[\frac{5 R^{2}}{192}\right]$
$Q_{0}=\left(2 \pi \sigma_{0}\right) \int\limits_{0}^{R}\left(x-\frac{x^{2}}{R}\right) d x=(2 \pi \Delta) \frac{R^{2}}{6}$
$\phi=\frac{q_{\text {in }}}{\varepsilon_{0}}$
$ \Rightarrow \frac{\phi_{0}}{\phi}=\frac{1 \times 192}{(6) 5}=6.40$

A

$1: 1: 1$

B

$1: 1: 1.224$

C

$1: 1.128: 1.224$

D

$1: 1.128: 1$

Solution

Due to symmetrical graph given, the average value of velocity will be at the middle, which is also most probable velocity.
While calculating rms speed, we have to take average of square of speeds and its root. In square of speeds, higher speeds will give more contribution. So the value will be more than the average value.

A

$Pb _{3} O _{4}$

B

$KO _{2}$

C

$Na _{2} O _{2}$

D

$Li _{2} O _{2}$

Solution

$2 KO _{2}+2 H _{2} O \rightarrow 2 KOH + H _{2} O _{2}+ O _{2}$

A

$Ag$ and $Pb$

B

$Ag$ and $Cd$

C

$Cd$ and $Pb$

D

$Cd$ and $Zn$

Solution

$X=A g, Y=P b$

$\underset{(P)}{AgCl} + qa (NH_3) \rightarrow \underset{\text{Soluble}}{[Ag(NH_3)_2]^+}$ $\underset{(Q) \text{hot}}{PbCl_2} 6 KI \rightarrow \underset{\text{Yellow ppt }}{PbI_2}$

A

P and Q

B

Q and S

C

Q and R

D

R and S

Solution

$Q$ and $R$ represents identical molecules.

A

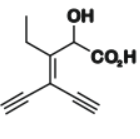
B

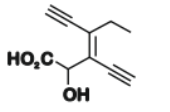
C

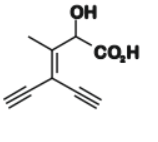
D

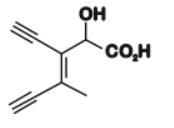
Solution

$3$-ethynyl-$2$-hydroxy-$4$-methylhex-$3$-en-$5$-ynoic acid

A

$P \rightarrow 2, Q \rightarrow 3, R \rightarrow 2, S \rightarrow 2$

B

$P \rightarrow 3, Q \rightarrow 1, R \rightarrow 1, S \rightarrow 2$

C

$P \rightarrow 2, Q \rightarrow 1, R \rightarrow 1, S \rightarrow 3$

D

$P \rightarrow 2, Q \rightarrow 3, R \rightarrow 3, S \rightarrow 1$

Solution

The Fischer projections of $P, Q, R$ and $S$ are

$P \rightarrow 2, Q \rightarrow 1, R \rightarrow 1, S \rightarrow 3$

A

System that satisfies the van der Waals equation of state

B

Process that is reversible and isothermal

C

Process that is reversible and adiabatic

D

Process that is irreversible and at constant pressure

Solution

The following expression of $P - V$ work done
$W=-\int P_{\text {ext }} d V$
is applicable for reversible isobaric as well as isothermal and adiabatic process. If $P_{\text {/ext }}$ is substituted for a Vander Waals equation then it becomes
$W=-\int\left(\frac{R T}{V-b}-\frac{a}{V^{2}}\right) d V$
But it is not applicable for irreversible process which are carried out very fast. So work done is calculated assuming final pressure remains constant throughout the process

A

The acidity of compound $I$ is due to delocalization in the conjugate base

B

The conjugate base of compound IV is aromatic

C

Compound II becomes more acidic, when it has a $- NO _{2}$ substituent

D

The acidity of compounds follows the order $| > | V > V > II > III $

Solution

Triphenylmethane $(I)$ is acidic because its conjugate base is stabilised by resonance.
Cyclopentadiene $(IV)$ is acidic because its conjugate base is aromatic.
Nitrobenzene is more acidic than benzene because nitro group is electron withdrawing. It will stabilise the conjugate base of benzene by - $I$ effect.
The correct order of acidity of the given compounds is $IV > V > I > II > III$.

A

B

C

D

A

$\left[ FeCl _{4}\right]^{-}$has tetrahedral geometry

B

$\left[ Co ( en )\left( NH _{3}\right)_{2} Cl _{2}\right]^{+}$has 2 geometrical isomers

C

$\left[ FeCl _{4}\right]^{-}$has higher spin-only magnetic moment than $\left[ Co ( en )\left( NH _{3}\right)_{2} Cl _{2}\right]^{-}$

D

The cobalt ion in $\left[ Co ( en )\left( NH _{3}\right)_{2} Cl _{2}\right]^{+}$has $s p^{3} d^{2}$ hybridization

Solution

$\left[ Co ( en )\left( NH _{3}\right)_{2} Cl _{2}\right]^{+}$ has $3$ geometrical isomers, one of them is optically active. So, it has $4$ stereoisomers.

I and II are enantiomers. $Co ^{+3}=3 d^{6}$
$d^{2} s p^{3}$ hybridization

A

The hypochlorite ion is the strongest conjugate base

B

The molecular shape of only chlorate ion is influenced by the lone pair of electrons of $Cl$

C

The hypochlorite and chlorate ions disproportionate to give rise to identical set of ions

D

The hypochlorite ion oxidizes the sulfite ion

Solution

$\underset{\text{most acidic}}{HClO_4} > HClO_3 > \underset{\text{least acidic}}{HOCl}$
Conjugate base
$\underset{\text{least basic}}{ClO_4^-} < ClO_3^- < \underset{\text{most basic}}{OCl^-}$
$CIO ^{-}+ SO _{3}^{-2} \rightarrow Cr ^{-}+ SO _{4}^{-2}$
$3 ClO ^{-} \rightarrow 2 Cr ^{-}+ ClO _{3}^{-}$
$4 ClO _{3}^{-} \rightarrow Cl ^{-}+3 ClO _{4}^{-}$

A

The empirical formula of the compound is $M X$

B

The cation $M$ and anion $X$ have different coordination geometries

C

The ratio of $M-X$ bond length to the cubic unit cell edge length is $0.866$

D

The ratio of the ionic radii of cation $M$ to anion $X$ is $0.414$

Solution

Contribution of $M=\frac{1}{2} \times 2=1$
Contribution of $X=\frac{1}{4} \times 4=1$
Formula $=M X$
Distance between $M$ and $X=\sqrt{\frac{a^{2}}{4}+\frac{a^{2}}{2}}$
$=\sqrt{\frac{3}{4}} a=\frac{\sqrt{3}}{2} a$
$=0.866 \,a$
Both cation and anion have same co-ordination number, i.e., $8$ .
Assuming, anions are in contact, the ratio of ionic radii of cation $M$ to anion $X$ is $0.732$, the minimum radius ratio for a cubical void.

Solution

No. of eq. of oxalic acid $=$ No. of eq. of $NaOH$
or $\frac{5.00 \times 0.10}{1000} \times 2=\frac{9.0 \times M}{1000} \times 1$
$\therefore $ Molarity of $NaOH$ solution $=\frac{1}{9}$
$=0.11 \,M$

Solution

$K _{1}$ at $1000\, K =\frac{10}{1}=10$
$K _{2}$ at $2000\, K =\frac{100}{1}=100$
$\Delta G _{1}^{\circ}=- RT _{1} \ln 10=-2.303\, RT _{1}$
$\Delta G _{2}^{\circ}=-2.303 \,RT _{2} \log 100$
$=-2 \times 2.303 \,RT _{2}$
$\frac{\Delta G _{1}^{\circ}}{\Delta G _{2}^{\circ}}=\frac{1 \times 1000}{2 \times 2000}=\frac{1}{4}=0.25$

Solution

$H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(l)$
$E_{\text {cell }}^{\circ}=1.23\, V$ (from given data)
$\because \Delta G^{\circ}=-n F E_{\text {cell }}^{\circ}$
$=-2 \times 96500 \times 1.23\, J / mol$
Work derived using $70 \%$ efficiency and on consumption of
$1.0 \times 10^{-3}$ mol of $H_{2}(g)$
$W=2 \times 96500 \times 1.23 \times 0.7 \times 1 \times 10^{-3}$
$=166.17\, J$
This work done $=$ Change in internal energy of monoatomic gas.
$\Rightarrow 166.17=n C_{v, m} \Delta T$
$\Rightarrow \Delta T=\frac{166.17 \times 2}{1 \times 3 R}$
$\Delta T=13.32\, K$

Solution

$H _{2} SO _{4}$ is limiting reagent
$\therefore $ Moles of $H _{2}( g )$ produced $=0.25$ moles
Using ideal gas equation : $PV = nRT$
$\Rightarrow V=\frac{0.25 \times 0.082 \times 300}{1}$
$V=6.15 \,L$

Solution

${ }_{92}^{238} U \rightarrow{ }_{82}^{206} Pb$
Number of a-particles emitted per nucleii of
${ }_{92}^{238} U=\frac{238-206}{4}=8$
Moles of ${ }_{92}^{238} U$ present initially $=\frac{68 \times 10^{-6}}{238}$
After three half lives, moles of ${ }_{92}^{238} U$ decayed $=\frac{7}{8} \times \frac{68 \times 10^{-6}}{238}$
$\therefore $ Number of alpha -particles emitted $=8 \times \frac{7}{8} \times \frac{68 \times 10^{-6}}{238} \times 6.02 \times 10^{23}$
$=12.04 \times 10^{17}$
$=1.2 \times 10^{18}$
$\therefore Z=1.2$

Solution

Degree of unsaturation $ = 18$

A

0

B

8000

C

8080

D

16000

Solution

Given $a+b=-20, a b=-2020, c+d=20, c d=2020-09-28$
$a^{2} c-a c^{2}+a^{2} d-a d^{2}+b^{2} c-b^{2} c-b c^{2}+b^{2} d-b d^{2}$
$=\left(a^{2}+b^{2}\right)(c+d)-(a+b)\left(c^{2}+d^{2}\right)$
$=\left((a+b)^{2}-2 a b\right)(c+d)-(a+b)\left((c+d)^{2}-2 c d\right)$
$=(400-2 \times 2020)(20)-(-20)(400-2 \times 2020)$
$=20 \times 800=16000$

A

$f$ is one-one, but NOT onto

B

$f$ is onto, but NOT one-one

C

$f$ is BOTH one-one and onto

D

$f$ is NEITHER one-one NOR onto

Solution

$f(x)$ is odd, continuous function
$f(x)= \begin{cases}x(x-\sin x) & , x \geq 0 \\ -x(x-\sin x) & , x < 0\end{cases}$
for $x \geq 0, f^{\prime}(x)=2 x-\sin x-x \cos x$
$=x(1-\cos x)+(x-\sin x) \geq 0$
for $x < 0, f(x)=-2 x+\sin x+x \cos x$
$=x(\cos x-1)-(x-\sin x)>0$ as $x < 0$
$\Rightarrow $ So $f(x)$ strictly increases in $(-\infty, \infty)$
$ \Rightarrow f(x)$ is one-one
$x \rightarrow \infty f ( x ) \rightarrow \infty$
$x \rightarrow-\infty f(x) \rightarrow-\infty$.
So $f(x)$ is onto

A

$(2-\sqrt{3})+\frac{1}{2}\left(e-e^{-1}\right)$

B

$(2+\sqrt{3})+\frac{1}{2}\left(e-e^{-1}\right)$

C

$(2-\sqrt{3})+\frac{1}{2}\left(e+e^{-1}\right)$

D

$(2+\sqrt{3})+\frac{1}{2}\left(e+e^{-1}\right)$

Solution

$\because f(x)=e^{x-1}-e^{-|x-1|}$
$\therefore f(x)=\begin{cases}0, & x<1 \\ e^{x-1}-e^{-(x-1)}, & x \geq 1\end{cases}$
and $g(x)=\frac{e^{x-1}+e^{1-x}}{2}$
$\therefore $ If $f(x)=g(x)$ then $2 e^{x-1}-2 e^{-(x-1)}$
$=e^{x-1}+e^{1-x}$
$\Rightarrow e^{x-1}=3 e^{1-x}$
$\Rightarrow e^{2(x-1)}=3$
$\therefore x=\frac{1}{2} \ln 3+1$

Required area $=\int\limits_{0}^{\frac{1}{2} \ln 3+1} g(x) d x-\int\limits_{1}^{\frac{1}{2} \ln 3+1} f(x) d x$
$=\frac{1}{2}\left(e^{x-1}-e^{1-x}\right)_{0}^{\frac{1}{2} \ln 3+1}-\left(e^{x-1}+e^{1-x}\right)_{1}^{\frac{1}{2} \ln 3+1}$
$=\frac{1}{2}\left(e^{\frac{1}{2} \ln 3}-e^{\frac{1}{2} \ln 3}\right)-\frac{1}{2}\left(e^{-1}-e\right)-\left(e^{\frac{1}{2} \ln 3}+e^{-\frac{1}{2} \ln 3}\right)+2$
$=(2-\sqrt{3})+\frac{1}{2}\left(e-\frac{1}{e}\right)$

A

$\frac{1}{\sqrt{2}}$

B

$\frac{1}{2}$

C

$\frac{1}{3}$

D

$\frac{2}{5}$

Solution

Equation of tangent to parabola $y^{2}=4 \lambda x$ at $P(\lambda, 2 \lambda)$ is :
$y \cdot 2 \lambda=2 \lambda(x+\lambda) $
$\therefore x-y+\lambda=0$
$\therefore $ Slope of tangent $=\frac{-b^{2}}{2 a^{2}}$
$\because 1 .\frac{-b^{2}}{2 a^{2}}=-1$
$\Rightarrow \frac{b^{2}}{a^{2}}=2$
$\therefore $ Eccentricity of ellipse $=\sqrt{1-\frac{a^{2}}{b^{2}}}$
$=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$
$\because$ Ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
passes through $(\lambda, 2 \lambda)$
Hence $b^{2}>a^{2}$

A

$\frac{40}{81}$

B

$\frac{20}{81}$

C

$\frac{1}{2}$

D

$\frac{1}{4}$

Solution

For $C_{1} P(h)=\frac{2}{3}$, for $C_{2} P(h)=\frac{1}{3}$,
given roots of the equation $x^{2}-\alpha x+\beta=0$ equal real roots

So required probability $=\left(\frac{2}{3}\right)^{2} \cdot{ }^{2} C_{1} \cdot \frac{1}{3} \cdot \frac{2}{3}+\left(\frac{1}{3}\right)^{2}\left(\frac{2}{3}\right)^{2}$
$=\frac{16}{81}+\frac{4}{81}=\frac{20}{81}$

A

$\frac{3 \pi}{2}$

B

$\pi$

C

$\frac{\pi}{2 \sqrt{3}}$

D

$\frac{\pi \sqrt{3}}{2}$

Solution

$P(x)=2\left(\frac{\pi}{2}-2 x\right)+4 \sin 2 x$
$=\pi-4 x+4 \sin 2 x$
$\frac{d P}{d x}=-4+8 \cos 2 x$
$\frac{d P}{d x}=0 \Rightarrow x=\frac{\pi}{6}$
$\frac{d^{2} P}{d x^{2}}=-16 \sin \frac{\pi}{3}<0$,
so local maxima exists at $x=\frac{\pi}{6}$
$\therefore $ Length of one side $=2 \sin 2 x=\sqrt{3}$
Length of other side $=\frac{\pi}{6}$
so area $=\sqrt{3} \frac{\pi}{6}=\frac{\pi}{2 \sqrt{3}}$

A

If $g$ is continuous at $x=1$, then $f g$ is differentiable at $x=1$

B

If $f g$ is differentiable at $x=1$, then $g$ is continuous at $x=1$

C

If $g$ is differentiable at $x=1$, then $f g$ is differentiable at $x=1$

D

If $f g$ is differentiable at $x=1$, then $g$ is differentiable at $x=1$

Solution

If $f g$ is differentiable at $x=1$, then
$\displaystyle\lim _{h \rightarrow 0} \frac{f g(1+h)-f g(1)}{h}$ exists finitely
$\Rightarrow \displaystyle\lim _{h \rightarrow 0} \frac{h\left[(1+h)^{2}+\sin (1+h) g(1+h)\right]-0}{h}$ exists finitely
$\Rightarrow \displaystyle\lim _{h \rightarrow 0}(1+\sin 1) g(1+h)$ exists finitely
So $\displaystyle\lim _{h \rightarrow 0^{-}} g(1+h)=\displaystyle\lim _{h \rightarrow 0^{-}} g(1+h) $
$\Rightarrow $ it does not mean that
$g(x)$ is continuous or differentiable at $x=1$
But if $g(x)$ is continuous or differentiable at $x=1$
then $\displaystyle\lim_{h \rightarrow 0^{-}} g(1+h)=\displaystyle\lim _{h \rightarrow 0^{-}} g(1+h)$,
hence $f g(x)$ will be differentiable

A

$M=I$

B

$\text{det} M=1$

C

$M^{2}=I$

D

$(\text{adj} M)^{2}=I$

Solution

$\because M^{-1}=\text{adj}(\text{adj} M)$
$\Rightarrow M^{-1}=|M| M \ldots(1)$
$\Rightarrow |M-1|=\left|M^{3}\right||M|$
$\Rightarrow |M|^{5}=1 \Rightarrow |M|=1$
Substituting $|M|=1$ in $(1)$ we get
$M=M^{-1} \Rightarrow M^{2}=1$
also adjM $=|M| \cdot M^{-1}=M$
Hence $(\text{adj} M)^{2}=M^{2}=I$

A

$\left|z+\frac{1}{2}\right| \leq \frac{1}{2}$ for all $z \in S$

B

$|z| \leq 2$ for all $z \in S$

C

$\left|z+\frac{1}{2}\right| \geq \frac{1}{2}$ for all $z \in S$

D

The set $S$ has exactly four elements

Solution

$\left|z^{2}+z+1\right|=1$
$\Rightarrow \left|\left(z+\frac{1}{2}\right)^{2}+\frac{3}{4}\right|=1$
$\Rightarrow \left(z+\frac{1}{2}\right)^{2}\left|-\frac{3}{4} \leq 1 \leq\right| z+\left.\frac{1}{2}\right|^{2}+\frac{3}{4}$
$\Rightarrow \frac{1}{4} \leq\left|z+\frac{1}{2}\right|^{2} \leq \frac{7}{4}$
$\Rightarrow \frac{1}{2} \leq\left|z+\frac{1}{2}\right| \leq \frac{\sqrt{7}}{2}$
option (c) is correct
$\because\left|z+\frac{1}{2}\right| \leq \frac{\sqrt{7}}{2}$
$\Rightarrow |z|-\frac{1}{2} \leq \frac{\sqrt{7}}{2}$
$ \Rightarrow |z| \leq \frac{\sqrt{7}+1}{2}$
$\Rightarrow |z| \leq 2$ option (B) is correct
Clearly $z=0,-1, i,-i,-1 \pm i$ a
re satisfying the given equation.
So we have more than $4$ solutions

A

$2 Y=X+Z$

B

$Y=X+Z$

C

$\tan \frac{X}{2}=\frac{x}{y+z}$

D

$x^{2}+z^{2}-y^{2}=x z$

Solution

$\because \tan \frac{x}{2}+\tan \frac{z}{2}=\frac{2 y}{x+y+z} $
let $x+y+z=2 s$
$\sqrt{\frac{(s-y)(s-z)}{s(s-x)}+\sqrt{\frac{(s-x)(s-y)}{s(s-z)}}}=\frac{y}{s}$
$\Rightarrow \sqrt{\frac{s-y}{s}\left(\frac{y}{\sqrt{(s-x)(s-z))}}\right)}=\frac{y}{s}$
$\Rightarrow \sqrt{\frac{s(s-y)}{(s-x)(s-z)}}=1$
$\Rightarrow \tan \frac{Y}{2}=1$
$\Rightarrow Y=\frac{\pi}{2}$

Clearly $Y=X+Z$
and $x^{2}+z^{2}=y^{2}$
Also, $\tan \frac{x}{2}=\sqrt{\frac{1-\cos x}{1+\cos x}}$
$=\sqrt{\frac{1-\frac{z}{y}}{1+\frac{z}{y}}}$
$=\sqrt{\frac{y-z}{y+z}}=\sqrt{\frac{y^{2}-z^{2}}{(y+z)^{2}}}$
$=\frac{x}{y+z}$

A

$\alpha-\gamma=3$

B

$l+m=2$

C

$\alpha-\gamma=1$

D

$l+m=0$

Solution

Clearly we can observe from the equations that $L_{1}$ and $L_{2}$ pass through $(1,0,1)$
Vectors in the directions of $L_{1}$ and $L_{2}$ are $(\hat{i}-\hat{j}+3 \hat{k})$ and $(-3 \hat{i}-\hat{j}+\hat{k})$ respectively which areequimodular and inclined at an acute angle, so their angle bisector will be along their resultant, which is $(-2 \hat{i}-2 \hat{j}+4 \hat{k})$. So equation of angle acute angle bisector will be
$\frac{x-1}{1}=\frac{y}{1}=\frac{z-1}{-2}($ Clearly $1=m=1)$
$\because$ Point $(\alpha, 1, \gamma)$ lies on this line, then $\alpha=2$ and $\gamma=-1$

A

$\int\limits_{0}^{1} x \cos x d x \geq \frac{3}{8}$

B

$\int\limits_{0}^{1} x \sin x d x \geq \frac{3}{10}$

C

$\int\limits_{0}^{1} x^{2} \cos x d x \geq \frac{1}{2}$

D

$\int\limits_{0}^{1} x^{2} \sin x d x \geq \frac{2}{9}$

Solution

We know that $\cos x=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\ldots$
So, $\cos x>1-\frac{x^{2}}{2}$ for all $x \in(0,1)$
$\Rightarrow x \cos x>x-\frac{x^{3}}{2}$
$\Rightarrow \int\limits_{0}^{1} x \cos x \,d x >\int\limits_{0}^{1}\left(x-\frac{x^{3}}{2}\right) d x$
$\Rightarrow \int\limits_{0}^{1} x \cos x\, d x>\frac{3}{8}($ Option $A$ is correct $)$ $\because x^{2} \cos x < x$ for all $x \in(0,1)$
$\Rightarrow \int\limits_{0}^{1} x^{2} \cos x \,d x < \int\limits_{0}^{1} x d x$
$\Rightarrow \int\limits_{0}^{1} x^{2} \cos x \,d x < \frac{1}{2}($ Option $C$ is incorrect $)$
Again we know that, $\sin x=x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\ldots$
So, $\sin x > x-\frac{x^{3}}{6}$ for all $x \in(0,1)$
$\Rightarrow x \sin x > x^{2}-\frac{x^{4}}{6}$
$\int\limits_{0}^{1} x \sin x d x>\int\limits_{0}^{1}\left(x^{2}-\frac{x^{4}}{6}\right) d x$
$\Rightarrow \int\limits_{0}^{1} x \sin d x>\frac{3}{10}$ (Option $B$ is correct) $\because x^{2} \sin x>x^{3}-\frac{x^{5}}{6}$
$\Rightarrow \int\limits_{0}^{1} x^{2} \sin x\, d x>\frac{2}{9}$ (Option $D$ is correct)

Solution

By AM-GM inequality
$\frac{3^{y_{1}}+3^{y_{2}}+3^{y_{3}}}{3} \geq\left(3^{y_{1}} \cdot 3^{y_{2}} \cdot 3^{y_{3}}\right)^{\frac{1}{3}}$
$\Rightarrow 3^{y_{1}}+3^{y_{2}}+3^{y_{3}} \geq 3\left(\frac{{y_{1}}+y_{2}+y_{3}}{3}\right)$
$\Rightarrow 3^{y_{1}}+3^{y_{2}}+3^{y_{3}} \geq 3^{4}$
$\Rightarrow \log 3\left(3^{y_{1}}+3^{y_{2}}+3^{y_{3}}\right) \geq 4$
$\Rightarrow m=4$ ,
Similarly
For $\log _{3} x_{1}+\log _{3} x_{2}+\log _{3} x_{3}=\log _{3}\left(x_{1} x_{2} x_{3}\right)=P($ say $)$
$x_{1}+x_{2}+x_{3} \geq 3\left(x_{1} x_{2} x_{3}\right)^{\frac{1}{3}}$
$3 \geq\left(x_{1} x_{2} x_{3}\right)^{\frac{1}{3}}$
$\therefore \log _{3} 3 \geq \frac{1}{3} \log \left(x_{1} x_{2} x_{3}\right)$
$\therefore 3 \geq P$
$\Rightarrow M=3$
$\therefore \log _{2} m^{3}+\log _{3} m^{2}=\log _{2} 4^{3}+\log _{3} 3^{2}$
$=6+2=8$

Solution

$\because 2\left(a_{1}+a_{2}+a_{n}\right)=b_{1}+b_{2}+\ldots+b_{n} $
$\Rightarrow n[2 c+(n-1) 2]=c\left(2^{n}-1\right) $
$\Rightarrow c\left(2^{n}-2 n-1\right)=2 n^{2}-2 n $
$\Rightarrow c=\frac{2 n^{2}-2 n}{2^{n}-2 n-1} $
$\because c \in N, 2 n^{2}-2 n \geq 2^{n}-2 n-1 $
$\Rightarrow 2 n^{2}+1 \geq 2^{n} $
$\Rightarrow n \leq 6 $
also $ c > 0 \Rightarrow n > 2$
So possible values of $n$ are $3,4,5$ and $6$
when $n=3, c=12$
$n=4, c=\frac{24}{7}$ (not possible)
$n=5, c=\frac{40}{21}$ (not possible)
$n=6, c=\frac{60}{51}$ (not possible)
So, there exists only one value of '$c$'.

Solution

Let $\pi x=\theta$
$f(x)=(3-\sin 2 \theta) \sin \left(\theta-\frac{\pi}{4}\right)-\sin \left(3 \theta+\frac{\pi}{4}\right)$
$=(3-\sin 2 \theta) \frac{(\sin \theta-\cos \theta)}{\sqrt{2}}-\left(\frac{\sin 3 \theta}{\sqrt{2}}+\frac{\cos 3 \theta}{\sqrt{2}}\right)$
$=\frac{1}{\sqrt{2}}\left[(3-\sin 2 \theta)(\sin \theta-\cos \theta)-\left(3 \sin \theta-3 \cos \theta-4 \sin ^{3} \theta+4 \cos ^{3} \theta\right)\right]$
$=\frac{1}{\sqrt{2}}[(3-\sin 2 \theta)(\sin \theta-\cos \theta)-\{3(\sin \theta-\cos \theta)-4(\sin \theta-\cos \theta)$
$\left.\left.\left(1+\frac{\sin 2 \theta}{2}\right)\right\}\right]$
$=\frac{(\sin \theta-\cos \theta)}{\sqrt{2}}(3-\sin 2 \theta+1+2 \sin 2 \theta)$
$\therefore $ For $f(x) \geq 0$

$\therefore [\alpha, \beta]=\left[\frac{1}{4}, \frac{5}{4}\right]$
$\Rightarrow [\beta-\alpha]=\frac{5}{4}-\frac{1}{4}=1$

Solution

Equation reduces to $(4 \vec{a}+3 \vec{b}) \cdot \vec{c}=7 \vec{a} \cdot \vec{b}$
But $\vec{a}+\vec{b}+\vec{c}=0$
So, $(4 \vec{a}+3 \vec{b}) \cdot(\vec{a}+\vec{b})=-7 \vec{a} \cdot \vec{b}$
$\vec{a} \cdot \vec{b}=-6$
$|\vec{a} \times \vec{b}|^{2}=108$

Solution

$f(x)=\left(x^{2}-1\right)^{2} \cdot p(x)$
where $p(x)=a_{0}+a_{1} x+a_{2} x^{2}+a_{3} x^{3}$
$\because f(x)$ has two repeated roots $x=1$ and $x=-1$
So $f^{\prime}(x)$ has at least 3 roots $x=1, x=-1$ and $x=c$
Where $c \in(-1,1)$, so $m_{f}=3$
Between any two distinct roots of $f^{\prime}(x)$ there will be at least one root of
$f^{\prime \prime}(x)$, so $m_{f^{\prime \prime}}=2$
$m_{f^{\prime}}+m_{f^{\prime \prime}}=5$

Solution

$\displaystyle\lim _{x \rightarrow 0^{+}} \frac{(1-x)^{1 / x}-\frac{1}{e}}{x^{a}}=\displaystyle\lim _{x \rightarrow 0^{+}} \frac{e^{\frac{\ln (1-x)}{x}}-\frac{1}{e}}{x^{a}}$
$=\displaystyle\lim _{x \rightarrow 0^{+}} \frac{1}{e} \frac{\left(e^{\frac{-x-\frac{x^{2}}{2}}{x}}-1\right)}{x^{a}}=\displaystyle\lim _{x \rightarrow 0} \frac{1}{e}\left(\frac{e^{-\frac{x}{2}}-1}{x^{a}}\right)$
For value of limit to be a non-zero real number $a =1$