JEE Advanced Question Paper with Solution JEE Advanced 2021 Paper 2

JEE Advanced Physics Question Paper with Solution JEE Advanced 2021 Paper 2

Q1. One end of a horizontal uniform beam of weight $W$ and length $L$ is hinged on a vertical wall at point $O$ and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point $Q$, at a height $L$ above the hinge at point $O$. A block of weight $\alpha W$ is attached at the point $P$ of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of $(2 \sqrt{2})$ W. Which of the following statement(s) is(are) correct?

A

The vertical component of reaction force at $O$ does not depend on $\alpha$

B

The horizontal component of reaction force at $O$ is equal to $W$ for $\alpha=0.5$

C

The tension in the rope is $2 \,W$ for $\alpha=0.5$

D

The rope breaks if $\alpha > 1.5$

Q2. A source, approaching with speed $u$ towards the open end of a stationary pipe of length $L$, is emitting a sound of frequency $f _{ s }$. The farther end of the pipe is closed. The speed of sound in air is $v$ and $f _{0}$ is the fundamental frequency of the pipe. For which of the following combination(s) of $u$ and $f_{s}$, will the sound reaching the pipe lead to a resonance?

A

$u =0.8 \,v$ and $f _{ s }= f _{0}$

B

$u=0.8\, v$ and $f _{ s }=2\, f _{0}$

C

$u =0.8 \,v$ and $f _{ s }=0.5\, f _{0}$

D

$u=0.5 \,v$ and $f _{ s }=1.5 \,f _{0}$

Solution

image
Natural frequency of closed pipe
$f =(2 n +1) f _{0}$
$f _{0}$ is fundamental frequency
$n =0,1,2, \ldots \ldots \ldots .$
frequency of source received by pipe
$f ^{\prime}= f _{ s }\left[\frac{ v -0}{ v - u }\right]$
For resonance $f ^{\prime}= f$
$f_{s}\left[\frac{v}{v-u}\right]=(2 n+1) f_{0}$
If $u=0.8 \,v\,\,\,\, f _{ s }= f _{0}$
$f ^{\prime}=\frac{ v }{0.2 \,v } f _{0}=5\, f _{0}$
for $n =2$ pipe can be in resonance
Hence, option (A) is correct.
If $u =0.8 \,v \,\,\, f _{ s }=2\, f _{0}$
$f ^{\prime}=\frac{ v }{0.2 v } \times 2\, f _{0}=10\, f _{0}$
If $u=0.8\, v ,\,\,\, f_{ S }=0.5\, f _{0}$
$f ^{\prime}=\frac{ v }{0.2\, v } \times 0.5\, f _{0}=2.5\, f _{0}$
Not possible
If $u=0.5\, v , \,\,\,f_{ S }=1.5\, f _{0}$
$f ^{\prime}=\frac{ v }{0.5\, v } \times 1.5\, f _{0}=3\, f _{0}$
for $n =1 \,\,\,f =3 \,f _{0}$
pipe can be in resonance
Hence, option (D) is correct.

Q3. For a prism of prism angle $\theta=60^{\circ}$, the refractive indices of the left half and the right half are, respectively, $n _{1}$ and $n _{2}\left( n _{2} \geq n _{1}\right)$ as shown in the figure. The angle of incidence $i$ is chosen such that the incident light rays will have minimum deviation if $n _{1}= n _{2}= n =1.5$. For the case of unequal refractive indices, $n _{1}= n$ and $n _{2}=$ $n +\Delta n$ (where $\Delta n << n$ ), the angle of emergence $e=i+\Delta e$. Which of the following statement(s) is(are) correct?

A

The value of $\Delta e$ (in radians) is greater than that of $\Delta n$

B

$\Delta e$ is proportional to $\Delta n$

C

$\Delta e$ lies between $2.0$ and $3.0$ milliradians, if $\Delta n =2.8 \times 10^{-3}$

D

$\Delta e$ lies between $1.0$ and $1.6$ milliradians, if $\Delta n =2.8 \times 10^{-3}$

Solution

image
Diagram at minimum deviation for $n _{1}= n _{2}= n$
$n =1.5$
$r_{1}=r_{2}=\theta / 2=30^{\circ}$
for face $AQ$
$n \sin r _{2}=\sin e$
$1.5 \sin 30^{\circ}=\frac{3}{2} \times \frac{1}{2}=\sin e$
$\sin e =\frac{3}{4}, \,\,\, \cos e =\frac{\sqrt{7}}{4}$
When $n _{2}$ is given small variation there will be no change in path of light ray inside prism.
As deviation on face $AC$ is zero.
So, $r_{2}=30^{\circ}$
Now for face $AQ$
$n _{2} \sin 30^{\circ}=\sin e$
for small change in $n _{2}$ change in $e$ is given by
$dn _{2} \sin 30^{\circ}=\cos\, e \,de$
or $dn _{2}=\Delta n\,\, de =\Delta e$
$\Delta n \sin 30^{\circ}=\cos e \Delta e$
$\Delta n \frac{1}{2}=\frac{\sqrt{7}}{4} \Delta e$
$\Delta n =\frac{\sqrt{7}}{2} \Delta e \ldots$ (i)
$\Delta n >\Delta e$
$\Delta n \propto \Delta e$
Hence, option (B) is correct.
$\Delta e =\frac{2.8 \times 10^{-3} \times 2}{\sqrt{7}}$
Hence, option (C) is correct.

Q4. A physical quantity $\vec{ S }$ is defined as $\vec{ S }=(\vec{ E } \times \vec{ B }) / \mu_{0}$, where $\vec{ E }$ is electric field, $\vec{ B }$ is magnetic field and $\mu_{0}$ is the permeability of free space. The dimensions of $\vec{ S }$ are the same as the dimensions of which of the following quantity(ies)?

A

$\frac{\text { Energy }}{\text { Charge } \times \text { Current }}$

B

$\frac{\text { Force }}{\text { Lenght } \times \text { Time }}$

C

$\frac{\text { Energy }}{\text { Volume }}$

D

$\frac{\text { Power }}{\text { Area }}$

Solution

$\vec{ S }=\vec{ E } \times \vec{ B }$
Method - 1:
$\vec{ S }$ is pointing vector which is defined as energy flowing per unit area in unit time.
S.I. unit of $S$ is Watt $/ m ^{2}$.
Method 2:
$\because B =\mu_{0} ni \Rightarrow \frac{1}{\mu_{0}}=\frac{ ni }{ B } $
$S =\frac{1}{\mu_{0}} EB \cos \theta = niE \cos \theta$
S.I. unit of $S =\frac{1}{\text { meter }} \times \frac{q}{\text { time }} \times \frac{\text { Force }}{q}$
$=\frac{\text { Force }}{\text { meter }-\text { time }}$

Q5. A heavy nucleus $N$, at rest, undergoes fission $N \rightarrow P + Q$, where $P$ and $Q$ are two lighter nuclei. Let $\delta= M _{ N }$ - $M_{P}-M_{Q}$, where $M_{P}, M_{Q}$ and $M_{N}$ are the masses of $P, Q$ and $N$, respectively. $E _{P}$ and $E_{Q}$ are the kinetic energies of $P$ and $Q$, respectively. The speeds of $P$ and $Q$ are $v_{P}$ and $v_{Q}$, respectively. If $c$ is the speed of light, which of the following statement(s) is(are) correct?

A

$E_{p}+E_{Q}=c^{2} \delta$

B

$E_{p}=\left(\frac{M_{p}}{M_{p}+M_{Q}}\right) c^{2} \delta$

C

$\frac{ v _{ P }}{ v _{ Q }}=\frac{ M _{ Q }}{ M _{ P }}$

D

The magnitude of momentum for $P$ as well as $Q$ is $c \sqrt{2 \mu \delta}$, where $\mu=\frac{ M _{ p } M _{ Q }}{\left( M _{ p }+ M _{ Q }\right)}$

Solution

Energy released during process
$Q =\delta c ^{2}$ .... (1)
$\because$ momentum is conserved in process.
$\Rightarrow 0= m _{ p } v _{ p }- m _{ Q } . v _{ Q }$
$\Rightarrow \frac{ v _{ P }}{ v _{ Q }}=\frac{ m _{ Q }}{ m _{ P }}$ ....(2)
$E _{ P }=\frac{1}{2} m _{ p } v _{ P }^{2}$
$E _{ Q }=\frac{1}{2} m _{ Q } v _{ Q }^{2}$
$\Rightarrow \frac{ E _{ p }}{ E _{ Q }}=\frac{ m _{ Q }}{ m _{ p }}$ .... (3)
Solving (1) and (3),
$E_{P}=\frac{m_{Q}}{m_{P}+m_{Q}} \delta c^{2}$
$E_{Q}=\frac{m_{p}}{m_{p}+m_{Q}} \delta c^{2}$
Momentum $P=\sqrt{2 m_{P} E_{p}}=\sqrt{2 m_{Q} E_{Q}}$
$=\sqrt{2 m _{ p } \frac{ m _{ Q }}{ m _{ p }+ m _{ Q }} \cdot \delta c ^{2}}= c \sqrt{\frac{2 m _{ p } m _{ Q }}{ m _{ p }+ m _{ Q }} \cdot \delta}$

Q6. Two concentric circular loops, one of radius $R$ and the other of radius $2 R$, lie in the $x y$-plane with the origin as their common centre, as shown in the figure. The smaller loop carries current $I_{1}$ in the anti-clockwise direction and the larger loop carries current $I_{2}$ in the clock wise direction, with $I_{2}>2 I_{1}, \vec{B}(x, y)$ denotes the magnetic field at a point $(x, y)$ in the $x y$-plane. Which of the following statement (s) is ( are ) correct?

A

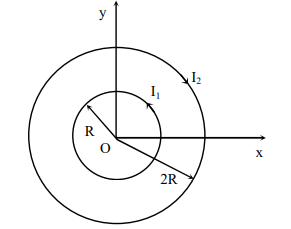
$\vec{ B }( x , y )$ is perpendicular to the $xy$-plane at any point in the plane

B

$|\vec{ B }( x , y )|$ depends on $x$ and $y$ only through the radial distance $r =\sqrt{ x ^{2}+ y ^{2}}$

C

$|\vec{ B }( x , y )|$ is non-zero at all points for $r < R$

D

$\vec{ B }( x , y )$ points normally outward from the $xy$-plane for all the points between the two loops

Solution

Consider a circular loop of radius $r$ in $x - y$ plane and having centre at origin
$\oint \vec{ B } \cdot \overrightarrow{ d \ell}=0$
$B \oint d \ell \cos \theta=0$
$\because B \neq 0 \,\,\,$ for given $r$
$\Rightarrow \cos \theta=0$
$\theta=90^{\circ}$
image
Here $d \ell$ is in $xy$ plane $\Rightarrow B$ is normal to plane (B can't be in $xy$ plane as its magnetic lines would have been in radial direction)
Also, for given $r , B$ must be same in magnitude for all points on loop of radius $r$.
At centre $B =\left(\frac{\mu_{0} i _{1}}{2 R }-\frac{\mu_{0} i _{2}}{4 R }\right)$
(inwards)
image
For point $P$, Let field of inner loop increases $x_{1}$ times and that of outer loop increases $x _{2}$ times
$\Rightarrow $ magnetic field at $P$
$B _{ P }=\left( x _{1} \frac{\mu_{0} i _{1}}{2 R }- x _{2} \frac{\mu_{0} i _{2}}{4 R }\right)$
For $B _{ P }=0, i _{2}=\left(\frac{ x _{1}}{ x _{2}}\right) \cdot\left(2 i _{1}\right)$
$\because B$ changes more rapidly as point $P$ come closer to circumference.
$\Rightarrow x _{1} > x _{2}$
Or $i _{2} >2 i _{1}$ (which is given condition)
So, there are points inside inner loop where magnetic field will be zero.

Q7. A Soft plastic bottle, filled with water of density $1\, gm / cc$, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of $5\, gm$, and it is made of a thick glass of density $2.5 \,gm / cc$. Initially the bottle is sealed at atmospheric pressure $p _{0}=10^{5} \,Pa$ so that the volume of the trapped air is $v _{0}=3.3\, cc$. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure $p _{0}+\Delta p$ without changing its orientation. At this pressure, the volume of the trapped air is $v _{0}-\Delta v$.
Let $\Delta v = X \,\,cc$ and $\Delta p = Y \times 10^{3} Pa$.
image
The value of $X$ is _______.

Answer: 0.30

Solution

For equilibrium of the test tube
$mg =\left( v _{\text {tube }}+ v _{\text {air }}\right) \rho_{ w } g$
So, $ 5=\left(\frac{5}{2.5}+v_{\text {air }}\right)$ (1)
So, $v_{\text {air }}=3\, cc$
So, $\Delta v =0.3\, cc$

Q8. A Soft plastic bottle, filled with water of density $1\, gm / cc$, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of $5\, gm$, and it is made of a thick glass of density $2.5 \,gm / cc$. Initially the bottle is sealed at atmospheric pressure $p _{0}=10^{5} \,Pa$ so that the volume of the trapped air is $v _{0}=3.3\, cc$. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure $p _{0}+\Delta p$ without changing its orientation. At this pressure, the volume of the trapped air is $v _{0}-\Delta v$.
Let $\Delta v = X \,\,cc$ and $\Delta p = Y \times 10^{3} Pa$.
image
The value of $Y$ is _______.

Answer: 10.00

Solution

For isothermal process
$\left(10^{5}\right)(3.3)=( P )(3)$
So, $P =1.1 \times 10^{5} Pa$
So, $\Delta P =(1.1-1) \times 10^{5}$
$=10 \times 10^{3} Pa$

Q9. A pendulum consists of a bob of mass $m =0.1\, kg$ and a massless inextensible string of length $L =1.0 \,m .$ It is suspended from a fixed point at height $H =0.9 \,m$ above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse $P =0.2\, kg - m / s$ is imparted to the bob at some instant. After the bob slides for some distance, the string becomes taut and the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is $J \,kg - m ^{2} / s$. The kinetic energy of the pendulum just after the lift-off is $K$ Joules.
The value of $J$ is ______.

Answer: 0.18

Solution

image
$J _{ i }= MV _{ i } H \sin 90^{\circ}$
$=0.2 \times 0.9=0.18 \,kg - m ^{2} / s$

Q10. A pendulum consists of a bob of mass $m =0.1\, kg$ and a massless inextensible string of length $L =1.0 \,m .$ It is suspended from a fixed point at height $H =0.9 \,m$ above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse $P =0.2\, kg - m / s$ is imparted to the bob at some instant. After the bob slides for some distance, the string becomes taut and the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is $J \,kg - m ^{2} / s$. The kinetic energy of the pendulum just after the lift-off is $K$ Joules.
The value of $K$ is ______.

Answer: 0.16

Solution

As bob lifts off due to impulse of string angular momentum will be conserved about suspension point
$\Rightarrow J _{ f }= J _{ i } $
$\Rightarrow Mv _{ f } \ell \sin 90^{\circ}=0.18 $
$\Rightarrow v _{ f }=1.8 \,m / s$
Kinetic energy after lifting off
$\Rightarrow K _{f}=\frac{1}{2} mv _{f}^{2}$
$=\frac{1}{2} \times 0.1 \times(1.8)^{2}=0.162\, J$

Q11. In the circuit, a metal filament lamp is connected in series with a capacitor of capacitance $C\, \mu F$ across a $200\, V , 50\, Hz$ supply. The power consumed by the lamp is $500\, W$ while the voltage drop across it is $100\, V$. Assume that there is no inductive load in the circuit. Take $r m s$ values of the voltages. The magnitude of the phase-angle (in degrees) between the current and supply voltage is $\phi .$ Assume, $\pi \sqrt{3} \approx 5$.
The value of $C$ is _____.

Answer: 100.00

Solution

image
$P _{\text {lamp }}=500 \,W$
$\Rightarrow V _{\text {lamp }} i _{\text {lamp }}=500$
$\Rightarrow (100) i _{\text {lamp }}=500$
$i _{\text {lamp }}=5 A$
Impedance of circuit $Z =\frac{ V _{\text {source }}}{ i _{\text {source }}}$
$=\frac{200}{5}=40\, \Omega$
Resistance of lamp $R =\frac{ V _{\text {lamp }}}{ i _{\text {source }}}$
$=20 \,\Omega$
Reactance of capacitance
$X _{ C }=\sqrt{ Z ^{2}- R ^{2}}=20 \sqrt{3} \Omega$
$\frac{1}{\omega C }=20 \sqrt{3}$
$C =\frac{1}{20 \sqrt{3} \times 2 \times \pi \times 50}$
$=100 \,\mu F$

Q12. In the circuit, a metal filament lamp is connected in series with a capacitor of capacitance $C\, \mu F$ across a $200\, V , 50\, Hz$ supply. The power consumed by the lamp is $500\, W$ while the voltage drop across it is $100\, V$. Assume that there is no inductive load in the circuit. Take $r m s$ values of the voltages. The magnitude of the phase-angle (in degrees) between the current and supply voltage is $\phi .$ Assume, $\pi \sqrt{3} \approx 5$.
The value of $\phi$ is _____.

Answer: 60.00

Solution

$\cos \phi=\frac{ R }{ Z }=\frac{20}{40}=\frac{1}{2}$
$\Rightarrow \phi=60^{\circ}$

Q13. A special metal S conducts electricity without any resistance. A closed wire loop, made of S, does not allow any change in flux through itself by inducing a suitable current to generate a compensating flux. The induced current in the loop cannot decay due to its zero resistance. This current gives rise to a magnetic moment which in turn repels the source of magnetic field or flux. Consider such a loop, of radius a, with its centre at the origin. A magnetic dipole of moment $m$ is brought along the axis of this loop from infinity to a point at distance $r(>>$ a) from the centre of the loop with its north pole always facing the loop, as shown in the figure below.
The magnitude of magnetic field of a dipole $m$, at a point on its axis at distance $r$, is $\frac{\mu_{0}}{2 \pi} \frac{ m }{ r ^{3}}$, where $\mu_{0}$ is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, $m _{1}$ and $m _{2}$, separated by a distance $r$ on the common axis, with their north poles facing each other, is $\frac{ km _{1} m _{2}}{ r ^{4}}$, where $k$ is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.
image
When the dipole $m$ is placed at a distance $r$ from the center of the loop (as shown in the figure), the current induced in the loop will be proportional to

A

$m / r ^{3}$

B

$m ^{2} / r ^{2}$

C

$m / r ^{2}$

D

$m ^{2} / r$

Solution

$\frac{\mu_{0}}{2 \pi} \frac{m}{r^{3}}=\frac{\mu_{0} i_{1}}{2 a}$
$\Rightarrow i_{1} \propto \frac{m}{r^{3}}$

Q14. A special metal S conducts electricity without any resistance. A closed wire loop, made of S, does not allow any change in flux through itself by inducing a suitable current to generate a compensating flux. The induced current in the loop cannot decay due to its zero resistance. This current gives rise to a magnetic moment which in turn repels the source of magnetic field or flux. Consider such a loop, of radius a, with its centre at the origin. A magnetic dipole of moment $m$ is brought along the axis of this loop from infinity to a point at distance $r(>>$ a) from the centre of the loop with its north pole always facing the loop, as shown in the figure below.
The magnitude of magnetic field of a dipole $m$, at a point on its axis at distance $r$, is $\frac{\mu_{0}}{2 \pi} \frac{ m }{ r ^{3}}$, where $\mu_{0}$ is the permeability of free space. The magnitude of the force between two magnetic dipoles with moments, $m _{1}$ and $m _{2}$, separated by a distance $r$ on the common axis, with their north poles facing each other, is $\frac{ km _{1} m _{2}}{ r ^{4}}$, where $k$ is a constant of appropriate dimensions. The direction of this force is along the line joining the two dipoles.
image
The work done in bringing the dipole from infinity to a distance $r$ from the center of the loop by the given process is proportional to

A

$m / r ^{5}$

B

$m ^{2} / r ^{5}$

C

$m ^{2} / r ^{6}$

D

$m ^{2} / r ^{7}$

Solution

$dW = F . d x =\frac{- Km \left( i _{1} \pi a ^{2}\right)}{ r ^{4}}( dr )$
$i _{1}=\frac{ ma }{\pi r ^{3}}$
$W =\int\limits_{\infty}^{r} \frac{ km \left(\frac{ ma }{\pi r ^{3}} \times \pi a ^{2}\right) dr }{ r ^{3}}= km ^{2} a ^{3} \int \frac{ dr }{ r ^{7}}$
$W \alpha \frac{ m ^{2}}{ r ^{6}}$

Q15. A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, $C _{ V }=2 R$. Here, $R$ is the gas constant. Initially, each side has a volume $V _{0}$ and temperature $T_{0}$. The left side has an electric heater, which is turned on at very low power to transfer heat $Q$ to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to $V _{0} / 2$. Consequently, the gas temperatures on the left and the right sides become $T _{ L }$ and $T _{ R }$, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.
image
The value of $\frac{ T _{ R }}{ T _{0}}$ is

A

$\sqrt{2}$

B

$\sqrt{3}$

C

$2$

D

$3$

Solution

image
Pressure on either side is equal
$C _{ V }=2 R ; C _{ P }=3 R \Rightarrow \gamma=3 / 2$
image
Left chamber
$Q =\Delta U _{1}+\Delta W _{1}$
Right chamber
$0=\Delta U _{2}+\Delta W _{2}$
$\Delta W _{1}+\Delta W _{2}=0$
$\Rightarrow Q =\Delta U _{1}+\Delta U _{2}$
$=2 R \left( T _{ L }- T _{0}\right)+2 R \left( T _{ R }- T _{0}\right)$ ... (i)
Also pressure each side of piston is equal
$\Rightarrow \frac{ RT _{ L }}{3 V _{0} / 2}=\frac{ RT _{ R }}{ V _{0} / 2}$ ...(ii)
$\Rightarrow \left( T _{ L } / 3\right)= T _{ R }$
For right chamber $\Rightarrow $ adiabatic compression
$\Rightarrow TV ^{\gamma-1}=$ constant
$T _{0} V _{0}^{0.5}= T _{ R }\left(\frac{ V _{0}}{2}\right)^{0.5}$
$ \Rightarrow T _{ R }=\sqrt{2} T _{0}$
$\Rightarrow T _{ L }=3 \sqrt{2} T _{0}$
$\frac{ T _{ R }}{ T _{0}}=\sqrt{2}$

Q16. A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, $C _{ V }=2 R$. Here, $R$ is the gas constant. Initially, each side has a volume $V _{0}$ and temperature $T_{0}$. The left side has an electric heater, which is turned on at very low power to transfer heat $Q$ to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to $V _{0} / 2$. Consequently, the gas temperatures on the left and the right sides become $T _{ L }$ and $T _{ R }$, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.
image
The value of $\frac{ Q }{ RT _{0}}$ is

A

$4(2 \sqrt{2}+1)$

B

$4(2 \sqrt{2}-1)$

C

$(5 \sqrt{2}+1)$

D

$(5 \sqrt{2}-1)$

Solution

image
Pressure on either side is equal
$C _{ V }=2 R ; C _{ P }=3 R \Rightarrow \gamma=3 / 2$
image
Left chamber
$Q =\Delta U _{1}+\Delta W _{1}$
Right chamber
$0=\Delta U _{2}+\Delta W _{2}$
$\Delta W _{1}+\Delta W _{2}=0$
$\Rightarrow Q =\Delta U _{1}+\Delta U _{2}$
$=2 R \left( T _{ L }- T _{0}\right)+2 R \left( T _{ R }- T _{0}\right)$ ... (i)
Also pressure each side of piston is equal
$\Rightarrow \frac{ RT _{ L }}{3 V _{0} / 2}=\frac{ RT _{ R }}{ V _{0} / 2}$ ...(ii)
$\Rightarrow \left( T _{ L } / 3\right)= T _{ R }$
$Q =2 R \left(3 \sqrt{2} T _{0}- T _{0}\right)=2 R \left(\sqrt{2} T _{0}- T _{0}\right)$
$=8 \sqrt{2} RT _{0}-4 RT _{0}$
$\Rightarrow \frac{ Q }{ RT _{0}}=8 \sqrt{2}-4$

Q17. In order to measure the internal resistance $r_{1}$ of a cell of emf $E$, a meter bridge of wire resistance $R_{0}=50\, \Omega$, a resistance $R _{0} / 2$, another cell of emf $E / 2$ (internal resistance $r$ ) and a galvanometer $G$ are used in a circuit, as shown in the figure. If the null point is found at $\ell=72\, cm$, then the value of $r _{1}=$ _____ $\Omega$

Answer: 3

Solution

image
$R _{ AB }=50\, \Omega$
So, $R _{\Lambda P }=\frac{50}{100} \times 72=36 \,\Omega$
$I =\frac{\varepsilon}{ r _{1}+50+25}$ ...(i)
$-36 I -\frac{\varepsilon}{2}- Ir _{1}+\varepsilon=0$
Solving equation (i) and (ii)
$r _{1}=3 \,\Omega$

Q18. The distance between two stars of masses $3 M _{ S }$ and $6 M _{ s }$ is $9 R$. Here $R$ is the mean distance between the centers of the Earth and the Sun, and $M _{ S }$ is the mass of the Sun. The two stars orbit around their common centre of mass in circular orbits with period $nT$, where $T$ is the period of Earth's revolution around the Sun. The value of $n$ is ______.

Answer: 9

Solution

image
Both will revolve about common center of mass
$x=\frac{3 M_{s}}{6 M_{s}+3 M_{s}} \times 9 R=3 R $ ... (i)
$\frac{G 6 M_{s} \times 3 M_{s}}{(9 R)^{2}}=6 M_{s}\left(\omega^{2} x\right)$ .... (ii)
Solving equation (i) and (ii) we get
$\omega^{2} =\frac{ GM _{ S }}{81 R ^{3}} $
$T ^{\prime 2} =\frac{4 \pi^{2} R ^{3}}{ GM _{ S }} \times 81$ ... (iii)
For the motion of earth around Sun
$T ^{2}=\frac{4 \pi^{2} R ^{3}}{ GM _{ s }}$ .... (iv)
From (iii) and (iv)
$ T ^{\prime 2}=81 T ^{2} $
$ T ^{\prime}=9 T$

Q19. In a photoemission experiment, the maximum kinetic energies of photoelectrons from metals $P , Q$ and $R$ are $E_{P}, E_{Q}$ and $E_{R}$, respectively, and they are related by $E_{P}=2 E_{Q}=2 E_{R}$. In this experiment, the same source of monochromatic light is used for metal $P$ and $Q$ while a different source of monochromatic light is used for the metal $R$. The work functions for metals $P, Q$ and $R$ are $4.0\, eV , 4.5\, eV$ and $5.5 \,eV$, respectively. The energy of the incident photon used for metal $R$, in $e V$, is ______.

Answer: 6

Solution

Let $E _{ R }= E$
Then $E _{ Q }= E$
$E _{ P }=2 E$
From Einstein's equation for $P , Q$ and $R$
$2 E = hv -4.0 \ldots$ (i)
$E = hv -4.5 \ldots$ (ii)
$E = hv ^{\prime}-5.5 $...(iii)
Solving equation (i) and (ii) we get
$E =0.5$
So, $hv ^{\prime}=6.0 \,eV$

JEE Advanced Chemistry Question Paper with Solution JEE Advanced 2021 Paper 2

Q1. The reaction sequence (s) that would lead to $o$-xylene as the major product is (are)

A

B

C

D

Solution

image
image
image
image

Q2. Correct options for the following sequence of reactions is (are)

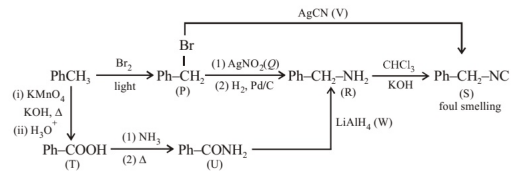
A

$Q=K N O_{2}, W=L i A 1 H_{4}$

B

$R=$ benzenamine, $V=K C N$

C

$Q= AgNO _{2}, R=$ phenylmethanamine

D

$W=L i A l H_{4}, V=A g C N$

Q3. For the following reaction $2 X+Y \xrightarrow{k} P$ the rate of reaction is $\frac{d[P]}{d t}=k[X]$. Two moles of $X$ are mixed with one mole of $Y$ to make $1.0\, L$ of solution. At $50 \,s$, $0.5$ mole of $Y$ is left in the reaction mixture. The correct statement(s) about the reaction is(are)
(Use : $\ln\,2 = 0.693)$

A

The rate constant, $k$, of the reaction is $13.86 \times 10^{-4} s ^{-1}$.

B

Half-life of $X$ is $50\, s$.

C

At $50\, s,-\frac{d[X]}{d t}=13.86 \times 10^{-3} mol\, L^{-1} s^{-1}$.

D

At $100 \,s,-\frac{d[Y]}{d t}=3.46 \times 10^{-3} mol\, L^{-1} s^{-1}$.

Solution

image
rate $=-\frac{1}{2} \frac{ d x }{ dt }=-\frac{ dy }{ dt }=\frac{ dP }{ dt }= K [ X ]$
$-\frac{1}{2} \frac{ d x }{ dt }= K [ X ]$
$-\frac{ dx }{ dt }=2 K [ X ]= K ^{1}[ X ]$
Half life is $t =50 \,sec$
$2 K =\frac{0.653 L }{50}$
$K =\frac{0.6932}{100}=6.332 \times 10^{-3}$
$t = 5 0 \,sec$
$-\frac{ dx }{ dt }=2 K [ X ]$
$-\frac{ dx }{ dt }=2 \times 6.332 \times 10^{-3} \times 1$
$=13.864 \times 10^{-3} mole / L / Sec$
$-\frac{ dy }{ dt }= K [ X ]=6.332 \times 10^{-3}\left(\frac{1}{2}\right)$
$=3.46 \times 10^{-3} mole / L / Sec ^{-1}$

Q4. Some standard electrode potentials at $298\, K$ are given below:
$Pb ^{2+} / Pb -0.13 \,V $
$ Ni ^{2+} Ni -0.24 \,V $
$ Cd ^{2+} / Cd -0.40 \,V $
$ Fe ^{2+} / Fe -0.44\, V$
To a solution containing $0.001 \,M$ of $X ^{2+}$ and $0.1 \,M$ of $Y ^{2+}$, the metal rods $X$ and $Y$ are inserted (at $298\, K$ ) and connected by a conducting wire. This resulted in dissolution of $X$. The correct combination(s) of $X$ and $Y$, respectively, is(are)
(Given: Gas constant, $R =8.314 \,J \,K ^{-1}\, mol ^{-1}$,
Faraday constant, $F =96500\, C \,mol ^{-1}$ )

A

$Cd$ and $Ni$

B

$Cd$ and $Fe$

C

$Ni$ and $Pb$

D

$Ni$ and $Fe$

Solution

(A) $ Cd + Ni ^{+2} \longrightarrow Cd ^{+2}+ Ni$
$ E _{ cell }=0.40+(-24)-\frac{0.0591}{2} \log \frac{0.001}{0.1}$
$=0.16+\frac{0.0591}{2} \times 2$
$=6.64+0.551=0.71(+ ve )$
(B) $ E _{\text {cell }}=0.40+(-0.44)-\frac{0.591}{2} \log \frac{0.01}{0.1}$
$=-0.04+\frac{0.591}{2} \times 2$
$=-0.04+0.06=0.02(+ ve )$
(C) $ E _{\text {cell }}=0.24+(-0.13)+\frac{.0591}{2} \times 2 $
$=0.11+0.06=0.33(+ ve )$
(D) $E _{\text {cell }}=0.24+(-0.44)+\frac{0.0591}{2} \times 2$
$=-0.20+0.06=-0.14(- ve )$

Q5. The pair(s) of complexes wherein both exhibit tetrahedral geometry is(are)
(Note: $py =$ pyridine
Given: Atomic numbers of $Fe , Co , Ni$ and $Cu$ are $26,27,28$ and $29$ , respectively)

A

$\left[ FeCl _{4}\right]^{-}$and $\left[ Fe ( CO )_{4}\right]^{2-}$

B

$\left[ Co ( CO )_{4}\right]^{-}$and $\left[ CoCl _{4}\right]^{2-}$

C

$\left[ Ni ( CO )_{4}\right]$ and $\left[ Ni ( CN )_{4}\right]^{2-}$

D

$\left[ Cu ( py )_{4}\right]^{+}$and $\left[ Cu ( CN )_{4}\right]^{3-}$

Solution

(A) $\left[ FeCl _{4}\right]^{-}$
$Fe ^{+3}=3 d ^{5}, Cl ^{-}$ weak field liganol $sp ^{3}$
$\left[ Fe ( CO )_{4}\right]^{-2}$
$Fe ^{-2} =3 d ^{8} 4 s ^{2}$
$CO$ strong field liganol pairing occurs
$Fe ^{-2}=3 d ^{10}$
hence $sp ^{3}$
(B) $\left[ Co ( CO )_{4}\right]^{-}$
$Co =3 d ^{8} 4 s ^{2} $
due to $CO$ pairing occurs
Hence $=3 d ^{10}$
$\left[ CoCl _{4}\right]^{-2}$
$Co ^{+2}=3 d ^{7}$,
$Cl ^{-}$ weak field liganol $sp ^{3}$
(D) $\left[ Cu ( Py )_{4}\right]^{+1}$
$Cu ^{+1}=3 d ^{10}, sp ^{3}$
$\left[ Cu ( CN )_{4}\right]^{-3}$
$Cu ^{+1}=3 d ^{10}, sp ^{3}$

Q6. The correct statement(s) related to oxoacids of phosphorous is(are)

A

Upon heating, $H _{3} PO _{3}$ undergoes disproportionation reaction to produce $H _{3} PO _{4}$ and $PH _{3}$.

B

While $H _{3} PO _{3}$ can act as reducing agent, $H _{3} PO _{4}$ cannot.

C

$H _{3} PO _{3}$ is a monobasic acid.

D

The $H$ atom of $P - H$ bond in $H _{3} PO _{3}$ is not ionizable in water.

Solution

$H_3PO_3 \xrightarrow{\Delta} H_3PO_4 + PH_3$
image
$P - H$ bond is responsible for it is reducing character, $H _{3} PO _{4}$ doesnot have.
$H _{3} PO _{3}$ is a dibasic acid in oxyacids of phosphors $O - H$ bond is ionisable where as $P - H$ bond is non ionizable.

Q7. At $298\, K$, the limiting molar conductivity of a weak monobasic acid is $4 \times 10^{2} S\, cm ^{2} mol ^{-1} .$ At $298 \,K$, for an aqueous solution of the acid the degree of dissociation is $\alpha$ and the molar conductivity is $y \times 10^{2} \,S \,cm ^{2} mol ^{-1}$. At $298\, K$, upon $20$ times dilution with water, the molar conductivity of the solution becomes $3 y \times 10^{2} S \,cm ^{2} mol ^{-1}$
The value of $\alpha$ is _______.

Answer: 0.22

Solution

$\alpha_{1}=\frac{\Lambda_{ m }^{ c }}{\Lambda_{ m }^{0}}=\frac{ y \times 10^{2}}{4 \times 10^{2}}=\frac{ y }{4}=\alpha$
On dilution conductivity increases three times
$\alpha_{2}=\frac{3 y \times 10^{2}}{4 \times 10^{2}}=3 \alpha_{1}=3 \alpha$
image
$K _{ a }=\frac{ C \alpha^{2}}{1-\alpha}$
Since temperature is constant $K _{ a }$ will be constant
$\frac{C_{1} \alpha_{1}^{2}}{1-\alpha_{1}}=\frac{C_{2} \alpha_{2}^{2}}{1-\alpha_{2}} $
$\frac{C \times \alpha^{2}}{1-\alpha}=\frac{\left(\frac{C}{20}\right)(3 \alpha)^{2}}{1-3 \alpha} $
$\frac{1}{1-\alpha}=\frac{9}{20}-\frac{1}{(1-3 \alpha)} $
$20-60 \alpha=9-9 \alpha ; $
$\alpha=\frac{11}{51}=0.2156 $
$\alpha=0.22$

Q8. At $298\, K$, the limiting molar conductivity of a weak monobasic acid is $4 \times 10^{2} S\, cm ^{2} mol ^{-1} .$ At $298 \,K$, for an aqueous solution of the acid the degree of dissociation is $\alpha$ and the molar conductivity is $y \times 10^{2} \,S \,cm ^{2} mol ^{-1}$. At $298\, K$, upon $20$ times dilution with water, the molar conductivity of the solution becomes $3 y \times 10^{2} S \,cm ^{2} mol ^{-1}$
The value of $y$ is _______.

Answer: 0.88

Solution

On dilution conductivity increases three times
Since temperature is constant $K _{ a }$ will be constant
$
\frac{C_{1} a_{1}^{2}}{1-a_{1}}=\frac{C_{2} a_{2}^{2}}{1-a_{2}}
$
$
\begin{array}{l}
\Rightarrow \frac{C \times a^{2}}{1-a}=\frac{\left(\frac{C}{20}(3 a)^{2}\right)}{(1-3 a)} \\
\Rightarrow \frac{1}{1-a}=\frac{9}{20(1-3 a)} \\
\Rightarrow 20-60 a=9-9 a \\
\Rightarrow a=\frac{11}{51}=0.2156 \\
\Rightarrow a=0.22
\end{array}
$
$
a=\frac{y}{4} ; y=4 a=4 \times 0.22=0.88
$
From above question we found the value of $a$.

Q9. Reaction of $x \,g$ of $S n$ with $H C l$ quantitatively produced a salt. Entire amount of the salt reacted with $y \,g$ of nitrobenzene in the presence of required amount of $HCl$ to produce $1.29\, g$ of an organic salt (quantitatively).
(Use Molar masses (in $g \,mol ^{-1}$ ) of $H , C , N , O , Cl$ and $Sn$ as $1,12,14,16,35$ and $119$ , respectively).
The value of $x$ is _______.

Answer: 3.57

Solution

$Sn + 2HCl \rightarrow SnCl_2 + H_2$
image
Moles of $Sn =\frac{ x }{119}$
Moles of nitrobenzene $=\frac{ x }{119} \times \frac{1}{3}$
Moles of anilium chloride $=\frac{x}{119} \times \frac{1}{3}$
Moles of nitrobenzene $=\frac{x}{357}$
$\frac{ y }{123}=\frac{ x }{357}$ ... (1)
Moles of anilium chloride $=\frac{x}{357}$ ... (2)
$\frac{1.29}{129}=\frac{x}{357}$
$x=3.57$

Q10. Reaction of $x \,g$ of $S n$ with $H C l$ quantitatively produced a salt. Entire amount of the salt reacted with $y \,g$ of nitrobenzene in the presence of required amount of $HCl$ to produce $1.29\, g$ of an organic salt (quantitatively).
(Use Molar masses (in $g \,mol ^{-1}$ ) of $H , C , N , O , Cl$ and $Sn$ as $1,12,14,16,35$ and $119$ , respectively).
The value of $y$ is _______.

Answer: 1.23

Solution

$Sn + 2HCl \rightarrow SnCl_2 + H_2$
image
Moles of $Sn =\frac{ x }{119}$
Moles of nitrobenzene $=\frac{ x }{119} \times \frac{1}{3}$
Moles of anilium chloride $=\frac{x}{119} \times \frac{1}{3}$
Moles of nitrobenzene $=\frac{x}{357}$
$\frac{ y }{123}=\frac{ x }{357}$ ... (1)
Moles of anilium chloride $=\frac{x}{357}$ ... (2)
$y =1.225 \cong 1.23$

Q11. A sample $(5.6 \,g )$ containing iron is completely dissolved in cold dilute $HCl$ to prepare a $250\, mL$ of solution. Titration of $25.0 \,mL$ of this solution requires $12.5\, mL$ of $0.03 \,M \,KMnO _{4}$ solution to reach the end point. Number of moles of $Fe ^{2+}$ present in $250\, mL$ solution is $x \times 10^{-2}$ (consider complete dissolution of $FeCl _{2}$ ). The amount of iron present in the sample is $y \%$ by weight.
(Assume: $KMnO _{4}$ reacts only with $Fe ^{2+}$ in the solution
Use: Molar mass of iron as $56 \,g \,mol ^{-1}$ )
The value of $x$ is _______.

Answer: 1.875

Solution

meq of $Fe ^{+2}=$ meq of $KMnO _{4}$
$x \times 10^{-2} \times 1000 \times 1=12.5 \times 0.03 \times 5 \times 10$
$x =1.875 \,mole$

Q12. A sample $(5.6 \,g )$ containing iron is completely dissolved in cold dilute $HCl$ to prepare a $250\, mL$ of solution. Titration of $25.0 \,mL$ of this solution requires $12.5\, mL$ of $0.03 \,M \,KMnO _{4}$ solution to reach the end point. Number of moles of $Fe ^{2+}$ present in $250\, mL$ solution is $x \times 10^{-2}$ (consider complete dissolution of $FeCl _{2}$ ). The amount of iron present in the sample is $y \%$ by weight.
(Assume: $KMnO _{4}$ reacts only with $Fe ^{2+}$ in the solution
Use: Molar mass of iron as $56 \,g \,mol ^{-1}$ )
The value of $y$ is _______.

Answer: 18.75

Solution

Moles of $Fe ^{+2}= x \times 10^{-2}=1.875 \times 10^{-2}$
wt. of $Fe ^{+2}=1.875 \times 10^{-2} \times 56$
Hence percentage of $Fe ^{+2}$
$=\frac{1.875 \times 10^{-2} \times 56}{5.6} \times 100 \%$
$=18.75 \%$

Q13. The amount of energy required to break a bond is same as the amount of energy released when the same bond is formed. In gaseous state, the energy required for homolytic cleavage of a bond is called Bond Dissociation Energy (BDE) or Bond Strength. BDE is affected by $s$-character of the bond and the stability of the radicals formed. Shorter bonds are typically stronger bonds. BDEs for some bonds are given below:
image
Correct match of the $C-H$ bonds (shown in bold) in Column $J$ with their BDE in Column $K$ is
Column $J$ Molecule Column II $K$ BDE($kal \, mol^{-1})$
P $H - CH(CH_3)_2$ i 132
Q $H - CH_2Ph$ ii 110
R $H - CH = CH_2$ iii 95
S $H - C \equiv CH$ iv 88

A

$P - iii, Q - iv, R - ii, S - i$

B

$P - i, Q - ii, R - iii, S - iv$

C

$P - iii, Q - ii, R -i, S - iv$

D

$P - ii, Q - i, R - iv, S - iii$

Solution

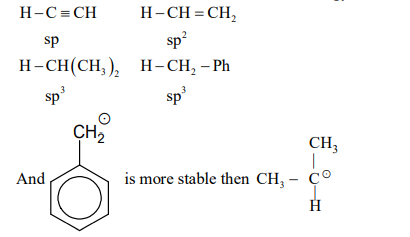
As $S$ character increases bond dissociation energy increases
image

Q14. The amount of energy required to break a bond is same as the amount of energy released when the same bond is formed. In gaseous state, the energy required for homolytic cleavage of a bond is called Bond Dissociation Energy (BDE) or Bond Strength. BDE is affected by $s$-character of the bond and the stability of the radicals formed. Shorter bonds are typically stronger bonds. BDEs for some bonds are given below:
image
For the following reaction
$CH_4(g) + Cl_2(g) \xrightarrow{\text{light}}CH_3Cl(g) + HCl(g)$
The correct statement is

A

Initiation step is exothermic with $\Delta H ^{\circ}=-58 \,kcal \,mol ^{-1}$.

B

Propagation step involving ${ }^{\circ} CH _{3}$ formation is exothermic with $\Delta H ^{\circ}=-2\, kcal\, mol ^{-1}$.

C

Propagation step involving $CH _{3} Cl$ formation is endothermic with $\Delta H ^{\circ}=+27\, kcal\, mol ^{-1}$.

D

The reaction is exothermic with $\Delta H ^{\circ}=-25\, kcal\, mol ^{-1}$.

Solution

$CH _{4}+ Cl _{2} \xrightarrow{\text { light }} CH _{3} Cl + HCl$ this reaction is obtained from given reaction.
$CH _{3}- H \longrightarrow CH _{3}^{\odot}+ H ^{\circ} \ldots(1)$
$Cl - Cl \longrightarrow Cl ^{\circ}+ Cl ^{\circ} $...(2)
$CH _{3}- Cl \longrightarrow CH _{3}{ }^{\circ}+ Cl ^{\circ}$ ...(3)
$H - Cl \longrightarrow H ^{\circ}+ Cl ^{\circ}$ ...(4)
$(1)+(2)-(3)-(4)$
Hence $\Delta H =105+58-85-103=-25 \,KCal / mole$

Q15. The reaction of $K _{3}\left[ Fe ( CN )_{6}\right]$ with freshly prepared $FeSO _{4}$ solution produces a dark blue precipitate called Turnbull's blue. Reaction of $K _{4}\left[ Fe ( CN )_{6}\right]$ with the $FeSO _{4}$ solution in complete absence of air produces a white precipitate $X$, which turns blue in air. Mixing the $FeSO _{4}$ solution with $NaNO _{3}$, followed by a slow addition of concentrated $H _{2} SO _{4}$ through the side of the test tube produces a brown ring.
Precipitate $X$ is

A

$Fe _{4}\left[ Fe ( CN )_{6}\right]_{3}$

B

$Fe \left[ Fe ( CN )_{6}\right]$

C

$K _{2} Fe \left[ Fe ( CN )_{6}\right]$

D

$KFe \left[ Fe ( CN )_{6}\right]$

Solution

$FeSO_4 + K_4[Fe(CN)_6] \rightarrow \underset{\text{White ppt.}}{K_2[Fe(CN)_6]}$

Q16. The reaction of $K _{3}\left[ Fe ( CN )_{6}\right]$ with freshly prepared $FeSO _{4}$ solution produces a dark blue precipitate called Turnbull's blue. Reaction of $K _{4}\left[ Fe ( CN )_{6}\right]$ with the $FeSO _{4}$ solution in complete absence of air produces a white precipitate $X$, which turns blue in air. Mixing the $FeSO _{4}$ solution with $NaNO _{3}$, followed by a slow addition of concentrated $H _{2} SO _{4}$ through the side of the test tube produces a brown ring.
Among the following, the brown ring is due to the formation of

A

$\left[ Fe ( NO )_{2}\left( SO _{4}\right)_{2}\right]^{2-}$

B

$\left[ Fe ( NO )_{2}\left( H _{2} O \right)_{4}\right]^{3+}$

C

$\left[ Fe ( NO )_{4}\left( SO _{4}\right)_{2}\right]$

D

$\left[ Fe ( NO )\left( H _{2} O \right)_{5}\right]^{2+}$

Solution

$FeSO _{4}+ NaNO _{3}+ H _{2} SO _{4} \longrightarrow \left[ Fe \left( H _{2} O \right)_{5} NO \right]^{+2}+ SO _{4}^{-2}$

Q17. One mole of an ideal gas at $900\, K$, undergoes two reversible processes, $I$ followed by $II$, as shown below. If the work done by the gas in the two process are same, the value of $\ln \frac{ V _{3}}{ V _{2}}$ ____
image
( $U$ : internal energy, $S$ : entropy, $p$ : pressure, $V:$ volume, $R$ : gas constant)
(Given: molar heat capacity at constant volume, $C_{v, m}$ of the gas is $\frac{5}{2} R$ )

Answer: 10

Solution

$1^{\text {st }}$ process is adiabatic since entropy is constant.
$W _{1}=\Delta U$
$\Delta U =450\, R -2250 \, R =-1800\, R $
$ W _{1}=-1800 \, R$ .... (1)
In $2^{\text {nd }}$ process internal energy is constant it means it is a isothermal process.
$W _{2} =-2.303 \, n RT \log \frac{ V _{3}}{ V _{2}} $ ... (2)
$=- nRT \ln \frac{ V _{3}}{ V _{2}}$ ... (3)
Given, $n =1$ mole, here temperature is unknown
$U = nC _{ V } T $ for process $II$
$450 \,R =1 \times \frac{5}{2} RT$
$ T =\frac{450 \times 2}{5}=180\, K$
Equation (1) = equation (2)
$W _{1}= W _{2}$
$-1800 \,R =-1 \times R \times 180 \ln \frac{ V _{3}}{ V _{2}}$
$\ln \frac{ V _{3}}{ V _{2}}=\frac{1800}{180}=10$

Q18. Consider a helium $(He)$ atom that absorbs a photon of wavelength $330\, nm$. The change in the velocity (in $cm \,s ^{-1}$ ) of $He$ atom after the photon absorption is
(Assume: Momentum is conserved when photon is absorbed.
Use: Planck constant $=6.6 \times 10^{-34} J s$, Avogadro number $=6 \times 10^{23} mol ^{-1}$,
Molar mass of $He =4\, g\, mol ^{-1}$ )

Answer: 30

Solution

$\lambda=\frac{ h }{ m (\Delta V )}$
$330 \times 10^{-9}=\frac{6.6 \times 10^{-34}}{\left(\frac{4 \times 10^{-3}}{6 \times 10^{23}}\right) \times \Delta V }$
$\Delta V =\frac{6.6 \times 6 \times 10^{23} \times 10^{-34}}{4 \times 10^{-3} \times 330 \times 10^{-9}}$
$=0.30 \,m / s$
$=0.30 \times 100\, cm / s$
$=30 \,cm / s$

Q19. Ozonolysis of $ClO _{2}$ produces an oxide of chlorine. The average oxidation state of chlorine in this oxide is _____ .

Answer: 6

Solution

$2 ClO _{2}+2 O _{3} \longrightarrow Cl _{2} O _{6}+2 O _{2}$
Average oxidization state of $Cl$ atom is $+6$

JEE Advanced Mathematics Question Paper with Solution JEE Advanced 2021 Paper 2

Q1. Let $S_{1}=\{( i , j , k ): i , j , k \in\{1,2, \ldots ., 10\}\},$
$ S_{2}=\{( i , j ): 1 \leq i < j +2 \leq 10, i , j \in\{1,2, \ldots . .10\}\},$
$ S_{3}=\{( i , j , k , l ): 1 \leq i < j < k < l , i , j , k , l \in\{1,2, \ldots ., 10\}\}$ and
$ S_{4}=\{( i , j , k , l ): i , j , k $ and $ l$ are distinct elements in $\{1,2, \ldots ., 10\}\}$
If the total number of elements in the set $S_{ r }$ is $n_{ r }, r =1,2,3,4$, then which of the following statements is(are) TRUE?

A

$n_{1}=1000$

B

$n_{2}=44$

C

$n_{3}=220$

D

$\frac{ n _{4}}{12}=420$

Solution

$n _{1}=10 \times 10 \times 10=10^{3}$
$n _{2}={ }^{8} C _{2}+2{ }^{8} C _{1}=44$
$n _{3}={ }^{10} C _{4}=210$
$n _{4}={ }^{10} P _{4}=5040$

Q2. Consider a triangle $P Q R$ having sides of lengths $p, q$ and $r$ opposite to the angles $P, Q$ and $R$, respectively. Then which of the following statements is(are) TRUE?

A

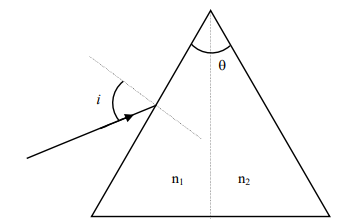
$\cos P \geq 1-\frac{ p ^{2}}{2 qr }$

B

$\cos R \geq\left(\frac{q-r}{p+q}\right) \cos P+\left(\frac{p-r}{p+q}\right) \cos Q$

C

$\frac{q+r}{p} < 2 \frac{\sqrt{\sin Q \sin R}}{\sin P}$

D

If $p < q$ and $p < r$, then $\cos Q >\frac{ p }{ r }$ and $\cos R >\frac{ p }{ q }$

Solution

(A) $\cos P =\frac{ q ^{2}+ r ^{2}- p ^{2}}{2 qr }, q ^{2}+ r ^{2} \geq 2 qr$,
by A.M. $\geq$ G.M
$\Rightarrow \cos P \geq 1-\frac{ p ^{2}}{2 qr }$
(B) By triangle inequality $q+p>r$
by projection formula
$r \cos P+p \cos R+q \cos R+r \cos Q>p \cos Q+q \cos P $
$\Rightarrow \cos R>\frac{(q-r)}{(p+q)} \cos P+\frac{(p-r)}{(p+q)} \cos Q$
So inequality is true (equality does not hold)
(C) By AM. $\geq$ GM.
$q+r \geq 2 \sqrt{q r} $
$\frac{q+r}{p} \geq \frac{2 \sqrt{q r}}{p}$
$\frac{\sin P}{p}=\frac{\sin Q}{q}=\frac{\sin R}{r} $ by sine rule
$\frac{q+r}{p} \geq \frac{2 \sqrt{\sin Q \sin R}}{\sin P}$
(D) If $\cos Q > \frac{p}{r} \Rightarrow r \cos Q>p$ ... (i)
$\cos R>\frac{p}{q} \Rightarrow q \cos R>p \ldots$ (ii)
Add (i) and (ii)
$r \cos Q+q \cos R>2 P \Rightarrow p>2 p$
$\Rightarrow p <0$, false

Q3. Let $f:\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \rightarrow R$ be a continuous function such that $f(0)=1$ and $\int\limits_{0}^{\frac{\pi}{3}} f(t) d t=0$. Then which of the following statements is(are) TRUE?

A

The equation $f ( x )-3 \cos 3 x =0$ has at least one solution in $\left(0, \frac{\pi}{3}\right)$

B

The equation $f ( x )-3 \sin 3 x =-\frac{6}{\pi}$ has at least one solution in $\left(0, \frac{\pi}{3}\right)$

C

$\displaystyle\lim _{x \rightarrow 0} \frac{x \int\limits_{0}^{x} f(t) d t}{1-e^{x^{2}}}=-1$

D

$\displaystyle\lim _{x \rightarrow 0} \frac{\sin x \int\limits_{0}^{x} f(t) d t}{x^{2}}=-1$

Solution

(A) Let $g(x) = f(x) - 3\cos\,3x$
$\int\limits_{0}^{\pi / 3} g(x) d x=\int\limits_{0}^{\pi / 3}(f(x)-3 \cos\, 3 x) d x$
$=\int\limits_{0}^{\pi / 3} f(x) d x-\int\limits_{0}^{\pi / 3} 3 \cos \,3 x \,d x=0 $
$\Rightarrow g(x)=0 $ has at least one solution in $[0, \pi / 3]$
(B) Let $h ( x )= f ( x )-3 \sin\, 3 x +6 / \pi$
$\int\limits_{0}^{\pi / 3} h(x)=\int\limits_{0}^{\pi / 3}\left(f(x)-3 \sin \,3 x+\frac{6}{\pi}\right) d x=0$
$\Rightarrow h(x)=0$ has at least one solution in $[0, \pi / 3]$
(C) $\displaystyle\lim _{x \rightarrow 0} \frac{\int\limits_{0}^{x} f(t) d t}{x}=\displaystyle\lim _{x \rightarrow 0} \frac{f(x)}{1}=f(0)=1$
$\Rightarrow \displaystyle\lim _{x \rightarrow 0} \frac{x \int\limits_{0}^{x} f(t) d t}{x^{2}\left(\frac{1-e^{x^{2}}}{x^{2}}\right)}=\displaystyle\lim _{x \rightarrow 0} \frac{-\int\limits_{0}^{x} f(t)}{x} \cdot \frac{x^{2}}{\left(e^{x^{2}}-1\right)}=-1$
(D) $\displaystyle\lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \frac{\int\limits_{0}^{x} f(t)}{x}=1$

Q4. For any real numbers $\alpha$ and $\beta$, let $y _{\alpha, \beta}( x ), x \in R$, be the solution of the differential equation $\frac{d y}{d x}+\alpha y=x e^{\beta x}, y(1)=1$.
Let $S=\left\{y_{\alpha, \beta}(x): \alpha, \beta \in R\right\}$. Then which of the following functions belong(s) the set $S$ ?

A

$f(x)=\frac{x^{2}}{2} e^{-x}+\left(e-\frac{1}{2}\right) e^{-x}$

B

$f(x)=-\frac{x^{2}}{2} e^{-x}+\left(e+\frac{1}{2}\right) e^{-x}$

C

$f(x)=\frac{e^{x}}{2}\left(x-\frac{1}{2}\right)+\left(e-\frac{e^{2}}{4}\right) e^{-x}$

D

$f(x)=\frac{e^{x}}{2}\left(\frac{1}{2}-x\right)+\left(e+\frac{e^{2}}{4}\right) e^{-x}$

Solution

$\frac{d y}{d x}+\alpha y=x e^{\beta x}$
$d\left(e^{\alpha x} \cdot y\right) x e^{\alpha x} \cdot e^{\beta x}$
$d\left(e^{\alpha x} \cdot y\right)=x e^{(\alpha+\beta) x}$ ... (i)
Case-I : $\alpha+\beta \neq 0$
$d \left( e ^{\alpha x} \cdot y \right)= xe ^{(\alpha+\beta) x}$
$e ^{\alpha x} \cdot y =\frac{ xe ^{(\alpha+\beta) x}}{(\alpha+\beta)}-\frac{ e ^{(\alpha+\beta) x}}{(\alpha+\beta)^{2}}+ C$
$y =\frac{ xe ^{\beta x}}{(\alpha+\beta)}-\frac{ e ^{\beta x}}{(\alpha+\beta)^{2}}+ Ce ^{-\alpha x}$
$\alpha=1, \beta=1 \Rightarrow y =\frac{ xe ^{x}}{2}-\frac{ e ^{x}}{4}+ Ce ^{- x }$
as $y (1)=1 \Rightarrow C = e \left(1-\frac{ e }{4}\right)$
$y ( x )=\frac{x e ^{x}}{2}-\frac{ e ^{x}}{4}+\left( e -\frac{ e ^{2}}{4}\right) e ^{- x }$
Case-II : $\alpha+\beta=0$
$\Rightarrow \frac{d y}{d x}-\beta y=x e^{\beta x}$
$d\left(e^{-\beta x} y\right)=x$
$e^{-\beta x} \cdot y=\frac{x^{2}}{2}+C$
$y=\frac{e^{\beta x} x^{2}}{2}+C e^{\beta x}$
$y(1)=1$
$\Rightarrow C=\left(1-\frac{e}{2}\right) \frac{1}{e} $
$\Rightarrow y=e^{\beta x} \cdot \frac{x^{2}}{2}+\left(1-\frac{e}{2}\right) \frac{1}{e} \cdot e^{\beta x}$
Take $\beta=-1$
$ \Rightarrow y=\frac{x^{2}}{2} e^{-x}+\left(1-\frac{e}{2}\right) e^{-x}$

Q5. Let $O$ be the origin and $\overrightarrow{ OA }=2 \hat{ i }+2 \hat{ j }+\hat{ k }, \overrightarrow{ OB }=\hat{ i }-2 \hat{ j }+2 \hat{ k }$ and $\overrightarrow{ OC }=\frac{1}{2}(\overrightarrow{ OB }-\lambda \overrightarrow{ OA })$ for some $\lambda > 0$. If $|\overrightarrow{ OB } \times \overrightarrow{ OC }|=\frac{9}{2}$, then which of the following statements is(are) TRUE?

A

Projection of $\overrightarrow{ OC }$ on $\overrightarrow{ OA }$ is $-\frac{3}{2}$

B

Area of the triangle $OAB$ is $\frac{9}{2}$

C

Area of the triangle $ABC$ is $\frac{9}{2}$

D

The acute angle between the diagonals of the parallelogram with adjacent sides $\overrightarrow{ OA }$ and $\overrightarrow{ OC }$ is $\frac{\pi}{3}$

Solution

image
$\overrightarrow{ OA } \cdot \overrightarrow{ OB }=0 \Rightarrow \overrightarrow{ OA } \perp \overrightarrow{ OB }$
$\overrightarrow{ OC }=\frac{1}{2}((1-2 \lambda) \hat{ i }+(-2-2 \lambda) \hat{ j }+(2-\lambda) \hat{ k })$
$|\overrightarrow{ OB } \times \overrightarrow{ OC }|=\frac{9|\lambda|}{2}=\frac{9}{2} $
$\Rightarrow \lambda=\pm 1, $ as $ \lambda>0, \lambda=1 $
$\overrightarrow{ OC }=\frac{\overrightarrow{ OB }-\overrightarrow{ OA }}{2}$
(A) Projection $\overrightarrow{ OC }$ on $\overrightarrow{ OA }$
$\overrightarrow{ OC } \cdot \widehat{ OA }=-\frac{3}{2}$
(B) Area of $\triangle OAB =9 / 2$
(C) Area of $\triangle ABC =9 / 2$
(D) $\overrightarrow{ OA }+\overrightarrow{ OC }=\frac{3 \hat{i}+3 \hat{x}}{2}$,
$ \overrightarrow{ OA }-\overrightarrow{ OC }=\frac{5 \hat{i}+8 \hat{j}+\hat{k}}{2}$
$(\overrightarrow{ OA }+\overrightarrow{ OC })(\overrightarrow{ OA }-\overrightarrow{ OC })=|\overrightarrow{ OA }+\overrightarrow{ OC }||\overrightarrow{ OA }-\overrightarrow{ OC }| \cos \theta $
$\cos \theta=\frac{1}{\sqrt{5}}$

Q6. Let $E$ denote the parabola $y ^{2}=8 x$. Let $P =(-2,4)$ and let $Q$ and $Q ^{\prime}$ be two distinct points on $E$ such that the lines $P Q$ and $P Q^{\prime}$ are tangents to $E$. Let $F$ be the focus of $E$. Then which of the following statements is(are) TRUE?

A

The triangle $PFQ$ is a right-angled triangle

B

The triangle $QPQ '$ is a right-angle triangle

C

The distance between $P$ and $F$ is $5 \sqrt{2}$

D

$F$ lies on the line joining $Q$ and $Q'$

Solution

image
$ E = y ^{2}-8 x =0 $
$ a =2$
Let $ Q \left(2 t _{1}^{2}, 4 t _{1}\right), Q '\left(2 t _{2}^{2}, 4 t _{2}\right)$
$ t _{1} t _{2}=-1, t _{1}+ t _{2}=2 $
$ t _{1}=1+\sqrt{2}, t _{2}=1-\sqrt{2}$
(A) ( slope of $PF$)( slope of $FQ)=-1$
$\Rightarrow \angle PFQ =\frac{\pi}{2}$
(B) ( slope of $PQ')($ slope of $PQ )=-1$
$\angle QPQ'=\frac{\pi}{2}$
(C) $PF =4 \sqrt{2}$
(D) slope of $Q' F =$ slope of $FQ$
$\Rightarrow Q , F , Q'$ are collinear

Q7. Consider the region $R=\left\{(x, y) \in R \times R: x \geq 0\right.$ and $\left.y^{2} \leq 4-x\right\}$. Let $F$ be the family of all circles that are contained in $R$ and have centers on the $x$-axis. Let $C$ be the circle that has largest radius among the circles in $F$. Let $(\alpha, \beta)$ be a point where the circle $C$ meets the curve $y ^{2}=4- x$.
The radius of the circle $C$ is _____

Answer: 1.5

Solution

Let the equation of circle $(x-r)^{2}+y^{2}=r^{2}$
Equation of parabola $y^{2}=4-x$
Solving them
$(x-r)^{2}+4-x=r^{2} $
$\Rightarrow x^{2}-x(2 r+1)+4=0$
Since circle and parabola meet tangentially hence
$(2 r+1)^{2}-16=0 $
$\Rightarrow 2 r+1=4 $
$\Rightarrow r=3 / 2 $ and $ x^{2}-4 x+4=0$
$(x-2)^{2}=0 $
$\Rightarrow \alpha=2, r=3 / 2=1.5$

Q8. Consider the region $R=\left\{(x, y) \in R \times R: x \geq 0\right.$ and $\left.y^{2} \leq 4-x\right\}$. Let $F$ be the family of all circles that are contained in $R$ and have centers on the $x$-axis. Let $C$ be the circle that has largest radius among the circles in $F$. Let $(\alpha, \beta)$ be a point where the circle $C$ meets the curve $y ^{2}=4- x$.
The value of $\alpha$ is ____

Answer: 2

Solution

Let the equation of circle $(x-r)^{2}+y^{2}=r^{2}$
Equation of parabola $y^{2}=4-x$
Solving them
$(x-r)^{2}+4-x=r^{2} $
$\Rightarrow x^{2}-x(2 r+1)+4=0$
Since circle and parabola meet tangentially hence
$(2 r+1)^{2}-16=0 $
$\Rightarrow 2 r+1=4 $
$\Rightarrow r=3 / 2 $ and $ x^{2}-4 x+4=0$
$(x-2)^{2}=0 $
$\Rightarrow \alpha=2, r=3 / 2=1.5$

Q9. Let $f_{1}:(0, \infty) \rightarrow R$ and $f_{2}:(0, \infty) \rightarrow R$ be defined by $f_{1}(x)=\int\limits_{0}^{x} \displaystyle\prod_{j=1}^{21}(t-j)^{j} d t, x>0$ and $f _{2}( x )=98( x -1)^{50}-600( x -1)^{49}+2450, x >0$, where, for any positive integer $n$ and real numbers $a _{1}, a _{2}$, $\ldots . ., a_{n}, \displaystyle\prod_{i=1}^{n} a_{i}$ denotes the product of $a_{1}, a_{2}, \ldots ., a_{n} .$ Let $m_{i}$ and $n_{i}$, respectively, denote the number of points of local minima and the number of points of local maxima of function $f _{ i }, i =1,2$, in the interval $(0$, $\infty$ ).
The value of $2 m_{1}+3 n_{1}+m_{1} n_{1}$ is _____

Answer: 57

Solution

$f_{1}(x)=\int\limits_{0}^{x} \displaystyle\prod_{j=1}^{21}(t-j)^{j} d t$
$\Rightarrow f_{1}^{\prime}(x)=\displaystyle\prod_{j=1}^{21}(x-j)^{j}$
Therefore $m_{1}=6, n_{1}=5$
$ 2 m_{1} +3 n_{1}+m_{1} n_{1} $
$=2(6)+3(5)+30 $
$=12+15+30=57$

Q10. Let $f_{1}:(0, \infty) \rightarrow R$ and $f_{2}:(0, \infty) \rightarrow R$ be defined by $f_{1}(x)=\int\limits_{0}^{x} \displaystyle\prod_{j=1}^{21}(t-j)^{j} d t, x>0$ and $f _{2}( x )=98( x -1)^{50}-600( x -1)^{49}+2450, x >0$, where, for any positive integer $n$ and real numbers $a _{1}, a _{2}$, $\ldots . ., a_{n}, \displaystyle\prod_{i=1}^{n} a_{i}$ denotes the product of $a_{1}, a_{2}, \ldots ., a_{n} .$ Let $m_{i}$ and $n_{i}$, respectively, denote the number of points of local minima and the number of points of local maxima of function $f _{ i }, i =1,2$, in the interval $(0$, $\infty$ ).
The value of $6 m_{2}+4 n_{2}+8 m_{2} n_{2}$ is _____

Answer: 6

Solution

$f _{2}^{\prime}( x )=(98)(50)( x -1)^{49}-(600)(49)( x -1)^{48}$
$=(49)(100)( x -1)^{48}( x -1-6)$
$m _{2}=1, n _{2}=0$
$6 m _{2}+4 n _{2}+8 m _{2} n _{2}$
$6(1)+4(0)+8(0)=6$

Q11. Let $g _{ i }:\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] \rightarrow R , i =1,2$ and $f :\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] \rightarrow R$ be functions such that $g_{1}(x)=1, g_{2}(x)=|4 x-\pi|$ and $f(x)=\sin ^{2} x$, for all $x \in\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] .$ Define $S_{i}=\int\limits_{\frac{\pi}{8}}^{\frac{3 \pi}{8}} f(x) \cdot g_{i}(x) d x, i=1,2$
The value of $\frac{16 S _{1}}{\pi}$ is_____

Answer: 2

Solution

$g _{1}:\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] \rightarrow R , i =1,2, f :\left[\frac{\pi}{ r }, \frac{3 \pi}{ r }\right] \rightarrow R$
$g _{1}=1, g _{2}=|4 x -\pi|, f ( x )=\sin ^{2} x$
$S _{1}=\int\limits_{\pi / 8}^{3 / 8} f ( x ) \cdot g _{1}( x ) d x$
$S _{1}=\int\limits_{\pi / 8}^{3 \pi / 8} \sin ^{2} x dx =\int\limits_{\pi / 8}^{3 \pi / 8} \sin ^{2}\left(\frac{\pi}{2}- x \right) dx $
$\Rightarrow 2 S _{1}=\int\limits_{\pi / 8}^{3 \pi / 8} 1 dx$
$\Rightarrow S _{1}=\frac{1}{2}\left(\frac{3 \pi}{8}-\frac{\pi}{8}\right)=\frac{\pi}{8} $
$\Rightarrow \frac{16 S _{1}}{\pi}=2$

Q12. Let $g _{ i }:\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] \rightarrow R , i =1,2$ and $f :\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] \rightarrow R$ be functions such that $g_{1}(x)=1, g_{2}(x)=|4 x-\pi|$ and $f(x)=\sin ^{2} x$, for all $x \in\left[\frac{\pi}{8}, \frac{3 \pi}{8}\right] .$ Define $S_{i}=\int\limits_{\frac{\pi}{8}}^{\frac{3 \pi}{8}} f(x) \cdot g_{i}(x) d x, i=1,2$
The value of $\frac{48 \,S _{2}}{\pi^{2}}$ is_____

Answer: 1.5

Solution

$S _{2}=\int\limits_{\pi / 8}^{3 \pi / 8} \sin ^{2} x |4 x -\pi| dx $
$=\int\limits_{\pi / 8}^{3 \pi / 8} \sin ^{2}\left(\frac{\pi}{2}- x \right)\left|4\left(\frac{\pi}{2}- x \right)-\pi\right| dx$
$=\int\limits_{\pi / 8}^{3 \pi / 8} \cos ^{2} x |4 x -\pi| dx$
$\Rightarrow 2 S _{2}=\int\limits_{\pi / 8}^{3 \pi / 8}|4 x -\pi| dx $
$=2 \int\limits_{\pi / 8}^{\pi / 4}(\pi-4 x ) dx$
$S _{2}=\left.\left(\pi x -2 x ^{2}\right)\right|_{\pi / 8} ^{\pi / 4}$
$=\pi\left(\frac{\pi}{4}-\frac{\pi}{8}\right)-2\left(\frac{\pi^{2}}{16}-\frac{\pi^{2}}{64}\right)$
$S _{2}=\frac{4 \pi^{2}}{8}-\frac{3 \pi^{2}}{32}=\frac{\pi^{2}}{32}$
$=\frac{48 S _{2}}{\pi^{2}}=\frac{48}{\pi^{2}} \times \frac{\pi^{2}}{32}=\frac{3}{2}$
$\frac{48 S _{2}}{\pi^{2}}=1.5$

Q13. Let $M=\left\{(x, y) \in R \times R: x^{2}+y^{2} \leq r^{2}\right\}$, where $r>0$. Consider the geometric progression $a_{n}=\frac{1}{2^{n-1}}, n=1,2,3, \ldots .$ Let $S_{0}=0$ and for $n \geq 1$, let $S_{n}$ denote the sum of the first $n$ terms of this progression. For $n \geq 1$, let $C_{n}$ denote the circle with center $\left(S_{n-1}, 0\right)$ and radius $a_{n}$, and $D_{n}$ denote the circle with center $\left(S_{n-1}, S_{n-1}\right)$ and radius $a_{n}$.
Consider $M$ with $r=\frac{1025}{513}$. Let $k$ be the number of all those circles $C_{n}$ that are inside $M$. Let $1$ be the maximum possible number of circles among these $k$ circles such that no two circles intersect. Then

A

$k+2 l=22$

B

$2 k +1=26$

C

$2 k +3 l =34$

D

$3 k +2 l =40$

Solution

image
$C _{1} \rightarrow(0,0), r =1$
$C _{2} \rightarrow(1,0), r =1 / 2$
$C _{3} \rightarrow(3 / 2,0), r =1 / 4$
$\vdots$
$C_{n}\left(2\left(1-\frac{1}{2^{n-1}}\right), 0\right), r=\frac{1}{2^{n-1}}$
$\Rightarrow 2\left(1-\frac{1}{2^{n-1}}\right)+\frac{1}{2^{n-1}} < r$
$ 2-\frac{1}{2^{n-1}} < r$
$\Rightarrow 2-\frac{1}{2^{n-1}} < \frac{1025}{513}$
$\Rightarrow \frac{1}{2^{n-1}}>\frac{1}{513}$
$\Rightarrow 2^{n-1} < 513 $
$\Rightarrow n-1 \leq 9$
$\Rightarrow n \leq 10 \Rightarrow k=10$
Also no two by $C _{1}, C _{3}, C _{5}, C _{7}, C _{9}$ intersect each other.
And no two of $C _{2}, C _{4}, C _{6}, C _{8}, C _{10}$ intersect each other
For both, we get $1=5$
$\Rightarrow 3 k +2 l =40$

Q14. Let $M=\left\{(x, y) \in R \times R: x^{2}+y^{2} \leq r^{2}\right\}$, where $r>0$. Consider the geometric progression $a_{n}=\frac{1}{2^{n-1}}, n=1,2,3, \ldots .$ Let $S_{0}=0$ and for $n \geq 1$, let $S_{n}$ denote the sum of the first $n$ terms of this progression. For $n \geq 1$, let $C_{n}$ denote the circle with center $\left(S_{n-1}, 0\right)$ and radius $a_{n}$, and $D_{n}$ denote the circle with center $\left(S_{n-1}, S_{n-1}\right)$ and radius $a_{n}$.
Consider $M$ with $r=\frac{\left(2^{199}-1\right) \sqrt{2}}{2^{198}}$. The number of all those circles $D_{n}$ that are inside $M$ is

A

198

B

199

C

200

D

201

Solution

image
$\sqrt{2} S_{n-1}+a_{n} < r$
$\Rightarrow \sqrt{2}\left(2\left(1-\frac{1}{2^{n-1}}\right)\right)+\frac{1}{2^{n-1}} < \left(\frac{2^{199}-1}{2^{198}}\right) \sqrt{2}$
$\Rightarrow \sqrt{2}\left(1-\frac{1}{2^{n-1}}\right)+\frac{1}{2^{n}} < \left(1-\frac{1}{2^{199}}\right) \sqrt{2}$
$\Rightarrow \frac{1}{(\sqrt{2})^{2 n}}-\frac{1}{(\sqrt{2})^{2 n-3}} < \frac{-1}{(\sqrt{2})^{397}}$
$\Rightarrow \frac{2 \sqrt{2}-1}{(\sqrt{2})^{2 n}}>\frac{1}{(\sqrt{2})^{397}}$
$\Rightarrow (\sqrt{2})^{2 n-397} < 2 \sqrt{2}-1$
$\Rightarrow 2 n-397 \leq 1 \Rightarrow n \leq 199$

Q15. Let $\Psi_{1}:[0, \infty) \rightarrow R, \Psi_{2}:[0, \infty) \rightarrow R, f:[0, \infty) \rightarrow R$ and $g:[0, \infty) \rightarrow R$ be functions such that $f (0)= g (0)=0$,
$\psi_{1}(x)=e^{-x}+x, x \geq 0, $
$\psi_{2}(x)=x^{2}-2 x-2 e^{-x}+2, x \geq 0,$
$f(x)=\int\limits_{-x}^{x}\left(|t|-t^{2}\right) e^{-t^{2}} d t, x > 0$
and $g(x)=\int\limits_{0}^{x^{2}} \sqrt{t} e^{-t} d t, x>0$.
Which of the following statements is TRUE?

A

$f(\sqrt{\ln 3})+g(\sqrt{\ln 3})=\frac{1}{3}$

B

For every $x > 1$, there exists and $\alpha \in(1, x)$ such that $\psi_{1}(x)=1+\alpha x$

C

For every $x > 0$, there exists a $\beta \in(0, x)$ such that $\psi_{2}(x)=2 x\left(\psi_{1}(\beta)-1\right)$

D

$f$ is an increasing function on the interval $\left[0, \frac{3}{2}\right]$

Solution

$\psi_{2}( x )= x ^{2}-2 x -2 e ^{- x }+2, x \geq 0$
$\psi_{2}^{\prime}( x )=2 x -2+2 e ^{- x }=2\left( x + e ^{- x }-1\right) $
$\psi_{2}^{\prime}(\beta)=2\left(\psi_{1}(\beta)-1\right)$
Since $\psi_{2}(x)$ is a continuous and differentiable function $\forall x \in[0, x]$
$\psi_{2}(0)=0, \psi_{2}(x)=x^{2}-2 x-2 e^{-x}+2$
Hence according to LMVT there exist at least one $\beta \in(0, x)$ such that
$\left(\frac{\psi_{2}( x )-\psi_{2}(0)}{ x }\right)=\psi_{2}^{\prime}(\beta)$
$=\frac{\psi_{2}( x )}{ x }=2\left(\psi_{1}(\beta)-1\right)$
$=\psi_{2}( x )=2 x \left(\psi_{1}(\beta)-1\right)$

Q16. Let $\Psi_{1}:[0, \infty) \rightarrow R, \Psi_{2}:[0, \infty) \rightarrow R, f:[0, \infty) \rightarrow R$ and $g:[0, \infty) \rightarrow R$ be functions such that $f (0)= g (0)=0$,
$\psi_{1}(x)=e^{-x}+x, x \geq 0, $
$\psi_{2}(x)=x^{2}-2 x-2 e^{-x}+2, x \geq 0,$
$f(x)=\int\limits_{-x}^{x}\left(|t|-t^{2}\right) e^{-t^{2}} d t, x > 0$
and $g(x)=\int\limits_{0}^{x^{2}} \sqrt{t} e^{-t} d t, x>0$.
Which of the following statements is TRUE?

A

$\psi_{1}( x ) \leq 1$, for all $x >0$

B

$\psi_{2}( x ) \leq 0$, for all $x >0$

C

$f(x) \geq 1-e^{-x^{2}}-\frac{2}{3} x^{3}+\frac{2}{5} x^{5}$, for all $x \in\left(0, \frac{1}{2}\right)$

D

$g(x) \leq \frac{2}{3} x^{3}-\frac{2}{5} x^{5}+\frac{1}{7} x^{7}$, for all $x \in\left(0, \frac{1}{2}\right)$

Solution

$\psi^{\prime}{ }_{1}( x )=1- e ^{- x }>0$
$\psi_{2}( x )=( x -1)^{2}+1-2 e ^{- x }>0$ for $x =1$
$\because e ^{- t }=1- t +\frac{ t ^{2}}{2}-\frac{ t ^{3}}{3}+\ldots$
$ \sqrt{ t } e ^{- t }=\sqrt{ t }- t ^{3 / 2}+\frac{1}{2} t ^{5 / 2} \ldots$
So, $ \sqrt{ t } e ^{- t }<\sqrt{ t }- t ^{3 / 2}+\frac{1}{2} t ^{5 / 2}$ for $t \in(0,1)$
$ \int\limits_{0}^{ x ^{2}} \sqrt{ t } e ^{- t } dt < \int\limits_{0}^{ x ^{2}}\left(\sqrt{ t }- t ^{3 / 2}+\frac{1}{2} t ^{5 / 2}\right) dt$
$=\frac{2}{3} x ^{3}-\frac{2}{5} x ^{5}+\frac{1}{7} x ^{7}$

Q17. A number is chosen at random from the set $\{1,2,3, \ldots . ., 2000\} .$ Let $p$ be the probability that the chosen number is a multiple of $3$ or a multiple of $7$ . Then the value of $500\, p$ is_____

Answer: 214

Solution

Let $A =\{1,2,3, \ldots ., 2000\}$
Let $E _{1}=3 m , 1 \leq m \leq 666, m \in N$
$ E _{2}=7 k , 1 \leq k \leq 285, k \in N$
$= n \left( E _{1} \cup E _{2}\right)=666+285-95=856$
$= P \left( E _{1} \cup E _{2}\right)=856 / 2000$
$=500 \beta=856 / 4=214$

Q18. Let $E$ be the ellipse $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$. For any three distinct points $P, Q$ and $Q'$ on $E$, let $M(P, Q)$ be the midpoint of the line segment joining $P$ and $Q$, and $M \left( P , Q '\right)$ be the mid-point of the line segment joining $P$ and $Q'$. Then the maximum possible value of the distance between $M ( P , Q )$ and $M \left( P , Q '\right)$, as $P , Q$ and $Q'$ vary on $E$, is _____

Answer: 4

Solution

$M ( P , Q )$ is mid-point of $PQ$
$M \left( P , Q'\right)$ is mid-point of $PQ ^{\prime}$
In a $\triangle PQQ'$ since $M ( P , Q ) \& M \left( P , Q '\right)$ are mid-point
of $PQ \& PQ'$ hence line joining M(P,Q), M(P,Q') is
parallel to $QQ'$ and half of it.
$\Rightarrow \max$ distance $=\frac{1}{2} Q Q'=\frac{1}{2}(8)=4$

Q19. For any real number $x$, let $[x]$ denote the largest integer less than or equal to $x$. If
$I=\int\limits_{0}^{10}\left[\sqrt{\frac{10 x}{x+1}}\right] d x,$
then the value of $9I$ is _____

Answer: 182

Solution

$ I=\int\limits_{0}^{10}\left[\sqrt{\frac{10 x}{x+1}}\right] d x$
$\left[\sqrt{\frac{10 x}{x+1}}\right]=n $
$\Rightarrow \frac{n^{2}}{10-n^{2}} \leq x < \frac{(n+1)^{2}}{10-(n+1)^{2}}$ where $n \in I$
For $n=0,0 \leq x < 1 / 9$
$n=1 ; 1 / 9 \leq x < 2 / 3 $
$ n=2 ; 2 / 3 \leq x < 9, n=3, x \geq 9$
$ I=\int\limits_{0}^{1 / 9} 0 \cdot d x+\int\limits_{1 / 9}^{2 / 3} 1 \cdot d x+\int\limits_{2 / 3}^{9} 2 \cdot d x+\int\limits_{9}^{10} 3 \cdot d x $
$=\left(\frac{2}{3}-\frac{1}{9}\right)+2\left(9-\frac{2}{3}\right)+3(10-9)$
$=\frac{182}{9}=9 I=182$