JEE Main Physics Question Paper with Solution 2023 January 31st Shift 1 - Morning
A
$8.8 \times 10^{-5} J$
B
$7.92 \times 10^{-4} J$
C
$7.92 \times 10^{-6} J$
D
$9.68 \times 10^{-4} J$
Solution
$ 1000 \times \frac{4 \pi}{3}(1)^3=\frac{4 \pi}{3} R^3 $
$R=10 \,mm$
$ T \times 1000 \times 4 \pi\left(10^{-3}\right)^2- T \times 4 \pi\left(10 \times 10^{-3}\right)^2=\Delta E$
$ \Delta E =4 \times \pi \times 7 \times 10^{-2}[1000-100] \times 10^{-6} $
$\Delta E =7.92 \times 10^{-4} J$
A
$4800 \, km$
B
$640 \, km$
C
$2560\, km$
D
$5260\, km$
Solution
$ \frac{ GM }{ R ^2}\left[1-\frac{ d }{ R }\right]=\frac{4 \times GM }{(4 R )^2}$
$ 1-\frac{ d }{ R }=\frac{1}{4} \Rightarrow \frac{ d }{ R }=\frac{3}{4} \Rightarrow d \frac{3}{4} R $
$ d =4800\, km $
A
$125$
B
$12.5$
C
$\frac{5}{16}$
D
$\frac{32}{5}$
Solution
$\phi=\mu_{ r } \mu_0 \frac{ N }{\ell} I \times A$
$ \mu_{ r }=125$
A
$\frac{I_0}{8}$
B
ZerO
C
$\frac{I_0}{2}$
D
$\frac{I_0}{4}$
Solution
$ I_A=\frac{I_o}{2} $
$ I C=\frac{I_o}{2} \cos ^2 45=\frac{I_o}{4} $
$ I_B=I_C \cos ^2 45=\frac{I_o}{8}$
A
A is correct but $R$ is not correct
B
Both $A$ and $R$ are correct but $R$ is Not the correct explanation of $A$
C
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
D
A is not correct but $R$ is correct
A
$\frac{100 m v}{t}$
B
$200 m v t$
C
$\frac{200 m v}{t}$
D
$\frac{m v}{100 t}$
Solution
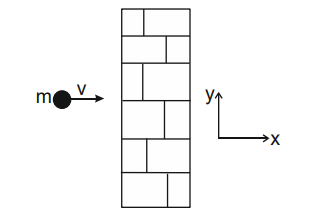
$P _{ i }= Nm \cup \hat{ i } \,\,\,\, \vec{ P }_{ f }=- Nm v \hat{ i }$
$N$ is Number of balls strikes with wall
$ N =100$
$ \Delta \vec{ P }=\vec{ P }_{ f }-\vec{ P }_{ i }=-2 Nm v \hat{ i }$
$=-200 Nm \hat{\hat{i}} $
$\vec{ F }_{\text {Total }}=\frac{\Delta \vec{ P }}{\Delta t }=-\frac{200 mvt }{ t } $
$ |\vec{ F }|=\frac{200 mv }{ t }$
A
$4.5\, J$
B
$-4.5 \,J$
C
zero
D
$6 \,J$
Solution
As $\Delta q =0$
$ \Delta u =- W $
$ W =\int PdV$
$ \Delta u =- W =30 \times 10^3 \times 150 \times 10^{-6}$
$ =4500 \times 10^{-3}$
$=4.5\, J $
A
$\gamma \alpha T ^{\circ}$
B
$\gamma \alpha \frac{1}{T}$
C
$\gamma \alpha T$
D
$\gamma \alpha \frac{1}{\sqrt{T}}$
Solution
$\gamma$ is independent of temperature
Q9. A free neutron decays into a proton but a free proton does not decay into neutron. This is because
A
neutron is an uncharged particle
B
neutron has larger rest mass than proton
C
neutron is a composite particle made of a proton and an electron
D
proton is a charged particle
Solution
As neutron has more rest mass than proton it will require energy to decay proton into neutron. Option 4
A
$\frac{V_{ d }}{4}$
B
$\frac{ V _{ d }}{2}$
C
$2 V _{ d }$
D
$V _{ d }$
Solution
$V_d=\frac{e E}{m} \tau$ that is independent of area
A
Both will reach the earth's surface simultaneously.
B
Insulating ball will reach the earth's surface earlier than the metal ball
C
Metal ball will reach the earth's surface earlier than the insulating ball
D
Time taken by them to reach the earth's surface will be independent of the properties of their materials
Solution
When metal is passing through magnetic field, eddy current will produce and it will oppose the motion, so it will take more time
A
$R X_L \quad X_C$
B
$\frac{R}{\sqrt{X_L X_C}}$
C
$\frac{R}{X_L X_C}$
D
$R \frac{X_L}{X_C}$
Solution
All three have same dimension therefore $\frac{R}{\sqrt{X_L X_C}}$ is dimensionless.
A
B Only
B
A and B Only
C
A, D and E Only
D
A Only
Solution
Carrier wave frequency
$V _{ C }=\frac{100 \pi}{2 \pi}=500 \,Hz$
Modulating wave frequency
$ V _{ m }=\frac{4 \pi}{2 \pi}=2\, Hz$
$\therefore V _{ C }- V _{ m }, V _{ c }, V _{ c }+ V _{ m }$
$=498\, Hz , 500\, Hz , 502 \,Hz$
A
$4 \,J$
B
$1\, J$
C
$2\, J$
D
ZeIO
Solution
$ u=-M B \cos \theta $
$ W=\Delta u $
$ W=-M B \cos 180^{\circ}\left(-m B \cos 0^{\circ}\right) $
$ W=2 M B=2 \times 5 \times 0.4=4\, J$
A
Micro waves
B
Gamma rays
C
Radio waves
D
Ultraviolet rays
Solution
$ \text { Energy of one photon }=\frac{\text { Power }}{\text { Photon frequency }} $
$ E=h v=\frac{15 \times 10^3}{10^{16}} $
$ v=\frac{15 \times 10^{-13}}{6 \times 10^{-34}}=2.5 \times 10^{21}$
So gamma Rays. Option 3
A
$18.75\, J$
B
$37.5\, J$
C
$9.75 \,J$
D
$12.5\, J$
Solution
$u _{\max }=\frac{1}{2} m \omega^2 A ^2=25 J$
$KE$ at $\frac{ A }{2}=\frac{1}{2} m v_1^2=\frac{1}{2} m \omega^2\left(A^2-\frac{A^2}{4}\right)$
$KE =\frac{1}{2} m \omega^2 \frac{3 A ^2}{4}=\frac{3}{4}\left(\frac{1}{2} m ^2 A ^2\right) $
$KE =\frac{3}{4} \times 25=18.75\, J$
A
$800 N$
B
$600 N$
C
$200 \sqrt{3} N$
D
$800 \sqrt{2} N$
Solution
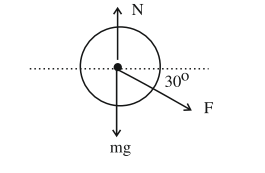
$ N = mg + F \sin 30^{\circ} $
$ =700+200 \times \frac{1}{2}=800$ newton.
A
$\frac{2 u }{ g }$
B
$\frac{ u }{2 g }$
C
$\frac{ u }{ g }$
D
$\frac{\sqrt{3} u}{g}$
Solution
$ u \cos \theta=\frac{\sqrt{3} u }{2} $
$\Rightarrow \cos \theta=\frac{\sqrt{3}}{2}$
$\Rightarrow \theta=30^{\circ} $
$ T =\frac{2 u \sin 30^{\circ}}{ g }=\frac{ u }{ g }$
A
$n _{ e }$ decreases, resistance increases
B
Both $n _{ e }$ and resistance increase
C
$n _{ e }$ increases, resistance decreases
D
Both $n_e$ and resistance decrease
Solution
As temperature increases, more electron excite to conduction band and hence conductivity increases, therefore resistance decreases.
Answer: 20
Solution

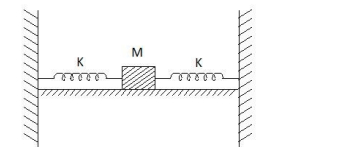
Keff $= K + K$ as both springs are in use in parallel
$=2 k $
$=2 \times 2=4 N / m $
$m =490 \,gm $
$ =0.49 \,kg$
$T =2 \pi \sqrt{\frac{ m }{ Keff }}=2 \pi \sqrt{\frac{0.49 kg }{4}} $
$ =2 \pi \sqrt{\frac{49}{400}}=2 \pi \frac{7}{20}=\frac{7 \pi}{10}$
No. of oscillation in the $14 \pi$ is
$N =\frac{\text { time }}{ T }=\frac{14 \pi}{7 \pi / 10}=20$
Answer: 10
Solution
$ \frac{1}{2} mv ^2+\frac{1}{2} I \omega^2=7 \times 10^{-3}$
$ \frac{1}{2} mv ^2+\frac{1}{2}\left(\frac{2}{5} MR ^2\right)\left(\frac{ V }{ R }\right)^2=7 \times 10^{-3} $
$ \frac{1}{2} MV ^2\left[1+\frac{2}{5}\right]=7 \times 10^{-3} $
$ \frac{1}{2}(1)\left( V ^2\right)\left(\frac{7}{5}\right)=7 \times 10^{-3}$
$ V ^2=10^{-2} $
$ V =10^{-1}=0.1\, m / s =10 \,cm / s$
Answer: 640
Solution
Flux $ =\vec{ E } \cdot \vec{ A } $
$ =4000(0 \cdot 2)^2 \frac{ V }{ m } \cdot(0 \cdot 2)^2 m ^2$
$ =4000 \times 16 \times 10^{-4} Vm $
$ =640 \,Vcm $
Answer: 5
Solution
$V =\frac{ C }{\mu} \Rightarrow \mu=\frac{ C }{ V }=\frac{ C }{0.2 C } $
$ \mu=5 $
$ \mu=\sqrt{\epsilon_{ r } \mu_{ r }}$
$ \Rightarrow \epsilon_{ r }=\frac{\mu^2}{\mu_{ r }} $
$ \therefore \frac{\epsilon_{ r }}{\mu}=\frac{\mu}{\mu_{ r }}=5$
Answer: 3
Solution

time to cross the River width $\omega=1000 \,m$
$\text { is }=\frac{1 km }{4 km / h }$
Drift $x=V m / g \times t$
Where $Vm / g$ is velocity of River w.r. to ground.
$ x = Vm / g \times \frac{1}{4}=750 m =\frac{3}{4} km$
$ Vm / g =3 \,km / hr$
Answer: 7
Solution
$ v ^2 = u ^2+2 as $
$ =2^2+2(2)(6) $
$ =4+24=28$
$KE =\frac{1}{2} mv ^2 $
$ =\frac{1}{2}(500) 28 $
$ =7000 \,J $
$ =7\, kJ $
Answer: 27
Solution
$ \frac{1}{\lambda}= Rz ^2\left[\frac{1}{ n _1^2}-\frac{1}{ n _2^2}\right]$
$\frac{1}{\lambda_1}= Rz ^2\left[\frac{1}{1^2}-\frac{1}{3^2}\right]=\frac{8}{9} Rz ^2 $.....(1)
$ \frac{1}{\lambda_2}= Rz ^2\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3}{4} Rz ^2$......(2)
$1 / 2 \Rightarrow \frac{\lambda_2}{\lambda_1}=\frac{8}{9} \times \frac{4}{3}=\frac{32}{27} $
$\frac{\lambda_1}{\lambda_2}=\frac{27}{32}$
$=27$
Answer: 242
Solution
$X_L=X_C$
So, $Z=R=20 \Omega$
$ i _{ rms }=\frac{220}{20}=11 $
$ i _{\max }=11 \sqrt{2}=\sqrt{242}$
Answer: 60
Solution
If $\Delta \ell$ is decease in length of rod due to decease in temperature

$\Delta \ell=\ell \alpha \Delta T $
$ \alpha=2 \times 10^{-5} K ^{-1}, \Delta T =(210-160) $
$ =50 K $
$ \Delta \ell=1 \times 2 \times 10^{-5} \times 50=10^{-3} m $
$\text { Young Modulus }= Y =\frac{ F / A }{\Delta \ell / \ell} A =3 \times 10^{-6} m ^2 $
$2 \times 10^{11}=\frac{ Mg / 3 \times 10^{-6}}{10^{-3} / 1} $
$Mg =2 \times 10^{11} \times 3 \times 10^{-9}=6 \times 10^{-2}$
$ M=60\, kg $
Answer: 5
Solution

$i =\frac{2 \varepsilon}{5+2 r }\ldots$(1)
$ i=\frac{\varepsilon}{\frac{r}{2}+5} \ldots$ (2)
Equating (1) and (2)
$\frac{2 \varepsilon}{5+2 r }=\frac{\varepsilon}{\frac{ r }{2}+5} $
$\Rightarrow r +10=5+2 r$
$r =5$
JEE Main Chemistry Question Paper with Solution 2023 January 31st Shift 1 - Morning
A
B
C
D
Solution
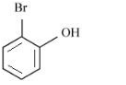
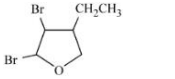
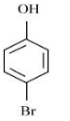
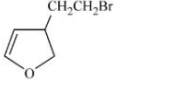
Aromatic compounds burns with sooty flame
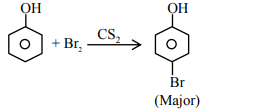
A
$n =1$ to $n =3$
B
$n =1$ to $n =2$
C
$n =2$ to $n =1$
D
$n =3$ to $n =4$
Solution
$He ^{+}$ion :
$\frac{1}{\lambda( H )}= R (1)^2\left[\frac{1}{ n _1^2}-\frac{1}{ n _2^2}\right] $
$ \frac{1}{\lambda\left( He ^{+}\right)}= R (2)^2\left[\frac{1}{2^2}-\frac{1}{4^2}\right]$
Given $\lambda( H )=\lambda\left( He ^{+}\right)$
$ R (1)^2\left[\frac{1}{ n _1^2}-\frac{1}{ n _2^2}\right]= R (4)\left[\frac{1}{2^2}-\frac{1}{4^2}\right] $
$ \frac{1}{ n _1^2}-\frac{1}{ n _2^2}=\frac{1}{1^2}-\frac{1}{2^2}$
On comparing $n _1=1 \& n _2=2$
A
$Br _2$, alc $\cdot KOH , NaNH _2, Na \left( Liq NH _3\right)$
B
$Br _2$, alc $\cdot KOH , NaNH _2, H _2$ Lindlar Catalyst
C
$Br _2$, aq $\cdot KOH , NaNH _2, H _2$ Lindlar Catalyst
D
$Br _2, aq \cdot KOH , NaNH _2, Na \left( Liq NH _3\right)$
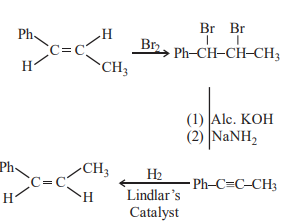
A
$OH ^{-}$is formed at cathode
B
$Cl _2$ is formed at cathode
C
$O _2$ is formed at cathode
D
$H _2$ is formed at anode
Solution
Electrolysis of brine solution
$NaCl ( aq .) \longrightarrow Na _{( aq )}^{+}+ Cl _{\text {(aq) }}^{+}$
At anode $: 2 Cl _{\text {(aq.) }}^{+} \longrightarrow \underset{\text { (Major) }}{ Cl _2( g )+2 e ^{-}}$
$2 H _2 O _{(\ell)} \longrightarrow \underset{\text { Minor }}{ O _{2( g )}}+4 H _{( aq )}^{+}+4 e ^{-}$
At Cathode : $2 H _2 O _{(\ell)}+2 e ^{-} \longrightarrow H _{2( g )} \uparrow+2 OH _{( aq )}^{-}$
$2 Na ^{+}+2 OH ^{-} \longrightarrow 2 NaOH$
A
$4 f ^3$
B
$4 f^4 6 s^2$
C
$4 f ^2 6 s ^2$
D
$4 f ^4$
Solution
$ Nd (60)=[ Xe ] 4 f ^4 5 d ^0 6 s ^2 $
$ Nd ^{2+}=[ Xe ] 4 f ^4 5 d ^0 5 s ^0$
A
$X = CuI _2 \,\,\,Y = Na _2 S _2 O _3$
B
$X = CuI _2 \,\,\, Y = Na _2 S _4 O _6$
C
$X = Cu _2 I _2 \,\,\,Y = Na _2 S _4 O _6$
D
$X = Cu _2 I _2 \,\,\, Y = Na _2 S _4 O _5$
Solution
$Cu ^{2+}+2 KI \longrightarrow \underset{\text { Unstable }}{ CuI _2} \downarrow+2 K ^{+}$
$I ^{-}$is strong R.A it reduces $Cu ^{2+}$ to $Cu ^{+}$
$2 CuI _2 \longrightarrow \underset{\text { (White)'X' }}{ Cu _2 I _2 \downarrow}+ I _2$
$KI + I _2 \longrightarrow K ^{+} I _3^{-} \text {(Brown solution) }$
$I _3^{-} \rightleftharpoons I _2+ I ^{-}$
$KI _3+ Na _2 S _2 O _3 \rightarrow KI + \underset{(Y)}{Na _2 S _4 O _6}$
A
$X = ClNO _3, Y = Cl _2, Z = NO _2$
B
$X = ClONO _2, Y = HOCl , Z = HNO _3$
C
$X = ClONO _2, Y = HOCl , Z = NO _2$
D
$X = ClNO _2, Y = HCl , Z = HNO _3$
Solution
$Cl \dot{ O }+ NO _2 \longrightarrow \underset{(x)}{ClO NO _2} \xrightarrow{ + H _2 O } \underset{( Y )}{ HOCl }+\underset{\text { (Z) }}{ HNO _3}$
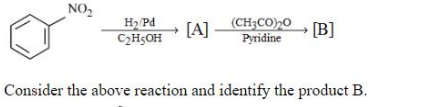
A
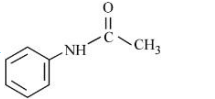
B
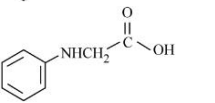
C
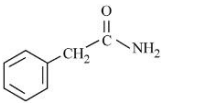
D
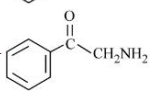
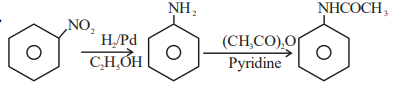
A
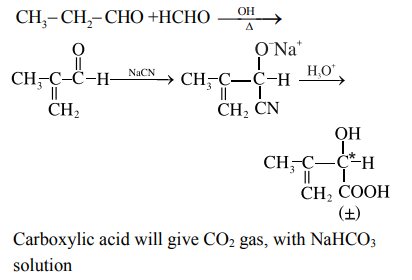
optically active and adds one mole of bromine
B
optically active alcohol and is neutral
C
racemic mixture and gives a gas with saturated $NaHCO _3$ solution
D
racemic mixture and is neutral
A
$Na _2 S +4 H _2 O _2 \rightarrow Na _2 SO _4+4 H _2 O$
B
$Mn ^{2+}+2 H _2 O _2 \rightarrow MnO _2+2 H _2 O$
C
$2 Fe ^{2+}+2 H ^{+}+ H _2 O _2 \rightarrow 2 Fe ^{3+}+2 H _2 O$
D
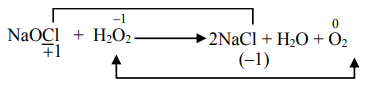
$2 NaOCl + H _2 O _2 \rightarrow 2 NaCl + H _2 O + O _2$
A
d
B
c
C
b
D
a
Solution
Non-Polar tail towards non-polar solvent
A
B, D and E only
B
$C , D$ and $E$ only
C
$A$ and $C$ only
D
B, D and C only
Solution
Methods involved in concentration of one are
(i) Hydraulic Washing
(ii) Froth Flotation
(iii) Magnetic Separation
(iv) Leaching
A
Alitane
B
Saccharin
C
Aspartame
D
Sucralose
Solution
Sweetness value order wrt cane sugar
Alitame > Sucralose > Saccharin > Aspartame
A
A-IV, B-I, C-II, D-III
B
A-II, B-I, C-III, D-IV
C
A-II, B-I, C-IV, D-III
D
A-IV, B-III, C-II, D-I
A
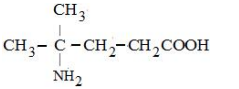
B
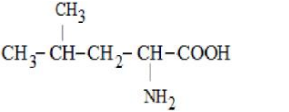
C
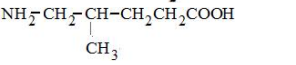
D
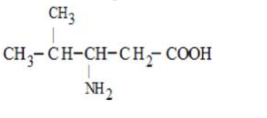
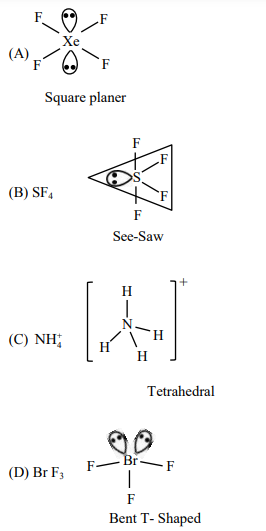
Solution
Only in option (2) $\alpha$-Amino acid is given all the other options are not $\alpha$-Amino acids.
A
A-(iii), B-(iv), C-(ii), D-(i)
B
A-(i), B-(iii), C-(ii), D-(iv)
C
A-(ii), B-(iv), C-(i), D-(iii)
D
A-(ii), B-(iii), C-(iv), D-(i)
Solution
A. $H _2 O / CH _2 Cl _2 \rightarrow$ ii, $CH _2 Cl _2> H _2 O$ (density) so they can be separated by differential solvent extraction.

C. Kerosene / Naphthalene $\rightarrow$ iv. Fractional distillation.
Due to different B.P. of kerosene and Naphthalene it can be separated by fractional distillation.
D. $C _6 H _{12} O _6 / NaCl \rightarrow$ i. Crystallization.
$NaCl$ (ionic compound) can be crystallized.
A
$X =\left[ Co \left( H _2 O \right)_4 Cl _2\right]^{+}, Y =\left[ CoCl _4\right]^{2-}, Z =$ Tetrahedral
B
$X =\left[ Co \left( H _2 O \right)_6\right]^{2+}, Y =\left[ CoCl _6\right]^{3-}, Z =$ Octahedral
C
$X =\left[ Co \left( H _2 O \right)_6\right]^{2+}, Y =\left[ CoCl _4\right]^{2-}, Z =$ Tetrahedral
D
$X =\left[ Co \left( H _2 O \right)_6\right]^{3+}, Y =\left[ CoCl _6\right]^{3-}, Z =$ Octahedral
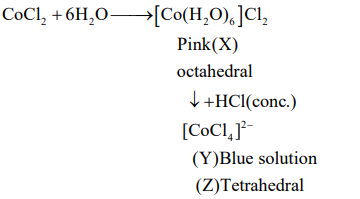
A
$Ca ^{2+}< K ^{+}< Cl ^{-}< S ^{2-}$
B
$S ^{2-}< Cl ^{-}< Ca ^{2+}< K ^{+}$
C
$K ^{+}< S ^{2-}< Ca ^{2+}< Cl ^{-}$
D
$Cl ^{-}< Ca ^{2+}< K ^{+}< S ^{2-}$
Solution
In isoelectronic species size $\propto \frac{1}{Z}$
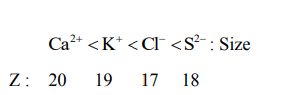
A
$V _2 O _3> V _2 O _5> V _2 O _4$
B
$V _2 O _4> V _2 O _3> V _2 O _5$
C
$V _2 O _3> V _2 O _4> V _2 O _5$
D
$V _2 O _5> V _2 O _4> V _2 O _3$
Solution
With increase in $\%$ of oxygen acidic nature of oxide of an element increase and basic nature decreases
Answer: 1
Solution
$SO _{2( g )}+\frac{1}{2} O _{2( g )} \rightleftharpoons SO _{3( g )} $
$ K _{ p }=2 \times 10^{12} \text { at } 300 K $
$ K _{ p }= K _{ C } \times( RT )^{\Delta n _{ g }} $
$ 2 \times 10^{12}= K _{ c } \times(0.082 \times 300)^{-1 / 2} $
$ K _{ C }=9.92 \times 10^{12} $
$ K _{ C }=0.992 \times 10^{13}$
$= 1$
Answer: 2520
Solution
$\log \frac{ K _{300}}{ K _{200}}=\frac{ E _{ a }}{2.3 \times 8.314}\left(\frac{1}{ T _1}-\frac{1}{ T _2}\right) $
$ \log \frac{0.05}{0.03}=\frac{ Ea }{2.305 \times 8.314} \times\left[\frac{1}{200}-\frac{1}{300}\right] $
$E _{ a }=2519.88 J \Rightarrow E _{ a }=2520 J $
Answer: 555
Solution
$P _{ x }=\chi_{ X } P _{ T } $
$ =\frac{\frac{0.6}{20}}{\frac{0.6}{20}+\frac{0.45}{45}} \times 740 $
$ P _{ X }=555 \,mm \,Hg$
Answer: 62250
Solution
$= CRT $
$ \frac{400 Pa }{10^5}=\frac{\frac{2.5 g }{ M _{ o }}}{250 / 1000 L } \times 0.83 \frac{ L - bar }{ K \cdot mol } \times 300\, K $
$M _{ o }=62250$
Answer: 44
Solution
weight of $C$ in $0.792\, gm\, CO _2$
$=\frac{12}{44} \times 0.792=0.216$
$ \% $ of $ C$ in compound $=\frac{0.216}{0.492} \times 100 $
$ =43.90 \%$
$=44$
Answer: 4
Solution
$ Zn +2 HCl \rightarrow ZnCl _2+ H _2 \uparrow$
$\text { Moles of } Zn \text { used }=\frac{11.5}{65.4}=\text { Moles of } H _2 \text { evolved } $
$ \text { Volume of } H _2=\frac{11.5}{65.4} \times 22.7 L =3.99 L$
$=4$
Answer: 6
Solution
$ \Delta G ^0=- RT \ell nK $
$ - nFE _{\text {cell }}^o=- RT \times 2.303\left(\log _{10} K \right) $
$ \frac{ E _{\text {Cell }}^0}{0.06} \times n =\log K $....(1)
$ Pd ^{+2} \text { (aq.) }+\not \not e ^{-} \rightleftharpoons Pd ( s ), E _{\text {cat,red }}^n=0.83$
$Pd ( s )+4 Cl ^{-}( aq .) \rightleftharpoons PdCl _4^{2-},( aq )+2 e ^{-}, E _{\text {Anode, oxiad }}^n=0.65$
Net Reaction $\rightarrow Pd ^{2+}$ (aq.) $+4 Cl ^{-}$(aq.) $\rightleftharpoons PdCl _4^{2-}$ (aq.)
$ E _{\text {cell }}^{ o }= E _{\text {cat,red}^n }^{ \circ }- E _{\text {Anode,oxid}^n }^{ \circ } $
$ E _{\text {cell }}^{ o }=0.83-0.65$
$ E _{\text {cell }}^{ o }=0.18$...(2)
Also $n =2$.....(3)
Using equation (1), (2) & (3) $\log K =6$
Answer: 610
Solution
$ \frac{1}{2} Cl _{2( g )} \rightarrow Cl _{( g )} \rightarrow Cl _{( g )}^{-} \rightarrow Cl _{( aq .)}^{-}$
$\Delta H ^{\circ}=\frac{1}{2} \times 240+(-350)+(-380) $
$ =-610 $
JEE Main Mathematics Question Paper with Solution 2023 January 31st Shift 1 - Morning
A
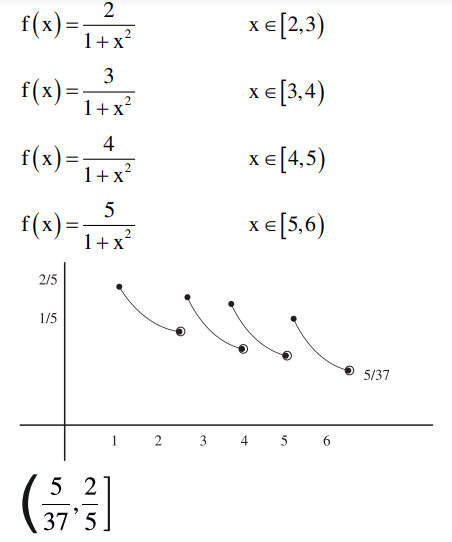
$\left(\frac{5}{37}, \frac{2}{5}\right]$
B
$\left(\frac{5}{26}, \frac{2}{5}\right]-\left\{\frac{9}{29}, \frac{27}{109}, \frac{18}{89}, \frac{9}{53}\right\}$
C
$\left(\frac{5}{26}, \frac{2}{5}\right]$
D
$\left(\frac{5}{37}, \frac{2}{5}\right]-\left\{\frac{9}{29}, \frac{27}{109}, \frac{18}{89}, \frac{9}{53}\right\}$
A
$\frac{2}{7}$
B
$\frac{3}{7}$
C
$\frac{5}{7}$
D
$\frac{5}{6}$
Solution
$ \frac{{ }^5 C _2+{ }^6 C _2}{{ }^2 C _2+{ }^3 C _2+{ }^4 C _2+{ }^5 C _2+{ }^8 C _2}=\frac{10+15}{1+3+6+10+15} $
$ =\frac{25}{35}=\frac{5}{7}$
A
$\frac{9}{2}$
B
3
C
7
D
14
Solution
$ a, a r, a r^2, a r^3(a, r>0) $
$ a^4 r^6=1296 $
$ a^2 r^3=36 $
$ a=\frac{6}{r^{3 / 2}} $
$ a+a r+a r^2+a r^3=126 $
$ \frac{1}{r^{3 / 2}}+\frac{r}{r^{3 / 2}}+\frac{r^2}{r^{3 / 2}}+\frac{r^3}{r^{3 / 2}}=\frac{126}{6}=21 $
$ \left(r^{-3 / 2}+r^{3 / 2}\right)+\left(r^{1 / 2}+r^{-1 / 2}\right)=21 $
$ r^{1 / 2}+r^{-1 / 2}=A$
$ r^{-3 / 2}+r^{3 / 2}+3 A=A^3$
$ A ^3-3 A + A =21 $
$ A ^3-2 A =21 $
$ A =3 $
$ \sqrt{r}+\frac{1}{\sqrt{r}}=3 $
$ r +1=3 \sqrt{r} $
$ r ^2+2 r +1=9 r $
$ r ^2-7 r +1=0$
A
$2 y^{\prime}+\sqrt{3} \pi^2 y=0$
B
$\sqrt{2} y^{\prime}-3 \pi^2 y=0$
C
$2 y^{\prime}+3 \pi^2 y=0$
D
$y^{\prime}+3 \pi^2 y=0$
Solution
$ y =\sin ^3(\pi / 3 \operatorname{cosg}(x))$
$ g(x)=\frac{\pi}{3 \sqrt{2}}\left(-4 x^3+5 x^2+1\right)^{3 / 2} $
$ g(1)=2 \pi / 3 $
$ y^{\prime}=3 \sin ^2\left(\frac{\pi}{3} \cos g(x)\right) \times \cos \left(\frac{\pi}{3} \cos g(x)\right) $$\times \frac{\pi}{3}(-\sin g(x)) g^{\prime}(x)$
$ y^{\prime}(1)=3 \sin ^2\left(-\frac{\pi}{6}\right) \cdot \cos \left(\frac{\pi}{6}\right) \cdot \frac{\pi}{3}\left(-\sin \frac{2 \pi}{3}\right) g^{\prime}(1) $
$ g^{\prime}(x)=\frac{\pi}{3 \sqrt{2}}\left(-4 x^3+5 x^2+1\right)^{1 / 2}\left(-12 x^2+10 x\right)$
$ g^{\prime}(1)=\frac{\pi}{2 \sqrt{2}}(\sqrt{2})(-2)=-\pi $
$y^{\prime}(1)=\frac{\not 3}{4} \cdot \frac{\sqrt{3}}{2} \cdot \frac{\pi}{\not 3 }\left(\frac{-\sqrt{3}}{2}\right)(-\pi)=\frac{3 \pi^2}{16}$
$ y(1)=\sin ^3(\pi / 3 \cos 2 \pi / 3)=-\frac{1}{8} $
$ 2 y^{\prime}(1)+3 \pi^2 y(1)=0$
A
2
B
3
C
1
D
0
Solution
$ \sqrt{(x-1)(x-3)}+\sqrt{(x-3)(x+3)} $
$ =\sqrt{4\left(x-\frac{12}{4}\right)\left(x-\frac{2}{4}\right)} $
$ \Rightarrow \sqrt{x-3}=0 \Rightarrow x=3 \text { which is in domain }$
$ \text { or }$
$ \sqrt{x-1}+\sqrt{x+3}=\sqrt{4 x-2}$
$ 2 \sqrt{(x-1)(x+3)}=2 x-4$
$x^2+2 x-3=x^2-4 x+4 $
$ 6 x=7 $
$ x=7 / 6$(rejected)
A
both (S1) and (S2) are correct
B
only (S2) is correct
C
only ( S 1) is correct
D
both ( S 1) and (S2) are wrong
Solution
$p$
$q$
$p \Rightarrow q$
$\sim q$
$p \wedge \sim q$
$(p \Rightarrow q) \vee(p \wedge \sim q)$
T
T
T
F
F
T
T
F
F
T
T
T
F
T
T
F
F
T
F
F
T
T
F
T
$\sim p$
$\sim q$
$\sim p \Rightarrow \sim q$
$\sim p \vee q$
$((\sim p) \Rightarrow(\sim q)) \wedge(\sim p) \vee q)$
F
F
T
T T
F
T
T
F F
T
F
F
T F
T
T
T
T T
| $p$ | $q$ | $p \Rightarrow q$ | $\sim q$ | $p \wedge \sim q$ | $(p \Rightarrow q) \vee(p \wedge \sim q)$ |
|---|---|---|---|---|---|
| T | T | T | F | F | T |
| T | F | F | T | T | T |
| F | T | T | F | F | T |
| F | F | T | T | F | T |
| $\sim p$ | $\sim q$ | $\sim p \Rightarrow \sim q$ | $\sim p \vee q$ | $((\sim p) \Rightarrow(\sim q)) \wedge(\sim p) \vee q)$ |
|---|---|---|---|---|
| F | F | T | T | T |
| F | T | T | F | F |
| T | F | F | T | F |
| T | T | T | T | T |
A
$\alpha+2 y=24$
B
$2 \alpha+\gamma=7$
C
$\alpha-2 \gamma=19$
D
$2 \alpha-\gamma=9$
Solution
$\vec{ b _1} \times \vec{ b _2}=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ -2 & 0 & 1 \\ 1 & 1 & -1\end{vmatrix}=-\hat{ i }-\hat{ j }-2 \hat{ k }$
$ \vec{ a _2}-\vec{ a _1}=6 \hat{ i }+(\lambda-1) \hat{ j }+(-\lambda-4) \hat{ k } $
$ 2 \sqrt{6}=\left|\frac{-6-\lambda+1+2 \lambda+8}{\sqrt{1+1+4}}\right|$
$|\lambda+3|=12 \Rightarrow \lambda=9,-15 $
$ \alpha=-2 k +5, \gamma= k -\lambda \text { where } k \in R $
$ \Rightarrow \alpha+2 \gamma=5-2 \lambda=-13,35$
A
both (A) and (B) are correct
B
only $( A )$ is correct
C
only (B) is correct
D
neither $( A )$ nor $(B)$ is correct
Solution
$ |\vec{a}+\vec{b}+\vec{c}|^2=|\vec{a}+\vec{b}-\vec{c}|^2$
$ 2 \vec{a} \cdot \vec{b}+2 \vec{b} \cdot \vec{c}+2 \vec{c} \cdot \vec{a}=2 \vec{a} \cdot \vec{b}-2 \vec{b} \cdot \vec{c}-2 \vec{c} \cdot \vec{a}$
$4 \vec{a} \cdot \vec{c}=0$
$B$ is incorrect
$ |\vec{ a }+\lambda \vec{ c }|^2 \geq|\vec{ a }|^2 $
$ \lambda^2 c ^2 \geq 0$
True $\forall \lambda \in R$ (A) is correct.
A
$P_{50}(\alpha)-\beta$
B
$-\left(\beta+P_{50}(\alpha)\right)$
C
$\beta+P_{50}(a)$
D
$\beta-P_{50}(\alpha)$
Solution
$ \int\limits_0^\alpha \frac{t^{50}-1+1}{1-t}=-\int\limits_0^\alpha\left(1+ t +\ldots . .+ t ^{49}\right)+\int\limits_0^\alpha \frac{1}{1- t } dt $
$ =-\left(\frac{\alpha^{50}}{50}+\frac{\alpha^{49}}{49}+\ldots . .+\frac{\alpha^1}{1}\right)+\left(\frac{\ln (1- f )}{-1}\right)_0^\alpha$
$ =- P _{50}(\alpha)-\ln (1-\alpha)$
$ =- P _{50}(\alpha)-\beta$
A
2050
B
4094
C
6144
D
4097
Solution
$A^2=\begin{bmatrix}1 & 0 & 0 \\ 0 & 4 & -1 \\ 0 & 12 & -3\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\ 0 & 4 & -1 \\ 0 & 12 & -3\end{bmatrix}$
$=\begin{bmatrix}1 & 0 & 0 \\ 0 & 4 & -1 \\ 0 & 12 & -3\end{bmatrix}= A$
$ \Rightarrow A ^3= A ^4=\ldots \ldots= A $
$ ( A + I ){ }^{11}={ }^{11} C _0 A ^{11}+{ }^{11} C _1 A ^{10}+\ldots . \cdot{ }^{11} C _{10} A +{ }^{11} C _{11} I $
$ =\left({ }^{11} C _0+{ }^{11} C _1+\ldots .{ }^{11} C _{10}\right) A + I$
$ =\left(2^{11}-1\right) A + I =2047 A + I $
$ \therefore $ Sum of diagonal elements $=2047(1+4-3)+3 $
$ =4094+3=4097$
A
the curve $C_1$ lies inside $C_2$
B
the curves $C_1$ and $C_2$ intersect at 4 points
C
the curve $C_2$ lies inside $C_1$
D
the curves $C_1$ and $C_2$ intersect at 2 points
Solution
Let $w = z +\frac{1}{ z }=4 e ^{ i \theta}+\frac{1}{4} e ^{-i \theta}$
$\Rightarrow w =\frac{17}{4} \cos \theta+ i \frac{15}{4} \sin \theta$
So locus of w is ellipse $\frac{x^2}{\left(\frac{17}{4}\right)^2}+\frac{y^2}{\left(\frac{15}{4}\right)^2}=1$
Locus of $z$ is circle $x ^2+ y ^2=16$
So intersect at 4 points
A
$16-5 \pi$
B
16
C
0
D
$\pi$
Solution
$ \cos ^{-1} \frac{4}{5}=\tan ^{-1} \frac{3}{4} $
$ \therefore \sin ^{-1} \frac{\alpha}{17}=\tan ^{-1} \frac{77}{36}-\tan ^{-1} \frac{3}{4}=\tan ^{-1}\left(\frac{\frac{77}{36}-\frac{3}{4}}{1+\frac{77}{36} \cdot \frac{3}{4}}\right) $
$ \sin ^{-1} \frac{\alpha}{17}=\tan ^{-1} \frac{8}{15}=\sin ^{-1} \frac{8}{17}$
$ \Rightarrow \frac{\alpha}{17}=\frac{8}{17} \Rightarrow \alpha=8$
$\therefore \sin ^{-1}(\sin 8)+\cos ^{-1}(\cos 8)$
$ =3 \pi-8+8-2 \pi $
$ =\pi$
A
If $\alpha=\beta$ and $\alpha \neq 7$, then the system has a unique solution
B
There is a unique point $(\alpha, \beta)$ on the line $x+2 y+18=0$ for which the system has infinitely many solutions
C
For every point $(\alpha, \beta) \neq(7,7)$ on the line $x-2 y+7=0$, the system has infinitely many solutions
D
If $\alpha=\beta=7$, then the system has no solution
Solution
By equation 1 and 3
$y+2 z=8 $
$y=8-2 z $
And $x=-2+z$
Now putting in equation 2
$\alpha(z-2)+\beta(-2 z+8)+7 z=3 $
$ \Rightarrow(\alpha-2 \beta+7) z=2 \alpha-8 \beta+3$
So equations have unique solution if $\alpha-2 \beta+7 \neq 0$
And equations have no solution if $\alpha-2 \beta+7=0$ and $2 \alpha-8 \beta+3 \neq 0$
And equations have infinite solution if $\alpha-2 \beta+7=0$ and $2 \alpha-8 \beta+3=0$
A
transitive but neither reflexive nor symmetric
B
symmetric but neither reflexive nor transitive
C
symmetric and transitive but not reflexive
D
reflexive and symmetric but not transitive
Solution
$\text { (a, b) } R(c, d) \Rightarrow a d(b-c)=b c(a-d)$
Symmetric:
$(c, d) R(a, b) \Rightarrow c b(d-a)=d a(c-b) \Rightarrow$
Symmetric Reflexive:
(a, b) $R(a, b) \Rightarrow a b(b-a) \neq b a(a-b) \Rightarrow$
Not reflexive
Transitive: $(2,3) R (3,2)$ and $(3,2) R (5,30)$ but
$((2,3),(5,30)) \notin R \Rightarrow \text { Not transitive }$
A
$\frac{7}{2}-\sqrt{3}-\log _e \sqrt{3}$
B
$\frac{10}{3}-\sqrt{3}-\log _e \sqrt{3}$
C
$\frac{10}{3}-\sqrt{3}+\log _e \sqrt{3}$
D
$-2+3 \sqrt{3}+\log _e \sqrt{3}$
Solution
$ \int\limits_{\pi / 3}^{\pi / 2}\left(\frac{2+3 \sin x}{\sin x(1+\cos x)}\right) d x=2 \int\limits_{\pi / 3}^{\pi / 2} \frac{d x}{\sin x+\sin x \cos x}+3$
$ 3 \int\limits_{\pi / 3}^{\pi / 2} \frac{d x}{1+\cos x} $
$\int\limits_{\pi / 3}^{\pi / 2} \frac{d x}{1+\cos x}=\int\limits_{\pi / 3}^{\pi / 2} \frac{1-\cos x}{\sin ^2 x} d x $
$ =\int\limits_{\pi / 3}^{\pi / 2}\left(\text{cosec}^2 x-\cot x \text{cosec} x\right) d x$
$ =(\operatorname{cosec} x-\cot x) \int\limits_{\pi / 3}^{\pi / 2}=(1)-\left(\frac{2}{\sqrt{3}}-\frac{1}{\sqrt{3}}\right)=1-\frac{1}{\sqrt{3}} $
$ \int\limits_{\pi / 3}^{\pi / 2} \frac{d x}{\sin x(1+\cos x)}= $
$ \int \frac{d x}{(2 \tan x / 2)\left(1+1-\tan ^2 x / 2\right)}$
$ =\int \frac{\left(1+\tan ^2 x / 2\right) \sec ^2 x / 2 d x}{2 \tan x / 2}$
$ \tan x / 2= t $
$ \sec x / 2 \frac{1}{2} dx = dt$
$ \frac{1}{2} \int\left(\frac{1+ t ^2}{ t }\right) dt =\frac{1}{2}\left[\ln +\frac{ t }{2}^2\right]_{\frac{1}{\sqrt{3}}}^1 $
$ =\frac{1}{2}\left[\left(0+\frac{1}{2}\right)-\left(\ln \frac{1}{\sqrt{3}}+\frac{1}{6}\right)\right]=\left(\frac{1}{3}+\ln \sqrt{3}\right) \frac{1}{2} $
$ =\left(\frac{1}{6}+\frac{1}{2} \ln \sqrt{3}\right) $
$ 2\left(\frac{1}{6}+\frac{1}{2} \ln \sqrt{3}\right)+3\left(1-\frac{1}{\sqrt{3}}\right) $
$ =\frac{1}{3}+\ln \sqrt{3}+3-\sqrt{3}=\frac{10}{3}+\ln \sqrt{3}-\sqrt{3}$
A
$6: 1$
B
$3: 1$
C
$4: 1$
D
$1: 6$
Solution
$ \ell_1+\ell_2=20 \Rightarrow \frac{ d \ell_2}{ d \ell_1}=-1$
$ A _1=\left(\frac{\ell_1}{4}\right)^2 \text { and } A _2=\pi\left(\frac{\ell_2}{2 \pi}\right)^2$
Let $S =2 A _1+3 A _2=\frac{\ell_1^2}{8}+\frac{3 \ell_2^2}{4 \pi}$
$ \frac{ ds }{ d \ell}=0 \Rightarrow \frac{2 \ell_1}{8}+\frac{6 \ell_2}{4 \pi} \cdot \frac{ d \ell_2}{ d \ell_1}=0$
$\Rightarrow \frac{\ell_1}{4}=\frac{6 \ell_2}{4 \pi} \Rightarrow \frac{\pi \ell_1}{\ell_2}=6$
A
$\frac{\sqrt{3}}{4}$
B
$\frac{\sqrt{3}}{2}$
C
$\frac{1}{\sqrt{2}}$
D
$\frac{1}{2}$
Solution
Equation of normal is
$2 x \sec \theta-\text { by } \operatorname{cosec} \theta=4-b^2$
Distance from $(0,0)=\frac{4-b^2}{\sqrt{4 \sec ^2 \theta+b^2 \operatorname{cosec}^2 \theta}}$
Distance is maximum if
$4 \sec ^2 \theta+b^2 \operatorname{cosec}^2 \theta$ is minimum
$ \Rightarrow \tan ^2 \theta=\frac{b}{2} $
$\Rightarrow \frac{4-b^2}{\sqrt{4 \cdot \frac{b+2}{2}+b^2 \cdot \frac{b+2}{b}}}=1 $
$ \Rightarrow 4-b^2=b+2 \Rightarrow b=1 \Rightarrow e =\frac{\sqrt{3}}{2}
$
A
19
B
17
C
1
D
34
Solution
Differentiate w.r.t. x
$ f^{\prime}(x)+\frac{f(x)}{x}=\frac{1}{2 \sqrt{x+1}} $
$ \text { I.F. }=e^{\int \frac{1}{x} d x}=e^{\ln x}=x $
$ x f(x)=\int \frac{x}{2 \sqrt{x+1}} d x$
$ x+1=t^2$
$ =\int \frac{t^2-1}{2 t} 2 t d t $
$ x f(x)=\frac{t^3}{3}-t+c$
$ x f(x)=\frac{(x+1)^{3 / 2}}{3}-\sqrt{x+1}+c$
Also putting $x=3$ in given equation $f(3)+0=\sqrt{4}$
$ f (3)=2 $
$ \Rightarrow C =8-\frac{8}{3}=\frac{16}{3} $
$ f ( x )=\frac{\frac{( x +1)^{3 / 2}}{3}-\sqrt{ x +1}+\frac{16}{3}}{ x } $
$ f (8)=\frac{9-3+\frac{16}{3}}{8}=\frac{34}{24}$
$ \Rightarrow 12 f (8)=17$
A
is an empty set
B
contains exactly one element
C
contains exactly two elements
D
is an infinite set
Solution
$ \left(x+\frac{1}{2}\right)^2=\left(y+\frac{1}{4}\right)$
$ y=\left(x^2+x\right) $
$ \tan ^{-1} \sqrt{x(x+1)}+\sin ^{-1} \sqrt{x^2+x+1}=\pi / 2$
$ 0 \leq x^2+x+1 \leq 1$
$x^2+x \leq 0 $....(1)
$ \text { Also } x^2+x \geq 0 $....(2)
$ \therefore x^2+x=0 \Rightarrow x=0,-1$
$S$ contains 2 element.
A
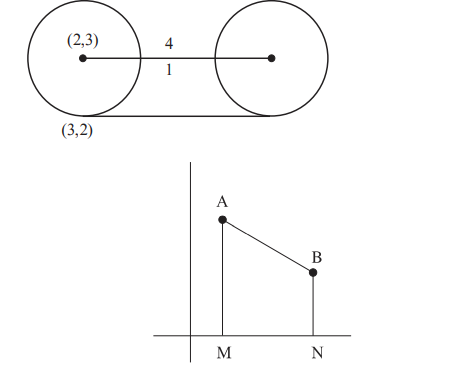
$2(2+\sqrt{2})$
B
$2(1+\sqrt{2})$
C
$4(1+\sqrt{2})$
D
$3+2 \sqrt{2}$
Solution
$C =(2,3), r =\sqrt{2} $
Centre of $G = A =2+4 \frac{1}{\sqrt{2}}, $
$ 3+\frac{4}{\sqrt{2}}=(2+2 \sqrt{2}, 3+2 \sqrt{2})$
$ A (2+2 \sqrt{2}, 3+2 \sqrt{2})$
$B (4+2 \sqrt{2}, 1+2 \sqrt{2})$
$ \frac{ x -(2+2 \sqrt{2})}{1}=\frac{ y -(3+2 \sqrt{2})}{-1}=2 $
$\therefore \text { area of trapezium: } $
$\frac{1}{2}(4+4 \sqrt{2}) 2=4(1+\sqrt{2})$
Answer: 2
Solution
$ T _{ r +1}={ }^{30} C _{ r }\left( x ^{2 / 3}\right)^{30- r }\left(\frac{2}{ x ^3}\right)^{ r } $
$ ={ }^{30} C _{ r } \cdot 2^{ r } \cdot x ^{\frac{60-11 r }{3}} $
$ \frac{60-11 r }{3}<0 \Rightarrow 11 r >60 \Rightarrow r >\frac{60}{11} \Rightarrow r =6$
$ T _7={ }^{30} C _6 \cdot 2^6 x ^{-2}$
We have also observed $\beta={ }^{30} C _6(2)^6$ is a natural number.
$\therefore \alpha=2$
Answer: 9
Solution

$ \cos \theta=\frac{(\hat{ i }+\hat{ j }+2 \hat{ k }) \cdot(2 \hat{ i }-\hat{ j }+\hat{ k })}{6}=\frac{2-1+2}{6}=\frac{1}{2} $
$ \theta=\pi / 3 $
$\alpha=\pi / 6$
$ \left(\tan ^2 \theta\right)\left(\cot ^2 \alpha\right)$
$(3) (3)=9$
Answer: 9
Solution
$ 5^{9 9}=5^4 .5^{95} $
$ =625\left[5^5\right]^{19} $
$ =625[3125]^{19} $
$ =625[3124+1]^{19} $
$ =625[11 k \times 19+1] $
$ =625 \times 11 k \times 19+625$
$ =11 k _1+616+9$
$ =11\left( k _2\right)+9 $
Remainder $=9$
Answer: 8
Solution
$2 a_5=a_5(\text { given }) $
$ 2\left(a_1+6 d\right)=a_1+4 d $
$ a_1+8 d=0 $....(1)
$ a_1+10 d=18 $...(2)
$ \text { By }(1) \text { and (2) we get } a_1=-72, d=9 $
$ a_{18}=a_1+17 d=-72+153=81 $
$ a_{10}=a_1+9 d=9 $
$ 12\left(\frac{\sqrt{a_{11}}-\sqrt{a_{10}}}{d}+\frac{\sqrt{a_{12}}-\sqrt{a_{11}}}{d}+\ldots \ldots \frac{\sqrt{a_{18}}-\sqrt{a_{17}}}{d}\right) $
$ 12\left(\frac{\sqrt{a_{18}}-\sqrt{a_{10}}}{d}\right)=\frac{12(9-3)}{9}=\frac{12 \times 6}{6}=8$
Answer: 5
Solution
$x_i$
$f_i$
$d_i =
x_i
- 5$
$f_i
d_i
^2$
$f_id_i$
2
3
-3
27
-9
3
6
-2
24
-12
4
16
-1
16
-16
5
$\alpha$
0
0
0
6
9
1
9
9
7
5
2
20
10
8
6
3
54
18
$ \sigma_x^2=\sigma_d^2=\frac{\sum f _{ i } d _{ i }{ }^2}{\sum f _{ i }}-\left(\frac{\sum f _{ i } d _{ i }}{\sum f _{ i }}\right)^2 $
$ =\frac{150}{45+\alpha}-0=3 $
$\Rightarrow 150=135+3 \alpha$
$ \Rightarrow 3 \alpha=15 \Rightarrow \alpha=5$
| $x_i$ | $f_i$ | $d_i = x_i - 5$ | $f_i d_i ^2$ | $f_id_i$ |
|---|---|---|---|---|
| 2 | 3 | -3 | 27 | -9 |
| 3 | 6 | -2 | 24 | -12 |
| 4 | 16 | -1 | 16 | -16 |
| 5 | $\alpha$ | 0 | 0 | 0 |
| 6 | 9 | 1 | 9 | 9 |
| 7 | 5 | 2 | 20 | 10 |
| 8 | 6 | 3 | 54 | 18 |
Answer: 36
Solution
$ |\vec{a}|=\sqrt{14},|\vec{b}|=\sqrt{6} \quad|\vec{a} \times \vec{b}|=\sqrt{48} $
$ |\vec{a} \times \vec{b}|^2+|\vec{a} \cdot \vec{b}|^2=|\vec{a}|^2 \times|\vec{b}|^2$
$ \Rightarrow(\vec{a} \cdot \vec{b})^2=84-48=36$
Answer: 180
Solution
Any point on $L ((2 \lambda+1),(-\lambda-1),(\lambda+3))$
$ 2(2 \lambda+1)+(-\lambda-1)+3(\lambda+3)=16$
$6 \lambda+10=16 \Rightarrow \lambda=1 $
$ \therefore P =(3,-2,4)$
$DR$ of $QR =\langle 2 \lambda,-\lambda, \lambda+6\rangle$
$DR$ of $L =\langle 2,-1,1\rangle$
$4 \lambda+\lambda+\lambda+6=0 $
$ 6 \lambda+6=0 \Rightarrow \lambda=-1 $
$Q=(-1,0,2)$

$\overrightarrow{ QR } \times \overrightarrow{ QP }=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 2 & -1 & -5 \\ 4 & -2 & 2\end{vmatrix}=-12 \hat{ i }-24 \hat{ j }$
$\alpha=\frac{1}{2} \times \sqrt{144+576} \Rightarrow \alpha^2=\frac{720}{4}=180$
Answer: 710
Solution
$1000-2799$
Divisible by 3
$1002+(n-1) 3=2799$
$n=600$
Divisible by 11
$ 1-2799 \rightarrow\left[\frac{2799}{11}\right]=[254]=254$
$ 1-999=\left[\frac{999}{11}\right]=90 $
$ 1000-2799=254-90=164$
Divisible by 33
$ 1-2799 \rightarrow\left[\frac{2799}{33}\right]=84 $
$ 1-999 \rightarrow\left[\frac{999}{33}\right]=30$
$ 1000-2799 \rightarrow 54$
$ \therefore n (3)+ n (11)- n (33) $
$ 600+164-54=710$
Answer: 72
Solution

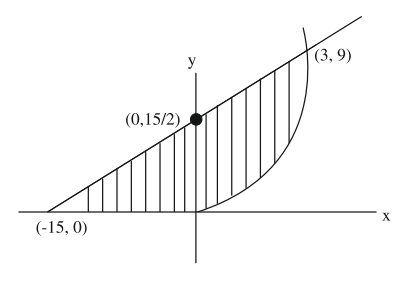
$ 2 y - x =15 $
$ A =\int\limits_0^3\left(\frac{ x +15}{2}- x ^2\right) dx +\frac{1}{2} \times \frac{15}{2} \times 15 $
$ \frac{ x ^2}{4}+\frac{15 x }{2}-\left.\frac{ x ^3}{3}\right|_0 ^3+\frac{225}{4} $
$ =\frac{9}{4}+\frac{45}{2}-9+\frac{225}{4}=\frac{99-36+225}{4}$
$ =\frac{288}{4}=72$