JEE Advanced Physics Question Paper with Solution JE Advanced 2022 Paper 2
Answer: 3
Solution
Torque about origin is zero
So angular momentum about origin remains conserved.
$\begin{array}{l}
\left|\begin{array}{ccc}
i & j & k \\
\frac{1}{\sqrt{2}} & \sqrt{2} & 0 \\
-\sqrt{2} & \sqrt{2} & \frac{2}{\pi}
\end{array}\right|=\left|\begin{array}{ccc}
i & j & k \\
x & y & 0.5 \\
v _x & v _y & \frac{2}{\pi}
\end{array}\right| \\
\hat{ i }\left[\sqrt{2} \times \frac{2}{\pi}\right]-\hat{ j }\left[\frac{\sqrt{2}}{\pi}\right]+\hat{ k }[1+2]= i \left[\frac{ y \times 2}{\pi}-0.5 v _y\right]-\hat{ j }\left[\frac{ x \times 2}{\pi}-0.5 v _x\right]+ k \left[ xv _y- yv v _x\right] \\
x v_y-y v_x=3 \\
\end{array}
$
Answer: 2
Solution
$ Th _{90}^{230} \rightarrow Po _{84}^{214}+ n _2^4+ m \beta_{-1}^0 $
$ 230=214+4 n $
$ n =\frac{16}{4}=4 $
$90=84+ n \times 2- m \times 1$
$90=84+4 \times 2- m \times 1$
$ m =92-90=2$
Hence $\frac{ n }{ m }=\frac{4}{2}=2$ Ans.
Answer: 5
Solution
For the balanced Wheatstone bridge
$\frac{ R _1}{ R _2}=\frac{\int\limits_0^{0.5} \frac{\rho dx }{\pi r _x^2}}{\int\limits_{0.5}^1 \frac{\rho dx }{\pi r _{ x }^{2}}} $
$ \frac{ R _1}{ R _2}=\frac{+\left[\frac{1}{ r _{ x }}\right]_0^{0.5}}{+\left[\frac{1}{ r _{ x }}\right]_{0.5}^1} $
$ \therefore R _1=5 R _2=5 \Omega$
Answer: 4
Solution
$ B = e ^\alpha\left( m _{ e }\right)^\beta h ^\gamma k ^\delta$
${[ B ]=\left[ e ^\alpha\right]\left[ m _{ e }\right]^\beta[ h ]^\gamma\left[ k ^\delta\right]} $
$ {\left[ M ^1 T ^{-2} A ^{-1}\right]=[ AT ]^\alpha\left[ m ^\beta\right]^{[}\left[ ML ^2 T ^{-1}\right]^\gamma\left[ ML ^3 A ^{-2} T ^{-4}\right]^\delta} $
$M ^1 T ^{-2} A ^{-1}= m ^{\beta+\gamma+\delta} L ^{2 r +3\delta} T ^{\alpha-\gamma-4\delta} A ^{\alpha-2 \delta}$
Compare : $\beta+\gamma+\delta=1 ; 2 \gamma+3 \delta=0, \alpha-\gamma-4 \delta=-2, \alpha-2 \delta=-1$
On solving $\alpha=3, \beta=2, \gamma=-3, \delta=2$
$\alpha+\beta+\gamma+\delta=4$
Answer: 4
Solution

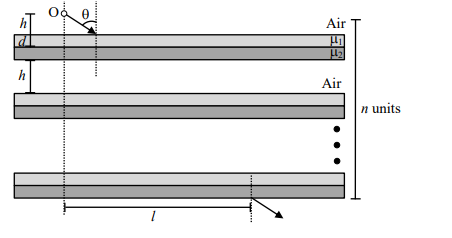
$1 \sin 60^{\circ}=\sqrt{\frac{3}{2}} \sin \theta$
$ \Rightarrow \theta_1=45^{\circ}$
$ \sqrt{\frac{3}{2}} \sin 45^{\circ}=\sqrt{3} \sin \theta_2$
$ =\sqrt{\frac{3}{2}} \frac{1}{\sqrt{2}}=\sqrt{3} \sin \theta_2 $
$ =\theta_2=30^{\circ}$
$h \tan 60^{\circ}+d \tan 45^{\circ}+d \tan 30^{\circ}$
$ \frac{1}{3} \sqrt{3}+\left(\frac{\sqrt{3}-1}{2}\right)+\left(\frac{\sqrt{3}-1}{2}\right) \frac{1}{\sqrt{3}} $
$ \frac{2 \sqrt{3}+3 \sqrt{3}-3+3-\sqrt{3}}{6}$
$ \frac{4 \sqrt{3}}{6} $
$\therefore n \frac{4 \sqrt{3}}{6}=\frac{8}{\sqrt{3}}$
$n = 4$
Answer: 3
Solution
From Gauss law,
$\phi_{\text {hemisphere }}+\phi_{\text {Cone }}=\frac{ q }{\varepsilon_0} \ldots . .$ (i)
Total flux produced from $q$ in $\alpha$ angle
$\phi=\frac{ q }{2 \varepsilon_0}[1-\cos \alpha]$
For hemisphere, $\alpha=\frac{\pi}{2}$
$\phi_{\text {hemisphere }}=\frac{ q }{2 \varepsilon_0}$
From equation (i)
$=\frac{ q }{2 \varepsilon_0}+\phi_{\text {cone }}=\frac{ q }{\varepsilon_0} $
$ \phi_{\text {cone }}=\frac{ q }{2 \varepsilon_0} $
$ \frac{4 q }{6 \varepsilon_0}=\frac{ q }{2 \varepsilon_0}$
$n =3$
Alternatively, $\phi \propto$ no of electric field lines passing through surface $q$ is point charge which has uniformly distributed electric field lines thus half of electric field lines will pass through hemisphere & other half will pass through conical surface.
Answer: 6
Solution

$ \ell>\ell_0 \rightarrow k = k _1$
$ \ell<\ell_0 \rightarrow k = k _2$
Time period of oscillation,
$ T =\pi \sqrt{\frac{ m }{ k _1}}+\pi \sqrt{\frac{ m }{ k _2}} $
$ T =\pi \sqrt{\frac{0.1}{0.009}}+\pi \sqrt{\frac{0.1}{0.016}}$
$T =\frac{\pi}{0.3}+\frac{\pi}{0.4} \Rightarrow T =\frac{0.7}{0.12} \pi \Rightarrow T =5.83 \pi$
$ T \approx 6 \pi $
So, $ n =6$
Answer: 3
Solution

$u =-30 \,cm $
$ f =-10 \,cm$
$ v =\frac{ f _0}{ u - f }=-15 \, cm $
$ \frac{1}{ v }+\frac{1}{ u }=\frac{1}{ f } $
$\frac{ du }{ dt }=-\frac{ v ^2}{ u ^2} \frac{ du }{ dt } $
$ \overrightarrow{ v }_{ lm }=-\left(\frac{ v }{ u }\right)^2 \overrightarrow{ v }_{ om }$
Given $\vec{v}_1=\overrightarrow{0}$
$ \overrightarrow{ v }_1-\overrightarrow{ v }_{ m }=-\left(\frac{-15}{-30}\right)^2\left(\overrightarrow{ v }_{ O / m }\right)$
$ \overrightarrow{ v }_1-\overrightarrow{ v }_{ m }=-\frac{1}{4} \overrightarrow{ v }_0+\frac{1}{4} \overrightarrow{ v }_{ m }$
$ \overrightarrow{ v }_0=15 \, cm / s \hat{ i } $
$ \overrightarrow{ v }_{ I }=\overrightarrow{0 } cm / s $
$ \frac{5}{4} \overrightarrow{ v }_{ m }=\frac{\overrightarrow{ v }_0}{4}$
$ \overrightarrow{ v }_{ m }=\frac{\overrightarrow{ v }_0}{4}=\frac{15 cm / s \hat{ i }}{5}=3 m / s \hat{ i } $
$\left|\overrightarrow{ v }_{ m }\right|_{ m } cm / s =3$
A
If $r_B=\sqrt{\frac{3}{2}}$, then the electric field is zero everywhere outside $B$.
B
If $r_B=\frac{3}{2}$, then the electric potential just outside $B$ is $\frac{k}{\epsilon_0}$.
C
If $r_B=2$, then the total charge of the configuration is $15 \pi k$.
D
If $r_B=\frac{5}{2}$, then the magnitude of the electric field just outside $B$ is $\frac{13 \pi k}{\epsilon_0}$.
Solution
$q _1=\int\limits_0^1 kr 4 \pi r ^2 dr =\frac{4 \pi k }{4}=\pi k$
$q _2=\int\limits_1^{ r } \frac{2 k }{ r } 4 \pi r ^2 dr =\frac{8 \pi k \left( r ^2-1^2\right)}{2} $
$q _2=4 \pi k \left[ r ^2-1\right]=4 \pi kr r ^2-4 \pi k $
$q _{ net }= q _1+ q _2 $
$=4 \pi kr ^2-3 \pi k$
$ q _{\text {net }}=\pi k \left[4 r ^2-3\right]$
(A) $E _{\text {net }}=0 \Rightarrow q _{\text {net }}=0 \Rightarrow r =\frac{\sqrt{3}}{2}$
(B) $ V =\frac{ kQ _{ net }}{ r }=\frac{1}{4 \pi \varepsilon_0} \frac{\pi k \left(4 r ^2-3\right)}{ r }$
$ V =\frac{ k }{4 \varepsilon_0}\left[4 r -\frac{3}{ r }\right] $
$ =\frac{ k }{4 \varepsilon_0}\left[4 \times \frac{3}{2}-\frac{3 \times 2}{3}\right]=\frac{ k }{\varepsilon_0}$
(C) $ q _{ net }=\pi k \left[4(2)^2-3\right] $
$ =13 \pi k $
(D) $E _2 =\frac{ kQ }{ r ^2} $
$=\frac{1}{4 \pi \varepsilon_0} \frac{\pi k \left(4 r ^2-3\right)}{ r ^2}$
$ =\frac{ k }{4 \varepsilon_0}\left[\frac{4\left(\frac{5}{2}\right)^2-3}{(5 / 2)^2}\right]$
$=\frac{ k }{25 \varepsilon_0}[25-3]=\frac{22}{25} \frac{ k }{\varepsilon_0}$
A
When a voltage source of $6 V$ is connected across A and B in both circuits, $P_1 < P_2$.
B
When a constant current source of $2 Amp$ is connected across A and B in both circuits, $P_1>P_2$.
C
When a voltage source of $6 V$ is connected across A and B in Circuit-1, $Q_1>P_1$.
D
When a constant current source of $2 Amp$ is connected across A and B in both circuits, $Q_2 < Q_1$
Solution
Case (i)
When both switches are open equivalent resistance in circuit 1
$R _{ C _1}=\frac{16}{11} \Omega$
Equivalent resistance in circuit 2
$R _{ C _2}=\frac{6}{11} \Omega$
For voltage source
$P =\frac{ V ^2}{ R } $
$ P \propto \frac{1}{ R } $
$R _{ C _1}> R _{ C _2} $
$ \Rightarrow P _2> P _1 \text { (Option (A) correct) }$
For constant current source
$P=i^2 R $
$P \propto R $
$ \Rightarrow P_1>P_2 \text { (Option (B) correct) }$
Case-II
When switch is closed
$R _{ C _1}^{\prime}=\frac{5}{11} \Omega$
$R _{ C _2}^{\prime}=\frac{1}{2} \Omega$
$R _{ C _1}^{\prime} < R _{ C _1}$
For voltage source
$P \propto \frac{1}{ R } \Rightarrow Q _1> P _1(\text { Option }( C ) \text { correct) }$
$\& R _{ C _1}^{\prime}> R _{ C _2}^{\prime}$
For current source $P \propto R$
$Q _1> Q _2$
A
If the surface of the bubble is a perfect heat insulator, then $\left(\frac{r_1}{r_2}\right)^5=\frac{P_{a 2}+\frac{2 S}{r_2}}{P_{a 1}+\frac{2 S}{r_1}}$
B
If the surface of the bubble is a perfect heat insulator, then the total internal energy of the bubble including its surface energy does not change with the external atmospheric pressure.
C
If the surface of the bubble is a perfect heat conductor and the change in atmospheric temperature is negligible, then $\left(\frac{r_1}{r_2}\right)^3=\frac{P_{a 2}+\frac{4 S}{r_2}}{P_{a 1}+\frac{4 S}{r_1}}$.
D
If the surface of the bubble is a perfect heat insulator, then $\left(\frac{T_2}{T_1}\right)^{\frac{5}{2}}=\frac{P_{a 2}+\frac{4 S}{r_2}}{P_{a 1}+\frac{4 S}{r_1}}$.
Solution

$P_{ gas }=P_{ a }+\frac{4 S}{r}$
$PV ^{\gamma}=$ constant [adiabatic process]
$\left( Pa _1+\frac{4 S }{ r _1}\right)\left(\frac{4}{3} \pi r _1^3\right)^{5 / 3}=\left( P _{ a _2}+\frac{4 S }{ r _2}\right)\left(\frac{4}{3} \pi r _2^3\right)^{5 / 3}$
$ \frac{r_1^3}{r_2^3}=\left(\frac{P_{a_2}+\frac{4 S}{r_2}}{P_{a_1}+\frac{4 S}{r_1}}\right) $
$ P^{1-y} T^y=$ constant
$ \left(P_{a_2}+\frac{4 S}{r_2}\right)^{1-5 / 3} T_2^{5 / 3}=\left(P_{a_1}+\frac{4 S}{r_1}\right)^{1-5 / 3} T_1^{5 / 3} $
$ \left(\frac{T_2}{T_1}\right)^{5 / 3}=\left(\frac{P_{a_1}+\frac{4 S}{r_1}}{P_{a_2}+\frac{4 S}{r_2}}\right)^{-2 / 3} $
$ \left(\frac{T_2}{T_1}\right)^{5 / 2}=\left(\frac{P_{a_2}+\frac{4 S}{r_2}}{P_{a_1}+\frac{4 S}{r_1}}\right)$
A
For $\beta=\frac{1}{4}$ and $z_0=\frac{25}{7} R$, the particle reaches the origin.
B
For $\beta=\frac{1}{4}$ and $z_0=\frac{3}{7} R$, the particle reaches the origin.
C
For $\beta=\frac{1}{4}$ and $z_0=\frac{R}{\sqrt{3}}$, the particle returns back to $z=z_0$.
D
For $\beta>1$ and $z_0>0$, the particle always reaches the origin.
Solution
$W _{ el }+ W _{ ext }= k _{ f }- k _{ i }$
$qv _{ i }- qv _{ f }+ W _{ ext }= k _{ f }- k _{ i } $
$ \frac{ q \sigma}{2 \epsilon_0}\left[\sqrt{ R ^2+ Z ^2}- Z \right]-\frac{ q \sigma R }{2 \epsilon_0}+ CZ = k _{ f }-0 $
$ C =\frac{ q \sigma B }{2 \epsilon_0}$
Substitute $\beta \& Z$, calculate kinetic energy at $Z =0$
If kinetic energy is positive, then particle will reach at origin
If kinetic energy is negative, then particle will not reach at origin.
A
The phase difference between the two rays is independent of $d$.
B
The two rays interfere constructively at the detector.
C
The phase difference between the two rays depends on $n _1$ but is independent of $n_2$.
D
The phase difference between the two rays vanishes only for certain values of $d$ and the angle of incidence of the beam, with $\theta$ being the corresponding angle of refraction.
Solution

Optical path difference $\rightarrow$
$ \Delta x = n _1( d \tan \theta) \sin \alpha- n _2( d \tan \theta) \sin \theta $
$ =\left( n _1 \sin \alpha- n _2 \sin \theta\right) d \tan \theta $
$ =0 $
$ \Rightarrow \Delta \phi=0$
A
The magnitude of the total work done in the process $A \rightarrow B \rightarrow C$ is $144 \,kJ$.
B
The magnitude of the work done in the process $B \rightarrow C$ is $84\, kJ$.
C
The magnitude of the work done in the process $A \rightarrow B$ is $60 \,kJ$.
D
The magnitude of the work done in the process $C \rightarrow A$ is zero.
Solution
For adiabatic process $( A \rightarrow B )$
$ P _{ A } V _{ A }^\gamma= P _{ B } V _{ B }^\gamma$
$ 10^5 \times(0.8)^{\frac{5}{3}}=3 \times 10^5\left( V _{ B }\right)^{\frac{5}{3}}$
$ \Rightarrow V _{ B }=0.8 \times\left(\frac{1}{3}\right)^{0.6}=0.4$
Work done in process $A \rightarrow B$
$ W _{ AB }=\frac{ P _{ A } V _{ A }- P _{ B } V _{ B }}{\gamma-1} $
$\Rightarrow W _{ AB }=\frac{10^5 \times 0.8-3 \times 10^5 \times 0.4}{\frac{5}{3}-1} $
$\Rightarrow W _{ AB }=-60 kJ =\Rightarrow\left| W _{ AB }\right|=60 kJ$
Work done in process B $\rightarrow C$ (Isothermal process)
$W _{ BC }= nRT \ell n \frac{ V _{ C }}{ V _{ B }}= P _{ B } V _{ B } \ell n \frac{ V _{ C }}{ V _{ B }} $
$\Rightarrow W _{ BC }=3 \times 10^5 \times 0.4 \ell n \frac{0.8}{0.4} $
$ \Rightarrow W _{ BC }=84 kJ$
Work done in process $C \rightarrow A$
$W _{ CA }= P \Delta V =0 (\because \Delta V =0)$
So total work done in the process $A \rightarrow B \rightarrow C$
$ W _{ ABC }= W _{ AB }+ W _{ BC }+ W _{ CA }=-60+84+0 $
$ W _{ ABC }=24 kJ$
So correct options are (B,C,D)
A
2
B
5
C
$\frac{7}{2}$
D
$\frac{9}{2}$
Solution
$ v=\omega(2 R)$
$ v=\omega_0 R: $ no slipping
$ \therefore \omega_0=2 \omega$

$ \overrightarrow{ L }= m \overrightarrow{ r } \times \overrightarrow{ v }_{ c }+ I _{ c } \omega_0$
$ = M 2 Rv +\frac{1}{2} MR ^2 \omega_0$
$ =4 MR ^2 \omega+\frac{1}{2} MR ^2(2 \omega)=5 MR ^2 \omega$
$ \therefore n =5$
A
$1.72 \times 10^{-7} m , 1.20 \, eV$
B
$1.72 \times 10^{-7} m , 5.60 \,eV$
C
$3.78 \times 10^{-7} m , 5.60 \,eV$
D
$3.78 \times 10^{-7} m , 1.20 \, eV$
Solution
$ \frac{ hc }{\lambda}=\phi+6 \ldots \text { (i) } $
$ \frac{ hc }{4 \lambda}=\phi+0.6 \ldots \text { (ii) }$
$ \frac{3 hc }{4 \lambda}=5.4 eV \therefore \phi=1.2 eV$
$ \Rightarrow \frac{3}{4} \times \frac{6.63 \times 10^{-24} \times 3 \times 10^8}{5.4 \times 1.6 \times 10^{-19}}=\lambda=1.72 \times 10^{-7} m $
A
$2.22 \pm 0.02 mm , \pi(1.23 \pm 0.02) mm ^2$
B
$2.22 \pm 0.01 mm , \pi(1.23 \pm 0.01) mm ^2$
C
$2.14 \pm 0.02 mm , \pi(1.14 \pm 0.02) mm ^2$
D
$2.14 \pm 0.01 mm , \pi(1.14 \pm 0.01) mm ^2$
Solution
$LC =\frac{0.1}{100}=0.001 \,mm$
Zero error $=4 \times 0.001=0.004 \,mm$
Reading $1=0.5 \times 4+20 \times 0.001-0.004=2.16 \,mm$
Reading $2=0.5 \times 4+16 \times 0.001-0.004=2.12\, mm$
Mean value $=2.14 mm$
Mean absolute error $=\frac{0.02+0.02}{2}=0.02$
Diameter $=2.14 \pm 0.02$
Area $=\frac{\pi}{4} d ^2$
A
$\vec{B}=\frac{-\mu_0 I}{L}\left(\frac{3}{2}+\frac{1}{4 \sqrt{2} \pi}\right) \hat{k}$
B
$\vec{B}=-\frac{\mu_0 I}{L}\left(\frac{3}{2}+\frac{1}{2 \sqrt{2} \pi}\right) \hat{k}$
C
$\vec{B}=\frac{-\mu_0 I}{L}\left(1+\frac{1}{4 \sqrt{2} \pi}\right) \hat{k}$
D
$\vec{B}=\frac{-\mu_0 I}{L}\left(1+\frac{1}{4 \pi}\right) \hat{k}$
Solution
$\overrightarrow{ B }=\frac{\mu_0 I }{4 \pi L } \sin 45^{\circ}(-\hat{ k })+\frac{\mu_0 I \pi}{4 \pi \frac{ L }{2}}(-\hat{ k })+\frac{\mu_0 I }{4 \pi \frac{ L }{4}} \times \frac{\pi}{2}(-\hat{ k })$
JEE Advanced Chemistry Question Paper with Solution JE Advanced 2022 Paper 2
Answer: 6
Solution


$K _{ a _2}=1.2 \times 10^{-2}=\frac{(1- x )\left(1.8 \times 10^{-2}- x \right)}{(1+ x )}$
Since $x$ is very small $(1+x) \simeq 1$ and $(1-x) \simeq 1$
$x =\left(1.8 \times 10^{-2}-1.2 \times 10^{-2}\right) M$
$\left[ SO _4^{2-}\right]=\left(1.8 \times 10^{-2}-0.6 \times 10^{-2}\right) M $
$=1.2 \times 10^{-2} M$

$K _{ sp }= s \left( s +1.2 \times 10^{-2}\right)=1.6 \times 10^{-8} $
$\left( PbSO _4\right)$
Here, $\left( s +1.2 \times 10^{-2}\right) \simeq 1.2 \times 10^{-2}($ since ' $s$ ' is very small)
$ s\left(1.2 \times 10^{-2}\right)=1.6 \times 10^{-8}$
$ \Rightarrow s=\frac{1.6}{1.2} \times 10^{-6} M = X \times 10^{- Y } M$
$\Rightarrow Y =6$
Answer: 5
Solution
$0.1$ mole ionic salt in $1.8 \,kg$ water at $35^{\circ} C$
Vapour pressure of solution $=59.724\, mm$ of $Hg$
Vapour pressure of pure $H _2 O =60.000\, mm$ of $Hg$
Let the number of ions present per formula unit of the ionic salt be ' $x$
'

Moles of water $=\frac{1.8 \times 10^3}{18}=100$ moles
Relative lowering of vapour pressure $\frac{ P ^{\circ}- P _s}{ P ^{\circ}}=$ Mole fraction of non - volatile particles
$ \frac{ P ^{\circ}- P _s}{ P _{ s }}=\frac{\text { moles of non }-\text { volatileparticles }}{\text { moles of water }}$
$ \frac{60.000-59.724}{59.724}=\frac{0.01+0.09 x }{100} $
$ (0.276) \times 100=0.59274+(0.59274 \times 9) x$
$ 27.6-0.59274=(0.59274 \times 9) x$
$ \Rightarrow x \simeq \frac{27}{0.6 \times 9}=5$
Answer: 7
Solution
$ \Lambda^{\circ}\left(U_{ m } Y _{ p }\right) = m \times \lambda_{ u ^p}^0+ p \times \lambda_{ Y ^{+-}}^0=250 $
$ 25 m +100 p =250$
$ m +4 p =10....$(1)
$ \Lambda^{\circ}\left(V_{ m } X _{ n }\right)= m \times \lambda_{ v ^{2+}}+ n \times \lambda_{ x ^{m-}}^0=440$
$ 100 m +80 n =440$
$ 5 m +4 n =22....$(2)

From the extrapolation of curve
$\Lambda^{\circ}\left(Z_{ m } X _{ n }\right)=340 $
$ m \times \lambda_{ z ^{n+}}^{\circ}+ n \lambda_{ x ^{m-}}^{\circ}=340 $
$50 m +80 n =340 $
$ 5 m +8 n =34.....$(3)
(3) - (2) $\Rightarrow 4 n =12 \Rightarrow n =3$
Putting in (2) we get $m =2$
Putting in (1) we get $p =2$
$m + n + p =2+3+2=7$
Answer: 4
Solution
$ Xe +2 O _2 F _2 \rightarrow XeF _4+2 O _2 $
$ 3 XeF _4+6 H _2 O \rightarrow 2 Xe + XeO _3+\frac{3}{2} O _2+12 HF$
$\therefore$ One mole of $XeF _4$ gives 4 moles of HF on hydrolysis.
Answer: 6
Solution
$AgNO _3 \rightarrow 2 Ag +2 NO _2+1 / 2 O _2$
- Both $NO _2 \& O _2$ are paramagnetic
$- NO _2$ is odd electron molecule with one unpaired electron
$- O _2$ has two unpaired electrons

Total number of antibonding electrons $=6$
A
If empirical formula of compound 3 is $P _3 Q _4$, then the empirical formula of compound 2 is $P _3 Q _5$.
B
If empirical formula of compound 3 is $P _3 Q _2$ and atomic weight of element $P$ is 20 , then the atomic weight of $Q$ is 45 .
C
If empirical formula of compound 2 is $PQ$, then the empirical formula of the compound $1$ is $P _5 Q _4$
D
If atomic weight of $P$ and $Q$ are 70 and 35 , respectively, then the empirical formula of compound 1 is $P _2 Q$.
Solution
Compound
Weight % of P
Weight % of Q
1
50
50
2
44.4
55.6
3
40
60
For option (A)
Let atomic mass of $P$ be $M _{ P }$ and atomic mass of $Q$ be $M _{ Q }$ Molar ratio of atoms $P : Q$ in compound 3 is
$ \frac{40}{M_p}: \frac{60}{M_Q}=3: 4$
$\frac{2 M_Q}{3 M_p}=\frac{3}{4} \Rightarrow 9 M_p=8 M_Q$
Molar ratio of atoms $P : Q$ in compound 2 is
$ \frac{44.4}{M_p}: \frac{55.6}{M_Q} $
$=44.4 M _{ Q }: 55.6 M _{ P }$
$=44.4 M _{ Q }: 55.6 \times \frac{8 M _{ Q }}{9} $
$ =44.4: 55.6 \times \frac{8}{9}$
$=9: 10$
$\Rightarrow$ Empirical formula of compound 2 is therefore $P _9 Q _{10}$
Option (A) in incorrect
For option (B)
Molar Ratio of atoms $P: Q$ in compound 3 is $\frac{40}{ M _{ p }}: \frac{60}{ M _{ Q }}=3: 2$
$\frac{2 M _{ Q }}{3 M _{ p }}=\frac{3}{2} \Rightarrow 9 M _{ p }=4 M _{ Q }$
If $M _{ P }=20 \Rightarrow M _{ Q }=\frac{9 \times 20}{4}=45$
Option (B) is correct
For option (C)
Molar ratio of atoms $P : Q$ in compound 2 is
$ \frac{44.4}{M_p}: \frac{55.6}{M_Q}=44.4 M _Q: 55.6 M _{ p }=1: 1 $
$\Rightarrow \frac{ M _{ p }}{ M _{ Q }}=\frac{44.4}{55.6}$
Molar ratio of atoms $P$ : $Q$ in compound 1 is
$\frac{50}{ M _{ p }}: \frac{50}{ M _{ Q }}= M _{ Q }: M _{ p }$
$ =55.6: 44.4 $
$\simeq 5: 4$
Hence, empirical formula of compound 1 is $P _5 Q _4$
Hence, option $( C )$ is correct
For option (D)
Molar ratio of atoms P : Q in compound 1 is
$\frac{50}{ M _{ p }}: \frac{50}{ M _{ Q }} = M _{ Q }: M _{ p }$
$ =35: 70=1: 2$
Hence, empirical formula of compound 1 is $PQ _2$
Hence, option (D) is incorrect
| Compound | Weight % of P | Weight % of Q |
|---|---|---|
| 1 | 50 | 50 |
| 2 | 44.4 | 55.6 |
| 3 | 40 | 60 |
A
For the reaction, $M (s)+2 H ^{+}(a q) \rightarrow H _2(g)+ M ^{2+}(a q)$, if $\frac{ dE _{\text {cell }}}{ dT }=\frac{ R }{ F }$, then the entropy change of the reaction is $R$ (assume that entropy and internal energy changes are temperature independent).
B
The cell reaction, $Pt (s)\left| H _2(g, 1 bar )\right| H ^{+}(a q, 0.01 M ) \| H ^{+}(a q, 0.1 M )\left| H _2(g, 1 bar )\right| Pt (s)$, is an entropy driven process.
C
For racemization of an optically active compound, $\Delta S >0$.
D
$\Delta S >0$, for $\left[ Ni \left( H _2 O \right)_6\right]^{2+}+3 en \rightarrow\left[ Ni ( en )_3\right]^{2+}+6 H _2 O$ (where en $=$ ethylenediamine).
Solution
$\Delta G =\Delta H - T \Delta S$
$ \Delta G =\Delta H + T \left(\frac{ d \Delta G }{ dT }\right)_{ p } $
$- nF \left(\frac{ dE _{\text {cell }}}{ dT }\right)=-\Delta S $
$ \left.\frac{ dE _{\text {cell }}}{ dT }=\frac{\Delta S }{ nF }=\frac{ R }{ F } \text { (given }\right)$
$ \Rightarrow \Delta S = nR$
For the reaction, $M ( g )+2 H ^{\oplus}( aq ) \longrightarrow H _2( g )+ M ^{2 \oplus}( aq )$
$ n =2$
$\Rightarrow \Delta S =2 R$
Hence, option (A) is incorrect
For the reaction, $Pt _{( s )} \mid H _{2( g )}, 1$ bar $\left| H ^{\oplus}{ }_{ aq }(0.01 M )\right|\left| H ^{\oplus}( aq , 0.1 M )\right| H _2( g , 1 bar ) \mid Pt _{( s )}$
$E _{\text {cell }}= E _{\text {cell }}^{\circ}-\frac{0.0591}{1} \log \frac{0.01}{0.1}=0.0591 V$
$E_{cell}$ is positive $\Rightarrow \Delta G <0$ and $\Delta S >0(\Delta H =0$ for concentration cells $)$
Hence, option (B) is correct
Racemization of an optically active compound is a spontaneous process.
Here, $\Delta H =0$ (similar type of bonds are present in enantiomers)
$\Rightarrow \Delta S >0$
Hence, option (C) is correct.
$\left[ Ni \left( H _2 O \right)_6\right]^{2+}+3 en \rightarrow\left[ Ni ( en )_3\right]^{2+}+6 H _2 O$ is a spontaneous process
more stable complex is formed
$\Rightarrow \Delta S >0$
A
$B$
B
$B _2 H _6$
C
$B _2 O _3$
D
$HBF _4$
Solution
(A) $2 B +2 NH _3 \rightarrow 2 BN +3 H _2$
Boron produced BN with ammonia but Boron is element not compound. So that this option not involve in answer.
(B) $3 B _2 H _6+6 NH _3 \rightarrow 3\left[ BH _2\left( NH _3\right)_2\right]^{+}\left[ BH _4^{-}\right] \xrightarrow{ T =200^{\circ} C } 2 B _3 N _3 H _6+12 H _2$ $B _3 N _3 H _6 \xrightarrow{ T >200^{\circ} C }( BN )_{ x }$
(C) $B _2 O _3(\ell)+2 NH _3 \xrightarrow{1200^{\circ} C } 2 BN _{( s )}+3 H _2 O _{( g )}$
(D) $HBF _4+ NH _3 \rightarrow NH _4\left[ BF _4\right]$
A
Limestone is used to remove silicate impurity.
B
Pig iron obtained from blast furnace contains about $4 \%$ carbon.
C
Coke (C) converts $CO _2$ to $CO$.
D
Exhaust gases consist of $NO _2$ and $CO$.
Solution
(A) $CaO + SiO _2 \rightarrow CaSiO _3$ (in the temperature range $900-1500 K$ )
(B) In fusion zone molten iron becomes heavy by absorbing elemental impurities and produces Pig iron. (in the temperature range $900-1500 K$ )
(C) $C + CO _2 \rightarrow 2 CO$ (in the temperature range $900-1500 K$ )
(D) Exhaust gases does not contain $NO _2$.
A
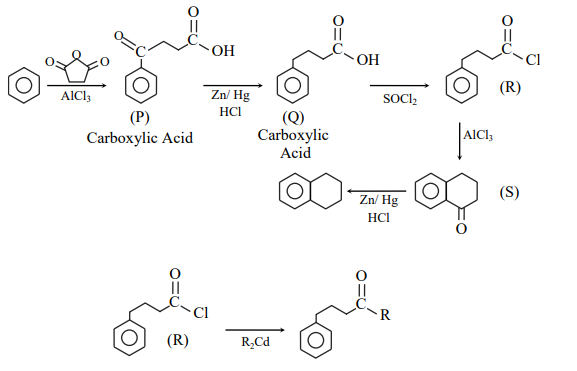
Compounds $P$ and $Q$ are carboxylic acids.
B
Compound $S$ decolorizes bromine water.
C
Compounds $P$ and $S$ react with hydroxylamine to give the corresponding oximes.
D
Compound $R$ reacts with dialkylcadmium to give the corresponding tertiary alcohol.
A
The polymerization of chloroprene gives natural rubber.
B
Teflon is prepared from tetrafluoroethene by heating it with persulphate catalyst at high pressures.
C
PVC are thermoplastic polymers.
D
Ethene at 350-570 K temperature and 1000-2000 atm pressure in the presence of a peroxide initiator yields high density polythene.
Solution
(a) The polymerisation of neoprene gives natural rubber.
(b) is correct statement
(c) is correct statement
(d) Ethene at $350-570 \,K$ temperature and $1000-2000$ atm pressure in the pressure of a peroxide initiator yields low density polythene.
A
25
B
35
C
55
D
75
Solution
Atom ' $X$ ' occupies FCC lattice points as well as alternate tetrahedral voids of the same lattice $\Rightarrow \frac{1}{4}$ th distance of body diagonal
$ =\frac{\sqrt{3} a}{4}=2 r_x $
$\Rightarrow a =\frac{8 r_x}{\sqrt{3}}$
Number of atoms of $X$ per cell
$ \underset{\text{(FCC lattice points)}}{=4} + \underset{\text{(Alternate tetrahedral voids)}}{4 } = 8$
$\% $ packing efficiency $ =\frac{\text { Volume occupied by } X }{\text { Volume of cubic unit cell }} \times 100 $
$ =\frac{8 \times \frac{4}{3} \pi\left( r _{ x }\right)^3}{ a ^3} \times 100$
$ =\frac{8 \times \frac{4}{3} \pi\left( r _{ x }\right)^3}{\left(\frac{\left.8 r _{ x }\right)^3}{\sqrt{3}}\right)} \times 100$
$=\left(8 \times \frac{4}{3} \times \pi \times \frac{1}{8^3} \times 3 \sqrt{3}\right) \times 100$
$ =\frac{\sqrt{3} \pi}{16} \times 100 $
$ =34 \%$
A
$Cl _2 O$
B
$ClO _2$
C
$Cl _2 O _6$
D
$Cl _2 O _7$
Solution
$ HClO _3+ HCl \rightarrow \underset{\text { (Paramagnetic) }}{ ClO _2}+\frac{1}{2} Cl _2+ H _2 O $
$ 2 ClO _2+2 O _3 \rightarrow Cl _2 O _6+2 O _2$
A
$PbCl _2$
B
$PbCl _4$
C
$\left[ PbCl _4\right]^{2-}$
D
$\left[ PbCl _6\right]^{2-}$
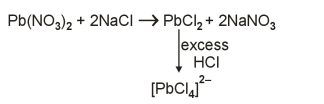
A
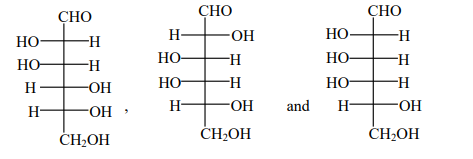
B
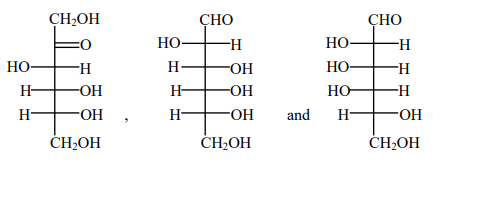
C
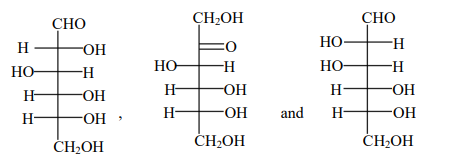
D
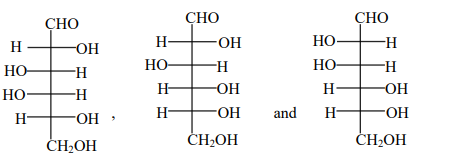
Solution
Basic catalyse tautomerism through enediol intermediate
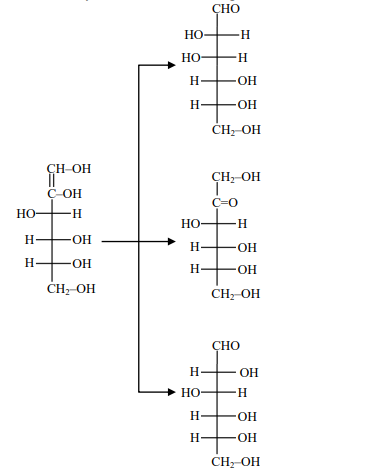
JEE Advanced Mathematics Question Paper with Solution JE Advanced 2022 Paper 2
Answer: 1
Solution
$ \alpha \in\left(0, \frac{\pi}{4}\right), \beta \in\left(-\frac{\pi}{4}, 0\right) \Rightarrow \alpha+\beta \in\left(-\frac{\pi}{4}, \frac{\pi}{4}\right) $
$ \sin (\alpha+\beta)=\frac{1}{3}, \cos (\alpha-\beta)=\frac{2}{3} $
$ \left(\frac{\sin \alpha}{\cos \beta}+\frac{\cos \alpha}{\sin \beta}+\frac{\cos \beta}{\sin \alpha}+\frac{\sin \beta}{\cos \alpha}\right)^2$
$ \left(\frac{\cos (\alpha-\beta)}{\cos \beta \sin \beta}+\frac{\cos (\beta-\alpha)}{\sin \alpha \cos \alpha}\right)^2 $
$ =4 \cos ^2(\alpha-\beta)\left(\frac{1}{\sin 2 \beta}+\frac{1}{\sin 2 \alpha}\right)^2 $
$ =4 \cos ^2(\alpha-\beta)\left(\frac{2 \sin (\alpha+\beta) \cos (\alpha-\beta)}{\sin 2 \alpha \sin 2 \beta}\right).....$(1)
$ =\frac{16 \cos ^4(\alpha-\beta) \sin ^2(\alpha+\beta) \times 4}{(\cos 2(\alpha-\beta)-\cos 2(\alpha+\beta))^2} $
$ =\frac{64 \cos ^4(\alpha-\beta) \sin ^2(\alpha+\beta)}{\left(2 \cos ^2(\alpha-\beta)-1-1+2 \sin ^2(\alpha+\beta)\right)^2} $
$ =64 \times \frac{16}{81} \times \frac{1}{9} \frac{1}{\left(2 \times \frac{4}{9}-1-1+\frac{2}{9}\right)^2}$
$ =\frac{64 \times 16}{81 \times 9} \cdot \frac{81}{64}=\frac{16}{9} $
$ {\left[\frac{16}{9}\right]=1 \text { Ans. }}$
Answer: 8
Solution
$ x d y-\left(y^2-4 y\right) d x=0, x>0$
$ \int \frac{d y}{y^2-4 y}=\int \frac{d x}{x} $
$\int\left(\frac{1}{y-4}-\frac{1}{y}\right) d y=4 \int \frac{d x}{x}$
$ \log _c|y-4|-\log _c|y|=4 \log _e x+\log _e c$
$ \frac{| y -4|}{| y |}= cx ^4 \xrightarrow{(1,2)} c =1 $
$|y-4|=|y| x^4 $
$ C -1 $
$ y-4=y x^4$
$ y=\frac{4}{1-x^4}$
$y(1)=\text { ND (rejected) } $
$C-2$
$ y-4=-y x^4 $
$ y=\frac{4}{1+x^4} $
$ y(1)=2$
$ y (\sqrt{2})=\frac{4}{5} \Rightarrow 10 y (\sqrt{2})=8 $
Answer: 5
Solution
$ f ( x )=\log _2\left( x ^3+1\right)= y$
$x ^3+1=2^y \Rightarrow x =\left(2^y-1\right)^{1 / 3}= f ^{-1}( y ) $
$ f ^{-1}( x )=\left(2^{ x }-1\right)^{1 / 3}$
$ =\int_1^2 \log _2\left( x ^3+1\right) dx +\int\limits_1^{\log _2 9}\left(2^x-1\right)^{1 / 3} dx$
$ =\int_1^2 f ( x ) dx +\int\limits_1^{\log _2 9} f ^{-1}( x ) dx =2 \log _2 9-1 $
$ =8<9<2^{7 / 2} \Rightarrow 3<\log _2 9<\frac{7}{2}$
$ =5<2 \log _2 9-1<6 $
$ {\left[2 \log _2 9-1\right]=5}$
Answer: 1
Solution
$x^{16\left(\log _5 x\right)^3-68 \log _5 x}=5^{-16}$
Take $\log$ to the base 5 on both sides and put $\log _5 x=t$
$16 t ^4-68 t ^2+16=0 $
$ \Rightarrow 4 t ^4-17 t ^2+4=0 \begin{cases} t _1 \\t _2 \\t _3 \\t _4\end{cases} $
$ t _1+ t _2+ t _3+ t _4=0$
$ \log _5 x _1+\log _5 x _2+\log _5 x _3+\log _5 x _4=0$
$ x_1 x_2 x_3 x_4=1$
Answer: 5
Solution
$\beta=\displaystyle\lim _{x \rightarrow 0} \frac{e^{x^3}-\left(1-x^3\right)^{1 / 3}}{\frac{x \sin ^2 x}{x^2} x^2}+\frac{\left(\left(1-x^2\right)^{1 / 2}-1\right) \sin x}{x \frac{\sin ^2 x}{x^2} x^2}$
use expansion
$ \beta=\displaystyle\lim _{x \rightarrow 0} \frac{\left(1+x^3\right)-\left(1-\frac{x^3}{3}\right)}{x^3}+\displaystyle\lim _{x \rightarrow 0} \frac{\left(\left(1-\frac{x^2}{2}\right)-1\right)}{x^2} \frac{\sin x}{x} $
$ \beta=\displaystyle\lim _{x \rightarrow 0} \frac{4 x^3}{3 x^3}+\displaystyle\lim _{x \rightarrow 0} \frac{-x^2}{2 x^2}$
$ \beta=\frac{4}{3}-\frac{1}{2}=\frac{5}{6}$
$ 6 \beta=5$
Answer: 3
Solution
$ A=\begin{pmatrix}\beta & 0 & 1 \\ 2 & 1 & -2 \\ 3 & 1 & -2\end{pmatrix}|A|=-1 $
$ \Rightarrow\left|A^7-(\beta-1) A^6-\beta A^5\right|=0 $
$\Rightarrow|A|^5\left|A^2-(\beta-1) A-\beta I\right|=0$
$\Rightarrow|A|^5\left|\left(A^2-\beta A \right)+A-\beta I\right|=0$
$\Rightarrow|A|^5|A(A-\beta I)+I(A-\beta I)|=0$
$|A|^5|(A+I)(A-\beta I)|=0$
$ A+I=\begin{pmatrix}\beta+1 & 0 & 1 \\ 2 & 2 & -2 \\ 3 & 1 & -1\end{pmatrix} \Rightarrow|A+I|=-4$,
Here $| A | \neq 0 \&|A+I| \neq 0 $
$ A-\beta I=\begin{pmatrix}0 & 0 & 1 \\ 2 & 1-\beta & -2 \\ 3 & 1 & -2-\beta\end{pmatrix} $
$ |A-\beta I|=2-3(1-\beta)=3 \beta-1=0 \Rightarrow \beta=\frac{1}{3} $
$ 9 \beta=3$
Answer: 7
Solution

$ S P- PP =20$
$ \beta-\frac{\delta}{\sin \frac{\alpha}{2}}=20$
$ \beta^2+\frac{\delta^2}{\sin ^2 \frac{\alpha}{2}}-400=\frac{2 \beta \delta}{\sin \frac{\alpha}{2}} $
$ \frac{1}{ SP }=\frac{\sin \frac{\alpha}{2}}{\delta} $
$\cos \alpha=\frac{ SP ^2+\beta^2-656}{2 \beta \frac{\delta}{\sin \frac{\alpha}{2}}}$
$ =\frac{\frac{2 \beta \delta}{\sin \frac{\alpha}{2}}-256}{\frac{2 \beta S}{\sin \frac{\alpha}{2}}}=\cos \alpha$
$ \frac{\lambda-128}{\lambda}=\cos \alpha$
$ \lambda(1-\cos \alpha)=128$
$\frac{\beta \delta}{\sin \frac{\alpha}{2}} \cdot 2 \sin ^2 \frac{\alpha}{2}=128 $
$ \frac{\beta \delta}{9} \sin \frac{\alpha}{2}=\frac{64}{9} $
$\Rightarrow\left[\frac{\beta \delta}{9} \sin \frac{\alpha}{2}\right]=7 $ where [.] denotes greatest integer function
Answer: 6