JEE Main Physics Question Paper with Solution 2023 January 31st Shift 2 - Evening
A
A - IV, B - II, C - I, D - III
B
A - II, B - III, C - IV, D - I
C
A - III, B - I, C - IV, D - II
D
A - I, B - IV, C - III, D - II
A
$1: 4$
B
$1: 1$
C
$3=10$
D
$1: 2$
A
$3.14 \Omega$
B
$6.28 S$
C
$0.318 \Omega$
D
$0.5 \Omega$
A
Net potential of the system cannot be zero at a point but net electric field can be zero at that point.
B
Net potential of the system at a point can be zero but net electric field can't be zero at that point.
C
Both the net potential and the net electric field cannot be zero at a point.
D
Both the net potential and the net field can be zero at a point.
A
$3.65 \times 10^3 \,ms ^{-1}$
B
$18.96 \times 10^3 \, ms ^{-1}$
C
$145.75 \times 10^3 \, ms ^{-1}$
D
$6.32 \times 10^3 \, ms ^{-1}$
A
$n : N$
B
$N : n$
C
$N ^2: n ^2$
D
$n^2: N ^2$
A
$\frac{ R }{3}$
B
$9 R$
C
$2.25 R$
D
$3 R$
Solution
$
r =0.529 \times \frac{ n ^2}{ z }
$
$
r \propto n^2
$
$
R \propto(2)^2
$
$
R_1 \propto(3)^2
$
Divide (1) by (2)
$
\frac{ R _1}{ R }=\frac{4}{9}
$
$
R _1=\frac{9 R }{4}
$
$
R _1=2.25 R
$
A
Both metals A and B will emit photo-electrons
B
Metal B will not emit photo-electrons
C
Both metals A and B will not emit photo-electrons
D
Metal A will not emit photo-electrons
A
Statement I is correct but Statement II is incorrect
B
Both Statement I and Statement II are incorrect
C
Both Statement I and Statement II are correct
D
Statement I is incorrect but Statement II is correct
A
A - IV, B - I, C - II, D - III
B
A - II, B - IV, C - III, D - I
C
A - IV, B - III, C - I, D - II
D
A - III, B - II, C - I, D - IV
A
Both Statement I and Statement II are incorrect
B
Statement I is correct but Statement II is incorrect
C
Both Statement I and Statement II are correct
D
Statement I is incorrect but Statement II is correct
A
$40 \,ms ^{-1}$
B
$20\, ms ^{-1}$
C
$400\, ms ^{-1}$
D
$10 \,ms ^{-1}$
A
$\frac{ W }{100}$
B
$\frac{ W }{3}$
C
$\frac{W}{91}$
D
$\frac{W}{9}$
A
$\frac{3}{1}$
B
$\frac{3}{2}$
C
$\frac{1}{2}$
D
$\frac{4}{3}$
JEE Main Chemistry Question Paper with Solution 2023 January 31st Shift 2 - Evening
A
Copper gauze
B
$Pd$
C
$Ni$
D
Copper oxide
Solution
Duma's method.
The nitrogen containing organic compound, when heated with $CuO$ in a atmosphere of $CO _2$, yields free $N _2$ in addition to $CO _2$ and $H _2 O$.
$C _{ x } H _{ y } N _{ z }+\left(2 x +\frac{ y }{2}\right) CuO \rightarrow$
$ x CO _2+\frac{ y }{2} H _2 O +\frac{ z }{2} N _2+\left(2 x +\frac{ y }{2}\right) Cu$
Traces of nitrogen oxides formed, if any, are reduced to nitrogen by passing the gaseous mixture over heated copper gauze.
A
$C _{11} H _8$
B
$C _{11} H _4$
C
$C _5 H _8$
D
$C _9 H _8$
Solution
$ C _{ x } H _{ y }+\left( x +\frac{ y }{4}\right) O _2 \rightarrow xCO _2+\frac{ y }{2} H _2 O $
$ \frac{ y }{2}=4 \therefore y =8 $
$ x +\frac{8}{4}=11 $
$ \therefore x =9 $
$ \therefore $ Hydrocarbon will be$= C _9 H _8$
A
Methyl orange may be used for a weak acid vs weak base titration.
B
. Phenolphthalein may be used for a strong acid vs strong base titration.
C
Methyl orange is a suitable indicator for a strong acid vs weak base titration.
D
Phenolphthalein is a suitable indicator for a weak acid vs strong base titration.
Solution
Indicator $\,\,\, \,\,\,\,\,\,\,$ pH range
Methyl orange $\,\,\, $3.2 - 4.5
Phenolpthalein $\,\,\, $8.3 - 10.5
Methyl orange may be used for a strong acid vs
strong base and strong acid vs weak base titration.
Phenolpthalein may be used for a strong acid vs
strong base and weak acid vs strong base titration
A
$D > B > C > A$
B
$B > D > C > A$
C
$A > C > B > D$
D
$D > B > A > C$
Solution
(A) $n =3 ; l =0 ; m =0 ; 3 s$ orbital
(B) $n =4 ; l =0 ; m =0 ; 4 s$ orbital
(C) $n =3 ; l =1 ; m =0 ; 3 p$ orbital
(D) $n =3 ; l =2 ; m =0 ; 3 d$ orbital
As per Hund's rule energy is given by $( n +l)$ value. If value of $( n +l)$ remains same then energy is given by n only.
A
A, B, E
B
C, D
C
A, B
D
B, D, E
Solution
Veronal is neurological medicine, Prontosil is antibiotic, rest all are disinfectants
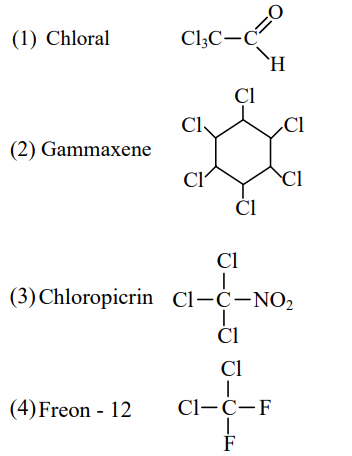
A
Chloral
B
Gammaxene
C
Chloropicrin
D
Freon-12
A
Both $( A )$ and $( R )$ are true and $( R )$ is the correct explanation of $( A )$
B
(A) is true but (R) is false
C
(A) is false but (R) is true
D
Both $( A )$ and $( R )$ are true but $( R )$ is not the correct explanation of $( A )$
Solution
From $Sc$ to $Mn$ ionization energy is less than that of $Mg$.
For $3d$ series :
Sc
Ti
V
Cr
Mn
IE (KJ/mol)
631
656
650
653
717
Fe
Co
Ni
Cu
Zn
IE (KJ/mol)
762
758
736
745
906
For $2^\text{nd}$ Group
Be
Mg
Ca
Sr
Ba
Ra
IE (KJ/mol)
631
656
650
653
717
762
| Sc | Ti | V | Cr | Mn | |
| IE (KJ/mol) | 631 | 656 | 650 | 653 | 717 |
| Fe | Co | Ni | Cu | Zn | |
| IE (KJ/mol) | 762 | 758 | 736 | 745 | 906 |
| Be | Mg | Ca | Sr | Ba | Ra | |
| IE (KJ/mol) | 631 | 656 | 650 | 653 | 717 | 762 |
A
A - III, B - IV, C - I, D - II
B
A - II, B - III, C - I, D - IV
C
A - II, B - I, C - IV, D - III
D
A - IV, B - II, C - III, D - I
Solution
(A) Physisorption =$ 20 - 40$ kJ/mol and
Chemisorption = $80 - 240$ kJ/mol
(B) Physisorption is multi-layered and
chemisorption is unimolecular layered.
(C) In heterogeneous catalysis, medium and
catalyst are in different phases.
(D) Chromatography uses adsorption to
purify/separate mixtures
A
B and D only
B
B, D and E only
C
A and C only
D
A, B and D only
Solution
(A) $\Delta T_b \propto i \times c$
(B) Azeotropic mixtures have same composition in both liquid and vapour phase.
(C) Osmosis always takes place from hypotonic to hypertonic solution.
(D) $M =\frac{30 \times 10 \times 1.26}{98} \approx 4.09 M$
(E) When $KI$ solutions is added to $AgNO _3$ solution, positively charged solution results due to adsorption of $Ag ^{\circ}$ ions from dispersion medium
$AgI / Ag ^{+}$
Positively charged
A
Both Statement I and Statement II are false
B
Both Statement I and Statement II are rue
C
Statement I is false but Statement II is true
D
Statement I is true but Statement II is false
Solution
(Borax Bead Test)
On treatment with metal salt, boric anhydride
forms metaborate of the metal which gives
different colours in oxidising and reducing flame.
For example, in the case of copper sulphate,
following reactions occur.
$CuSO _4+ B _2 O _3 \xrightarrow[(\text { Oxidising ) }] {\text { Non -luminous flame }} \underset{\text{Cupric metaborate blue-green}}{Cu \left( BO _2\right)_2+ SO _3}$
Two reactions may take place in reducing flame (Luminous flame)
(i) The blue-green $Cu \left( BO _2\right)_2$ is reduced to colourless cuprous metaborate as :
$2 Cu \left( BO _2\right)_2+2 NaBO _2+ C \xrightarrow[\text { flame }]{\text { Luminous }} $
$2 CuBO _2+ Na _2 B _4 O _7+ CO$
(ii) Cupric metaborate may be reduced to metallic copper and bead appears red opaque.
$ 2 Cu \left( BO _2\right)_2+4 NaBO _2+2 C \xrightarrow[\text { flame}]
{\text { Luminous}}$
$ 2 Cu +2 Na _2 B _4 O _7+2 CO$
A
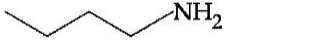
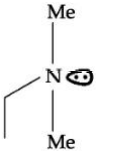
B
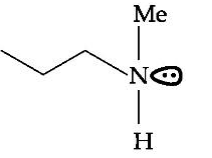
C
D
Solution
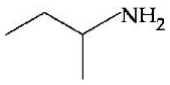
$C _4 H _{11} N$ releases $N _2$ with $HNO _2$ i.e. it is primary amine.
After reacting with Hinsberg reagent it forms a compound which is soluble in $KOH$, Hence, the amine is primary.
A
B
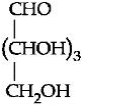
C
D
Solution
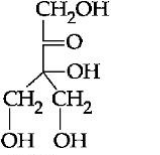
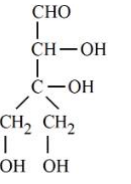
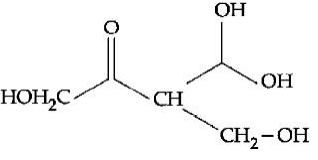
(i) Formation of tetraacetete with $Ac _2 O$ means compound $A$ has four $- OH$ linkage.
Reduction of A with $HI$ gives Isopentane i.e. molecule contains five carbon atom.
A
Statement I is correct but Statement II is incorrect
B
Both Statement I and Statement II are correct
C
Statement I is incorrect but Statement II is correct
D
Both Statement I and Statement II are incorrect
Solution
It is used in the synthesis of hydroquinone, tartaric acid and certain food products and pharmaceuticals (cephalosporin) etc. Restoration of aerobic conditions to sewage wastes etc
A
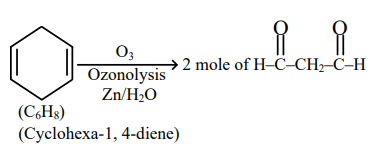
hexa-1, 3, 5-triene
B
1-methylcyclopenta-1, 4-diene
C
cyclohexa - 1, 3-diene
D
cyclohexa-1, 4-diene
A
A and B only
B
C and D only
C
B and D only
D
A and E only
Solution
1. ${ }_{62} Sm : 4\, f ^6\, 6 s ^2$
2. ${ }_{64} Gd : 4\, f ^7 \,5 d ^1\, 6 s ^2$
3. ${ }_{63} Eu : 4\, f ^7 \,6 s ^2$
4. ${ }_{65} Tb : 4\, f ^9 \,6 s ^2$
5. ${ }_1 Pm : 4 \,f ^5 \,6 s ^2$
A
$BCl _3> BF _3> BBr _3> BI _3$
B
$BI _3> BBr _3> BCl _3> BF _3$
C
$BBr _3> BI _3> BCl _3> BF _3$
D
$BF _3> BCl _3> BBr _3> BI _3$
Solution
Extent of back bonding, reduces down the group leading to more Lewis acidic strength
$\underset{ (2 p-2 p)}{ BF _3 }> \underset{(2 p-3 p)}{BCl _3} > \underset{(2 p-4 p)}{BBr _3} >\underset{(2 p-5 p) }{ BI _3} \text { (extent of back bonding) }$
$ BF _3< BCl _3< BBr _3< BI _3 \text { (lewis acidic nature) }$
A
$CO _2+ H _2 O \rightarrow H _2 CO _3$
B
$N _2 O _5+ H _2 O \rightarrow 2 HNO _3$
C
$2 SO _2+ O _2+2 H _2 O \rightarrow 2 H _2 SO _4$
D
$4 NO _2+ O _2+2 H _2 O \rightarrow 4 HNO _3$
Solution
We are aware that normally rain water has a $pH$ of $5.6$ due to the presence of $H ^{+}$ions formed by the reactions of rain water with carbon dioxide present in the atmosphere.
$ H _2 O ( l )+ CO _2( g ) \leftrightharpoons H _2 CO _3( aq )$
$H _2 CO _3( aq ) \leftrightharpoons H ^{+}( aq )+ HCO _3^{-}( aq ) $
A
van Arkel method is used to purify tungsten.
B
The malleable iron is prepared from cast iron by oxidising impurities in a reverberatory furnace.
C
Cast iron is obtained by melting pig iron with scrap iron and coke using hot air blast.
D
Boron and Indium can be purified by zone refining method.
Solution
Van - Arkel process is used for purification of $Ti, Zr, Hf $ and $B$ .
A
Be
B
$Mg$
C
Ca
D
$Li$
Solution
Calcium plays important role in neuromuscular function, interneuronal transmission, cell membrane etc.
Answer: 173
Solution
$ \Delta_{ r } H =\sum H _{ p }-\sum H _{ R } $
$ =(-394+4 \times-92)-(-105+(2 \times-242)) $
$ =-173 \,kJ / mol $
Answer: 480
Solution
$ \left( Ti ^{+3}\left( H _2 O \right)_6\right)^{3+} $
$ Ti ^{+3}: 3 d ^1$
$ \text { C.F.S.E. }=-0.4 \times \Delta_0$
$ =-\frac{96 \times 10^3}{ N _0} J $
$\Delta_0 =\frac{96 \times 10^3}{0.4 \times 6 \times 10^{23}} $
$ \Rightarrow \frac{ hc }{\lambda} =\frac{96 \times 10^3}{0.4 \times 6 \times 10^{23}} $
$ \lambda =\frac{0.4 \times 6 \times 10^{23} \times 6.4 \times 10^{-34} \times 3 \times 10^8}{96 \times 10^3} $
$ =0.48 \times 10^{-6} m $
$ =480 \times 10^{-9} m $
$ =480 \,nm$
Answer: 2
Solution
$K, Rb$ and $Cs$ form stable super oxides but $Cs$ has ionisation enthalpy less than $400 \,kJ$.
Answer: 10
Solution
$AgCl ( s ) \rightarrow \underset{S}{Ag ^{+}}$(aq.) $+ \underset{S}{Cl ^{-}}$(aq.)
$ K _{ sp }= S ^2=\left(\frac{1.43}{143.4} \times 10^{-3}\right)^2=10^{-10} $
$ -\log K _{ sp }=10$
Answer: 59
Solution

$ 2 x+3(0.83-x)=2 $
$ x=0.49 $
$ \% M^{2+}=\frac{0.49}{0.83} \times 100 $
$ =59 \%$
Answer: 17
Solution
$ C =\frac{ C _{ o }}{2^{ n }} =\frac{ C _{ o }}{32} $
$ n =5 $
$ t =5 t _{1 / 2} $
$ =\frac{5 \times 0.693}{20}=\frac{0.693}{4} $
$ =0.17325 \min =17.325 \times 10^{-2} \min $
Answer: 227
Solution
$\underset{\text{ 1 mol}}{2 C ( s )}+\underset{\text{1.5 mol}}{ O _2( g )} \rightarrow 2 CO ( g )$
Limiting reagent is carbon. One mole carbon produces one mole $CO$. Hence, volume at STP is $227 \times 10^{-1}$ litre
Answer: 25
Solution
$\Lambda_{ m }= \frac{\kappa \times 1000}{ M }$
$\Lambda_{ m }= \frac{1}{\rho} \times \frac{1000}{ M } $
$ \frac{1}{5 \times 10^{-3}} \times \frac{1000}{0.8}$
Ans. $25 \times 10^4 \,\Omega^{-1}\, cm ^{-2}\, mol ^{-1}$
JEE Main Mathematics Question Paper with Solution 2023 January 31st Shift 2 - Evening
A
$\frac{4}{6+\sqrt{\pi}}$
B
$\frac{8}{6+\sqrt{\pi}}$
C
$\frac{8}{\sqrt{\pi}}$
D
$\frac{4}{6-\sqrt{\pi}}$
Solution
$ \phi^{\prime}( x )=\frac{1}{\sqrt{ x }}\left[\left(4 \sqrt{2} \sin x -3 \phi^{\prime}( x )\right) \cdot 1-0\right]-\frac{1}{2} x ^{-3 / 2} $
$ \int\limits_{\frac{\pi}{4}}^{ x }\left(4 \sqrt{2} \sin t -3 \phi^{\prime}( t )\right) dt $
$ \phi^{\prime}\left(\frac{\pi}{4}\right)=\frac{2}{\sqrt{\pi}}\left[4-3 \phi^{\prime}\left(\frac{\pi}{4}\right)\right]+0$
$ \left(1+\frac{6}{\sqrt{\pi}}\right) \phi^{\prime}\left(\frac{\pi}{4}\right)=\frac{8}{\sqrt{\pi}}$
$ \phi^{\prime}\left(\frac{\pi}{4}\right)=\frac{8}{\sqrt{\pi}+6}$
A
64
B
$32 \sqrt{2}$
C
32
D
$16 \sqrt{2}$
Solution
$\left(3 y^2-5 x^2\right) y \cdot d x+2 x\left(x^2-y^2\right) d y=0$
$ \Rightarrow \frac{d y}{d x}=\frac{y\left(5 x^2-3 y^2\right)}{2 x\left(x^2-y^2\right)} $
Put $y=m x $
$\Rightarrow m+x \cdot \frac{d m}{d x}=\frac{m\left(5-3 m^2\right)}{2\left(1-m^2\right)}$
$x \cdot \frac{d m}{d x}=\frac{\left(5-3 m^2\right) m-2 m\left(1-m^2\right)}{2\left(1-m^2\right)}$
$\Rightarrow \frac{ dx }{ x }=\frac{2\left( m ^2-1\right)}{ m \left( m ^2-3\right)} dm$
$\Rightarrow \frac{ dx }{ x }=\left(\frac{2}{ m }-\frac{\frac{4}{3}}{ m }+\frac{\frac{4 m }{3}}{ m ^2-3}\right) dm$
$ \Rightarrow \int \frac{ dx }{ x }=\int \frac{\left(\frac{2}{3}\right)}{ m }+\int \frac{2}{3}\left(\frac{2 m }{ m ^2-3}\right) dm $
$ \Rightarrow \ln | x |=\frac{2}{3} \ln | m |+\frac{2}{3} \ln \left| m ^2-3\right|+ C $
$ \text { Or, } \ln | x |=\frac{2}{3} \ln \left|\frac{ y }{ x }\right|+\frac{2}{3} \ln \left|\left(\frac{ y }{ x }\right)^2-3\right|+ C $
$ \text { Put }( x =1, y =1): \text { we get } c =-\frac{2}{3} \ln (2)$
$ \Rightarrow \ln | x |=\frac{2}{3} \ln \left|\frac{ y }{ x }\right|+\frac{2}{3} \ln \left|\left(\frac{ y }{ x }\right)^2-3\right|-\frac{2}{3} \ln (2)$
$ \Rightarrow\left(\frac{ y }{ x }\right)\left[\left(\frac{ y }{ x }\right)^2-3\right]=2 .\left( x ^{3 / 2}\right)$
Put $x=2$ to get $y$ ( 2 )
$ \Rightarrow y \left( y ^2-12\right)=4 \times 2 \times 2 \times 2 \sqrt{2} $
$ \Rightarrow y ^3-12 y =32 \sqrt{2}$
$ \Rightarrow\left| y ^3(2)-12 y (2)\right|=32 \sqrt{2}$
A
$(0,4,4)$
B
$(3,0,4)$
C
$(0,6,3)$
D
$(2,2,4)$
Solution
Equation of Plane:
$ (2 \hat{ i }+ aj +4 \hat{ k }) \cdot[( x -2) \hat{ i }+( y - a ) \hat{ j }+( z -4) \hat{ k }]=0$
$ \Rightarrow 2 x + ay +4 z =20+ a ^2$
$ \Rightarrow A \equiv\left(\frac{20+ a ^2}{2}, 0,0\right) $
$ B \equiv\left(0, \frac{20+ a ^2}{ a }, 0\right) $
$ C \equiv\left(0,0, \frac{20+ a ^2}{4}\right)$
$\Rightarrow$ Volume of tetrahedron
$=\frac{1}{6}[\vec{a} \vec{b} \vec{c}]$
$ =\frac{1}{6} \vec{a} \cdot(\vec{b} \times \vec{c}) $
$ \Rightarrow \frac{1}{6}\left(\frac{20+ a ^2}{2}\right) \cdot\left(\frac{20+ a ^2}{ a }\right) \cdot\left(\frac{20+ a ^2}{4}\right)=144 $
$\Rightarrow\left(20+ a ^2\right)^3=144 \times 48 \times a$
$\Rightarrow a =2$
$\Rightarrow$ Equation of plane is $2 x +2 y +4 z =24$
Or $x+y+2 z=12$
$\Rightarrow(3,0,4)$ Not lies on the Plane $x+y+2 z=12$
A
$(8, \infty)$
B
$(0,4]$
C
$(4, \infty)$
D
$(2,12]$
Solution
$ x ^2+ y ^2-\frac{(1+ a ) x }{2}-\frac{(1- a ) y }{2}=0 $
$ \text { Centre }\left(\frac{1+ a }{4}, \frac{1- a }{4}\right) \Rightarrow( h , k )$
$P \left(\frac{1+ a }{2}, \frac{1- a }{2}\right) \Rightarrow(2 h , 2 k )$

Equation of chord $\Rightarrow T=S_1$
$ \Rightarrow( x - y ) \lambda-\frac{2 h ( x +\lambda)}{2}-\frac{(2 k )( y -\lambda)}{2}$
$ =2 \lambda^2-2 h (\lambda)+2 k \lambda$
Now, $\lambda(2 h , 2 k )$ satisfies the chord
$ \therefore(2 h -2 k ) \lambda- h ( x +\lambda)- k ( y -\lambda) $
$ \Rightarrow 2 \lambda^2+4 k \lambda-4 h \lambda+ h \lambda- k \lambda+ hx + ky =0 $
$ \Rightarrow 2 \lambda^2+\lambda(3 k -3 h )+ ky + hx =0 $
$ \Rightarrow D >0 $
$ \Rightarrow 9( k - h )^2-8( ky + hx )>0 $
$ \Rightarrow 9( k - h )^2-8\left(2 k ^2+2 h ^2\right)>0 $
$ \Rightarrow-7 k ^2-7 h ^2-18 kh >0 $
$ \Rightarrow 7 k ^2+7 h ^2+18 kh <0 $
$ \Rightarrow 7\left(\frac{1- a }{4}\right)^2+7\left(\frac{1+ a }{4}\right)^2+18\left(\frac{1- a ^2}{16}\right)<0$
$ \Rightarrow 7\left[\frac{2\left(1+ a ^2\right)}{16}\right]+\frac{18\left(1- a ^2\right)}{16}<0, a ^2= t$
$ \Rightarrow \frac{7}{8}(1+ t )+\frac{18(1- t )}{16}<0 $
$\Rightarrow \frac{14+14 t +18-18 t }{16}<0 $
$ \Rightarrow 4 t >32$
$ t >8 \,\,\,\,a ^2>8$
A
2
B
$2 \sqrt{2}$
C
4
D
$\sqrt{2}$
Solution
After rationalising
$ \int\limits_0^\alpha \frac{ x }{\alpha}(\sqrt{ x +\alpha}+\sqrt{ x }) $
$ \int\limits_0^\alpha \frac{1}{\alpha}\left[( x +\alpha)^{3 / 2}-\alpha( x +\alpha)^{1 / 2}+ x ^{3 / 2}\right]$
$ \left.\frac{1}{\alpha}\left[\frac{2}{5}( x +\alpha)^{5 / 2}-\alpha \frac{2}{3}( x +\alpha)^{3 / 2}+\frac{2}{5} x ^{5 / 2}\right]\right|_0 ^\alpha$
$ =\frac{1}{\alpha}\left(\frac{5}{2}(2 \alpha)^{5 / 2}-\frac{2 \alpha}{3}(2 \alpha)^{3 / 2}+\frac{2}{5} \alpha^{5 / 2}-\frac{2}{5} \alpha^{5 / 2}+\frac{2}{3} \alpha^{5 / 2}\right.$
$ =\frac{1}{\alpha}\left(\frac{2^{7 / 2} \alpha^{5 / 2}}{5} \frac{2^{5 / 2} \alpha^{5 / 2}}{3}+\frac{2}{3} \alpha^{5 / 2}\right) $
$ =\alpha^{3 / 2}\left(\frac{2^{7 / 2}}{5}-\frac{2^{5 / 2}}{3}+\frac{2}{3}\right) $
$ =\frac{\alpha^{3 / 2}}{15}(24 \sqrt{2}-20 \sqrt{2}+10)=\frac{\alpha^{3 / 2}}{15}(4 \sqrt{2}+10)$
Now,
$ \frac{\alpha^{3 / 2}}{15}(4 \sqrt{2}+10)=\frac{16+20 \sqrt{2}}{15}$
$ \Rightarrow \alpha=2$
A
$\frac{381}{4}$
B
9
C
$\frac{33}{4}$
D
24
Solution
$ a +6 d =3 $.......................(1)
$ Z = a ( a +3 d ) $
$ =(3-6 d )(3-3 d )$
$ =18 d ^2-27 d +9 $
Differentiating with respect to $ d $
$ \Rightarrow 36 d -27=0 $
$ \Rightarrow d =\frac{3}{4}, \text { from }(1) a =\frac{-3}{2},( Z =\text { minimum }) $
Now, $ S _{ a }=\frac{ n }{2}\left(-3+( n -1) \frac{3}{4}\right)=0 $
$\Rightarrow n =5 $
Now,
$ n !-4 a _{ n ( n +2)}=120-4\left( a _{35}\right) $
$ =120-4( a +(35-1) d )$
$ =120-4\left(\frac{-3}{2}+34 \cdot\left(\frac{3}{4}\right)\right) $
$ =120-4\left(\frac{-6+102}{4}\right) $
$ =120-96=24$
A
is equal to $\frac{27}{2}$
B
is equal to 9
C
does not exist
D
is equal to 27
Solution
$\displaystyle\lim _{x \rightarrow \infty} \frac{(\sqrt{3 x+1}+\sqrt{3 x-1})^6+(\sqrt{3 x+1}-\sqrt{3 x-1})^6}{\left(x+\sqrt{x^2-1}\right)^6+\left(x-\sqrt{x^2-1}\right)^6} x^3$
$\displaystyle\lim _{x \rightarrow \infty} x^3 \times\left\{\frac{x^3\left\{\left(\sqrt{3+\frac{1}{x}}+\sqrt{3-\frac{1}{x}}\right)^6+\left(\sqrt{3+\frac{1}{x}}-\sqrt{3-\frac{1}{x}}\right)^6\right\}}{x^6\left\{\left(1+\sqrt{1-\frac{1}{x^2}}\right)^6+\left(1-\sqrt{1-\frac{1}{x^2}}\right)^6\right\}}\right\}$
$=\frac{(2 \sqrt{3})^6+0}{2^6+0}=3^3=(27)$
A
3
B
$\frac{5}{2}$
C
2
D
$\frac{3}{2}$
Solution
$ 2 ae =|(1+\sqrt{2})-(1+\sqrt{2})|=2 \sqrt{2} $
$ ae =\sqrt{2} $
$ a =1 $
$ \Rightarrow b =1 $
$\because e =\sqrt{2}$
$ \Rightarrow$ Hyperbola is rectangular
$ \Rightarrow L \cdot R =\frac{2 b ^2}{ a }=2$
A
1
B
2
C
4
D
3
Solution
$(( p \wedge q ) \Rightarrow( r \vee q )) \wedge(( p \wedge r ) \Rightarrow q )$
We know, $p \Rightarrow q$ is equivalent to
$ \sim p \vee q$
$ (\sim( p \wedge q ) \vee( r \vee q )) \wedge(\sim( p \wedge r )) \vee q )) $
$ \Rightarrow(\sim p \vee \sim q \vee r \vee q ) \wedge(\sim p \vee \sim r \vee q )$
$ \Rightarrow(\sim p \vee r \vee t ) \wedge(\sim p \vee \sim r \vee q ) $
$ \Rightarrow( t ) \wedge(\sim p \vee \sim r \vee q )$
For this to be tautology, $(\sim p \vee \sim r \vee q )$ must be always true which follows for $r =\sim p$ or $r = q$.
A
$S$ is transitive but $T$ is not
B
both $S$ and $T$ are symmetric
C
neither $S$ nor $T$ is transitive
D
$T$ is symmetric but $S$ is not
Solution
For relation $T = a ^2- b ^2=- I$
Then, (b, a) on relation $R$
$ \Rightarrow b ^2- a ^2=- I $
$ \therefore T \text { is symmetric }$
$ S =\left\{( a , b ): a , b \in R -\{0\}, 2+\frac{ a }{ b }>0\right\} $
$2+\frac{ a }{ b }>0 \Rightarrow \frac{ a }{ b }>-2, \Rightarrow \frac{ b }{ a }<\frac{-1}{2}$
If $(b, a) \in S$ then
$2+\frac{b}{a}$ not necessarily positive
$\therefore S$ is not symmetric
A
$\frac{3}{2}$
B
$\frac{1}{4}$
C
$\frac{5}{4}$
D
$\frac{3}{4}$
Solution
$f(x)=\left|x^2-x+1\right|+\left[x^2-x+1\right] ; x \in[-1,2]$
Let $g( x )= x ^2- x +1$
$=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}$
$\because\left| x ^2- x +1\right| \text { and }\left[ x ^2- x +2\right]$
Both have minimum value at $x=1 / 2$
$ \Rightarrow $ Minimum $ f ( x )=\frac{3}{4}+0$
$=\frac{3}{4}$
A
$\frac{\pi}{8}$
B
$\frac{\pi}{48}$
C
$\frac{\pi}{16}$
D
$\frac{\pi}{12}$
Solution
$ \sin ^{-1} \sin \theta-\left(\frac{\pi}{2}-\sin ^{-1} \sin \theta\right)>0 $
$ \Rightarrow \sin ^{-1} \sin \theta>\frac{\pi}{4}$
$ \Rightarrow \sin \theta>\frac{1}{\sqrt{2}} $
$ \text { So, } \theta \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right) $
$ \theta \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right)=(a, b) $
$ \Rightarrow b-a=\frac{\pi}{2}=\alpha-\beta $
$ \Rightarrow \beta=\alpha-\frac{\pi}{2}$
$ \Rightarrow \alpha x^2+\beta x+\sin ^{-1}\left[(x-3)^2+1\right]+\cos ^{-1}\left[(x-3)^2+1\right]=0 $
$ x=3,9 \alpha+3 \beta+\frac{\pi}{2}+0=0$
$ \Rightarrow 9 \alpha+3\left(\alpha-\frac{\pi}{2}\right)+\frac{\pi}{2}=0 $
$ \Rightarrow 12 \alpha-\pi=0 $
$ \alpha=\frac{\pi}{12}$
A
500
B
450
C
650
D
900
Solution

$ \sigma_1^2=\frac{\sum x _{ i }^2}{100}-40^2 $
$ \sigma_2^2=\frac{\sum x _{ j }^2}{100}-55^2 $
$ 350=\sigma^2=\frac{\sum x _{ i }^2+\sum x _{ j }^2}{300}-(\overline{ x })^2$
$350=\frac{\left(1600+\alpha^2\right) \times 100+\left[(30-\alpha)^2+3025\right] \times 200}{300}-(50)^2$
$ 2850 \times 3=\alpha^2+2(30-\alpha)^2+1600+6050 $
$ 8550=\alpha^2+2(30-\alpha)^2+7650 $
$ \alpha^2+2(30-\alpha)^2=900 $
$ \alpha^2-40 \alpha+300=0 $
$ \alpha=10,30 $
$ \sigma_1^2+\sigma_2^2=10^2+20^2=500$
A
$\left(-\infty,-\frac{21}{4}\right] \cup\left[\frac{21}{4}, \infty\right)$
B
$\left(-\infty,-\frac{21}{4}\right] \cup[0, \infty)$
C
$\left(-\infty,-\frac{21}{4}\right) \cup(0, \infty)$
D
$\left(-\infty,-\frac{21}{4}\right] \cup[1, \infty)$
Solution
Sol. Let $y=\frac{x^2+2 x+1}{x^2-8 x+12}$
By cross multiplying
$y x^2-8 x y+12 y-x^2-2 x-1=0 $
$x^2(y-1)-x(8 y+2)+(12 y-1)=0$
Case $1, y \neq 1$
$ D \geq 0$
$ \Rightarrow(8 y+2)^2-4(y-1)(12 y-1) \geq 0$
$ \Rightarrow y(4 y+21) \geq 0 $

$ y \in\left(-\infty, \frac{-21}{4}\right] \cup[0, \infty)-\{1\}$
Case $2, y =1$
$ x^2+2 x+1=x^2-8 x+12 $
$ 10 x=11$
$x =\frac{11}{10} $ So, $y$ can be 1
Hence $y \in\left(-\infty, \frac{-21}{4}\right] \cup[0, \infty)$
A
four solutions two of which are negative
B
two solutions and both are negative
C
no solution
D
two solutions and only one of them is negative
Solution
$e ^{4 x }+8 e ^{3 x }+13 e ^{2 x }-8 e ^{ x }+1=0$
Let $e ^{ x }= t$
Now, $t ^4+8 t ^3+13 t ^2-8 t +1=0$
Dividing equation by $t ^2$,
$ t ^2+8 t +13-\frac{8}{ t }+\frac{1}{ t ^2}=0 $
$ t ^2+\frac{1}{ t ^2}+8\left( t -\frac{1}{ t }\right)+13=0 $
$ \left( t -\frac{1}{ t }\right)^2+2+8\left( t -\frac{1}{ t }\right)+13=0$
Let $t -\frac{1}{ t }= z$
$ z^2+8 z+15=0 $
$ (z+3)(z+5)=0$
$z=-3$ or $z=-5$
So, $t-\frac{1}{t}=-3$ or $t-\frac{1}{t}=-5$
$t^2+3 t-1=0$ or $t^2+5 t-1=0$
$t=\frac{-3 \pm \sqrt{13}}{2}$ or $t =\frac{-5 \pm \sqrt{29}}{2}$
as $t=e^x$ so $t$ must be positive,
$t =\frac{\sqrt{13}-3}{2}$ or $\frac{\sqrt{29}-5}{2}$
So, $x=\ln \left(\frac{\sqrt{13}-3}{2}\right)$ or $x=\ln \left(\frac{\sqrt{29}-5}{2}\right)$
Hence two solution and both are negative.
A
$\sqrt{2} i\left(\cos \frac{5 \pi}{12}-i \sin \frac{5 \pi}{12}\right)$
B
$\cos \frac{\pi}{12}-i \sin \frac{\pi}{12}$
C
$\sqrt{2}\left(\cos \frac{\pi}{12}+i \sin \frac{\pi}{12}\right)$
D
$\sqrt{2}\left(\cos \frac{5 \pi}{12}+i \sin \frac{5 \pi}{12}\right)$
Solution
$Z =\frac{ i -1}{\cos \frac{\pi}{3}+ i \sin \frac{\pi}{3}}=\frac{ i -1}{\frac{1}{2}+\frac{\sqrt{3}}{2} i }$
$=\frac{ i -1}{\frac{1}{2}+\frac{\sqrt{3}}{2} i } \times \frac{\frac{1}{2}-\sqrt{\frac{3}{2} i }}{\frac{1}{2}-\sqrt{3 / 2} i }=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{3}+1}{2} i$
Apply polar form,
$ r \cos \theta=\frac{\sqrt{3}-1}{2} $
$ r \sin \theta=\frac{\sqrt{3}+1}{2}$
Now, $\tan \theta=\frac{\sqrt{3}+1}{\sqrt{3}-1}$
So, $\theta=\frac{5 \pi}{12}$
A
$\frac{5}{4}$
B
$-1$
C
11
D
$\frac{11}{5}$
Solution
$ 2 \alpha+4 \beta+3 \gamma=5 $.........(1)
$ 2 \alpha+9 \beta+8 \gamma=0 $.........(2)
$10 \alpha+3 \beta+4 \gamma=0 $.........(3)
$ 8 \alpha+8 \beta+8 \gamma=0$.........(4)
Subtract (4) from (2)
$ -6 \alpha+\beta=0$
$ \beta=6 \alpha$.........(5)
From equation (4)
$ 8 \alpha+48 \alpha+8 \gamma=0 $
$ \gamma=-7 \alpha$.........(6)
From equation (1)
$ 2 \alpha+24 \alpha-21 \alpha=5$
$ 5 \alpha=5$
$ \alpha=1$
$ \beta=+6, \,\,\,\,\gamma=-7 $
$ \therefore 6 \alpha+9 \beta+7 \gamma $
$ =6+54-49$
$=11$
A
6
B
4
C
5
D
7
Solution
Equation of Plane :
$2( x -1)-3( y +1)-6( z +5)=0$
Or $2 x-3 y-6 z=35$
$\Rightarrow$ Required distance $=$
$\frac{|2(3)-3(-2)-6(2)-35|}{\sqrt{4+9+36}}$
$=5$
A
560
B
339
C
449
D
336
Solution
$\vec{ a }=\hat{ i }+2 \hat{ j }+3 \hat{ k }$
$\vec{ b }=\hat{ i }-\hat{ j }+2 \hat{ k }$
$ \vec{ c }=\hat{5 i }-3 \hat{ j }+3 \hat{ k }$
$ (\vec{ r }-\vec{ c }) \times \vec{ b }=0, \vec{ r } \cdot \vec{ a }=0$
$ \Rightarrow \vec{ r }-\vec{ c }=\lambda \vec{ b } $
$ \text { Also, }(\vec{ c }+\lambda \vec{ b }) \cdot \vec{ a }=0 $
$ \Rightarrow \vec{ a } \cdot \vec{ c }+\lambda(\vec{ a } \cdot \vec{ b })=0 $
$\therefore \lambda=\frac{\vec{ a } \cdot \vec{c}}{\vec{ a } \cdot \vec{b}}=\frac{-8}{5}$
$ \vec{ r }=\frac{5(5 \hat{ i }-3 \hat{ i }+3 \hat{ k })-8(\hat{ i }-\hat{ j }+2 \hat{ k })}{5}$
$ \vec{ r }=\frac{17 \hat{ i }-7 \hat{ j }+\hat{ k }}{5} $
$ |\vec{ r }|^2=\frac{1}{25}(289+50) $
$ 25|\vec{ r }|^2=339$
A
$\sqrt{\frac{2}{7}}$
B
$\frac{6}{\sqrt{14}}$
C
$\sqrt{\frac{7}{2}}$
D
$\sqrt{14}$
Solution
P: $8 x+\alpha_1 y+\alpha_2 z+12=0$
$L : \frac{ x +2}{2}=\frac{ y -3}{3}=\frac{ z +4}{5}$
$\because P$ is parallel to $L$
$ \Rightarrow 8(2)+\alpha_1(3)+5\left(\alpha_2\right)=0 $
$ \Rightarrow 3 \alpha_1+5\left(\alpha_2\right)=-16$
Also $y$-intercept of plane $P$ is 1
$\Rightarrow \alpha_1=-12$
And $\alpha_2=4$
$\Rightarrow$ Equation of plane $P$ is $2 x -3 y + z +3=0$
$\Rightarrow$ Distance of line $L$ from Plane $P$ is
$ =\left|\frac{0-3(6)+1+3}{\sqrt{4+9+1}}\right|$
$ =\sqrt{14}$
Answer: 196
Solution
As given $a + b + c + d =3$ or 5 or 7 or 11
if $\operatorname{sum}=3$
$ \left(1+x+x^2+\ldots . .+x^4\right)^4 \rightarrow x^3 $
$ \left(1-x^5\right)^4(1-x)^{-4} \rightarrow x^3 $
$ \therefore{ }^{4+3-1} C_3={ }^6 C_3=20$
If $\operatorname{sum}=5$
$ \left(1-4 x ^5\right)(1- x )^{-4} \rightarrow x ^5 $
$\Rightarrow{ }^{4+5-1} C _5-4 x ^{4.4+0-1} C _0={ }^8 C _5-4=52$
If sum $=7$
$ \left(1-4 x ^5\right)(1- x )^{-4} \rightarrow x ^7 $
$ \Rightarrow{ }^{4+5-1} C _4-{ }^{4.4+0-1} C _0={ }^8 C _5-4=52 $
$ \text { If sum }=11 $
$ \qquad \left(1-4 x ^5+6 x ^{10}\right)(1- x )^{-4} \rightarrow x ^{11} $
$ \Rightarrow{ }^{4+11-1} C _{11}-4 \cdot{ }^{4+6-4} C _6+6 \cdot{ }^{4+1-1} C _1 $
$ ={ }^{14} C _{11}-4 \cdot{ }^9 C _6+6.4=364-336+24=52 $
$ \therefore \text { Total matrices }=20+52+80+52=204$
Answer: 3
Solution
$2(\vec{ a } \times \vec{ b })=3(\vec{ c } \times \vec{ a })$
$ \vec{ a } \times(2 \vec{ b }+3 \vec{ c })=0$
$ \vec{ a }=\lambda(2 \vec{ b }+3 \vec{ c })$
$ |\vec{ a }|^2=\lambda^2|2 \vec{ b }+3 \vec{ c }|^2 $
$ |\vec{ a }|^2=\lambda^2\left(4|\vec{ b }|^2+9|\vec{ c }|^2+12 \vec{ b } \cdot \vec{ c }\right) $
$ 31=31 \lambda^2 \Rightarrow \lambda=\pm 1$
$ \vec{ a }=\pm(2 \vec{ b }+3 \vec{ c })$
$ \frac{|\vec{ a } \times \vec{ c }|}{|\vec{ a } \cdot \vec{ b }|}=\frac{2|\vec{ b } \times \vec{ c }|}{2 \vec{ b } \cdot \vec{ b }+3 \vec{ c } \cdot \vec{ b }} $
$ |\vec{ b } \times \vec{ c }|^2=|\vec{ b }|^2|\vec{ c }|^2-(\vec{ b } \cdot \vec{ c })^2=\frac{3}{4} $
$ \frac{|\vec{ a } \times \vec{ c }|}{|\vec{ a } \cdot \vec{ b }|}=\frac{2 \times \frac{\sqrt{3}}{2}}{2 \cdot \frac{1}{4}-\frac{3}{2}}=-\sqrt{3} $
$ \left(\frac{\vec{ a } \times \vec{ c }}{\vec{ a } \cdot \vec{ b }}\right)^2=3 $
Answer: 5040
Solution
$\left(\frac{4 x}{5}+\frac{5}{2 x^2}\right)^9$
Now, $T _{ r +1}={ }^9 C _{ r } \cdot\left(\frac{4 x }{5}\right)^{9- r }\left(\frac{5}{2 x ^2}\right)^{ r }$
$={ }^9 C _{ r } \cdot\left(\frac{4}{5}\right)^{9- r }\left(\frac{5}{2}\right)^{ r } \cdot x ^{9-3 r }$
Coefficient of $x^{-6}$ i.e. $9-3 r=-6 \Rightarrow r=5$
So, Coefficient of $x ^{-6}={ }^9 C _5\left(\frac{4}{5}\right)^4 \cdot\left(\frac{5}{2}\right)^5=5040$
Answer: 10
Solution
$ |x-y|< a \Rightarrow-a< x-y< a $
$ \Rightarrow x-y< a \text { and } x-y >-a$

$ P ( A )=\frac{\operatorname{ar}( OACDEG )}{( OBDF )} $
$ =\frac{\operatorname{ar}( OBDF )-\operatorname{ar}( ABC )-\operatorname{ar}( EFG )}{\operatorname{ar}( OBDF )} $
$ \Rightarrow \frac{11}{36}=\frac{(60)^2-\frac{1}{2}(60- a )^2-\frac{1}{2}(60- a )^2}{3600} $
$ \Rightarrow 1100=3600-(60- a )^2 $
$ \Rightarrow (60- a )^2=2500 \Rightarrow 60- a =50 $
$ \Rightarrow a =10$
Answer: 98
Solution
In, $\left(\frac{x^{\frac{5}{2}}}{2}-\frac{4}{x^{\ell}}\right)^9$
$ T _{ r +1}={ }^9 C _{ r } \frac{\left( x ^{5 / 2}\right)^{9- r }}{2^{9- r }}\left(\frac{-4}{ x ^{\ell}}\right)^{ r } $
$ =(-1)^{ r } \frac{{ }^9 C _{ r }}{2^{9- r }} 4^{ r } x ^{\frac{45}{2}-\frac{5 r }{2}- r } $
$=45-5 r -2 lr =0 $
$ r =\frac{45}{5+21}$ ....(1)
Now, according to the question, $(-1)^{ r } \frac{{ }^9 C _{ r }}{2^{9- r }} 4^{ r }=-84$
$=(-1)^{ r }{ }^9 C _{ r } 2^{3 r -9}=21 \times 4$
Only natural value of $r$ possible if $3 r-9=0$
$r =3$ and ${ }^9 C _3=84$
$\therefore 1=5$ from equation (1)
Now, coefficient of $x^{-31}=x^{\frac{45}{2}-\frac{5 r}{2}-\operatorname{lr}}$ at $1=5$, gives
$ r =5$
$ \therefore{ }^9 c _5(-1) \frac{4^5}{2^4}=2^\alpha \times \beta$
$ =-63 \times 2^7 $
$\Rightarrow \alpha=7, \beta=-63$
$ \therefore \text { value of }|\alpha \ell-\beta|=98$
Answer: 125
Solution
$y \geq|2 x -1|, \,\,\,\, y \leq\left| x ^2- x \right|$

Both curve are symmetric about $x=\frac{1}{2}$ Hence
$A=2 \int\limits_{\frac{3-\sqrt{5}}{2}}^{\frac{1}{2}}\left(\left(x-x^2\right)-(1-2 x)\right) d x$
$A=2 \int\limits_{\frac{3-\sqrt{5}}{2}}^{\frac{1}{2}}\left(-x^2+3 x-1\right) d x=2\left(\frac{-x^3}{3}+\frac{3}{2} x^2-x\right)_{\frac{3-\sqrt{5}}{2}}^{\frac{1}{2}}$
On solving $6 A +11=5 \sqrt{5}$
$(6 A +11)^2=125$
Answer: 5
Solution
$ \left|\text{Adj}\left(2 \text{Adj}\left(2 A ^{-1}\right)\right)\right| $
$ =\left|2 \text{Adj}\left(\text{Adj}\left(2 A ^{-1}\right)\right)\right|^{ n -1} $
$ =2^{ n ( n -1)}\left|\text{Adj}\left(2 A ^{-1}\right)\right|^{ n -1} $
$ =2^{ n ( n -1)}\left|\left(2 A ^{-1}\right)\right|^{( n -1)( n -1)} $
$ =2^{ n ( n -1)} 2^{ n ( n -1)( n -1)}\left| A ^{-1}\right|^{( n -1)( n -1)} $
$=2^{ n ( n -1)+ n ( n -1)( n -1)} \frac{1}{| A |^{( n -1)^2}} $
$ =\frac{2^{ n ( n -1)+ n ( n -1)( n -1)}}{2^{( n -1)^2}} $
$ =2^{ n ( n -1)+ n ( n +1)^2-( n -1)^2} $
$ =2^{( n -1)\left( n ^2- n +1\right)} $
$ \text { Now } 2^{( n -1)\left( n ^2- n +1\right)} $
$ 2^{( n -1)\left( n ^2- n +1\right)}=2^{84} $
$ \text { So, } n =5$
Answer: 6952
Solution
Separating odd placed and even placed terms we get
$ S =\left(1.1^2+3.5^2+\ldots .15 .(29)^2\right)-\left(2.3^2+4.7^2\right. +\ldots .+14 .(27)^2$
$ S =\displaystyle\sum_{ n =1}^8(2 n -1)(4 n -3)^2-\displaystyle\sum_{ n =1}^7(2 n )(4 n -1)^2$
Applying summation formula we get
$=29856-22904=6952$
Answer: 45
Solution
$ \frac{(2 n +1) !( n -1) !}{( n +2) !(2 n -1) !}=\frac{11}{21} $
$ \Rightarrow \frac{(2 n +1)(2 n )}{( n +2)( n +1) n }=\frac{11}{21} $
$ \Rightarrow \frac{2 n +1}{( n +1)( n +2)}=\frac{11}{42} $
$ \Rightarrow n =5 $
$ \Rightarrow n ^2+ n +15$
$=25+5+15=45$
Answer: 146










