JEE Main Physics Question Paper with Solution 2023 January 25th Shift 1 - Morning
A
$12\, \mu m$
B
$60\, \mu m$
C
$36\, \mu m$
D
$48 \,\mu m$
Solution
Given
$ D =1 m $
$\lambda=600 \times 10^{-9} m $
$n =5 $
As $ y _{ nth }=\frac{ n \lambda D }{ d } $
$\Rightarrow \frac{5 \times 600 \times 10^{-9} \times 1}{ d }=5 \times 10^{-2} $
$\Rightarrow d =\frac{5 \times 600 \times 10^{-9} \times 1}{5 \times 10^{-2}}=60 \times 10^{-6} m$
$\Rightarrow d =60\, \mu m$
A
$\frac{\pi}{6}$
B
$\frac{\pi}{2}$
C
$\frac{\pi}{4}$
D
$\frac{\pi}{3}$
Solution

$ T \sin \theta=\frac{ mv^2}{ R } $
$ \tan \theta=\frac{ v ^2}{ Rg }$
$ \tan \theta=\frac{20^2}{40 \times 10}$
$ \tan \theta=1$
$\Rightarrow \theta=\frac{\pi}{4}$
A
Positive direction of $z$
B
Negative direction of $y$
C
Positive direction of $x$
D
Negative direction of $x$
Solution
As, poynting vector
$\vec{ S }=\vec{ E } \times \vec{ H }$
Given energy transport $=$ negative $z$ direction
Electric field $=$ positive y direction
$(-\hat{ k })=(+\hat{ j }) \times[\hat{ i }]$
Hence according to vector cross product magnetic field should be positive $x$ direction.
A
Inversely proportional to square root of temperature $\left(\sqrt{\frac{1}{T}}\right)$
B
Proportional to square root of temperature $(\sqrt{T})$
C
Proportional to square of temperature $\left(T^2\right)$
D
Proportional to temperature (T)
Solution
The rms speed of a gas molecule is
$V _{ RMS }=\sqrt{\frac{3 RT }{ M }}$
$V _{ RMS } \propto \sqrt{ T }$
A
$\frac{\lambda_0}{2}$
B
$3 \lambda_0$
C
$\frac{\lambda_0}{\sqrt{2}}$
D
$9 \lambda_0$
Solution
When electron is accelerated through potential difference $V$, then
K.E. $= eV $
$ \Rightarrow \lambda=\frac{ h }{\sqrt{2 m ( KE )}}=\frac{ h }{\sqrt{2 meV }} $
$ \therefore \lambda \alpha \frac{1}{\sqrt{ V }} $
$ \therefore \frac{\lambda}{\lambda_0}=\sqrt{\frac{20}{40}} $
$ \therefore \lambda=\frac{\lambda_0}{\sqrt{2}}$
A
A is true but $R$ is false
B
A is false but $R$ is true
C
Both $A$ and $R$ are true but $R$ is NOT the correct explanation $A$
D
Both $A$ and $R$ are true and $R$ is correct explanation $A$
Solution
Theory based
Photodiodes are operated in reverse bias condition.
For $P - N$ junction current in forward bias (for $V \geq V _0$ ) is always greater than current in reverse bias $\left(\right.$ for $V \leq V _{ Z }$ ) .
Hence Assertion if false but Reason is true
A
$4: 1$
B
$1: 1$
C
$8: 1$
D
$2: 1$
Solution
Nuclear density is independent of mass number As nuclear density $=\frac{ Au }{\frac{4}{3} \pi R ^3}$
Also, $R = R _0 A ^{\frac{1}{3}}$
And $R ^3= R _0^3 A$
$\Rightarrow$ Nuclear density $=\frac{ Au }{\frac{4}{3} \pi R _0^3 A }$
Nuclear density $=\frac{3 u }{4 \pi R _0^3}$
$\Rightarrow$ Nuclear density is independent of $A$
A
$240\, N$
B
$30\, N$
C
$300\, N$
D
$90\, N$
Solution

Taking torque about point $C$
$ \frac{ T }{2} \times 60=20 \times 50+80 \times 100$
$ \Rightarrow 3 T =100+800 $
$ \Rightarrow=300\, N$
A
$l=10\, m$
B
$l=100\, m$
C
$l=5\, m$
D
$l=6.8 \, m$
Solution
$ I =2 A $
$ \Delta V =3.4 V$
Using Ohm's Law $ R =\frac{3.4}{2}=1.7 \Omega$
$1.7=\frac{\rho L }{ A } $
$ L =\frac{1.7( A )}{\rho} $
$ M =$ ( density volume )
Volume $=\frac{8.92 \times 10^{-3}}{8.92 \times 10^3}=10^{-6} $
$ L ^2=\frac{1.7}{\rho}\left(10^{-6}\right)=\frac{1.7}{1.7} \times 10^2 $
$ L =10\, m$
A
$10 \,kHz$
B
$2.5 \,kHz$
C
$20\, kHz$
D
$5\, kHz$
Solution
Given
Signal frequency $f _{ m }=5 \,kHz$
Carrier wave frequency $f_c=2 \,MHz$
$f _{ c }=2000\, KHz$
The resultant signal will have band width of frequency given by
$ {\left[\left( f _{ c }+ f _{ m }\right)-\left( f _{ c }- f _{ m }\right)\right]} $
$\Rightarrow[(2000+5)-(2000-5)] kHz$
$ \Rightarrow 10\, kHz$
A
$\frac{1}{4}$
B
4
C
$\frac{1}{2}$
D
2
Solution
At surface of earth time period
$T=2 \pi \sqrt{\frac{\ell}{ g }}$
At height $h = R$
$ g ^{\prime}=\frac{ g }{\left(1+\frac{ h }{ R }\right)^2}=\frac{ g }{4} $
$\therefore xT =2 \pi \sqrt{\frac{\ell}{( g / 4)}} $
$\Rightarrow xT =2 \times 2 \pi \sqrt{\frac{\ell}{ g }}$
$ \Rightarrow xT =2 T \Rightarrow x =2$
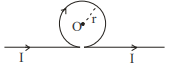
A
A-III, B-IV, C-I, D-II
B
A-I, B-III, C-IV, D-II
C
A-III, B-I, C-IV, D-II
D
A-II, B-I, C-IV, D-III
Solution
(A) 
$B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi) $ (in the plane)
$ B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
Hence magnetic field at $O$ is
$B _0=-\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi)-\frac{\mu_0}{4 \pi} \frac{ I }{ r } $
$B _0=\frac{\mu_0}{2 \pi} \frac{ I }{ r }(\pi-1) \ldots \ldots . . \text { (III) }$

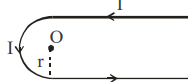
$ B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) $ (out of the plane)
$ B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
Hence magnetic field at $O$ is
$ B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi)+\frac{\mu_0}{4 \pi} \frac{ I }{ r }$
$ B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi+2) \ldots \text { (I) }$

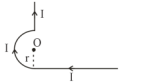
$B _{ ab }=\frac{\mu_0}{4 \pi} \frac{I}{ r } $ (in the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) $ (in the plane)
$ B _{ de }=0 $ (at the axis)
Hence magnetic field at $O$ is
$B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(1+\pi) \ldots \text { (IV) }$

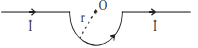
$B _{ ab }=0$ (at the axis)
$B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi)$ (out of the plane)
$B _{ de }=0$ (at the axis)
Hence magnetic field at $O$ is
$B _0=\frac{\mu_0 I }{4 r } \ldots$
A
$900 K$
B
$300 K$
C
$1000 K$
D
$360 K$
Solution

But $\eta=1-\frac{ T _2}{ T _1} $
$ \therefore \frac{1}{2}=1-\frac{ T _2}{600} $
$\Rightarrow \frac{ T _2}{600}=\frac{1}{2} \Rightarrow T _2=300\, K$
Now efficiency is increased to $70 \%$ and $T _2=300$
$K$, Let temp of source $T _1= T$
$\Rightarrow \frac{7}{10}=1-\frac{300}{ T }$
$\Rightarrow \frac{300}{ T }=1-\frac{7}{10}$
$ \Rightarrow \frac{300}{ T }=\frac{3}{10} $
$ \therefore T =1000 \,K$
A
$\frac{10}{3} \varepsilon_0 F$
B
$\frac{3}{10} \varepsilon_0 F$
C
$24 \varepsilon_0 F$
D
$10 \varepsilon_0 F$
Solution

This can be seen as two capacitors in series combination so
$ \frac{1}{ C _{ eq }}=\frac{1}{ C _1}+\frac{1}{ C _2} $
$=\frac{1}{\frac{ K \in_0 A }{ t }}+\frac{1}{\frac{\in_0 A }{ d - t }}$
$ =\frac{ t }{ K \in_0 A }+\frac{ d - t }{\epsilon_0 A } $
$ =\frac{1 \times 10^{-3}}{5 \epsilon_0 \times 40 \times 10^{-4}}+\frac{1 \times 10^{-3}}{\epsilon_0 40 \times 10^{-4}} $
$ \frac{1}{ C _{ eq }}=\frac{1}{20 \epsilon_0}+\frac{1}{4 \epsilon_0} $
$ C _{ eq }=\frac{20 \times 4 \epsilon_0}{24}=\frac{10 \epsilon_0}{3} F $
A
2 minutes
B
1 minute
C
$1.4$ minutes
D
$0.5$ minute
Solution
$ \frac{\Delta Q }{\Delta t }=- K \left( T - T _0\right)$
$ \frac{\Delta Q }{\Delta t }=- K \left( T _{ avg }- T _0\right)$
(i) $\frac{ ms \times 12}{2}=- K \left(\frac{98+86}{2}-22\right)$
$ 6=-\frac{ K }{ ms }\left[\frac{98+86}{2}-22\right] $
$ 6=-\frac{ K }{ ms }[70] \ldots . \ldots . . \text { (i) }$
(ii) $\frac{ ms \times 6}{\Delta t }=- K \left(\frac{75+69}{2}-22\right)$
$\frac{6}{\Delta t }=-\frac{ K }{ ms }(50) .....$(ii)
(ii) $\div$ (i)
$ \frac{6}{\Delta t (6)}=\frac{50}{70} $
$ \Delta t =\frac{7}{5}=1.4 \min$
A
A-III , B-IV , C-I , D-II
B
A-IV, B-III, C-II, D-I
C
A-IV , B-III , C-I , D-II
D
A-II , B-I , C-III , D-IV
Solution
(A) Surface Tension $=\frac{ F }{\ell} =\frac{ MLT ^{-2}}{ L }= MI ^{-1} T ^{-2} $
$ = Kgs ^{-2}( IV )$
(B) Pressure $=\frac{ F }{ A }=\frac{ MLT ^{-2}}{ L ^2} $
$ = kg m ^{-1} s ^{-2} \text { (III) }$
(C) Viscosity $ =\frac{ F }{ A \left(\frac{ dV }{ dz }\right)}=\frac{ MLT ^{-2}}{ L ^2\left(\frac{ LT ^{-1}}{ L }\right)}$
$= MI ^{-1} T ^{-1}= kg \,m ^{-1} s ^{-1}( I )$
(D) Impulse $ =\int Fdt = MLT ^{-2} \times T$
$ = MLT ^{-1}= Kg \,ms ^{-1} \text { (II) }$
So A-(IV), B-(III), C-(I), D- (II)
A
1 hour 24 minutes
B
1 hour 40 minutes
C
12 hours
D
24 hours
Solution

Let at some time particle is at a distance $x$ from centre of Earth, then at that position field
$ E =\frac{ GM }{ R ^3 }x $
$ \therefore $ Acceleration of particle
$ \vec{ a }=-\frac{ GM }{ R ^3} \vec{ x }$
$ \Rightarrow \omega=\sqrt{\frac{ GM }{ R ^3}}=\sqrt{\frac{ g }{ R }}$
Now $T =\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{ R }{ g }}$
$ \Rightarrow T =2 \times 3.14 \times \sqrt{\frac{6400 \times 10^3}{10}} $
$ =2 \times 3.14 \times 800 \,\sec \approx 1 $ hour $ 24 $ minutes
A
$1 / 4$
B
4
C
16
D
1/16
Solution
The resonance frequency of LC oscillations circuit is
$ \omega_0=\frac{1}{\sqrt{ LC }} $
$ L \rightarrow 2 L$
$ C \rightarrow 8 C $
$ \omega=\frac{1}{\sqrt{2 L \times 8 C }}=\frac{1}{4 \sqrt{ LC }}$
$ \omega=\frac{\omega_0}{4}$
So $x=\frac{1}{4}$
A
$2.4 \times 10^3 A m ^{-1}$
B
$1.2 \times 10^3 A m ^{-1}$
C
$1 Am ^{-1}$
D
$2.4 \times 10^{-3} A m ^{-1}$
Solution
Magnetic field at centre inside the solenoid is given by
$B =\mu_0 nI$
So magnetic intensity at centre
$H =\frac{ B }{\mu_0}= nI =\left(\frac{1200}{2}\right)(2) $
$ H =1.2 \times 10^3 Am ^{-1}$
A
$\frac{v_1 v_2}{2\left(v_1+v_2\right)}$
B
$\frac{2 x}{v_1+v_2}$
C
$\frac{2 v_1 v_2}{v_1+v_2}$
D
$\frac{v_1+v_2}{2}$
Solution

Average velocity $=\frac{\text { Total displacement }}{\text { Total time }} $
$ =\frac{ x + x }{\frac{ x }{ v _1}+\frac{ x }{ v _2}}=\frac{2 v _1 v _2}{ v _1+ v _2}$
Answer: 45
Solution
$0.5 e =\frac{1}{2} mv _{ x }^2 \Rightarrow v _{ x }=\sqrt{\frac{ e }{ m }}$
Along $x L = v _{ x } t =\sqrt{\frac{ e }{ m } t }$
Along $y v _{ y }=\frac{ eE }{ m } t$
$\operatorname{dividing} \frac{ v _{ y }}{ L }= E \sqrt{\frac{ e }{ m }}= Ev _{ x }$
$\Rightarrow \operatorname{Tan} \theta=\frac{ v _{ y }}{ v _{ x }}= E \times L =10 \times 0.1=1$
$\theta=45^{\circ}$
Answer: 10
Solution

$ R _{ eq }=3+(2 \| 2)+6 $
$R _{ eq }=3+1+6 $
$ R _{ eq }=10 \Omega$
Answer: 4
Solution
$ \vec{ P } \times \vec{ Q }= \begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 3 & \sqrt{3} & 2 \\ 4 & \sqrt{3} & 2.5\end{vmatrix}=\sqrt{3} \frac{\hat{ i }}{2}+\frac{\hat{ j }}{2}-\sqrt{3} \hat{ k } $
$\Rightarrow \frac{\vec{ P } \times \vec{ Q }}{|\vec{ P } \times \vec{ Q }|}=\frac{1}{2}\left(\sqrt{3} \frac{\hat{ i }}{2}+\frac{\hat{ j }}{2}-\sqrt{3} \hat{ k }\right) $
$ =\frac{1}{4}(\sqrt{3} \hat{ i }+\hat{ j }-2 \sqrt{3} \hat{ k }) x =4$
Answer: 2
Solution

$ 2 \cos ( kx )=\frac{ mvd v}{ dx } $
$ \int\limits_0^{ v } vdv =2 \int\limits_0^{ x } \cos ( kx ) dx $
$ \frac{ m v^2}{2}=\frac{2}{ k } \sin kx $
$ K.E =\frac{2}{ k } \sin \theta $
$n = 2$
Answer: 100
Solution
$ f =\frac{1}{2 \pi \sqrt{ LC }} $
$ 2000\, Hz =\frac{1}{2 \pi \sqrt{ L \times 62.5 \times 10^{-9}}}$
$ L =\frac{1}{4 \pi^2 \times 2000^2 \times 62.5 \times 10^{-9}}=0.1 H =100\, mH $
Answer: 5
Solution

From graph :
$F =\Delta L $
$ Y =\frac{ FL }{ A \Delta L }$
$Y =\frac{ L }{ A } $
$ Y =\frac{62.8 \times 10^{-2}}{\pi\left(2 \times 10^{-3}\right)^2}$
$ Y =5 \times 10^4 N / m ^2$
Answer: 18
Solution
$\Delta \phi=\frac{2 \pi}{\lambda} \Delta x$
$ \frac{\pi}{3}=\frac{2 \pi}{\lambda}(6 m )$
$ \Rightarrow \lambda=36 \,m $
$ V = f \lambda=(500 \,Hz )(36\, m )$
$ =18000 \,m / s =18 \,km / s $
Answer: 52
Solution

$ \sin c =\frac{1}{\sqrt{2}}$
$ c =45^{\circ}$
$\sin c =\mu \sin \theta$
$\frac{1}{\sqrt{2}}=\sqrt{2} \sin \theta$
$ \theta=30^{\circ}$
Lateral displacement:
$ x=t \sin (i-r) \sec r$
$x=\sqrt{3} \sin \left(45^{\circ}-30^{\circ}\right) \sec 30^{\circ}$
$ x=\sqrt{3}(0.26)\left(\frac{2}{\sqrt{3}}\right) $
$ X=0.52\, cm $
$x=52 \times 10^{-2} cm$
Answer: 17
Solution
$I _{ cm }=\frac{ mR ^2}{2}$
$ I _{ AB }=\frac{ mR ^2}{2}+ m \left(\frac{2 R }{3}\right)^2=\frac{17}{18} mR ^2 $
$ \frac{ I _{ AB }}{ I _{ cm }}=\frac{17}{9} \Rightarrow x =17$
Answer: 27
Solution
________$n =4$
_________$ n =3 $
_________ $n =2 $
__________$ n =1$
Second excited state $\rightarrow$ first excited state
$ n =3 \rightarrow n =2$
$ \frac{ hc }{\lambda_0}=13.6\left(\frac{1}{2^2}-\frac{1}{3^2}\right).....$(i)
Third excited state $\rightarrow$ second orbit $n =4 \rightarrow n =2$
$\frac{ hc }{\left(20 \lambda_0 / x \right)}=13.6\left(\frac{1}{2^2}-\frac{1}{4^2}\right) ......$(ii)
(ii) $\div$ (i)
$ \frac{x}{20}=\frac{\frac{1}{2^2}-\frac{1}{4^2}}{\frac{1}{2^2}-\frac{1}{3^2}}$
$ x=27$
JEE Main Chemistry Question Paper with Solution 2023 January 25th Shift 1 - Morning
A
$He < Ne < Kr _{ r }< Xe _{ e }$
B
$He < Xe < Kr < Ne$
C
$He < Kr < Xe _{ e }< Ne$
D
$Xe < Kr < Ne < He$
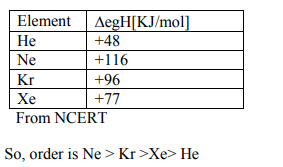
A
$\frac{16}{27} \pi$
B
$\frac{4}{9} x$
C
$\frac{9}{4} x$
D
$\frac{27}{16} x$
Solution
$Li ^{2+}$
$r_2= x = k \times \frac{2^2}{3}=\frac{4 k }{2}$
$ Be ^{3+}$
$ r _3= y = k \times \frac{3^2}{4}$
$ \frac{y}{x}=\frac{9}{4} \times \frac{3}{4}=\frac{27}{16} $
$ y=\frac{27}{16} x$
A
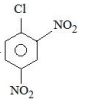
B
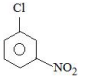
C
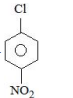
D
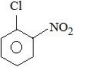
Solution
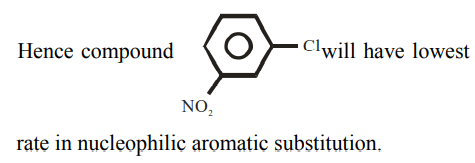
Electron withdrawing groups are highly ineffective at meta position in nucleophilic aromatic substitution reactions.
A
$P _4 O _6$ and $H _3 PO _3$
B
$PCl _5$ and $H _3 PO _4$
C
$PCl _3$ and $H _3 PO _3$
D
$POCl _3$ and $H _3 PO _4$
Solution
$P _4+8 SOCl _2 \rightarrow \underset{[A]}{4 PCl _3}+4 SO _2+2 S _2 Cl _2$
$PCl _3+3 H _2 O \rightarrow \underset{[B]}{H _3 PO _3}+3 HCl$

A
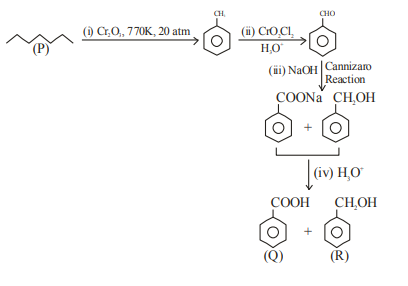
(i) $Cr _2 O _3, 770 K , 20 atm$; (ii) $CrO _2 Cl _2, H _3 O ^{+}$; (iii) $NaOH$; (iv) $H _3 O ^{+}$
B
(i) $Mo _2 O _3, \Delta$; (ii) $CrO _2 Cl _2, H _3 O ^{+}$; (iii) $NaOH$; (iv) $H _3 O ^{+}$
C
(i) $CrO _2 Cl _2, H _3 O ^{+}$; (ii) $Cr _2 O _3, 770 K , 20 atm$;(iii) $NaOH$; (iv) $H _3 O ^{+}$
D
(i) $KMnO _4, OH ^{-}$; (ii) $Mo _2 O _3, \Delta$; (iii) $NaOH$; (iv) $H _3 O ^{+}$
A
$A \rightarrow$ iv, $B \rightarrow$ ii, $C \rightarrow$ ii., $D \rightarrow i$
B
$A \rightarrow i , B \rightarrow iii , C \rightarrow$ ii, $D \rightarrow$ iv
C
$A \rightarrow$ iii, $B \rightarrow$ i, $C \rightarrow$ iv, $D \rightarrow$ ii
D
$A \rightarrow$ i. $B \rightarrow$ iii, $C \rightarrow$ iv, $D \rightarrow$ ii
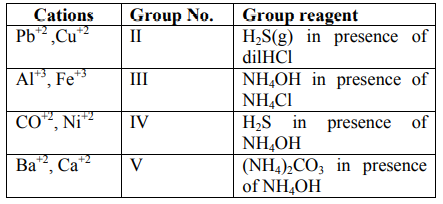
A
$CaCl _2, NH _4^{+},\left( NH _4\right)_2 CO _3$
B
$CaCl _2, NH _3, NH _4 HCO _3$
C
$Ca ( OH )_2, NH _3, NH _4 HCO _3$
D
$Ca ( OH )_2, NH _4^{+},\left( NH _4\right)_2 CO _3$
Solution
$\underset{\text { (A) }}{ Ca ( OH )_2}+2 NH _4 Cl \xrightarrow {\Delta} \underset{\text { (B) }}{2NH_3} + CaCl _2+2 H _2 O$
$\underset{\text { (B) }}{ NH _3}+ H _2 O +\underset{\text { (exc) }}{ CO _2} \longrightarrow \underset{\text { (C) }}{ NH _4 HCO _3}$
$\underset{(c)}{NH _4 HCO _3}+ NaCl \longrightarrow NaHCO _3 \downarrow+ NH _4 Cl$
A
$NH _3> Me _3 N > MeNH _2> Me _2 NH$
B
$Me _2 NH > Me _3 N > MeNH _2> NH _3$
C
$Me _2 NH > MeNH _2> Me _3 N > NH _3$
D
$Me _3 N > Me _2 NH > MeNH _2> NH _3$
Solution
In aqueous medium basic strength is dependent on electron density on nitrogen as well as solvation of cation formed after accepting $H ^{+}$. After considering all these factors overall basic strength order is
$Me _2 NH > MeNH _2> Me _3 N > NH _3$
A
A-II, B-IV, C-I, D-III
B
A-IV, B-III, C-II, D-I
C
A-II, B-I, C-III, D-IV
D
A-II, B-I, C-IV, D-III
A
Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$
B
A is false but $R$ is true
C
A is true but $R$ is false
D
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
Solution
For Assertion :Acetal and ketals are basically ethers hence they must be stable in basic medium but should break down in acidic medium.
Hence assertion is correct.
For reason: Alkoxide ion $\left( RO ^{-}\right)$is not considered a good leaving group hence reason must be false.
A
$CaO + SiO _2 \rightarrow CaSiO _3$
B
$2 Cu _2 S +3 O _2 \rightarrow 2 Cu _2 O +2 SO _2$
C
$FeO + SiO _2 \rightarrow FeSiO _3$
D
$2 FeS +3 O _2 \rightarrow 2 FeO +2 SO _2$
Solution
$ CuFeS _2+ O _2 \xrightarrow{\text { Partial roasting }}$
$Cu _2 S + FeO + SO _2+\underset{\text { very small }}{ FeS }+ \underset{\text{very small}}{Cu _2 O} $
$ Cu _2 S + O _2 \rightarrow Cu _2 O + SO _2$
$FeS + O _2 \rightarrow FeO + SO _2 $
$ FeO + SiO _2 \rightarrow FeSiO _3$
No formation of calcium silicate $\left( CaSiO _3\right)$ in extraction of $Cu$.
A
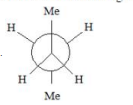
B
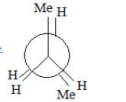
C
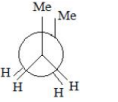
D
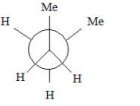
Solution

vanderwaal and torsional strain. Hence it must be
most stable.
A
$100 \,mL$ marketed solution contains $25\, g$ of $H _2 O _2$.
B
$1 L$ marketed solution contains $75 \,g$ of $H _2 O _2$.
C
$1 L$ marketed solution contains $250\, g$ of $H _2 O _2$.
D
$1 L$ marketed solution contains $25\, g$ of $H _2 O _2$.
Solution
Volume $=11.35 \times M$
Strength
$M =\frac{25}{11.35} M $
$ g / L =25 \times 34 / 11.35$
$ =74.889$
A
An antibiotic must be a product of metabolism.
B
An antibiotic should be effective in low concentrations.
C
An antibiotic is a synthetic substance produced as a structural analogue of naturally occurring antibiotic.
D
An antibiotic should promote the growth or survival of microorganisms.
Solution
An antibiotic should not promote growth or survival of microorganisms. Antibiotics should inhibit growth of microbes.
A
$A \rightarrow$ iii, $B \rightarrow$ iv, $C \rightarrow$ ii, $D \rightarrow$ i
B
$A \rightarrow iv , B \rightarrow$ iii, $C \rightarrow i , D \rightarrow$ ii
C
A $\rightarrow$ iii, $B \rightarrow iv , C \rightarrow i , D \rightarrow ii$
D
A $\rightarrow$ i, B $\rightarrow$ ii, $C \rightarrow$ iii, $D \rightarrow$ iv
Solution

Represents $\beta$-D- $(+)$ Glucopyranose

Represents $\beta$-D- $(-)$ Fructofuranose
(from the given options best answer is D)
A
$X =[ O ], Y = NO , A = O _2, B = O _3$
B
$X = N _2 O , Y =[ O ], A = O _3, B = NO$
C
$X =\frac{1}{2} O _2, Y = NO _2, A = O _3, B = O _2$
D
$X = NO , Y =[ O ], A = O _2, B = N _2 O _3$
A
$X _2 Y _{1.5}$
B
$X _{2.5} Y$
C
$XY _2, 5$
D
$X _{1.5} Y _2$
Solution
$ X_{4 x_8^1+1 \times 1}^1 Y_{6 \times \frac{1}{3} \times \frac{1}{2}}$
$ \Rightarrow X _{\frac{1}{2}+1} Y _1 $
$ \Rightarrow X _{\frac{2}{3}} Y _1 $
$ \Rightarrow X _{1.5} Y _1$
$ \Rightarrow X _3 Y _2 $
Answer: 9079
Solution
In resultant solution
$n _{ NH _3}= 0.1-0.02=0.08 $
$ n _{ NH _4 Cl }= n _{ NH _4^{+}}=0.1+0.02=0.12$
$pOH = pK _{ b }+\log \frac{\left[ NH _4^{+}\right]}{\left[ NH _3\right]}$
$=4.745+\log \frac{0.12}{0.08}$
$=4.745+\log \frac{3}{2}$
$=4.745+0.477-0.301 $
$ pOH =4.921 $
$ pH =14- pH$
$=9.079$
Answer: 41500
Solution
$ \pi= M ^{\prime} RT =\left(\frac{ W / M }{ V }\right) RT$
$ \Rightarrow \pi=\left(\frac{ W }{ V }\right)\left(\frac{1}{ M }\right) RT = C \left(\frac{ RT }{ M }\right) $
$ \Rightarrow \frac{\pi}{ C }=\frac{ RT }{ M } \neq f ( c )$
If we assume graph between $\frac{\pi}{C}$ and $C$

Assuming $\pi$ vs $C$ graph
Slope $=\frac{ RT }{ M }=\frac{0.083 \times 300}{ M }=6 \times 10^{-4}$
$ \therefore M =\frac{0.083 \times 300}{6 \times 10^{-4}}=\frac{830 \times 300}{6} $
$=41,500\, gm / mole$
Answer: 60
Solution
$t _{1 / 2}= T _{50}=30 \min$
$T _{75}=2 t _{1 / 2}=30 \times 2=60 \min$
Answer: 10
Solution
$ \frac{1}{2} H _2( g )+ Fe ^{3+}( aq .) \longrightarrow H ^{+}( aq )+ Fe ^{2+}( aq .) $
$ E = E ^{ o }-\frac{0.059}{1} \log \frac{\left[ Fe ^{2+}\right]}{\left[ Fe ^{3+}\right]} $
$ \Rightarrow 0.712=(0.771-0)-\frac{0.059}{1} \log \frac{\left[ Fe ^{2+}\right]}{\left[ Fe ^{3+}\right]}$
$ \Rightarrow \log \frac{\left[ Fe ^{2+}\right]}{\left[ Fe ^{3+}\right]}=\frac{(0.771-0712)}{0.059}=1$
$ \Rightarrow \frac{\left[ Fe ^{2+}\right]}{\left[ Fe ^{3+}\right]}=10$
Answer: 42
Solution
$\% \text { sulphur } =\frac{32}{233} \times \frac{\text { weight of } BaSO _4 \text { formed }}{\text { weight of organic compound }} \times 100$
$ =\frac{32}{233} \times \frac{1.4439}{0.471} \times 100$
$ =42.10$
Nearest integer 42
Answer: 12
Solution
millimole of $NaOH =0.24 \times 25$
$\therefore $ millimole of acid $=0.24 \times 25$
$ \Rightarrow $ mass of acid $=0.24 \times 25 \times 24.2\, mg$
for pure acid,
$V =\frac{ w }{ d } ;( d =1.21 kg / L =1.21 g / ml )$
$\therefore V = \frac{0.24 \times 25 \times 24.2}{1.12} \times 10^{-3} $
$ =120 \times 10^{-3} ml $
$ =12 \times 10^{-2} ml$
Answer: 6
Solution
(Total no, of lone pairs on oxygen atoms = 6
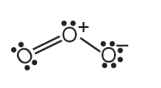
Answer: 360
Solution
$C _6 H _{12} O _6( s )+6 O _2 \rightarrow 6 CO _2( g )+6 H _2 O ( l )$
Extra energy used to convert $H _2 O ( l )$ into $H _2 O ( l )$ into $H _2 O ( g )$
$=\frac{1800}{2} =900 kJ$
$\Rightarrow 900= n _{ H _2 O } \times 45$
$n _{ H _2 O } =\frac{900}{45}=20 \text { mole } $
$W _{ H _2 O } =20 \times 18=360 g$
Answer: 4
Solution


$\left[ Cu \left( NH _3\right)_4\right]^{+2}: Cu ^{+2} \Rightarrow$ one unpaired electron : paramagnetic
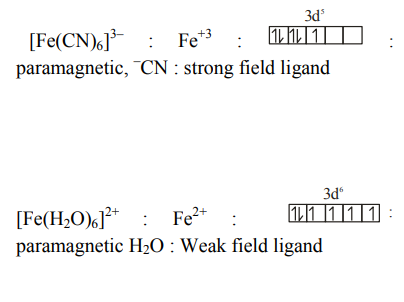
JEE Main Mathematics Question Paper with Solution 2023 January 25th Shift 1 - Morning
A
$3.92$
B
$3.96$
C
$4.04$
D
$4.08$
Solution
$\displaystyle \sum_{ i =1}^{ n } x _{ i }=10 n $
$ \displaystyle\sum_{ i =1}^{ n } x _{ i }-8+12=(10.2) n$
$ \therefore n =20$
Now $ \frac{\displaystyle\sum_{ i =1}^{20} x _{ i }^2}{20}-(10)^2=4 \Rightarrow \displaystyle\sum_{ i =1}^{20} x _{ i }^2=2080 $
$ \frac{\displaystyle\sum_{ i =1}^{20} x _{ i }^2-8^2+12^2}{20}-(10.2)^2 $
$ =108-104.04=3.96$
A
3025
B
1210
C
5445
D
4895
Solution
$ a _{ r }={ }^{10} C _{10- r }={ }^{10} C _{ r } $
$\Rightarrow \displaystyle\sum_{ r =1}^{10} r ^3\left(\frac{{ }^{10} C _{ r }}{{ }^{10} C _{ r -1}}\right)^2=\displaystyle\sum_{ r =1}^{10} r ^3\left(\frac{11- r }{ r }\right)^2=\displaystyle\sum_{ r =1}^{10} r (11- r )^2 $
$ =\displaystyle\sum_{ r =1}^{10}\left(121 r + r ^3-22 r ^2\right)=1210$
A
$\frac{x^2}{5-2 x^3\left(2+\log _e x^3\right)}$
B
$\frac{x^2}{3 x^3\left(1+\log _e x^2\right)-2}$
C
$\frac{x^2}{7-3 x^3\left(2+\log _e x^2\right)}$
D
$\frac{x^2}{2 x^3\left(2+\log _e x^3\right)-3}$
Solution
$ \frac{d y}{d x}-\frac{y}{x}=y^3\left(1+\log _e x\right) $
$ \frac{1}{y^3} \frac{d y}{d x}-\frac{1}{x y^2}=1+\log _e x $
$\text { Let }-\frac{1}{y^2}=t \Rightarrow \frac{2}{y^3} \frac{d y}{d x}=\frac{d t}{d x} $
$ \therefore \frac{d t}{d x}+\frac{2 t}{x}=2\left(1+\log _e x\right) $
$ \text { I.F. }=e^{\int \frac{2}{x} d x}=x^2 $
$\frac{-x^2}{y^2}=\frac{2}{3}\left(\left(1+\log _e x\right) x^3-\frac{x^3}{3}\right)+C $
$ y(1)=3 $
$ \frac{y^2}{9}=\frac{x^2}{5-2 x^3\left(2+\log _e x^3\right)} $
OR
$ x d y=y d x+x^3\left(1+\log _e x\right) d x$
$ \frac{x d y-y d x}{y^3}=x\left(1+\log _e x\right) d x$
$ -\frac{x}{y} d\left(\frac{x}{y}\right)=x^2\left(1+\log _e x\right) d x $
$ -\left(\frac{x}{y}\right)^2=2 \int x^2\left(1+\log _e x\right) d x$
A
$\log _{ e } 17-\log _{ e } 18$
B
$\log _e 19-\log _e 20$
C
$\frac{1}{2}\left(\log _e 19-\log _e 17\right)$
D
$\frac{1}{2}\left(\log _e 17-\log _e 19\right)$
Solution
Put $x^2=t$
$\int \frac{ dt }{( t +1)( t +3)}=\frac{1}{2} \int\left(\frac{1}{t+1}-\frac{1}{t+3}\right) d t$
$ f(x)=\frac{1}{2} \ln \left(\frac{x^2+1}{x^2+3}\right)+C $
$ f(3)=\frac{1}{2}(\ln 10-\ln 12)+C$
$ \Rightarrow C=0 $
$ f(4)=\frac{1}{2} \ln \left(\frac{17}{19}\right)$
A
2
B
$2(e-1)$
C
$2 e-1$
D
$e(e-1)$
Solution
For $x \leq 0$
$f(x)=\int\limits_0^2 e^{t-x} d t=e^{-x}\left(e^2-1\right)$
For $0 < x < 2$
$f(x)=\int\limits_0^x e^{x-t} d t+\int_x^2 e^{t-x} d t=e^x+e^{2-x}-2$
For $x \geq 2$
$f(x)=\int\limits_0^2 e^{x-t} d t=e^{x-2}\left(e^2-1\right)$
For $x \leq 0, f(x)$ is $\downarrow$ and $x \geq 2, f(x)$ is $\uparrow$
$\therefore$ Minimum value of $f ( x )$ lies in $x \in(0,2)$
Applying $A . M \geq G . M$,
minimum value of $f(x)$ is $2(e-1)$
A
Only (I) is true
B
Both (I) and (II) are true
C
Neither (I) nor (II) is true
D
Only (II) is true
Solution
$ g ( x )= f (- x )- f ( x )=\frac{1+ e ^{ x }}{1- e ^{ x }} $
$ \Rightarrow g ^{\prime}( x )=\frac{2 e ^{ x }}{\left(1- e ^{ x }\right)^2}>0$
$ \Rightarrow g \text { is increasing in }(0,1)$
$ \Rightarrow g \text { is one-one in }(0,1)$
A
straight line with the sum of its intercepts on the coordinate axes equals $-18$
B
hyperbola with eccentricity 2
C
hyperbola with the length of the transverse axis 7
D
straight line with the sum of its intercepts on the coordinate axes equals 14
Solution
$ \left(( x -2)^2+( y -3)^2\right)-\left(( x -3)^2-( y -4)^2\right)=1+1 $
$\Rightarrow x + y =7$
A
$5 \sqrt{3}$
B
$\frac{14}{3}$
C
$\frac{1}{3}$
D
5
Solution
For
$y ^2=\frac{ x }{2}, T : y = mx +\frac{1}{8 m }$
For tangent to $y^2+1=x$
$\Rightarrow\left( mx +\frac{1}{8 m }\right)^2+1=x $
$D =0 \Rightarrow m =\frac{1}{2 \sqrt{2}} $
$\therefore T : x -2 \sqrt{2} y +1=0 $
$d =\left|\frac{6+8+1}{\sqrt{9}}\right|=5$
A
$4^8$
B
$2^8$
C
$2^4$
D
$6^4$
Solution
$|A|=\frac{1}{\log x \cdot \log y \cdot \log z} \begin{vmatrix} \log x & \log y & \log z \\ \log x & 2 \log y & \log z \\ \log x & \log y & 3 \log z\end{vmatrix}=2$
$\Rightarrow\left|\operatorname{adj}\left(\operatorname{adj} A^2\right)\right|=\left|A^2\right|^4=2^8$
A
976
B
944
C
496
D
464
Solution
$ y=\frac{1-x^{32}}{1-x} \Rightarrow y-x y=1-x^{32} $
$ y^{\prime}-x y^{\prime}-y=-32 x^{31}$
$ y^{\prime \prime}-x y^{\prime \prime}-y^{\prime}-y^{\prime}=-(32)(31) x^{30} $
at $ x=-1 \Rightarrow y^{\prime}-y^{\prime \prime}=496$
A
$\frac{15}{44}$
B
$\frac{1}{3}$
C
$\frac{7}{22}$
D
$\frac{1}{5}$
Solution
$M=33 \times 33$
$ x(66-x) \geq \frac{5}{9} \times 33 \times 33 $
$ 11 \leq x \leq 55$
$ A:\{12,15,18, \ldots 54\} $
$ P(A)=\frac{15}{45}=\frac{1}{3}$
A
$3 \sqrt{2}$
B
4
C
$2 \sqrt{6}$
D
$4 \sqrt{3}$
Solution
Let $P =(2 \lambda+1, \lambda+3,2 \lambda+2)$
Let $Q=(\mu+2,2 \mu+2,3 \mu+3)$
$ \Rightarrow \frac{2 \lambda-\mu-1}{1}=\frac{\lambda-2 \mu+1}{-1}=\frac{2 \lambda-3 \mu-1}{-2} $
$\Rightarrow \lambda=\mu=3 \Rightarrow P (7,6,8) \text { and } Q (5,8,12) $
$ PQ =2 \sqrt{6}$
A
$S_1=\Phi$ and $S_2=R-\{0\}$
B
$S_1$ is an infinite set and $n\left(S_2\right)=2$
C
$S_1=R-\{0\}$ and $S_2=\Phi$
D
$n \left( S _1\right)=2$ and $S _2$ is an infinite set
Solution
$ \Delta=\begin{vmatrix}a & 2 a & -3 a \\ 2 a+1 & 2 a+3 & a+1 \\ 3 a+5 & a+5 & a+2\end{vmatrix} $
$ =a\left(15 a^2+31 a+36\right)=0 \Rightarrow a=0 $
$ \Delta \neq 0 \text { for all } a \in R-\{0\} $
Hence $ S_1=R-\{0\} S_2=\Phi$
A
$2 \sqrt{3}$
B
$\sqrt{14}$
C
3
D
$\sqrt{6}$
Solution

Equation of line is $\frac{ x +3}{3}=\frac{ y -2}{3}=\frac{ z -3}{-1}=\lambda$
$M (3 \lambda-3,3 \lambda+2,3-\lambda)$
D.R of PM( $3 \lambda-7,3 \lambda-4,5-\lambda)$
Since PM is perpendicular to line
$ \Rightarrow 3(3 \lambda-7)+3(3 \lambda-4)-1(5-\lambda)=0 $
$ \Rightarrow \lambda=2$
$ \Rightarrow M (3,8,1) \Rightarrow PM =\sqrt{14}$
A
$x^2+y^2+3 x+3 y+4=0$
B
$x^2+y^2+5 x+5 y+12=0$
C
$x^2+y^2+3 x+5 y+8=0$
D
$x^2+y^2-5 x-5 y+12=0$
Solution
Only possibility $\alpha=0, \beta=1$
$\therefore$ equation of circle $x ^2+ y ^2- x - y =0$
Image of circle in $x+y+2=0$ is
$x^2+y^2+5 x+5 y+12=0$
A
$3 \sqrt{2}$
B
1
C
$2 \sqrt{3}$
D
$\sqrt{6}$
Solution
$ \vec{ b }=\lambda \vec{ a } \times(\vec{ a } \times \hat{ j }) $
$\Rightarrow \vec{ b }=\lambda(-2 \hat{ i }-2 \hat{ j }+2 \hat{ k }) $
$ |\vec{ b }|=|\vec{ a }| \therefore \sqrt{6}=\sqrt{12}|\lambda| \Rightarrow \lambda=\pm \frac{1}{\sqrt{2}}$
$ \left(\lambda=\frac{1}{\sqrt{2}} \text { rejected } \because \vec{ b } \text { makes acute angle with y axis }\right) $
$ \vec{ b }=-\sqrt{2}(-\hat{ i }-\hat{ j }+\hat{ k })$
$ \frac{(3 \vec{ a }+\sqrt{2} \vec{ b }) \cdot \vec{ c }}{|\vec{ c }|}=3 \sqrt{2}$
A
equivalent to $p \vee q$
B
equivalent to $(-p) \vee(-q)$
C
a contradiction
D
a tautology
Solution
$( p \wedge \sim q ) \rightarrow( p \rightarrow \sim q ) $
$ \equiv(\sim( p \wedge \sim q )) \vee(\sim p \vee \sim q ) $
$ \equiv(\sim p \vee q ) \vee(\sim p \vee \sim q )$
$ \equiv \sim p \vee t \equiv t $
A
$18 \sqrt{6}-\frac{33}{2}$
B
$12 \sqrt{6}-\frac{33}{2}$
C
$12 \sqrt{6}-\frac{31}{2}$
D
$18 \sqrt{6}-\frac{31}{2}$
Solution
$f^{\prime}(x)=8 x^3-36 x+8=4\left(2 x^3-9 x+2\right) $
$ f^{\prime}(x)=0 $
$ \therefore x=\frac{\sqrt{6}-2}{2}$
Now
$f(x)=\left(x^2-2 x-\frac{9}{2}\right)\left(2 x^2+4 x-1\right)+24 x+7.5 $
$ \therefore f\left(\frac{\sqrt{6}-2}{2}\right)=M=12 \sqrt{6}-\frac{33}{2}$
A
$3(\sqrt{2}+1)$
B
$\frac{3}{2}(\sqrt{2}+1)$
C
$\frac{\sqrt{2}+1}{2}$
D
$\frac{3}{2 \sqrt{2}}$
Solution
$ \underset{n \rightarrow \infty}{Lim} \frac{0+3+6+9+\ldots . n \text { terms }}{\sqrt{2 n^4+4 n+3}-\sqrt{n^4+5 n+4}} $
$ \underset{n \rightarrow \infty}{Lim} \frac{3 n(n-1)}{2\left(\sqrt{2 n^4+4 n+3}-\sqrt{n^4+5 n+4}\right)} $
$=\frac{3}{2(\sqrt{2}-1)}=\frac{3}{2}(\sqrt{2}+1)$
A
$\frac{3}{4}$
B
$\frac{1}{2}$
C
$-\frac{1}{4}$
D
$\frac{1}{4}$
Solution
$ (\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{ c }=\frac{\vec{b}-\vec{c}}{2} $
$ \vec{a} \cdot \vec{c}=\frac{1}{2}, \vec{a} \cdot \vec{b}=\frac{1}{2}$
$\therefore \vec{b} \cdot \vec{d}=\frac{1}{2}$
$ (\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d})=\vec{a} \cdot(\vec{b} \times(\vec{c} \times \vec{d})) $
$ =\vec{a} \cdot((\vec{b} \cdot \vec{d}) \vec{c}-(\vec{b} \cdot \vec{c}) \vec{d})$
$ =(\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d})=\frac{1}{4}$
Answer: 216
Solution

$H : \frac{ x ^2}{36}-\frac{y^2}{9}=1$
equation of normal is $6 x \cos \theta+3 y \cot \theta=45$
$\text { slope }=-2 \sin \theta=-\sqrt{2} $
$ \Rightarrow \theta=\frac{\pi}{4}$
Equation of normal is $\sqrt{2} x + y =15$
$P :( a \sec \theta, b \tan \theta)$
$\Rightarrow P (6 \sqrt{2}, 3)$ and $K (0,15)$
$d^2=216$
Answer: 9
Solution
Equation of plane is
$ ( x -2 y - z -5)+ b ( x + y +3 z -5)=0 $
$ \begin{vmatrix} 1+ b & -2+ b & -1+3 b \\1 & 1 & 2 \\2 & 3 & 1\end{vmatrix}=0$
$\Rightarrow b =12 $
$ \therefore \text { plane is } 13 x +10 y +35 z =65$
Distance from given point to plane $=9$
Answer: 600
Solution

$ \text { Area }=2 \int\limits^2\left(x^2+6-\frac{5 x^2}{2}\right) d x=\int\limits_0^{\frac{2 \alpha}{5}}\left(\alpha x-\frac{5 x^2}{2}\right) d x$
$ \Rightarrow \int\limits_0^{\frac{2 \alpha}{5}}\left(\alpha x-\frac{5 x^2}{2}\right) d x=16 $
$ \Rightarrow \alpha^3=600$
Answer: 2039
Solution
Let $f \circ g(x)=h(x)$
$ \Rightarrow h^{-1}(x)=\left(\frac{x-7}{2}\right)^{\frac{1}{3}} $
$\Rightarrow h(x)=\text { fog }(x)=2 x^3+7$
$ \text { fog }(x)=a\left(x^{ b }+ c \right)-3 $
$ \Rightarrow a =2, b =3, c =5$
$ \Rightarrow \operatorname{fog}( ac )= fog (10)=2007$
$ g \left( f ( x )=(2 x -3)^3+5\right. $
$ \Rightarrow \operatorname{gof}( b )=\operatorname{gof}(3)=32$
$ \Rightarrow \operatorname{sum}=2039$
Answer: 2
Solution
Case $I : x >0$
$ \tan ^{-1} \frac{2 x}{1-x^2}+\tan ^{-1} \frac{2 x}{1-x^2}=\frac{\pi}{3}$
$x=2-\sqrt{3}$
Case II : $x < 0$
$ \tan ^{-1} \frac{2 x}{1-x^2}+\tan ^{-1} \frac{2 x}{1-x^2}+\pi=\frac{\pi}{3} $
$x=\frac{-1}{\sqrt{3}} \Rightarrow \alpha=2$
Answer: 495
Solution
$ \begin{vmatrix} A +6 d & 7 & 1 \\ 2( A +1+8 d ) & 17 & 1 \\ A +2+16 d & 17 & 1\end{vmatrix}+70=0$
$ \Rightarrow A =-7 \text { and } d =6 $
$ \therefore c - a - b =20$
$ S _{20}=495$
Answer: 43
Solution
Elements of the type $3 k =3$
Elements of the type $3 k +1=1,7,9$
Elements of the type $3 k +2=2,5,11$
Subsets containing one element $S_1=1$
Subsets containing two elements
$S _2={ }^3 C _1 \times{ }^3 C _1=9$
Subsets containing three elements
$S _3={ }^3 C _1 \times{ }^3 C _1+1+1=11$
Subsets containing four elements
$S _4={ }^3 C _3+{ }^3 C _3+{ }^3 C _2 \times{ }^3 C _2=11$
Subsets containing five elements
$S _5={ }^3 C _2 \times{ }^3 C _2 \times 1=9$
Subsets containing six elements $S_6=1$
Subsets containing seven elements $S _7=1$
$\Rightarrow \text { sum }=43$
Answer: 1080
Solution
General term is $\sum \frac{5 !(2 x)^{n_1}\left(x^{-7}\right)^{n_2}\left(3 x^2\right)^{n_3}}{n_{1} ! n_{2} ! n_{3} !}$
For constant term,
$n _1+2 n _3=7 n _2$
$\& n _1+ n _2+ n _3=5$
Only possibility $n _1=1, n _2=1, n _3=3$
$\Rightarrow$ constant term $=1080$
Answer: 25