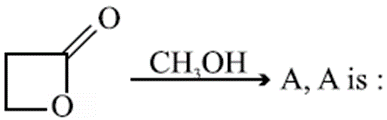
Question

The rapid change of pH near the stoichiometric point of an acid-base titration is the basis of indicator detection. pH of the solution is related to ratio of the concentration of the conjugate acid (HIn) and base $\left(\right.In^{-}\left.\right)$ forms of the indicator by the expression

• A. $log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}=pK_{l n}-pH$
• B. $log\frac{\left[\right. H I n \left]\right.}{\left[\right. I n^{-} \left]\right.}=pK_{l n}-pH$
• C. $log\frac{\left[\right. H I n \left]\right.}{\left[\right. I n^{-} \left]\right.}=pH-pK_{l n}$
• D. $log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}=pH-pK_{l n}$

Answer 1

Answer: (D)

Let us consider the formation of a salt of a weak acid and a strong base.
$In^{-}+H_{2}O\rightleftharpoonsHIn+OH^{-}$
$K_{h}\frac{\left[\right. H I n \left]\right. \left[\right. O H^{-} \left]\right.}{\left[\right. I n^{-} \left]\right.}$ …(i)
Other equations present in the solution are
$HIn\rightleftharpoonsH^{+}+In^{-}$
$H_{2}O\rightleftharpoonsH^{+}+OH^{-}$
$K_{I n}=\frac{\left[\right. H^{+} \left]\right. \left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$ …(ii)
$K_{w}=\left[\right.H^{+}\left]\right.\left[\right.OH^{-}\left]\right.$ …(iii)
From (ii) and (iii),
$\frac{K_{w}}{K_{I n}}\frac{\left[\right. H I n \left]\right. \left[\right. O H^{-} \left]\right.}{\left[\right. I n^{-} \left]\right.}=K_{h}$
$\left[\right.OH^{-}\left]\right.=\frac{K_{w}}{K_{I n}}\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$
$log\left[\right.OH^{-}\left]\right.=logK_{w}-logK_{I n}+log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$
$-pOH=-pK_{w}+pK_{I n}+log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$
$pK_{w}-pOH=pK_{I n}+log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$
or, $pH=pK_{I n}+log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}$
i.e. $log\frac{\left[\right. I n^{-} \left]\right.}{\left[\right. H I n \left]\right.}=pH-pK_{I n}$