1. Tardigrade
  2. Question
  3. Mathematics
  4. Let P a point on y2=4x such that its focal distance is 4. Let T be the point of intersection of tangents drawn at P and vertex of the parabola. If S is focus and 'R' is an interior point on the axis of the parabola at a distance 4 unit from S, then area of quadrilateral PRST is equal to

Q. Let $P$ a point on $y^{2}=4x$ such that its focal distance is $4.$ Let $T$ be the point of intersection of tangents drawn at $P$ and vertex of the parabola. If $S$ is focus and $'R'$ is an interior point on the axis of the parabola at a distance $4$ unit from $S,$ then area of quadrilateral $PRST$ is equal to

NTA AbhyasNTA Abhyas 2022 Report Error

Solution:

$P\left(a t^{2} , \, 2 a t\right)=P\left(t^{2} , \, 2 t\right)$
$⇒4=1+t^{2}⇒t^{2}=3$
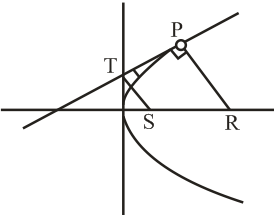
  • ​​​​​​​ Solution
$T\left(\right.0, \, \sqrt{3}\left.\right), \, S\left(\right.1, \, 0\left.\right), \, P\left(\right.3, \, 2\sqrt{3}\left.\right), \, R\left(\right.5, \, 0\left.\right)$
Required area $=6\sqrt{3}$

Questions from NTA Abhyas 2022

1. Let points $A_{1},A_{2}$ and $A_{3}$ lie on the parabola $y^{2}=8x.$ If $\Delta A_{1}A_{2}A_{3}$ is an equilateral triangle and normals at points $A_{1},A_{2}$ and $A_{3}$ on this parabola meet at the point $\left(h , 0\right)$ , then the value of $h$ is

2. The lines represented by the equation $x^{2}+2\sqrt{3}xy+3y^{2}-3x-3\sqrt{3}y-4=0$ , are

Straight Lines

3. If the roots of the equation $ax^{2}+bx+c=0$ are in the ratio $m:n$ , then

Complex Numbers and Quadratic Equations

4. If $a,b,c,d,e,f$ are in arithmetic progression. Then $e - c$ is equal to

Sequences and Series

5. The sum to $n$ terms of $\left[\frac{1}{1.3} + \frac{2}{1.3 . 5} + \frac{3}{1.3 . 5.7} + \frac{4}{1.3 . 5.7 . 9} + . . . . . . . .\right]$ is

Mathematics Most Viewed Questions

1. The solution of $\frac{dy}{dx} = \frac{y}{x}+\tan \frac{y}{x}$ is

WBJEE 2011 Differential Equations

2. The solution of the differential equation $\frac{dy}{dx} = (x +y)^2$ is

COMEDK 2009 Differential Equations

3. $\int\frac{1}{\sin x\, \cos x}$ dx is equal to

KEAM 2016 Integrals

4. If $\begin{bmatrix}1&- \tan\theta \\ \tan \theta&1\end{bmatrix}\begin{bmatrix}1&\tan \theta \\ - \tan \theta &1\end{bmatrix}^{-1} = \begin{bmatrix}a&-b\\ b&a\end{bmatrix}$ then

COMEDK 2009 Matrices

5. The value of $ \int{\frac{{{x}^{2}}+1}{{{x}^{4}}-{{x}^{2}}+1}}dx $ is

KEAM 2007 Integrals

Latest Updates