- Tardigrade
- Question
- Physics
- Two objects are connected by a light string passing over a light, frictionless pulley as shown in the figure. The object of mass m1=5.0 kg is released from rest at a height h=4.0 m above the table. Find the maximum height above the table to which the 3.0- kg object rises (in m ).
Q.
Two objects are connected by a light string passing over a light, frictionless pulley as shown in the figure. The object of mass $m_{1}=5.0\, kg$ is released from rest at a height $h=4.0\, m$ above the table. Find the maximum height above the table to which the $3.0- kg$ object rises (in $m$ ).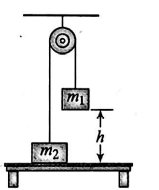
Work, Energy and Power
Report Error
Solution:
We assign height $y=0$ to the table top.
Using conservation of energy for the system of the Earth and the two objects:

Then total mechanical energy of the system remains constant and the energy version of the isolated system model gives
$\left(K_{A}+K_{B}+U_{g}\right)_{i}=\left(K_{A}+K_{B}+U_{g}\right)_{f a}$
At the initial point, $K_{A i}$ and $K_{B i}$ are zero and we define the gravitational potential energy of the system as zero. Thus the total initial energy is zero, and we have
$0=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{f a}^{2}+m_{2} g h+m_{1} g(-h)$
Here we have used the fact that because the cord does not stretch, the two blocks have the same speed. The heavier mass moves down, losing gravitational potential energy, as the lighter mass moves up, gaining gravitational potential energy.
Simplifying, $\left(m_{1}-m_{2}\right) g h=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{f a}^{2}$
$\Rightarrow v_{f a}=\sqrt{\frac{2\left(m_{1}-m_{2}\right) g h}{\left(m_{1}+m_{2}\right)}}$
$=\sqrt{\frac{2(5.0 kg -3.0 kg ) 10(4.0 m )}{(5.0 kg +3.0 kg )}}=\sqrt{20} m / s$
Now we apply conservation of mechanical energy for the system of the $3.0- kg$ object and the Earth during the time interval between the instant when the string goes slack and the instant at which the $3.0- kg$ object reaches its highest position in its free fall.
$\Delta K+\Delta U=0$
$\Rightarrow \Delta K=-\Delta U$
$0-\frac{1}{2} m_{2} v^{2}=-m_{2} g \Delta v$
$\Rightarrow \Delta y=\frac{v^{2}}{2 g}=1.0\, m$
Hence, $y_{\max }=4.0 m +\Delta y=5.0\,m$
Questions from Work, Energy and Power
Physics Most Viewed Questions
1. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
2. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
3. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023