Q.
Two objects are connected by a light string passing over a light, frictionless pulley as shown in the figure. The object of mass $m_{1}=5.0\, kg$ is released from rest at a height $h=4.0\, m$ above the table. Find the maximum height above the table to which the $3.0- kg$ object rises (in $m$ ).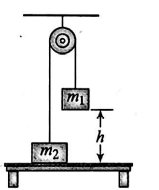
Work, Energy and Power
Solution:
