- Tardigrade
- Question
- Physics
- In the arrangement shown in the figure, the system is in equilibrium. Mass of the block A is M and that of the insect clinging to block B is m. Pulley and string are light. The insect loses contact with the block B and begins to fall. After how much time the insect and the block B will have a separation L between them.
Q.
In the arrangement shown in the figure, the system is in equilibrium. Mass of the block $A$ is $M$ and that of the insect clinging to block $B$ is $m$. Pulley and string are light. The insect loses contact with the block $B$ and begins to fall. After how much time the insect and the block $B$ will have a separation $L$ between them.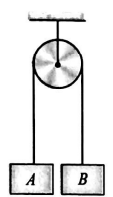
Laws of Motion
Report Error
Solution:
Mass of block $A: m_A=M$
Mass of block $B ; m_B=M-m$
Acceleration of $B$ after the insect falls,
$a_B=\left(\frac{m_A-m_B}{m_A+m_B}\right) g(\uparrow)=\frac{m g}{2 M-m}$
Acceleration of the insect $=g(\downarrow)$
The two objects separate with a relative acceleration of
$ a=g+\frac{m g}{2 M-m}=\frac{2 M g}{2 M-m} $
$ \therefore \frac{1}{2} a t^2=L$
$\left(\frac{M g}{2 M-m}\right) t^2=L $
$ \Rightarrow t=\sqrt{\frac{(2 M-m) L}{M g}}$
Questions from Laws of Motion
Physics Most Viewed Questions
1. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
2. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
3. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023