Q.
In the arrangement shown in the figure, the system is in equilibrium. Mass of the block $A$ is $M$ and that of the insect clinging to block $B$ is $m$. Pulley and string are light. The insect loses contact with the block $B$ and begins to fall. After how much time the insect and the block $B$ will have a separation $L$ between them.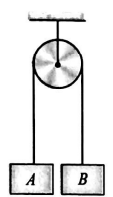
Laws of Motion
Solution: