1. Tardigrade
  2. Question
  3. Physics
  4. In previous question what is the minimum possible value of kinetic energy of the neutrons for this to be possible. The mass of neutron and proton can be assumed to be nearly same. Use h c=12400 eV mathringA.

Q. In previous question what is the minimum possible value of kinetic energy of the neutrons for this to be possible. The mass of neutron and proton can be assumed to be nearly same. Use $h c=12400\, eV\,\mathring{A}$.

Atoms Report Error

Solution:

Let $u$ be the speed of neutron before collision
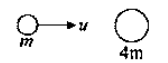
image
At end of the deformation phase (when the kinetic energy of (neutron + $He^+$) system is least)
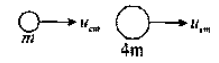
image
Where $u_{cm}$ is velocity of centre of mass. From conservation of momentum
$u_{ cm }=\frac{m u}{m+4 m}=\frac{u}{5}$
The loss of kinetic energy
$\Delta K=\frac{1}{2} m u^{2}-\frac{1}{2} n\left(\frac{u}{5}\right)^{2}-\frac{1}{2} 4 m\left(\frac{u}{5}\right)^{2}$
$\Rightarrow \Delta K=\frac{4}{5}\left(\frac{1}{2} m u^{2}\right)$
It $K$ is the kinetic energy of neutron then the maximum loss in K.E. of system is
$\frac{4}{5} K=12.75 \times 4=51\, eV$
or $K=\frac{51 \times 5}{4}=63.75\, eV$

Questions from Atoms

1. The transition from the state $n = 4$ to $n = 3$ in a hydrogen like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from

AIEEE 2009

2. Muon $ (\mu^{-})$ is a negatively charged $(|q | = |e|$ particle with a mass $m_{\mu} = 200$ me, where me is the mass of the electron and e is the electronic charge. If $\mu$- is bound to a proton to form a hydrogen like atom, identify the correct statements.
(A) Radius of the muonic orbit is $200$ times smaller than that of the electron.
(B) The speed of the $\mu^{-}$ in the $n^{th}$ orbit is $\frac{1}{200}$ times that of the electron in the $n^{th}$ orbit.
(C) The ionization energy of muonic atom is $200$ times more than that of an hydrogen atom.
(D) The momentum of the muon in the $n^{th}$ orbit is $200 $ times more than that of the electron.

JEE Main 2018

3. The ratio of the wavelengths for $2 \rightarrow 1$ transition in $Li^{2 +}, \, \text{He}^{+}$ and $H$ is

NTA Abhyas 2020

4. Ionization energy of $He^{+}$ ion at minimum energy position is

NTA Abhyas 2020

5. The ratio of kinetic energy and the total energy of the electron in the $n^{th}$ quantum state of Bohr's atomic model of a hydrogen atom is

NTA Abhyas 2020

Physics Most Viewed Questions

1. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$

NEET 2021 Motion in a Straight Line

2. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:

NEET 2021 Physical World, Units and Measurements

3. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly

NEET 2020 Dual Nature of Radiation and Matter

4. A wheel with $20$ metallic spokes each $1\, m$ long is rotated with a speed of $120\, rpm$ in a plane perpendicular to a magnetic field of $0.4\, G$. The induced emf between the axle and rim of the wheel will be, $(1 G = 10^{-4}\, T)$

NEET 2020 Electromagnetic Induction

5. Calculate the acceleration of the block and trolly system shown in the figure The coefficient of kinetic friction between the trolly and the surface is $0.05. (g = 10 \,m/s^{2}$, mass of the string is negligible and no other friction exists
image

NEET 2020 Laws of Motion

Latest Updates