- Tardigrade
- Question
- Physics
- In a cylindrical container of sufficiently large height, two easily moving pistons enclose certain amount of same ideal gas in two chambers as shown in the figure-2.43. <img class=img-fluid question-image alt=image src=https://cdn.tardigrade.in/img/question/physics/b00eb554dfb6a2d04c8585e9a3bd107a-.png /> The upper piston is at a height 20 cm from the bottom and lower piston is at a height 8 cm from the bottom. The mass of each piston is m kg and cross sectional area of each piston is A m2 where (m g/A)=P0 and P0 is the atmospheric pressure =1 × 105 N / m 2. The cylindrical container and pistons are made of conducting material. Initially the temperature of gas is 27° C and whole system is in equilibrium. Now if the upper piston is slowly lifted by 16 cm and held in that position with the help of some external force. As a result, the lower piston rises slowly by l cm. In a cylindrical container of sufficiently large height, two easily moving pistons enclose certain amount of same ideal gas in two chambers as shown in the figure-2.43. <img class=img-fluid question-image alt=image src=https://cdn.tardigrade.in/img/question/physics/b00eb554dfb6a2d04c8585e9a3bd107a-.png /> The upper piston is at a height 20 cm from the bottom and lower piston is at a height 8 cm from the bottom. The mass of each piston is m kg and cross sectional area of each piston is A m2 where (m g/A)=P0 and P0 is the atmospheric pressure =1 × 105 N / m 2. The cylindrical container and pistons are made of conducting material. Initially the temperature of gas is 27° C and whole system is in equilibrium. Now if the upper piston is slowly lifted by 16 cm and held in that position with the help of some external force. As a result, the lower piston rises slowly by l cm. The value of l is :
Q.
In a cylindrical container of sufficiently large height, two easily moving pistons enclose certain amount of same ideal gas in two chambers as shown in the figure-2.43.
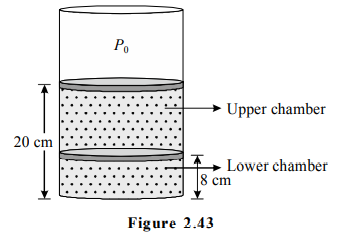
The upper piston is at a height $20\, cm$ from the bottom and lower piston is at a height $8\, cm$ from the bottom. The mass of each piston is m kg and cross sectional area of each piston is $A\, m^2$ where $\frac{m g}{A}=P_{0}$ and $P_{0}$ is the atmospheric pressure $=1 \times 10^{5} N / m ^{2}$.
The cylindrical container and pistons are made of conducting material. Initially the temperature of gas is $27^{\circ} C$ and whole system is in equilibrium. Now if the upper piston is slowly lifted by $16\, cm$ and held in that position with the help of some external force. As a result, the lower piston rises slowly by $l\, cm$.
In a cylindrical container of sufficiently large height, two easily moving pistons enclose certain amount of same ideal gas in two chambers as shown in the figure-2.43.

The upper piston is at a height $20\, cm$ from the bottom and lower piston is at a height $8\, cm$ from the bottom. The mass of each piston is m kg and cross sectional area of each piston is $A\, m^2$ where $\frac{m g}{A}=P_{0}$ and $P_{0}$ is the atmospheric pressure $=1 \times 10^{5} N / m ^{2}$.
The cylindrical container and pistons are made of conducting material. Initially the temperature of gas is $27^{\circ} C$ and whole system is in equilibrium. Now if the upper piston is slowly lifted by $16\, cm$ and held in that position with the help of some external force. As a result, the lower piston rises slowly by $l\, cm$.
The value of $l$ is :
Kinetic Theory
Report Error
Solution:
Let $P_{1}$ and $P_{2}$ be the initial pressure in lower chamber of gas and upper chamber of gas.
$P_{2}=P_{0}+\frac{m g}{A}=2 P_{0}, V_{2}=A \times 12 \times 10^{-2} m ^{3}$
If $P_{2}^{\prime}$ and $V_{2}^{\prime}$ are final pressure and volume in upper chamber
$V_{2}^{\prime} =A \times(28-l) \times 10^{-2} m ^{3}$
$P_{2} V_{2} =P_{2}^{\prime} V_{2}^{\prime}$
$\Rightarrow P_{2}^{\prime}=\frac{P_{2} V_{2}}{P_{2}^{\prime}}=\frac{24 P_{0}}{28-l}$
Now consider lower chamber
$P_{1} =P_{0}+\frac{2 m g}{A}=3 P_{0}$
and $V_{1} =A \times 8 \times 10^{-2} m ^{3}$
$P_{1}^{\prime} =P_{2}^{\prime}+\frac{m g}{A}=P_{0}\left[\frac{52-l}{28-l}\right]$
and $V_{1}^{\prime} =A \times(8+l) \times 10^{-2} m ^{3}$
$P_{1} V_{1} =P_{1}^{\prime} V_{1}^{\prime}$
$3 P_{0} A \times 8 \times 10^{-2} =P_{0}\left[\frac{52-l}{28-l}\right] \times A \times(8+l) \times 10^{-2}$
$24 =\left[\frac{52-l}{28-l}\right] \times(8+l)$
Solving we get $l=4\, cm$
$\Rightarrow P_{1}^{\prime}=2 P_{0}=2 \times 10^{5} A / m ^{2}$
$\Rightarrow P_{2}^{\prime}=\frac{24 P_{0}}{28-l}=P_{0}=1 \times 10^{5} N / m ^{2}$
$\frac{V_{2}^{\prime}}{V_{1}^{\prime}}=\frac{28-l}{8+l}=\frac{24}{12}=2$
Questions from Kinetic Theory
Physics Most Viewed Questions
1. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
2. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
3. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023