- Tardigrade
- Question
- Physics
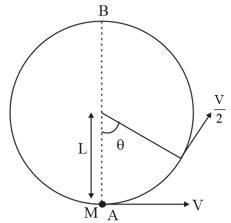
- A rod of length ℓ rotates with a uniform angular velocity ω about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction B with its direction parallel to the axis of rotation. The induced emf between the two ends of the rods is-
Q. A rod of length $\ell $ rotates with a uniform angular velocity $\omega $ about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction $B$ with its direction parallel to the axis of rotation. The induced emf between the two ends of the rods is-
Solution:
Length of the rod between the axis of rotation
and one end of the rod
$=L/2$ Area swept out in one rotation
$=\pi \left(\right.L/2\left(\left.\right)^{2}=\left(\pi L^{2} / 4\right)$
Angular velocity $=\omega $ radian/sec
Frequency $n$ of revolution $=\frac{\omega }{2 \pi }$
Area swept out per second $=\frac{\pi L^{2}}{4}\left(\frac{\omega }{2 \pi }\right)=\frac{L^{2} \omega }{8}$
Magnetic Induction $=B$
Rate of change of magnetic flux $=\left(B L^{2} \omega / 8\right)$
Numerical value of induced $emf=BL^{2}\omega /8.$
Numerical value of induced emf between the axis and the other end is also $\left(B L^{2} \omega / 8\right).$ These two emf are in opposite directions. Hence, the potential difference between the two ends of the rod is zero.
Hence, the correct answer is option $\left(\right.2\left.\right).$
Questions from NTA Abhyas 2020
2. The velocity displacement graph of a particle moving along a straight line is -

The most suitable acceleration-displacement graph will be
Motion in a Straight Line
3. A drum of radius $R$ and mass $M$ rolls down without slipping along an inclined plane of angle $\theta $ . The frictional force
System of Particles and Rotational Motion
Physics Most Viewed Questions
1. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
2. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
3. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023