- Tardigrade
- Question
- Physics
- A block of mass m is placed on the top of a 6 kg cart such that the time period of the system is 0.75 s assuming there is no slipping. If the cart is displaced by 50 mm from its equilibrium position and released, then the coefficient of static friction μ s between block and cart is just sufficient to prevent the block from sliding. The value of m and μ s respectively are (Take g=9.8 m/s2 ) <img class=img-fluid question-image alt=Question src=https://cdn.tardigrade.in/q/nta/p-kizw6soltmai.png />
Q.
A block of mass $m$ is placed on the top of a $6 \, kg$ cart such that the time period of the system is $0.75 \, s$ assuming there is no slipping. If the cart is displaced by $50 \, mm$ from its equilibrium position and released, then the coefficient of static friction $\mu _{s}$ between block and cart is just sufficient to prevent the block from sliding. The value of $m$ and $\mu _{s}$ respectively are (Take $g=9.8 \, m/s^{2}$ )
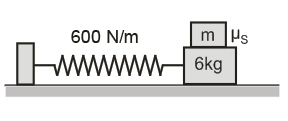
Solution:
$ \text{T} = 2 \pi \sqrt{\frac{\text{m} + 6}{\text{600}}} \, \, \, \left(\right. \text{T} = 2 \pi \sqrt{\frac{\text{m}}{\text{k}}} \left.\right)$
$\text{or} \text{0.75} = 2 \pi \sqrt{\frac{\text{m} + 6}{\text{600}}}$
$\therefore \quad \mathrm{m}=\frac{(0.75)^2 \times 600}{(2 \pi)^2}-6$
= 2.55 kg
Maximum acceleration of SHM is,
amax = ω2A (A = amplitude)
i.e., maximum force on mass 'm' is m ω2 A which is being provided by the force of friction between the mass and the cart. Therefore,
$\mu_{\mathrm{s}} \mathrm{mg} \geq \mathrm{m} \omega^2 \mathrm{~A}$
$
or $\mu_{ s } \geq \frac{\omega^{2} A }{ g }$
Or $\mu_{ s } \geq\left(\frac{2 \pi}{ T }\right)^{2} \cdot \frac{ A }{ g }$
Or $\mu_{ s } \geq\left(\frac{2 \pi}{0.75}\right)^{2}\left(\frac{0.05}{9.8}\right) \quad( A =50 mm )$
Or $\mu_{ s } \geq 0.358$
Thus, the minimum value of $\mu_{ s }$ should be 0.358
Questions from NTA Abhyas 2020
2. Two long straight conductors with current $I_{1}$ and $I_{2}$ are placed along $X$ and $Y$ axes. The equation of locus of point of zero magnetic induction is -
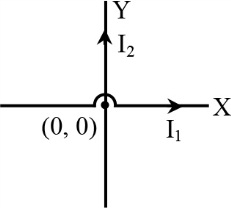
Moving Charges and Magnetism
Questions from Oscillations
1. Infinite springs with force constants $k,\, 2k,\, 4k$ and $8k...$ respectively are connected in series. The effective force constant of the spring will be
J & K CET 2004
Physics Most Viewed Questions
1. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
2. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
3. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023

