- Tardigrade
- Question
- Physics
- The current through the solenoid is changing in such way that flux through it is given by φ = ϵ textt . The solenoid is surrounded by a loop having resistance textR text1 and textR text2 as shown. Then the reading of the two voltmeters V1 and V2 differ by: <img class=img-fluid question-image alt=Question src=https://cdn.tardigrade.in/q/nta/p-spssilzgowpwsohi.jpg />
Q.
The current through the solenoid is changing in such way that flux through it is given by $\phi = \epsilon \text{t}$ . The solenoid is surrounded by a loop having resistance $\text{R}_{\text{1}}$ and $\text{R}_{\text{2}}$ as shown. Then the reading of the two voltmeters $V_{1}$ and $V_{2}$ differ by :
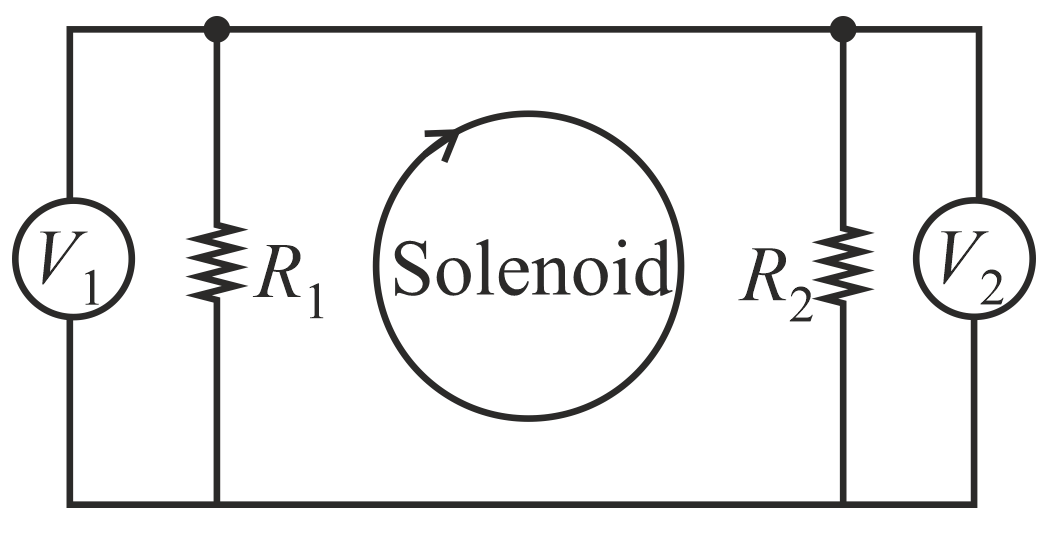
Solution:
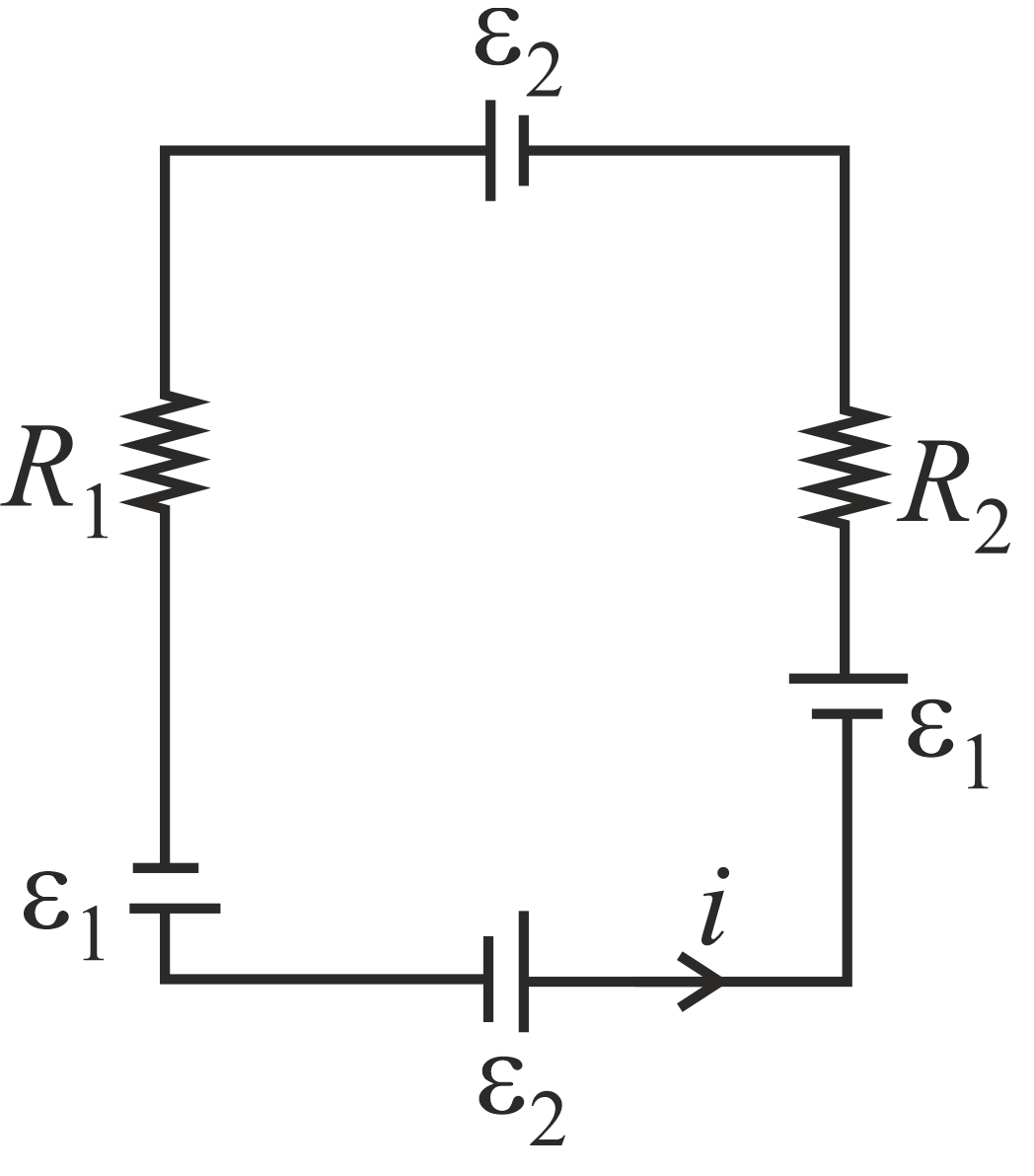
$\text{i} = \frac{2 \epsilon _{1} + 2 \epsilon _{2}}{\text{R}_{1} + \text{R}_{2}} = \frac{\epsilon }{\text{R}_{1} + \text{R}_{2}}$
Where $\epsilon = \frac{\text{d} \phi}{\text{dt}}$ is the net emf in the circuit
$\therefore \left(\text{V}\right)_{1} - \left(\text{V}\right)_{2} = \left(\left(\epsilon \right)_{1} - \left(\text{iR}\right)_{1}\right) - \left(\left(\epsilon \right)_{1} - \left(\text{iR}\right)_{2}\right) = \frac{\epsilon \left(\left(\text{R}\right)_{2} - \left(\text{R}\right)_{1}\right)}{\left(\text{R}\right)_{1} + \left(\text{R}\right)_{2}}$
Questions from NTA Abhyas 2022
5. The force of repulsion between two point charges is $F$ , when these are at distance $0.5 \, m$ apart. Now the point charges are replaced by non conducting spheres of radii $5 \, cm$ each having the same charge as that of the respective point charges. The distance between their centres is again kept $0.5m.$ Then the force of repulsion will
Electrostatic Potential and Capacitance
Physics Most Viewed Questions
1. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
2. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
3. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023
