- Tardigrade
- Question
- Physics
- The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220 Nm -1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2 kg when the spring was in natural length, the whole system is given an acceleration veca as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension (in cm ) of the spring. (g=10 m s -2).
Q.
The arrangement shown in figure is at rest. An ideal spring of natural length $l_{0}$ having spring constant $k=220\, Nm ^{-1}$, is connected to block $A$. Blocks $A$ and $B$ are connected by an ideal string passing through a friction less pulley. The mass of each block $A$ and $B$ is equal to $m=2\, kg$ when the spring was in natural length, the whole system is given an acceleration $\vec{a}$ as shown. If coefficient of friction of both surfaces is $\mu=0.25$, then find the maximum extension (in $cm$ ) of the spring. $\left(g=10\, m s ^{-2}\right)$.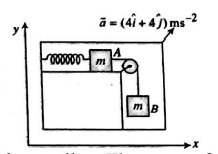
Work, Energy and Power
Report Error
Solution:
Let the maximum extension in spring be $x$.

Apply work-energy theorem: (Net work done by tension will be zero)
$-\frac{1}{2} k x^{2}-8 x-7 x+28 x-2 x=\Delta KE =0$
$\Rightarrow -\frac{1}{2} \times 220 x^{2}+11 x=0$
$\Rightarrow x=0.1\, m =10\, cm$
Questions from Work, Energy and Power
2. Identify the false statement from the following
KEAM 2010
Physics Most Viewed Questions
1. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
2. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
3. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023
