Question

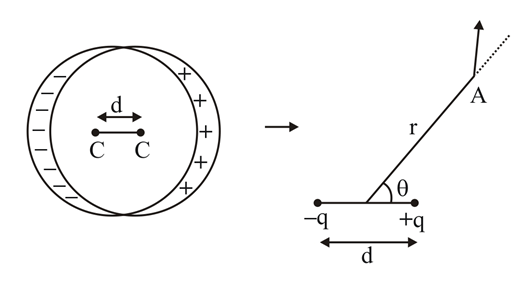
Consider two spheres of the same radius $R$ having uniformly distributed volume charge density of same magnitude but opposite sign $\left(\right.+\rho $ and $-\rho \left..$ The spheres overlap such that the vector joining the centres of the negative sphere to that of the positive sphere is $\overset{ \rightarrow }{d}\left(d \ll R\right).$ The magnitude of the electric field at a point outside the spheres at a distance $r$ in a direction making an angle $\theta $ with $\overset{ \rightarrow }{d}$ is found to be $\frac{\rho }{a \left(\left(\epsilon \right)_{0}\right)}\left(\frac{R^{3} d}{r^{3}}\right)\sqrt{b \left(cos\right)^{2} \theta + 1}.$ The value of $\left(\right.a+b\left.\right)$ is (Distance $r$ is measured with respect to the mid point of the line joining the centers of the two spheres.)

Answer 1

For writing field at an outside point, we can consider the charge on each sphere to be located at respective centre. Thus we have a dipole of dipole moment
$\overset{ \rightarrow }{p}=q\overset{ \rightarrow }{d}$
Where $q=\rho \cdot \frac{4}{3}\pi R^{3}$
Field at $A$
$E=\frac{p}{4 \pi \epsilon _{0} r^{3}}\sqrt{3 cos^{2} \theta + 1}$
$=\frac{\rho }{3 \epsilon _{0}}\frac{R^{3} d}{r^{3}}\sqrt{3 cos^{2} \theta + 1}$