Question

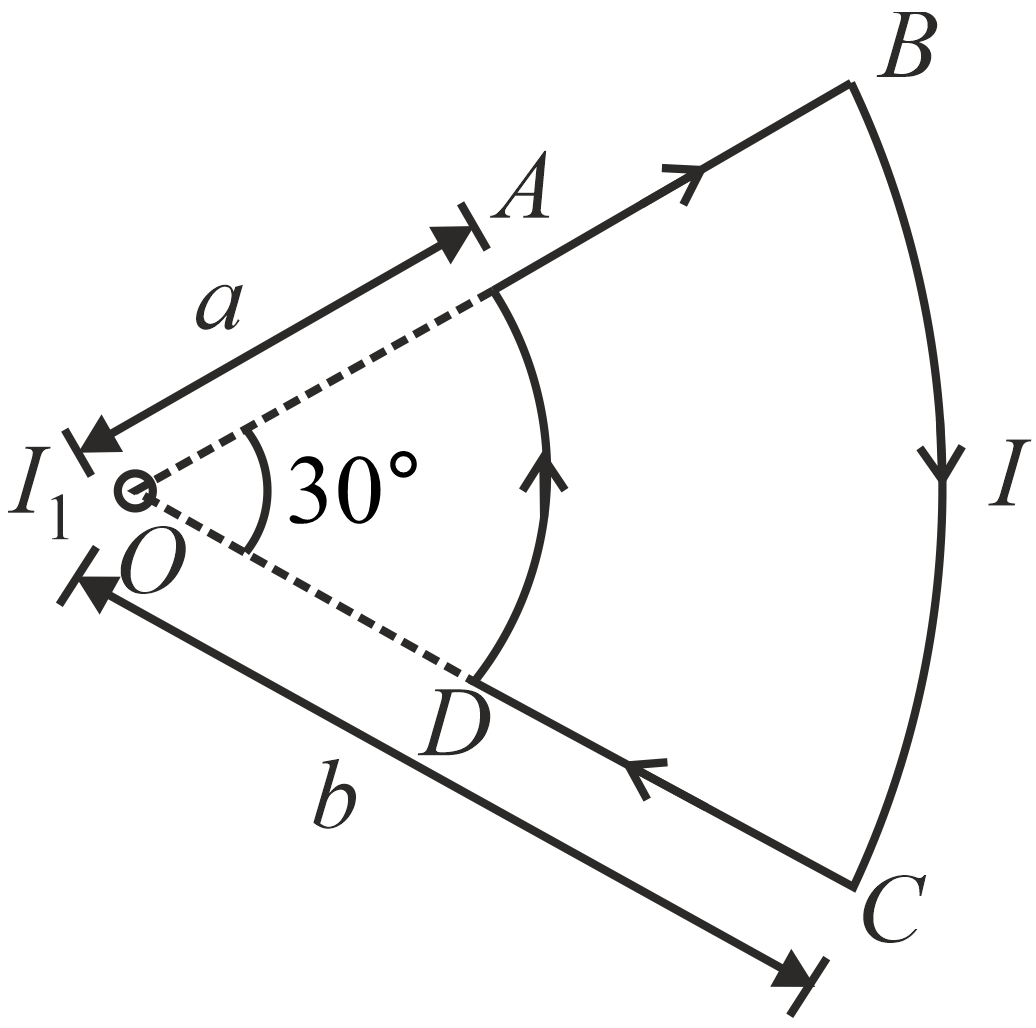
A current loop $ABCD$ is held fixed on the plane of the paper as shown in the figure. The arcs $BC$ (radius = $b$ ) and $DA$ (radius = $a$ ) of the loop are joined by two straight wires $AB$ and $CD$ . A steady current $I$ is flowing in the loop. Angle made by $AB$ and $CD$ at the origin $O$ is $30^\circ $ . Another straight thin wire with steady current $I_{1}$ flowing out of the plane of the paper is kept at the origin.

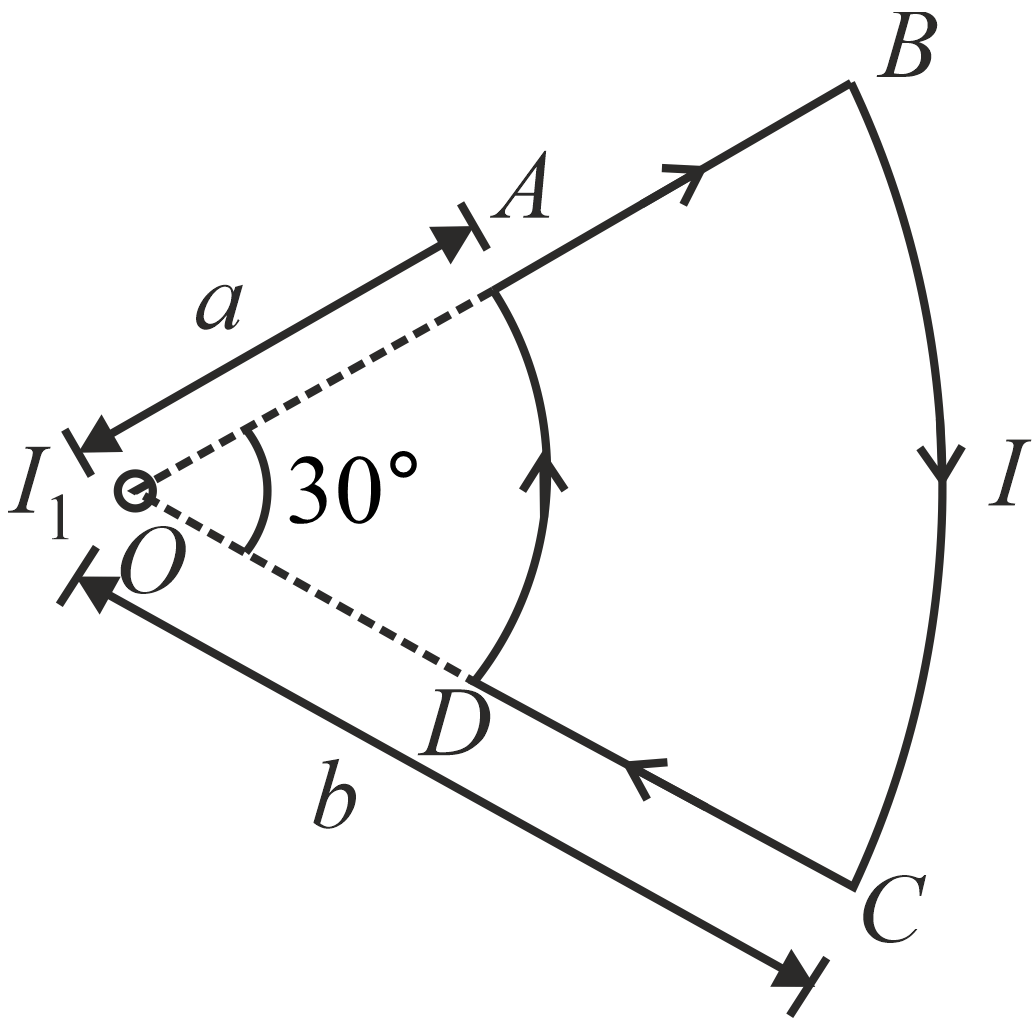
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is

• A. zero
• B. $\frac{\mu_{0} I ( b - a )}{24 a b}$
• C. $\frac{μ_{0} \text{I}}{4 \pi } \left[\frac{\text{b} - \text{a}}{\text{ab}}\right]$
• D. $\frac{\mu_{0} I }{4 \pi}\left[2(b-a)+\frac{\pi}{3}(a+b)\right]$

Answer 1

Answer: (B)

$O$ is along the line $CD$ and $AB$ . They do not contribute to the magnetic induction at $O$ . The field due to $DA$ is positive or out of the paper and that due to $BC$ is into the paper or negative.
The total magnetic field due to loop $ABCD$ at $O$ is $\text{B} = \text{B}_{\text{AB}} + \text{B}_{\text{BC}} + \text{B}_{\text{CD}} + \text{B}_{\text{DA}}$

$\Rightarrow $ $\text{B}=0-\frac{\mu _{0} \text{I}}{4 \pi \text{b}}\times \frac{\pi }{6}+0+\frac{\mu _{0} \text{I}}{4 \pi \text{a}}\times \frac{\pi }{6}$
$\Rightarrow $ $\text{B}=\frac{\left(\mu \right)_{0} \text{I}}{24 \text{ab}}\left(\text{b} - \text{a}\right)$ , out of the paper or positive.