Q. A conducting ring of radius $0.4m$ is placed in a time varrying magnetic field $B=\left(2 + \frac{3 t^{2}}{\pi }\right)$ (where $B$ is in tesla and $t$ is in $s$ ) in such a way that its axis making an angle $60^\circ $ with magnetic field. The emf induced in the ring at $t=2s$ will be
Solution:
$\phi=\overset{ \rightarrow }{B}\cdot \overset{ \rightarrow }{A}$
$=BAcos60^\circ $
$=\left(2 + \frac{3}{\pi } t^{2}\right)\pi \left(\right.0.4\left(\left.\right)^{2}\times \frac{1}{2}$
$=\left(2 + \frac{3}{\pi } t^{2}\right)\pi \times 0.08$
$\left|\right.E\left|\right.=-\left|\frac{d \phi}{d t}\right|$
$E=3\times 0.08\times 2t$
$E=3\times 2\times 2\times 0.08$
$=12\times 0.08$
$=.96V$
Questions from NTA Abhyas 2020
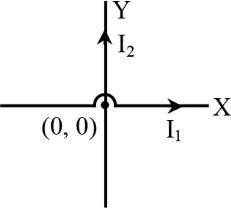
2. Two long straight conductors with current $I_{1}$ and $I_{2}$ are placed along $X$ and $Y$ axes. The equation of locus of point of zero magnetic induction is -
Moving Charges and Magnetism
Physics Most Viewed Questions
1. A car starts from rest and accelerates at $5\, m / s ^{2}$ At $t=4\, s$, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at $t =6\, s$ ? (Take $\left. g =10\, m / s ^{2}\right)$
NEET 2021
Motion in a Straight Line
2. If $E$ and $G$ respectively denote energy and gravitational constant, then $\frac{ E }{ G }$ has the dimensions of:
NEET 2021
Physical World, Units and Measurements
3. The de Broglie wavelength of an electron moving with kinetic energy of $144 \,eV$ is nearly
NEET 2020
Dual Nature of Radiation and Matter
Latest Updates
- JEE Main 2023 February 25th Shift 1 Morning
- JEE Main 2023 February 25th Shift 2 Evening
- JEE Main 2023 January 31st Shift 1 Morning
- JEE Main 2023 January 31st Shift 2 Evening
- JEE Main 2023 January 30th Shift 1 Morning
- JEE Main 2023 January 30th Shift 2 Evening
- JEE Main 2023 January 25th Shift 1 Morning
- JEE Main 2023 January 25th Shift 2 Evening
- JEE Main 2023 January 24th Shift 1 Morning
- JEE Main 2023 January 24th Shift 2 Evening
- JEE Main 2023 February 1st Shift 1 Morning
- JEE Main 2023 February 1st Shift 2 Evening
- JEE Main 2022 July 25th Shift 1 Morning
- JEE Main 2022 July 25th Shift 2 Evening
- JEE Main 2022 July 26th Shift 1 Morning
- JEE Main 2022 July 28th Shift 1 Morning
- JEE Advanced 2022 Paper 2
- JEE Advanced 2022 Paper 1
- JEE Advanced 2021 Paper 2
- JEE Advanced 2021 Paper 1
- JEE Advanced 2020 Paper 2
- JEE Advanced 2020 Paper 1
- NEET 2022 Physics Answer Key
- NEET 2022 Chemistry Answer Key
- NEET 2022 Botany Biology Answer Key
- NEET 2022 Zoology Biology Answer Key
- NEET Rank Predictor 2023
