Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App
NEET 2020 Physics Questions with Answers Key Solutions
Solution:
Bohr model is applicable for only single electron species. Singly ionised neon atom has more than one electron in orbit. Hence, Bohr model is not valid
Solution:
In an electromagnetic wave, half of the intensity is provided by the electric field and half by the magnetic field. Hence, required ratio should be $1 : 1$
Solution:
The brewster angle for any interface should lie between:
$
45< i _{ b }<90 .
$
Solution:
We can express, an ideal gas equation as
$\frac{P}{\rho}=\frac{R.T}{Mw}$
$\Rightarrow \rho=\frac{pMw}{RT}$
$=\frac{249 \times 10^{3}\times 2 \times 10^{-3}}{8.314 \times 300}$
$=0.199$
$\Rightarrow \rho=0.2 kg/m^{3}$
Solution:
Light ray emerges from another surface normally, hence e(angle of emergence) = 0

$\Rightarrow r_{2}=0$
$r_{1}+r_{2}=A$
$\Rightarrow r_{1}=A$
Applying Snell’s law on first surface,
$1. sin\,i=\mu\,sin\,r_{1}$
For small angle , $sin\,\theta\, \approx\,\theta$ Hence,
$i=\mu\,A$
Solution:
The entire system is completely insulated and the free expansion of the gas will take place, the temperature of the gas will remain constant. So the process will be adiabatic.
Solution:
From mass-energy equivalence,
$E=mc^{2}$
$=0.5\times 10^{-3}\times 9\times 10^{16}$
$=4.5 \times 10^{13}\,J$
Solution:
$w_{s}=mg_{s}=72\,N$
$w_{h}=mg_{h}=\frac{mg_{s}}{\left(1+\frac{h}{R}\right)^{2}}$
$=\frac{72\,N}{\left(1+\frac{R /2}{2}\right)}$
$=\frac{72}{9 /4}$
$w_{h}=32\,N$
Solution:
For metals temperature coefficient of resistance is positive while for insulators and semiconductors, temperature coefficient of resistance is negative
Solution:
Displacement of the particle executing SHM $x = A$ sin wt Acceleration of the particle $a =\frac{ d ^2 x }{ dt ^2}$
$
\Longrightarrow a =-A w ^2 \sin w t =A w ^2 \sin (\pi+ wt )
$
Thus phase difference between displacement and acceleration of the particle is $\pi$ radian.
Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App
Solution:
L.C. $=\frac{\text{Pitch}}{\text{Number of division on circular scale}}$
$\Rightarrow 0.01\,mm=\frac{\text{pitch}}{50}$
$\Rightarrow $ pitch $=0.5\,mm$
Solution:
It is given, the difference of $f_{A}$ and $f_{B}$ is $6\,HZ$
Guitar string i.e. string is fixed from both ends

Frequency $\propto \sqrt{\text{Tension}}$
If tension in B slightly decrease then frequency of B decreases
If B is 536 Hz, as the frequency decreases, beats with A also decreases
If B is 524 Hz, as the frequency decreases, beats with A increases
If tension decreases, $f_{B}$ decreases and becomes $f'_{B}$
Now, difference of $f_{A}$ and $f'_{B}=7\,Hz$ (increases)
So, $f_{A}=f_{B}$
$f_{A}-f_{B}=6\,Hz$
$f_{A}=530\,Hz$
$f_{B}=524\,Hz$ (original)
Solution:
Let position of centre of mass be ${(x_{c.m}, 0)}$

$x_{cm}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$
$=\frac{5 \times 0+100 \times 10}{5+10}$
$=\frac{200}{2}$
$=66.66\,cm$
$x_{cm}=67\,cm$
Solution:
Given: $\vec{F}=3 \hat{j}\,N$,
$\vec{r}=2\hat{k}$
We know, $\vec{\tau}=\vec{r}\times\vec{F}=2\hat{k}\times3\hat{j}$
$=6\left(\hat{k} \times\hat{j}\right)=6\left(-\hat{i}\right)$
$\vec{\tau}=-6 \hat{i}\,Nm$
Solution:
Energy received = Intensity $\times$ Area $\times$ Time
$I=\frac{E}{A}$
$E=IAt$
$=\frac{20}{10^{-4}}\times 20\times 10^{-4}\times 60$
$=24 \times 10^{3}\,J$
Solution:
Electric field outside a conducting sphere
$E=\frac{1}{4\pi\varepsilon_{0}} \frac{Q}{r^{2}}$
$=\frac{9\times10^{9}\times3.2\times10^{-7}}{225\times10^{-4}}$
$=0.128\times10^{6}$
$=1.28\times10^{5} N /C$
Solution:
Since electric potential is found throughout constant, hence electric field,
$E=-\frac{dV}{dt}=0$
Solution:
In reverse bias, external battery attracts majority charge carriers
So, width of the depletion region increases
Solution:
The rms value of the current
$i_{\text{rms}}=C\,\omega\,\varepsilon_{\text{rms}}$
$C=40\times10^{-6}F $
$\omega=2\pi\,f =100\,\pi$
$\varepsilon_{\text{rms}}=200\,V $
$\therefore i_{\text{rms}}=200\times40\times10^{-6}\times2\pi\times50$
$=2.5\,A$
Solution:
Mean free path for a gas sample $\lambda_{m}=\frac{1}{\sqrt{2}\pi d^{2} n}$
where d is diameter of a gas molecule and n is molecular density
Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App
Solution:

For Bi-polar junction transistor,
Length profile is $L_{C}>\,L_{E}>\,L_{B}$
and doping profile is $E>\,C>\,B$
Solution:
$K_{1}=1.5 \,hv_{0}-\phi_{0}=0.5\,hv_{0}$
$K_{2}=\frac{1.5}{2}hv_{0}-hv_{0}=-0.25\,hv_{0}$
$\because$ Kinetic energy can never be negative, so no emission and $i=0$
Solution:
$^{235}_{92}U + ^{1}_{0}n \rightarrow ^{89}_{36}Kr+3 ^{1}_{0}n+X_{X}^{A}$
$92+0=36+Z$
$\Rightarrow Z=56$
$235+1=89+3+A$
$\Rightarrow A=144$
So, $^{144}_{56}Ba$ is generated
Solution:
$1\,eV=1.6\times 10^{-19}\\,J$
$1\,J=\frac{1}{1.6\times 10^{-19}}eV$
$10^{-20}\,J=\frac{10^{-20}}{1.6\times 10^{-19}}eV$
$=0.06\,eV$
Solution:
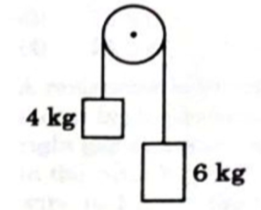
The acceleration of the system $a=\frac{\left(m_{2}-m_{1}\right)g}{m_{1}+m_{2}}$ where $m_{2}>\,m_{1}$
$a=\frac{(6-4)g}{6+4}$
$=\frac{2g}{10}$
$a=\frac{g}{5}$
Solution:
When the new mas is hanged to the wire, the force exerted on the wire is:
$F = mg$
The initial length of the wire is $L$ and the new length is $L_{1}$.
We know that the Young's modulus is given as:
$Y =\frac{ FL _{ o }}{ A \Delta l }$
Here, $L_{o}$ is the initiallength of wire and $\Delta l$ is the chnage in length of wire.
Substitute the values:
$Y =\frac{ mg \times L }{ A \times\left( L _{1}- L \right)}$
So, $Y=\frac{m g L}{A\left(L_{1}-L\right)}$
Solution:
Average thermal energy $=\frac{3}{2}K_{B}T$
(where 3 is translational degree of freedom)
For monoatomic gas total degree of freedom
$f= 3$ (translational degree of freedom)
Solution:
For some metals like copper, resistivity is nearly proportional to temperature although a non linear region always exists at very low temperature
Solution:
From colour coding information for electric resistances, we have
$\begin{matrix}{\text{Yellow}}&{\text{Violet}}&{\text{Brown}}&{\text{Gold}}\\ 4&7&1&5\%\end{matrix}$
So, $R=47 \times 10^{1} \pm\,5\%$
$R=470\,\Omega\,\pm\,5\%$
Solution:
Fringe width, $\beta=\frac{\lambda\,D}{d}$
$\beta' = \frac{\lambda\,D'}{d'}$
Now, $d'=\frac{d}{2}$ and
$D'=2\,D$
So, $\beta'=\frac{\lambda \times 2 D}{d / 2}$
$=\frac{4 \,\lambda\,D}{d}$
$\beta'=4\,\beta$
Fringe width becomes 4 times
Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App
Solution:
$C=KC_{0}$
$K=\frac{C}{C_{0}}$
$=\frac{30}{6}=5$
$K=\frac{\varepsilon}{\varepsilon_{0}}$
$\varepsilon=K\,\varepsilon_{0}$
$=5 \times 8.85\times 10^{-12}$
$=0.44 \times 10^{-10}\,C^{2}\,N^{-1}\,m^{-2}$
Solution:
We know that the formula for the stress is:
$
\text { stress }=\frac{\text { F orce }}{\text { Area }}
$
$
=\frac{\left[ MLT ^{-2}\right]}{\left[ L ^{2}\right]}
$
$
=\left[ ML ^{-1} T ^{-2}\right]
$
Solution:
Limit of resolution,
$\theta_{R}=1.22 \frac{\lambda}{d}$;
$\lambda=600 \times 10^{-9}\,m$
$d=2\,m$
$\theta_{R}=\frac{1.22 \times 600 \times 10^{-9}}{2}$
$\theta_{R}=3.66 \times 10^{-7}$ rad
Solution:
When L is removed,
$tan\,\phi=\frac{\left|X_{C}\right|}{R}$
$\Rightarrow tan \frac{\pi}{3}=\frac{X_{c}}{R} \ldots\left(i\right)$
When C is removed,
$tan \,\phi=\frac{\left|X_{L}\right|}{R}$
$\Rightarrow tan \frac{\pi}{3}=\frac{X_{L}}{R} \ldots\left(ii\right)$
From $\left(i\right)$ and $\left(ii\right)$,
Since $X_{L}=X_{C}$, the circuit is in resonance
$Z=R$
Power factor $=cos\,\phi=\frac{R}{Z}=1$
Solution:
The electric potential due to the dipole,
$V=\frac{kp\,cos\,theta}{r^{2}}$
$=\frac{9\times 10^{9}\times 16\times 10^{-9}}{(0.6)^{2}}\times \frac{1}{2}$
$V=200\,V$
Solution:
Given, $\chi_{m}=599$
Also, $\mu_{r}=1+\chi_{m}=600$
We know, $\mu=\mu_{r}\mu_{o}$
$\mu=600\times4\pi\times10^{-7}$
$\mu=2400\pi\times10^{-7}$
$\mu=2.4\pi\times10^{-4}\,T\,m\,A^{-1}$
Solution:
Magnetic field at centre of solenoid $=\mu_{0}nI$
$n=\frac{N}{L}$
$=\frac{100}{50 \times 10^{-2}}$
$=200$ tums/m
$I = 2.5 \,A$
On putting the values,
$B=4\pi\times 10^{-7}\times 200 \times 2.5$
$=6.28 \times 10^{-4}\,T$
Solution:
Mobility, $\mu =\frac{v_{d}}{E}$
$=\frac{7.5 \times 10^{-4}}{3 \times 10^{-10}}$
$=2.5 \times 10^{6}$
Solution:
Heat supplied $\Delta\,Q =MS\,\Delta\,T$
For same material ‘s’ remains the same
$\Delta\,Q \propto\,M$ and $M=\frac{4}{3}\pi\,r^{3}\,\rho$
$\Rightarrow \frac{\Delta\,Q_{1}}{\Delta\,Q_{2}}$
$=\left(\frac{r_{1}}{r_{2}}\right)^{3}$
$=\left(\frac{1.5}{1}\right)^{3}$
$=\frac{27}{8}$
Solution:
$\lambda = 1.227 \times 10^{-2}\,m$
$=0.1227 \, \mathring{A}$
$\lambda=\frac{12.27}{\sqrt{V}} \mathring{A}$
$0.1227 = \frac{12.27}{\sqrt{V}} \mathring{A}$
$\sqrt{V}\times10^{2} $
$\Rightarrow V=10^{4}$
Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App
Solution:
$9.99 m -0.0099 m =9.9801 m$
But our answer, Should have same no. of significant figures, as the least accurate number.
$\therefore $ Ans $=9.98 m$.
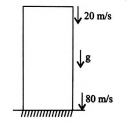
Solution:
Using, $v^{2}=u^{2}+2gh$
Given, $V=80m/s$ and $u=20 m/s$
$h=\frac{v^{2}-u^{2}}{2g}$
$=\frac{6400-400}{20}$
$=300\,m$
Solution:
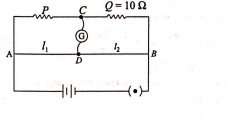
Initially, $\frac{P}{10}=\frac{l_{1}}{l_{2}}=\frac{3}{2}$
$\Rightarrow P=\frac{30}{2}=15\Omega$
Now resistance, $R=\frac{\rho\,l}{A}$
$\frac{R_{1}}{R_{2}}=\frac{l_{1}}{l_{2}}$: Length of $15\,\Omega$ resistance wire is 1.5 m
$\Rightarrow \frac{15}{1}=\frac{1.5}{l_{2}}$
$\Rightarrow l_{2}=0.1\,m$
$=1.0 \times 10^{-1}\,m$
$\therefore $ Length of $1\,\Omega$ resistance wire is $1.0\times 10^{-1}\,m$
Solution:
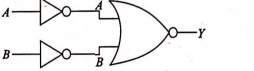
$Y=\overline{\bar{A}+\bar{B}}=\bar{\bar{A}}.\bar{\bar{B}}=A.B$ =AND gate
$\begin{matrix}A&B&Y\\ 0&0&0\\ 0&1&0\\ 1&0&0\\ 1&1&1\end{matrix}$
Download our FREE NEET & JEE Prep App!!
Get Android App
Get iOS App