JEE Main Question Paper with Solution 2023 January 29th Shift 2 - Evening

A

$3.38 \times 10^{24}$

B

$6.76 \times 10^{24}$

C

$6.76 \times 10^{23}$

D

$1.69 \times 10^{24}$

Solution

$ \left( N _0\right) A =\frac{320}{16}=20 \text { moles } $
$ \left( N _0\right) B =\frac{320}{32}=10 \text { moles } $
$ N _{ A }=\frac{\left( N _0\right)_{ A }}{(2)^{2 / 1}}=\frac{20}{4}=5 $
$N _{ B }=\frac{\left( N _0\right)_{ B }}{(2)^{2 / 5}}=\frac{10}{2^4}=0.625$
$ \text { Total } N =5.625 $
$ \text { No. of atoms }=5.625 \times 6.023 \times 10^{23}$
$=3.38 \times 10^{24}$

A

32

B

28

C

24

D

27

Solution

$ \sqrt{\frac{3 RT }{ M }}=\sqrt{\frac{\alpha+5}{\alpha}} \sqrt{\frac{8}{\pi} \frac{ RT }{ M }} $
$3=\frac{\alpha+5}{\alpha} \frac{8}{\pi} $
$ \alpha=28$

A

4

B

16

C

8

D

2

Solution

$\frac{\lambda_{\alpha}}{\lambda_{p}}=\frac{h}{\sqrt{\frac{2m_{\alpha}q_{\alpha}V}{\frac{h}{\sqrt{2m_{p}q_{p}V}}}}}$
$\frac{\lambda_\alpha}{\lambda_p}=\sqrt{\frac{1}{8}} \,\,\,\, m =8$

A

B

C

D

A

$\sqrt{\frac{1}{1- n ^2}}$

B

$\sqrt{1-\frac{1}{n^2}}$

C

$1+\frac{1}{n^2}$

D

$1-\frac{1}{n^2}$

Solution

$ a _1= g \sin \theta= g / \sqrt{2} $
$ a _2= g \sin \theta- Kg \cos \theta=\frac{ g }{\sqrt{2}}-\frac{ Kg }{\sqrt{2}} $
$ t _2= nt _1 \,\, \& \,\,\, a _1 t _1^2= a _2 t _2^2 $
$ \frac{ g }{\sqrt{2}} t _1^2=\left(\frac{ g }{\sqrt{2}}-\frac{ kg }{\sqrt{2}}\right) n ^2 t _1^2$
$ K =1-\frac{1}{ n ^2} $

A

40 N

B

5 N

C

20 N

D

10 N

Solution

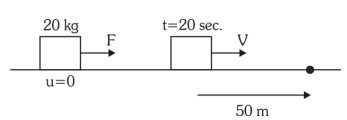
$ 50=V \times 10$
$V=5 \,m / s $
$ V =0+ a \times 20$
$ 5= a \times 20 $
$ a =\frac{1}{4} \,m / s ^2 $
$ F = ma =20 \times \frac{1}{4}=5 N $

A

16

B

6

C

8

D

10

Solution

$ P _2 A - P _1 A =5.4 \times 10^5 \times g $
$ P_2-P_1=\frac{5.4 \times 10^6}{500}=5.4 \times 2 \times 10^2 \times 10 $
$=10.8 \times 10^3 $
$ P _2+0+\frac{1}{2} \rho V _2^2= P _1+0+\frac{1}{2} \rho V _1^2$
$P _2- P _1=\frac{1}{2} \rho\left( V _1^2- V _2^2\right)=\frac{1}{2} \rho\left( V _1- V _2\right)\left( V _1+ V _2\right)$
$10.8 \times 10^3=\frac{1}{2} \times 1.2\left( V _1- V _2\right) \times 2 \times 3 \times 10^2 $
$ 10.8 \times 10=3.6\left( V _1- V _2\right) $
$ V _1- V _2=30 $
$ \left(\frac{ V _1- V _2}{ V }\right) \times 100=\frac{30}{300} \times 100=10 \%$

A

B and E only

B

A and C only

C

B, D and E only

D

B and D only

A

$v =4 \hat{ i } \,m / s , a =8 \hat{ j }\, m / s ^2$

B

$v =4 \hat{ j } \,m / s , a =8 \hat{ i }\, m / s ^2$

C

$v =-4 \hat{ j } \,m / s , a =8 \hat{ i } \,m / s ^2$

D

$v =-4 \hat{i} \,m / s , a =-8 \hat{ j } \,m / s ^2$

Solution

$ a _{ c }=\frac{ V ^2}{ r }=\frac{4^2}{2}=\frac{16}{2}=8\,m / s ^2 $
$\vec{ V }=4 \hat{ j } $
$ \vec{a_c}=8 \hat{ i }$

A

$1200 \,mJ$

B

$600\, mJ$

C

$-600\, mJ$

D

$-1200 \,mJ$

Solution

$ \omega_{ E }= q \vec{ E } \cdot \vec{ S }$
$ =2 \times 10^{-2}[30 \hat{ i } \cdot(-\hat{ i })] $
$=2 \times 10^{-2}(-30) $
$=-60 \times 10^{-2} $
$=-\frac{60}{100}=-0.6\, J $
$ =-600 \,mJ$

A

1.4

B

0.4

C

0.2

D

0.6

Solution

$ \mu=\text { modulation index }=\frac{A_{\max }-A_{\min }}{A_{\max }+A_{\min }} $
$ =\frac{14-6}{14+6}=0.4$

A

8T

B

4T

C

2T

D

16T

Solution

$ B =\frac{\mu_0 i }{2 R } \times 4 $
$ B ^{\prime} =\frac{\mu_0 i }{2 R ^{\prime}} $
$R ^{\prime} =4 R$
$ B ^{\prime} =\frac{\mu_0 i }{8 R } $
$ \frac{ B ^{\prime}}{ B } =\frac{1}{16} $
$ B ^{\prime} =2 T $

A

B and D only

B

A and C only

C

A only

D

C only

Solution

Sensitivity of potentiometer wire is inversely proportional to potential gradient.

A

Increase the wave length of the light

B

Increase the refractive index of the medium between the object and objective lens

C

Decrease the focal length of the eye piece

D

Decrease the diameter of the objective lens

Solution

$P=\frac{2 \mu \sin \theta}{1.22 \lambda}$

A

Statement I is true but statement II is false

B

Both Statement I and Statement II are true

C

Statement I is false but statement II is true

D

Both Statement I and Statement II are false

Solution

Statement-I is correct as EMW are neutral.
Statement-II is wrong.
$E _0=\sqrt{\frac{1}{\mu_0 \varepsilon_0}} B_0$

A

A and D only

B

B and D only

C

A and E only

D

A and C only

Solution

$ \Delta Q =184 \times 10^3$
$ m =0.600 \,kg \, \text { at }-12^{\circ} C $
$ S =222.3 \, J / kg /{ }^{\circ} C $
$ L =336 \times 10^3 J / kg $
$ Q _1=0.600 \times 2222.3 \times 12=16000.56 \, J$
Remaining heat $\Delta Q_1=184000-16000.56$
$=167999.44 \, J$
For meeting at $0^{\circ} C$
$\Delta Q_2=0.600 \times 336000=201600 J$ needed
$\therefore 100 \%$ ice is not melted
Amount of ice melted
$167999.44= m \times 336000=0.4999 \,kg$
$\therefore$ mass of water $=0.4999 \, kg$
Mass of ice $=0.1001$
$\therefore \text { Ratio }=\frac{0.1001}{0.4999} \approx 1: 5$

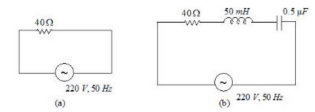
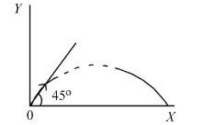
A

The rms current in circuit (b) can never be larger than that in (a)

B

The rms current in figure (a) is always equal to that in figure (b)

C

The rms current in circuit (b) can be larger than that in (a)

D

At resonance, current in (b) is less than that in (a)

Solution

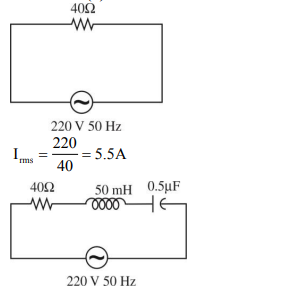
$X _{ L }$ is not equal to $X _{ C }$. So rms current in (b) can never be larger than (a).

A

4 hours

B

6 hours

C

12 hours

D

3 hours

Solution

$ T ^2 \propto R ^3$
$ \frac{ T _1^2}{ T _2^2}=\frac{ R _1^3}{ R _2^3} \Rightarrow\left(\frac{ T _1}{ T _2}\right)^2=\left(\frac{ R }{\frac{ R }{4}}\right)^3$
$\therefore \frac{ T _1^2}{ T _2^2}=64 $
$\therefore T _2^2=\frac{ T _1^2}{64}$
$\therefore T _2=\frac{24}{8}=3$

A

$A =\left[ L ^{-1} T \right], B =\left[ LT ^{-1}\right]$

B

$A =( LT ], B =\left[ L ^{-1} T ^{-1}\right]$

C

$A =\left[ L ^{-1} T ^{-1}\right], B =\left[ LT ^{-1}\right]$

D

$A =\left[ L ^{-1} T ^{-1}\right], B =[ LT ]$

Solution

$ ( x - At )^2+\left( y -\frac{ t }{ B }\right)^2= a ^2$
$ {[ At ]= A \times \frac{1}{ T }= L }$
$ \therefore [ A ]= T ^1 L ^1 $
$ \frac{ t }{ B } $ is in meters
$ \therefore \frac{1}{ T [ B ]}= L ^2$
$ \therefore [ B ]= T ^{-1} L ^{-1}$

A

$2.5 \times 10^{-3} J$

B

$1.0 \times 10^{-3} J$

C

$1.0 \times 10^{-4} J$

D

$5 \times 10^{-3} J$

Solution

Sol. $\ell=50\, cm$
$ t =1 \sec$
$\therefore V =\frac{0.05}{1}=0.05\, m / s . $
$ i =\frac{40 \times 0.05 \times 0.05}{10}=0.01 A$
$\therefore F = B _{ i } \ell=40 \times 0.01 \times 0.05$
$F =0.02 \,N $
$\therefore W =0.02 \times \ell=0.02 \times .05 $
$\therefore W =1 \times 10^{-3} J$

Solution

$\frac{ R _1+ R _2}{10}=\frac{60}{40}=\frac{3}{2} $
$\Rightarrow R _1+ R _2=15$
Now $\frac{R_1 R_2}{\left(R_1+R_2\right) \times 3}=\frac{40}{60}=\frac{2}{3} $
$\Rightarrow R_1 R_2=30$

Solution

Use $\Delta L =\int\limits_0^t \tau d t$
$ L _0=\int\limits_0^2 mg \left( v _{ x } t \right) dt $
$ = mgv _{ x } \frac{ t ^2}{2}=(0.1)(10)(10 \sqrt{2}) \frac{2^2}{2} $
$ =20 \sqrt{2} $
$ =\sqrt{800}\, kg\, m ^2 / s$

Solution

$u =\frac{ h }{ h ^{\prime}}=\frac{5.25}{5.00}$
Least count $=\frac{1}{20} cm -\frac{49}{50} \cdot \frac{1}{20} cm$
$=\frac{1}{50} \times \frac{1}{20} \,cm =0.01 \,mm$
$\ln u =\ln h -\ln h ^{\prime}$
$\frac{ du }{ u }=\frac{ dh }{ h }-\frac{ dh { }^{\prime}}{ h ^{\prime}}$
$du =\left[\frac{0.01}{5.25}+\frac{0.01}{5.00}\right] \frac{5.25}{5.00}$
$=\frac{41}{10} \times 10^{-3}$
$=41$

Solution

$E =-\frac{ dV }{ dr }=-4 ar \equiv \frac{\rho r }{3 \varepsilon_0} $ (compare)
Result inside uniformly charged solid sphere.
$\rho=-12 a \varepsilon_0$
$\lambda=12$

Solution

$ v \frac{d v}{d x}=\frac{v^2}{R} $ $\Rightarrow \int\limits_{15}^v \frac{d v}{v}=\frac{1}{R} \int\limits_0^x d x $
$ v=15 \,e^{x / R} $
$ \frac{d x}{d t}=15\, e^{x / R}$
$ \int\limits_0^ \frac{\pi R}{2} e^{-x / R} d x=15 \int\limits_0^{t_0} d t $
$ t_0=40\left(1-e^{-\pi / 2}\right)$

Solution

$\frac{1}{2 \pi fC }=2 \pi fL$
$ C =\frac{1}{4 \pi^2 f ^2 L }=\frac{1}{4 \times \pi^2 \times 49 \times 10^6 \times 2 \times 10^{-6}} $
$ C =\frac{1}{3872} F $
$ x =3872$

Solution

$| F |=\eta A \frac{\Delta v }{\Delta h }: 0.1$
$=5 \times 10^{-3} \times 0.2 \times \frac{ v }{.25 \times 10^{-3}} $
$ v =0.025\, m / s$
or $ v =25 \times 10^{-3} \,m / s$

Solution

$\frac{1}{4} a =-25 x ; a =-100 x $
$ \omega^2=100 \,\,\,\,\omega=10 $
$ \omega A =4 $
$ A =\frac{4}{10}=0.4 \,m $
$ A =40 \,cm $

Solution

$ \mu_1=\sqrt{2.8 \times 1}=\sqrt{2.8}$
$\mu_2=\sqrt{6.8 \times 1}=\sqrt{6.8} $
$ \mu_1 \sin i=\mu_2 \cos i $
$\tan i=\frac{\mu_2}{\mu_1}=\sqrt{\frac{6.8}{2.8}} $
$ \tan i =\left(\frac{2.8+4}{2.8}\right)^{1 / 2} $
$i=\tan ^{-1}\left(1+\frac{10}{7}\right)^{1 / 2} $
$ \theta=7 $

Solution

$ \frac{\varepsilon}{ r +5} \times 5=200\, x $.....(1)
$ \frac{\varepsilon \times 15}{ r +15}=300\, x $....(2)
$ \Rightarrow r =5 \,\Omega$

A

Statement I is incorrect but statement II is correct.

B

Both the statements I and II are correct

C

Statement I is correct but statement II is incorrect

D

Both the statements I and II are incorrect

Solution

The first ionization energies (as in NCERT) are as
follows:
$B : 801 \,kJ/mol $
$Al : 577\, kJ/mol $
$Ga : 579\, kJ/mol $
$Ga :[ Ar ] \,3 d ^{10} \,4 s ^2\, 4 p ^1$

A

$\left[ FeF _6\right]^{3-} >\left[ CoF _6\right]^{3-} >\left[ Co \left( C _2 O _4\right)_3\right]^{3-}$

B

$\left[ Co \left( C _2 O _4\right)_3\right]^{3-} >\left[ CoF _6\right]^{3-} >\left[ FeF _6\right]^{3-}$

C

$\left[ FeF _6\right]^{3-} >\left[ Co \left( C _2 O _4\right)_3\right]^{3-} >\left[ CoF _6\right]^{3-}$

D

$\left[ CoF _6\right]^{3-} >\left[ FeF _6\right]^{3-} >\left[ Co \left( C _2 O _4\right)_3\right]^{3-}$

Solution

A

A-I, B-III, C-IV, D-II

B

A-III, B-I, C-IV, D-II

C

A-III, B-I, C-II, D-IV

D

A-I, B-III, C-II, D-IV

Solution

A. Osmosis III
B. Reverse osmosis I
C. Electro osmosis IV
D. Electrophoresis II

A

(ii) and (iii)

B

(i), (ii) and (iv)

C

(i) and (iii)

D

(ii), (iii) and (iv)

Solution

(i), (ii) and (iv) correct.
Manganese exhibits $+7$ oxidation state in its oxide. $\left( Mn _2 O _7\right)$
$Ru \,\&\,Os$ from $RuO _4\, \& \,OsO _4$ oxide in $+8$ oxidation state
$Cr$ in $+6$ oxidation act is oxidizing.
$Sc$ does not show $+4$ oxidation state.

A

A-II, B-III, C-I, D-IV

B

A-II, B-I, C-IV, D-III

C

A-IV, B-III, C-I, D-II

D

A-IV, B-I, C-III, D-II

Solution

Neoprene : Elastomer
Polyester : Fibre
Polystyrene : Thermoplastic
Urea-Formaldhyde Resin: Thermosetting polymer

A

Starch and iodine

B

Methyl orange and $H _2 O _2$

C

Starch and $H _2 O _2$

D

Methyl orange and iodine

Solution

$I ^{-}+ H _2 O _2 \longrightarrow \underset{(A)}{I _2}+ H _2 O$
$I _2+\underset{\text { (Indicator) }}{\text { Starch }} \longrightarrow \text { Blue }$

A

Stomach ulcers

B

Hyperacidity

C

Anxiety and stress

D

Depression and hypertension

A

B

C

D

A

1-Bromo-2-methylbutane

B

2-Bromopropane

C

2-Bromopentane

D

2-Bromo-3,3-dimethylpentane

A

$C _8 H _6$

B

$C _9 H _9$

C

$C _6 H _6$

D

$C _9 H _6$

Solution

$C _{ x } H _{ y }+\left( x +\frac{ y }{4}\right) O _2 \rightarrow xCO _2+\frac{ y }{2} H _2 O$
$ x +\frac{ y }{4}=9.5 $
$ \frac{ y }{2}=3 $
$ \Rightarrow x =8, y =6$

A

B

C

D

A

1,3 and 3

B

1, 3 and 2

C

1,2 and 3

D

2,3 and 3

A

Green

B

Orange-Red

C

Yellow

D

Blue

Solution

A solution of $CrO_5$ in amyl alcohol has a blue colour.

A

X = 6 ,Y= 5

B

X =4 ,Y=8

C

X =4 ,Y=15

D

X =6 ,Y=12

Solution

The growth of fish gets inhibited if the concentration of dissolved Oxygen in water is less than $6$ ppm and Biochemical Oxygen demand in clean water should be less than $5$ ppm

A

Ethylnitrile

B

Propylamine

C

Propanenitrile

D

Ethylamine

A

FIQY

B

FLDY

C

YQLF

D

PLDY

Solution

Hydrolysis of the given tetrapeptide will give the following:

A

C and D only

B

B and C only

C

A and B only

D

B and D only

Solution

Only (B) and (C) are correct.
(B) $G = H - TS$
At constant $T$
$\Delta G =\Delta H - T \Delta S$
(A) First law is given by
$\Delta U = Q + W$
If we apply constant $P$ and reversible work.
$\Delta U = Q - P \Delta V$
(C)By definition of entropy changc
$dS =\frac{ dq _\text{ rev }}{ T }$
At constant $T$
$\Delta S =\frac{ q _\text{ rev }}{ T }$
(D) $H = U + PV$
For ideal gas
$H = U + nRT$
At constant $T$
$\Delta H =\Delta U +\Delta nRT$

A

Calamine

B

Siderite

C

Sphalerite

D

Malachite

Solution

Calamine: $ZnCO _3$
Siderite : $FeCO _3$
Sphalerite : $ZnS$
Malachite : $CuCO _3 \cdot Cu ( OH )_2$

A

Both the statements I and II are correct

B

Statement I is incorrect but statement II is correct

C

Both the statements I and II are incorrect

D

Statement I is correct but statement II is incorrect

Solution

Statement-I is correct.
$Ni$ is used in Hydrogenation of unsaturated fat to make edible fats.
Statements-II is false as hydride of Silicon is electron precise & neither electron deficient nor electron rich.

A

A-III, B-I, C-II, D-IV

B

A-III, B-II, C-I, D-IV

C

A-III, B-I, C-IV, D-II

D

A-I, B-III, C-II, D-IV

Solution

(A) van't Hoff factor, $i$
$i =\frac{\text { Normal molar mass }}{\text { Abnormal molar mass }}$
(B) $k _{ f }=$ Cryoscopic constant
(C) Solutions with same osmotic pressure are known as isotonic solutions.
(D) Solutions with same composition of vapour over them are called Azeotrope.

Solution

$2 Li NO _3 \xrightarrow{\Delta}Li _2 O +2 NO _2+\frac{1}{2} O _2$
Hence three products $Li _2 O , NO _2$ and $O _2$

Solution

$ N _2( g )+3 H _2( g ) \rightleftharpoons 2 NH _3( g ), K _1=4 \times 10^5 \ldots( i )$
$ N _2( g )+ O _2( g ) \rightleftharpoons 2 NO ( g ), K _2=1.6 \times 10^{12} \ldots( ii )$
$ H _2( g )+\frac{1}{2} O _2( g ) \rightleftharpoons H _2 O ( g ), K _3=1.0 \times 10^{-13} \ldots (iii)$
$(ii)+3 \times( iii)-( i)$
$ 2 NH _3( g )+\frac{5}{2} O _2( g ) \rightleftharpoons 2 NO ( g )+3 H _2 O ( g )$
$k _{ eq }=\frac{ k _2 \times k _3^3}{ k _1}=\frac{1.6 \times 10^{12} \times\left(10^{-13}\right)^3}{4 \times 10^5} $
$ =\frac{1.6}{4} \times 10^{-32}=4 \times 10^{-33}$

Solution

As unit of rate constant is (conc. $)^{1-n}$ time $^{-1}$
$ \Rightarrow\left( L \,mol ^{-1}\right) \Rightarrow 1- n =-1 $
$ n =2 $

Solution

Acidic oxides are $N _2 O _3, NO _2, Cl _2 O _7, SO _2$

Solution

Let $M$ is the molar mass of the compound $( g / mol )$
mass of compound $=0.01 \,Mgm$
mass of carbon $=0.01 M \times \frac{60}{100}$
moles of carbon $=\frac{0.01 M }{12} \times \frac{60}{100}$
moles of $CO _2$ from combustion $=\frac{4.4}{44}=$ moles of carbon
$\frac{0.01 M }{12} \times \frac{60}{100}=\frac{4.4}{44}$
$M =\frac{4.4}{44} \times \frac{100}{60} \times \frac{12}{0.01}=200\, gm / mol$

Solution

One unit cell of hep contains $=18$ voids
No. of voids in $0.02 \,mol$ of hcp
$ =\frac{18}{6} \times 6.02 \times 10^{23} \times 0.02 $
$ \approx 3.6 \times 10^{22} $
$\approx 36 \times 10^{21}$

Solution

$ r \propto \frac{ n ^2}{ Z }$
$ r _{ He ^{+}} = r _{ H } \times \frac{ n ^2}{ Z } $
$ r _{ He ^{+}} =0.6 \times \frac{(3)^2}{2} $
$ =2.7 \mathring{A} $
$r _{ He ^{+}} =270 \,pm$

Solution

$ Zn ( s )+ Sn ^{2+}( aq ) \rightleftharpoons Zn ^{2+}( aq )+ Sn ( s ) $
$ \Delta G ^{\circ}=-2.303 RT \log _{10} Keq $
$ - nF \left( E _\text{ cell }^0\right)=-2.303 RT \log _{10} Keq $
$ E _{ Zn / Zn ^{2+}}^0+ E _{ Sn ^{2+} / Sn }^0=\frac{0.059}{2} \log _{10} Keq $
$ 0.76+ E _{ Sn ^{2+} / Sn }^0=\frac{0.059}{2} \log _{10} 10^{20} $
$ 0.76+ E _{ Sn ^{2+} / Sn }^0=\frac{0.059 \times 20}{2} $
$ E _{ Sn ^{2+} / Sn ^0}=0.59-0.76=-0.17 $
$ E _{ Sn / Sn ^{2+}}^0=17 \times 10^{-2} V $
$ =17$

Solution

Mole of $Na =\frac{0.69}{23}=3 \times 10^{-2}$
$Na + H _2 O \longrightarrow NaOH +\frac{1}{2} H _2$
By using POAC
Moles of $NaOH =3 \times 10^{-2}$
$NaOH$ reacts with $HCl$
No. of equivalent of $NaOH = No$. of equivalent of $HCl$
$3 \times 10^{-2} \times 1=\frac{73}{36.5} \times V (\text { in } L ) \times 1$
$V =1.5 \times 10^{-2} L$
Volume of $HCl =15\, ml$.

A

$B \Rightarrow( A \Rightarrow B )$

B

$A \Rightarrow( A \Leftrightarrow B )$

C

$A \Rightarrow((\sim A ) \Rightarrow B )$

D

$B \Rightarrow((\sim A ) \Rightarrow B )$

Solution

A	B	$\sim A$	$\sim A \vee B$	$B \Rightarrow((\sim A ) \vee B )$
T	T	F	T	T
T	F	F	F	T
F	T	T	T	T
F	F	T	T	T

$A \Rightarrow B$	$\sim A \Rightarrow B$	$B \Rightarrow ( A \Rightarrow B )$	$ A \Rightarrow ((\sim A ) \Rightarrow B )$	$ B \Rightarrow ((\sim A ) \Rightarrow B )$
T	T	T	T	T
F	T	T	T	T
T	T	T	T	T
T	F	T	T	T

A

$2 \sqrt{3}$

B

$4 \sqrt{3}$

C

$3 \sqrt{3}$

D

$5 \sqrt{3}$

Solution

$ \frac{x-1}{2}=\frac{y+8}{-7}=\frac{z-4}{5} \,\,\,\,\vec{ a }=\hat{ i }-8 \hat{ j }+4 \hat{ k } $
$ \frac{ x -1}{2}=\frac{ y -2}{1}=\frac{ z -6}{-3} \,\,\,\,\vec{ b }=\hat{ i }+2 \hat{ j }+6 \hat{ k } $
$ \vec{ p }=2 \hat{ i }-7 \hat{ j }+5 \hat{ k }, \vec{ q }=2 \hat{ i }+\hat{ j }-3 \hat{ k } $
$ \vec{ p } \times \vec{ q }=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 2 & -7 & 5 \\ 2 & 1 & -3\end{vmatrix} $
$ =\hat{ i }(16)-\hat{ j }(-16)+\hat{ k }(16) $
$ =16(\hat{ i }+\hat{ j }+\hat{ k }) $
$ d =\left|\frac{( a - b ) \cdot(\vec{ p } \times \vec{ q })}{|\vec{ p } \times \vec{ q }|}\right|=\left|\frac{(-10 \hat{ j }-2 \hat{ k }) \cdot 16(\hat{ i }+\hat{ j }+\hat{ k }) \mid}{16 \sqrt{3}}\right| $
$=\left|\frac{-12}{\sqrt{3}}\right|=4 \sqrt{3}$

A

34

B

12

C

36

D

30

Solution

$ \vec{ r } \times \vec{ b }-\vec{ c } \times \vec{ b }=0 $
$ \Rightarrow(\vec{ r }-\vec{ c }) \times \vec{ b }=0$
$ \Rightarrow \vec{ r }-\vec{ c }=\lambda \vec{ b }$
$ \Rightarrow \vec{ r }=\vec{ c }+\lambda \vec{ b } $
And given that $\vec{ r } \cdot \vec{ a }=0$
$\Rightarrow(\vec{ c }+\lambda \vec{ b }) \cdot \vec{ a }=0$
$ \Rightarrow \vec{ c } \cdot \vec{ a }+\lambda \vec{ b } \cdot \vec{ a }=0$
$\Rightarrow \lambda=\frac{-\vec{ c } \cdot \vec{ a }}{\vec{ b } \cdot \vec{ a }} $
Now $ \vec{ r } \cdot \vec{ c }=(\vec{ c }+\lambda \vec{ b }) \cdot \vec{ c }$
$ =\left(\vec{ c }-\frac{\vec{ c } \cdot \vec{ a }}{\vec{ b } \cdot \vec{ a }} \vec{ b }\right) \cdot \vec{ c } $
$=|\vec{ c }|-\left(\frac{\vec{ c } \cdot \vec{ a }}{\vec{ b } \cdot \vec{ a }}\right)(\vec{ b } \cdot \vec{ c }) $
$ =74-\left[\frac{15}{3}\right] 8 $
$ =74-40=34$

A

$\frac{3}{32}$

B

$\frac{3}{64}$

C

$\frac{1}{16}$

D

$\frac{1}{32}$

Solution

Let $P \left( w _1\right)=\lambda$ then $P \left( w _2\right)=\frac{\lambda}{2} \ldots P \left( w _{ n }\right)=\frac{\lambda}{2^{ n -1}}$
As $\displaystyle\sum_{ k =1}^{\infty} P \left( w _{ k }\right)=1 \Rightarrow \frac{\lambda}{1-\frac{1}{2}}=1 \Rightarrow \lambda=\frac{1}{2}$
So, $P \left( w _{ n }\right)=\frac{1}{2^{ n }}$
$ A =\{2 k +3 \ell ; k , \ell \in N \}=\{5,7,8,9,10 \ldots . .\} $
$ B =\left\{ w _{ n }: n \in A \right\} $
$ B =\left\{ w _5, w _7, w _8, w _9, w _{10}, w _{11}, \ldots .\right\} $
$ A = N -\{1,2,3,4,6\} $
$ \therefore P ( B )=1-\left[ P \left( w _1\right)+ P \left( w _2\right)+ P \left( w _3\right)+ P \left( w _4\right)+ P \left( w _6\right)\right] $
$ =1-\left[\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{64}\right] $
$=1-\frac{32+16+8+4+1}{64}=\frac{3}{64}$

A

$\tan ^{-1} \frac{1}{2}+\frac{1}{3} \tan ^{-1} 8-\frac{\pi}{3}$

B

$\tan ^{-1} 2-\frac{1}{3} \tan ^{-1} 8+\frac{\pi}{3}$

C

$\tan ^{-1} 2+\frac{1}{3} \tan ^{-1} 8-\frac{\pi}{3}$

D

$\tan ^{-1} \frac{1}{2}-\frac{1}{3} \tan ^{-1} 8+\frac{\pi}{3}$

Solution

$ I =\int\limits_1^2\left(\frac{ t ^4+1}{ t ^6+1}\right) dt $
$ =\int\limits_1^2 \frac{\left( t ^4+1- t ^2\right)+ t ^2}{\left( t ^2+1\right)\left( t ^4- t ^2+1\right)} dt $
$=\int\limits_1^2\left(\frac{1}{ t ^2+1}+\frac{ t ^2}{ t ^6+1}\right) dt $
$=\int\limits_1^2\left(\frac{1}{ t ^2+1}+\frac{1}{3} \frac{3 t ^2}{\left( t ^3\right)^2+1}\right) dt $
$ =\tan ^{-1}(t)+\left.\frac{1}{3} \tan ^{-1}\left(t^3\right)\right|_1 ^2 $
$ =\left(\tan ^{-1}(2)-\tan ^{-1}(1)\right)+\frac{1}{3}\left(\tan ^{-1}\left(2^3\right)-\tan ^{-1}\left(1^3\right)\right) $
$ =\tan ^{-1}(2)+\frac{1}{3} \tan ^{-1}(8)-\frac{\pi}{3}$

A

$(50,51)$

B

$(51,99)$

C

$(50,101)$

D

$(51,101)$

Solution

In the expansion of
$ (1+ x )^{99}= C _0+ C _1 x + C _2 x ^2+\ldots .+ C _{99} x ^{99}$
$ K = C _1+ C _3+\ldots .+ C _{99}=2^{98}$
$a \Rightarrow$ Middle in the expansion of $\left(2+\frac{1}{\sqrt{2}}\right)^{200}$
$T _{\frac{200}{2}+1} ={ }^{200} C _{100}(2)^{100}\left(\frac{1}{\sqrt{2}}\right)^{100} $
$ ={ }^{200} C _{100} \cdot 2^{50}$
So, $\frac{{ }^{200} C _{99} \times 2^{98}}{{ }^{200} C _{100} \times 2^{50}}=\frac{100}{101} \times 2^{48}$
So, $\frac{25}{101} \times 2^{50}=\frac{m}{n} 2^{\ell}$
$\therefore m , n$ are odd so
$(\ell, n )$ become $(50,101)$

A

$g (-2)- f (-2)=20$

B

If $-1< x< 2$, then $|f(x)-g(x)|< 8$

C

$\left|f^{\prime}(x)-g^{\prime}(x)\right|< 6 \Rightarrow-1< x< 1 \mid$

D

There exists $x _0 \in\left(1, \frac{3}{2}\right)$ such that $f \left( x _0\right)= g \left( x _0\right)$

Solution

$ f^{\prime \prime}(x)=g^{\prime \prime}(x)+6 x $....(1)
$ f^{\prime}(1)=4 g^{\prime}(1)-3=9$....(2)
$ f(2)=3 g(2)=12$ ....(3)
By integrating (1)
$f^{\prime}(x)=g^{\prime}(x)+6 \frac{x^2}{2}+C$
At $x =1$,
$ f ^{\prime}(1)= g ^{\prime}(1)+3+ C$
$\Rightarrow 9=4+3+ C \Rightarrow C =3$
$\therefore f ^{\prime}( x )= g ^{\prime}( x )+3 x ^2+3$
Again by integrating,
$f(x)=g(x)+\frac{3 x^3}{3}+3 x+D $
$ \text { At } x=2$
$ f(2)=g(2)+8+3(2)+D $
$ \Rightarrow 12=4+8+6+D \Rightarrow D=-6$
So, $f(x)=g(x)+x^3+3 x-6$
$\Rightarrow f(x)-g(x)=x^3+3 x-6$
At $x=-2$,
$\Rightarrow g (-2)- f (-2)=20 $ (Option (1) is true)
Now, for $-1< x , 2$
$ h(x)=f(x)-g(x)=x^3+3 x-6 $
$ \Rightarrow h^{\prime}(x)=3 x^2+3$
$ \Rightarrow h(x) \uparrow$
So, $h (-1)< h ( x )< h (2)$
$ \Rightarrow-10< h(x)< 8 $
$ \Rightarrow|h(x)|<10 $ (option (2) is NOT true)
Now, $h^{\prime}(x)=f^{\prime}(x)-g^{\prime}(x)=3 x^2+3$
If $\left|h^{\prime}(x)\right|<6 \Rightarrow\left|3 x^2+3\right|<6$
$ \Rightarrow 3 x ^2+3<6$
$ \Rightarrow x ^2< 1$
$ \Rightarrow-1< x< 1 $ (option (3) is True)
If $x \in(-1,1)\left|f^{\prime}(x)-g^{\prime}(x)\right|<6$
option (3) is true and now to solve
$ f(x)-g(x)=0 $
$ \Rightarrow x^3+3 x-6=0 $
$ h(x)=x^3+3 x-6$
here, $h(1)=-$ ve and $h\left(\frac{3}{2}\right)=+$ ve
So there exists $x _0 \in\left(1, \frac{3}{2}\right)$ such that $f \left( x _0\right)= g \left( x _0\right)$
(option (4) is true)

A

$\left\{(2 k +1) \frac{\pi}{2}, k \in Z \right\}$

B

$\left\{ k \pi+\frac{\pi}{4}, k \in Z \right\}$

C

$\{ k \pi, k \in Z \}$

D

$R$

Solution

If its invertible, then determinant value $\neq 0$
So,
$\begin{vmatrix}e^t & e^{-t}(\sin t-2 \cos t) & e^{-t}(-2 \sin t-\cos t) \\e^t & e^{-t}(2 \sin t+\cos t) & e^{-t}(\sin t-2 \cos t) \\e^t & e^{-t} \cos t & e^{-t} \sin t\end{vmatrix} \neq 0$
$\Rightarrow e ^{ t } \cdot e ^{- t } \cdot e ^{- t }\begin{vmatrix}1 & \sin t -2 \cos t & -2 \sin t -\cos t \\ 1 & 2 \sin t +\cos t & \sin t -2 \cos t \\ 1 & \cos t & \sin t\end{vmatrix} \neq 0$
Applying, $R_1 \rightarrow R_1-R_2$ then $R_2 \rightarrow R_2-R_3$
We get
$e ^{- t }\begin{vmatrix}0 & -\sin t-\cos t & -3 \sin t+\cos t \\ 0 & 2 \sin t & -2 \cos t \\ 1 & \cos t & \sin t\end{vmatrix} \neq 0$
By expanding we have,
$ e ^{-t} \times 1\left(2 \sin t \cos t +6 \cos ^2 t +6 \sin ^2 t -2 \sin t \cos t \right) \neq 0$
$\Rightarrow e ^{-t} \times 6 \neq 0$
$ \text { for } \forall t \in R$

A

$1-\frac{3}{\sqrt{2}}+\frac{4}{\sqrt{5}}$

B

$\sqrt{5}+2 \sqrt{2}-4.5$

C

$\frac{3}{\sqrt{5}}-\frac{3}{\sqrt{2}}+1$

D

$\sqrt{5}-2 \sqrt{2}+1$

Solution

$|\cos x-\sin x| \leq y \leq \sin x$
Intersection point of $\cos x-\sin x=\sin x$
$\Rightarrow \tan x=\frac{1}{2}$
Let $\psi=\tan ^{-1} \frac{1}{2}$
So, $\tan \psi=\frac{1}{2}, \sin \psi=\frac{1}{\sqrt{5}}, \cos \psi=\frac{2}{\sqrt{5}}$

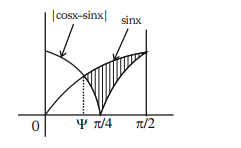
Area $ =\int\limits_\psi^{\pi / 2}(\sin x-|\cos x-\sin x|) d x$
$=\int\limits_\psi^{\pi / 4}(\sin x-(\cos x-\sin x)) d x $
$ +\int\limits_{\pi / 4}^{\pi / 2}(\sin x-(\sin x-\cos x)) d x $
$=\int\limits_\psi^{\pi / 4}(2 \sin x-\cos x) d x+\int\limits_{\pi / 4}^{\pi / 2} \cos x dx $
$=[-2 \cos x-\sin x]_\psi^{\pi / 4}+[\sin x]_{\pi / 4}^{\pi / 2} $
$ =-\sqrt{2}-\frac{1}{\sqrt{2}}+2 \cos \psi+\sin \psi+\left(1-\frac{1}{\sqrt{2}}\right) $
$ = -\sqrt{2}-\frac{1}{\sqrt{2}}+2\left(\frac{2}{\sqrt{5}}\right)+\left(\frac{1}{\sqrt{5}}\right)+1-\frac{1}{\sqrt{2}} $
$= \sqrt{5}-2 \sqrt{2}+1$

A

$[-2,-1]$

B

$\left[-2,-\frac{3}{2}\right]$

C

$\left[-1,-\frac{1}{2}\right]$

D

$\left[-\frac{3}{2},-1\right]$

Solution

$\lambda=\cos ^2 2 x-2 \sin ^4 x-2 \cos ^2 x$
convert all in to $\cos x$.
$\lambda=\left(2 \cos ^2 x-1\right)^2-2\left(1-\cos ^2 x\right)^2-2 \cos ^2 x$
$= 4 \cos ^4 x-4 \cos ^2 x+1-2\left(1-2 \cos ^2 x+\cos ^4 x\right)- 2 \cos ^2 x $
$= 2 \cos ^4 x-2 \cos ^2 x+1-2 $
$= 2 \cos ^4 x-2 \cos ^2 x-1 $
$= 2\left[\cos ^4 x-\cos ^2 x-\frac{1}{2}\right] $
$= 2\left[\left(\cos ^2 x-\frac{1}{2}\right)^2-\frac{3}{4}\right] $
$ \lambda_{\max }=\left.2\left[\frac{1}{4}-\frac{3}{4}\right]=2 \times\left(-\frac{2}{4}\right)=-1 \text { (max Value }\right) $
$ \lambda_{\min }= 2\left[0-\frac{3}{4}\right]=-\frac{3}{2}(\text { MinimumValue }) $
$ \text { So, Range }=\left[-\frac{3}{2},-1\right]$

A

89

B

84

C

86

D

79

Solution

Lets arrange the letters of OUGHT in alphabetical order.
G, H, O, T, U
Words starting with
$G ----\rightarrow 4$ !
$H ----\rightarrow 4$ !
$O ----\rightarrow 4$ !
$T G ---\rightarrow 3$ !
$T H ---\longrightarrow 3$ !
$T O G --\rightarrow 2$ !
$T O H --\rightarrow 2$ !
$T O U G H \rightarrow 1$ !
Total $=89$

A

$\frac{17}{3}$

B

$\frac{16}{3}$

C

$\frac{73}{3}$

D

$\frac{97}{3}$

Solution

$A ( a ,-2,4), B (2, b ,-3)$
$ AC : CB =2: 1$
$ \Rightarrow C \equiv\left(\frac{ a +4}{3}, \frac{2 b -2}{3}, \frac{-2}{3}\right)$
$C$ lies on $2 x - y +2=4$
$ \Rightarrow \frac{2 a+8}{3}-\frac{2 b-2}{3}-\frac{2}{3}=4 $
$ \Rightarrow a-b=2 \ldots \text { (1) }$
Also $OC =\sqrt{5}$
$\Rightarrow\left(\frac{ a +4}{3}\right)^2+\left(\frac{2 b-2}{3}\right)^2+\frac{4}{9}=5$....(2)
Solving, (1) and (2)
$ (b+6)^2+(2 b-2)^2=41 $
$\Rightarrow 5 b^2+4 b-1=0 $
$\Rightarrow b=-1 \text { or } \frac{1}{5}$
$\Rightarrow a=1 \text { or } \frac{11}{5}$
But $ab < 0 \Rightarrow( a , b )=(1,-1)$
$ C \equiv\left(\frac{5}{3}, \frac{-4}{3}, \frac{-2}{3}\right), P \equiv(2,-1,-3)$
$CP ^2=\frac{1}{9}+\frac{1}{9}+\frac{49}{9}=\frac{51}{9}=\frac{17}{3}$

A

$\frac{5}{\sqrt{2}}$

B

$\frac{1}{5}$

C

$\frac{1}{\sqrt{2}}$

D

$\frac{3}{\sqrt{2}}$

Solution

$\vec{ a } \times \vec{ b }=15 \hat{ i }-20 \hat{ j }-25 \hat{ k }$
Let $ \vec{c}=x \hat{i}+y \hat{j}+z \hat{k}$
$\Rightarrow 15 x-20 y-25 z+25=0$
$\Rightarrow 3 x-4 y-5 z=-5$
Also $x+y+z=4$
and $\frac{\vec{ c } \cdot \vec{ a }}{|\vec{ a }|}=1 \Rightarrow 4 x+3 y=5$
$\Rightarrow \vec{c}=2 \hat{i}-\hat{j}+3 \hat{k}$
Projection of $\vec{ c }$
or $\vec{ b }=\frac{25}{5 \sqrt{2}}=\frac{5}{\sqrt{2}}$

A

16

B

28

C

10

D

22

Solution

Point on $L _1 \equiv(\lambda+1,2 \lambda+2, \lambda-3)$
Point on $L _2 \equiv(2 \mu+ a , 3 \mu-2, \mu+3)$
$\lambda-3=\mu+3 \Rightarrow \lambda=\mu+6$...(1)
$2 \lambda+2=3 \mu-2 \Rightarrow 2 \lambda=3 \mu-4$...(2)
Solving, (1) and (2)
$\Rightarrow \lambda=22 \& \mu=16 $
$\Rightarrow P \equiv(23,46,19)$
$\Rightarrow a =-9$
Distance of $P$ from $z =-9$ is $28$

A

$\pi \log _e 2$

B

$\frac{1}{2} \log _{ e } 2$

C

$\frac{\pi}{4} \log _{ e } 2$

D

$\frac{\pi}{2} \log _{ e } 2$

Solution

$I =\int\limits_{1 / 2}^2 \frac{\tan ^{-1} x }{ x } dx$...(i)
Put $ x =\frac{1}{ t } dx =-\frac{1}{ t ^2} dt$
$ I =-\int\limits_2^{1 / 2} \frac{\tan ^{-1} \frac{1}{ t }}{\frac{1}{ t }} \cdot \frac{1}{ t ^2} dt =-\int\limits_2^{1 / 2} \frac{\tan ^{-1} \frac{1}{ t }}{ t } dt $
$ I =\int\limits_{1 / 2}^2 \frac{\cot ^{-1} t }{ t } dt =\int\limits_{1 / 2}^2 \frac{\cot ^{-1} x }{ x } dx \ldots . .(ii)$
Add both equation
$2 I= \int\limits_{1 / 2}^2 \frac{\tan ^{-1} x+\cot ^{-1} x}{x} d x=\frac{\pi}{2} \int\limits_{1 / 2}^2 \frac{d x}{x}=\frac{\pi}{2}(\ell \operatorname{nn} 2)_{1 / 2}^2$
$ =\frac{\pi}{2}\left(\ell \ln 2-\ell \ln \frac{1}{2}\right)=\pi \ell \operatorname{n} 2$
$I =\frac{\pi}{2} \ell \ln 2$

A

$\frac{9}{\sqrt{5}}$

B

$5 \sqrt{3}$

C

$\frac{3}{2} \sqrt{5}$

D

$3 \sqrt{5}$

Solution

$y^2=3 x$
Tangent $P \left( x _1, y _1\right)$ is parallel to $x +2 y =1$
Then slope at $P =-\frac{1}{2}$
$2 y \frac{ dy }{ dx }=3$
$ \Rightarrow \frac{ dy }{ dx }=\frac{3}{2 y }=-\frac{1}{2} $
$ \Rightarrow y_1=-3$
Coordinates of $P (3,-3)$
Similarly $Q \left(\frac{4}{\sqrt{3}}, \frac{1}{\sqrt{5}}\right), R \left(-\frac{4}{\sqrt{5}}, \frac{-1}{\sqrt{5}}\right)$
Area of $\triangle PQR$
$=\frac{1}{2}\begin{vmatrix}3 & -3 & 1 \\ \frac{4}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 1 \\ -\frac{4}{\sqrt{5}} & -\frac{1}{\sqrt{5}} & 1\end{vmatrix}$
$=\frac{1}{2}\left[3\left(\frac{2}{\sqrt{5}}\right)+3\left(\frac{8}{\sqrt{5}}\right)+0\right]=\frac{30}{2 \sqrt{5}}=3 \sqrt{5}$

A

$\frac{4+ e ^2}{4}$

B

$\frac{1+ e ^2}{4}$

C

$\frac{2+ e ^2}{2}$

D

$\frac{1+ e ^2}{2}$

Solution

$ x \log _e x \frac{d y}{d x}+y=x^2 \log _e x,(x>1)$
$ \Rightarrow \frac{d y}{d x}+\frac{y}{x \ln x}=x$
Linear differential equation
$\text { I.F. }=e^{\int \frac{1}{x \ln x} d x}=|\ln x|$
$\therefore$ Solution of differential equation
$y|\ln x| =\int x|\ln x| d x$
$ =|\ln x| \frac{x^2}{2}-\int \frac{1}{x} \cdot \frac{x^2}{2} d x$
$\Rightarrow y|\ln x| =|\ln x|\left(\frac{x^2}{2}\right)-\frac{x^2}{4}+c$
For constant
$y(2)=2 \Rightarrow c=1$
So, $y(x)=\frac{x^2}{2}-\frac{x^2}{4|\ln x|}+\frac{1}{|\ln x|}$
Hence, $y(e)=\frac{ e ^2}{2}-\frac{ e ^2}{4}+1=1+\frac{ e ^2}{4}$

A

472

B

432

C

507

D

400

Solution

Total 3 digit number $=900$
Divisible by $3=300$
(Using $\frac{900}{3}=300$ )
Divisible by $4=225$
(Using $\frac{900}{4}=225$ )
Divisible by $3$ & $4=108, \ldots$.
(Using $\frac{900}{12}=75$ )
Number divisible by either 3 or 4
$=300+2250-75=450$
We have to remove divisible by $48$ ,
$144,192, \ldots ., 18$ terms
Required number of numbers $=450-18=432$

A

not reflexive

B

transitive but not symmetric

C

symmetric but not transitive

D

an equivalence relation

Solution

$a R a \Rightarrow 5 a$ is multiple it 5
So reflexive
$a R b \Rightarrow 2 a +3 b =5 \alpha \text {, }$
Now $b \,R \,a$
$2 b+3 a =2 b+\left(\frac{5 \alpha-3 b}{2}\right) \cdot 3 $
$=\frac{15}{2} \alpha-\frac{5}{2} b=\frac{5}{2}(3 \alpha-b)$
$ =\frac{5}{2}(2 a+2 b-2 \alpha)$
$=5(a+b-\alpha)$
Hence symmetric
$ \text { a R b } \Rightarrow 2 a+3 b=5 \alpha$
$ \text { b R c } \Rightarrow 2 b+3 c=5 \beta $
$ \text { Now } 2 a+5 b+3 c=5(\alpha+\beta)$
$ \Rightarrow 2 a +5 b +3 c =5(\alpha+\beta) $
$ \Rightarrow 2 a+3 c=5(\alpha+\beta-b) $
$ \Rightarrow a R c $
Hence relation is equivalence relation.

A

8200

B

8000

C

8400

D

8100

Solution

Given for $x \geq 2$
$ f(1)+2 f(2)+\ldots \ldots+x f(x)=x(x+1) f(x)$
$\text { replace } x \text { by } x+1 $
$\Rightarrow x(x+1) f(x)+(x+1) f(x+1)$
$ =( x +1)( x +2) f ( x +1)$
$ \Rightarrow \frac{x}{f(x+1)}+\frac{1}{f(x)}=\frac{(x+2)}{f(x)}$
$ \Rightarrow x f(x)=(x+1) f(x+1)=\frac{1}{2}, x \geq 2$
$ f (2)=\frac{1}{4}, f (3)=\frac{1}{6}$
$ \text { Now } f(2022)=\frac{1}{4044}$
$f(2028)=\frac{1}{4056} $
$ \text { So, } \frac{1}{f(2022)}+\frac{1}{f(2028)}=4044+4056=8100 $

Solution

$N$ should be divisible by 2 but not by 3
$N =$ (Numbers divisible by 2 ) $-$ (Numbers divisible by 6$)$
$N =\frac{9000}{2}-\frac{9000}{6}=4500-1500=3000$

Solution

$S_1: y^2=2 x $
$S_2: x^2+y^2=4 x$
$P (2,2)$ is common point on $S _1 \& S _2$
$T_1$ is tangent to $S_1$ at $P $
$\Rightarrow T_1: y \cdot 2=x+2$
$\Rightarrow T_1: x-2 y+2=0$
$T_2$ is tangent to $S_2$ at $P $
$ \Rightarrow T_2: x \cdot 2+y \cdot 2=2(x+2)$
$\Rightarrow T_2: y=2$
$\& L _3: x + y +2=0$ is third line

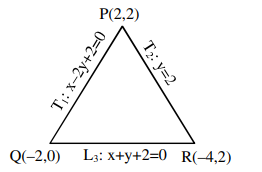
$ PQ = a =\sqrt{20} $
$ QR = b =\sqrt{8} $
$ RP = c =6$
Area $(\triangle PQR )=\Delta=\frac{1}{2} \times 6 \times 2=6$
$\therefore r =\frac{ abc }{4 \Delta}=\frac{\sqrt{160}}{4}=\sqrt{10} $
$\Rightarrow r ^2=10$

Solution

The given line is polar or $P(2, \beta)$ w.r.t. given circle
$x^2+y^2-4 x-6 y-3=0$
Chord or contact
$ \alpha x +\beta y -2( x +\alpha)-3( y +\beta)-3=0$
$ \Rightarrow(\alpha-2) x +(\beta-3) y -(2 \alpha+3 \beta+3)=0$....(i)
$\because$ But the equation of chord of contact is given
as : $x+y-3=0$...(ii)
comparing the coefficients
$\frac{\alpha-2}{1}=\frac{\beta-3}{1}=-\left(\frac{2 \alpha+3 \beta+3}{-3}\right)$
On solving $\alpha=-6$
$\beta=-5$
Now $ 4 \alpha-7 \beta=11$

Solution

As, $ S =\frac{ b _1}{2}+\frac{ b _2}{2^2}+\ldots \ldots .+\frac{ b _9}{2^9}+\frac{b_{10}}{2^{10}} $
$\Rightarrow \frac{ S }{2}= \frac{ b _1}{2^2}+\frac{ b _2}{2^3}+\ldots \ldots .+\frac{b_9}{2^{10}}+\frac{b_{10}}{2^{11}}$
subtracting
$\Rightarrow \frac{ S }{2}=\frac{ b _1}{2}+\left(\frac{ a _1}{2^2}+\frac{ a _2}{2^3} \ldots \ldots .+\frac{ a _9}{2^{10}}\right)-\frac{ b _{10}}{2^{11}}$
$ \Rightarrow S = b _1-\frac{ b _{10}}{2^{10}}+\left(\frac{ a _1}{2}+\frac{ a _2}{2^2} \ldots \ldots .+\frac{ a _9}{2^9}\right) $
$ \Rightarrow \frac{ S }{2}=\frac{ b _1}{2}-\frac{ b _{10}}{2^{11}}+\left(\frac{ a _1}{2^2}+\frac{ a _2}{2^3} \ldots \ldots .+\frac{ a _9}{2^{10}}\right)$
subtracting
$ \Rightarrow \frac{S}{2}=\frac{b_1}{2}-\frac{b_{10}}{2^{11}}+\left(\frac{a_1}{2}-\frac{a_9}{2^{10}}\right)+\left(\frac{1}{2^2}+\frac{2}{2^3}+\ldots+\frac{8}{2^9}\right) $
$ \Rightarrow \frac{S}{2}=\frac{a_1+b_1}{2}-\frac{\left(b_{10}+2 a_9\right)}{2^{11}}+\frac{T}{4}$
$ \Rightarrow 2 S=2\left(a_1+b_1\right)-\frac{\left(b_{10}+2 a_9\right)}{2^9}+T $
$\Rightarrow 2^7(2 S-T)=2^8\left(a_1+b_1\right)-\frac{\left(b_{10}+2 a_9\right)}{4}$

Solution

$y=\frac{x-a}{(x+b)(x-2)}$
At point $(1,-3)$,
$-3 =\frac{1-9}{(1+b)(1-2)} $
$\Rightarrow 1-a =3(1+b)$....(1)
Now, $y=\frac{x-a}{(x+b)(x-2)}$
$\Rightarrow \frac{d y}{d x}=\frac{(x+b)(x-2) \times(1)-(x-a)(2 x+b-2)}{(x+b)^2(x-2)^2}$
At $(1,-3)$ slope of normal is $\frac{1}{4}$ hence $\frac{d y}{d x}=-4$,
So, $-4=\frac{(1+b)(-1)-(1-a) b}{(1+b)^2(-1)^2}$
Using equation (1)
$ \Rightarrow-4=\frac{(1+b)(-1)-3(b+1) b}{(1+b)^2}$
$ \Rightarrow-4=\frac{(-1)-3 b}{(1+b)}(b \neq-1) $
$ \Rightarrow b=-3$
So, $a =7$
Hence, $a+b=7-3=4$

Solution

$\begin{bmatrix}2 & 1 \\ 3 & \frac{3}{2}\end{bmatrix}\begin{bmatrix}a & b \\ b & c\end{bmatrix}=\begin{bmatrix}1 & 2 \\ \alpha & \beta\end{bmatrix}$
Now $a c-b^2=2$ and $2 a+b=1$
and $2 b+c=2$
solving all these above equations we get
$\frac{1-b}{2} \times\left(\frac{2-2 b}{1}\right)-b^2=2 $
$ \Rightarrow(1-b)^2-b^2=2 $
$ \Rightarrow 1-2 b=2$
$ \Rightarrow b=-\frac{1}{2} \text { and } a=\frac{3}{4} \text { and } c=3$
Hence $\alpha=3 a +\frac{3 b }{2}=\frac{9}{4}-\frac{3}{4}=\frac{3}{2}$
and $\beta=3 b+\frac{3 c}{2}=-\frac{3}{2}+\frac{9}{2}=3$
also $s = a + c =\frac{15}{4}$
$\therefore \frac{\beta s}{\alpha^2}=\frac{3 \times 15}{4 \times \frac{9}{4}}=5$

Solution

Given that
$c_k=a_k+b_k$ and $a_1=b_1=4$
also $a_2=4 r_1 \,\,\, a_3=4 r_1^2 $
$b_2=4 r_2 \,\,\, b_3=4 r_2^2$
Now $c_2=a_2+b_2=5$ and $c_3=a_3+b_3=\frac{13}{4}$
$\Rightarrow r _1+ r _2=\frac{5}{4}$ and $r _1^2+ r _2^2=\frac{13}{16}$
Hence $r_1 r_2=\frac{3}{8} \,\,\,\, $ which gives $r_1=\frac{1}{2} \,\,\,\, \& \,\,\,\,r_2=\frac{3}{4}$
$\displaystyle\sum_{ k =1}^{\infty} c _{ k }-\left(12 a _6+8 b _4\right)$
$ =\frac{4}{1-r_1}+\frac{4}{1-r_2}-\left(\frac{48}{32}+\frac{27}{2}\right) $
$=24-15=9$

Solution

$ \overline{ x }=\frac{\displaystyle\sum_{ i =11}^{41} i }{31}=\frac{11+41}{2}=26 \quad(31 \text { elements }) $
$ \overline{ y }=\frac{\displaystyle\sum_{ j =61}^{91} j }{31}=\frac{61+91}{2}=76 \quad(31 \text { elements) }$
Combined mean, $ \mu=\frac{31 \times 26+31 \times 76}{31+31} $
$=\frac{26+76}{2}=51 $
$ \sigma^2=\frac{1}{62} \times\left(\displaystyle\sum_{i=1}^{31}\left(x_i-\mu\right)^2+\displaystyle\sum_{i=1}^{31}\left(y_i-\mu\right)^2\right)=705 $
Since, $x_i \in X$ are in A.P. with 31 elements & common difference 1 , same is $y _{ i } \in y$, when written in increasing order.
$ \therefore \displaystyle\sum_{ i =1}^{31}\left( x _{ i }-\mu\right)^2=\displaystyle \sum_{ i =1}^{31}\left( y _{ i }-\mu\right)^2 $
$=10^2+11^2+\ldots . .+40^2 $
$ =\frac{40 \times 41 \times 81}{6}-\frac{9 \times 10 \times 19}{6}=21855$
$ \therefore\left|\overline{ x }+\overline{ y }-\sigma^2\right|=|26+76-705|=603$

Solution

$ \alpha=8-14 i$
$ z=x+i y $
$ a z=(8 x+14 y)+i(-14 x+8 y)$
$z +\overline{ z }=2 x\,\,\, z -\overline{ z }=2 iy$
Set A: $\frac{2 i(-14 x+8 y)}{i(4 x y-112)}=1$
$ (x-4)(y+7)=0 $
$ x=4 \text { or } y=-7$
Set B: $x^2+(y+3)^2=16$
when $x=4 \,\,\, y=-3$
when $y=-7 \,\,\, x=0$
$\therefore A \cap B =\{4-3 i , 0-7 i \}$
So, $\displaystyle\sum_{z \in A \cap B}(\text{Rez}-\text{Im} z )=4-(-3)+(0-(-7))=14$

Solution

Given equation can be rearranged as
$x\left(x^6+3 x^4-13 x^2-15\right)=0$
clearly $x=0$ is one of the root and other part can be observed by replacing $x^2= t$ from which we have $t^3+3 t^2-13 t-15=0$
$\Rightarrow (t-3)\left(t^2+6 t+5\right)=0$
So, $ t=3, t=-1, t=-5$
Now we are getting $x^2=3, x^2=-1, x^2=-5$
$\Rightarrow x=\pm \sqrt{3}, x=\pm i , x=\pm \sqrt{5} i$
From the given condition $\left|\alpha_1\right| \geq\left|\alpha_2\right| \geq \ldots \geq\left|\alpha_7\right|$
We can clearly say that $\left|\alpha_\tau\right|=0$ and
and $\left|\alpha_6\right|=\sqrt{5}=\left|\alpha_5\right|$
and
$\left|\alpha_4\right|=\sqrt{3}=\left|\alpha_3\right|$ and $\left|\alpha_2\right|=1=\left|\alpha_1\right|$
So we can have, $\alpha_1=\sqrt{5} i , \alpha_2=-\sqrt{5} i , \alpha_3=\sqrt{3} i$,
$\alpha_4=-\sqrt{3}, \alpha_5= i , \alpha_6=- i$
Hence
$\alpha_1 \alpha_2-\alpha_3 \alpha_4 +\alpha_5 \alpha_6$
$ =1-(-3)+5=9$