JEE Main Physics Question Paper with Solution 2023 June 29th Shift 2 - Evening
A
10 m
B
20 m
C
30 m
D
40 m
Solution
$u =0,$ Say acceleration is a
For t s $10=\frac{1}{2}$ at $^{2}$
For $2 t s \,10+ x =\frac{1}{2} a (2 t )^{2}$
$\frac{10+x}{10}=\frac{4}{1}$
$x=30\, m$
A
$125.7^{\circ} C$
B
$91.7^{\circ} C$
C
$425.7^{\circ}$
D
$152.7^{\circ} C$
Solution
$\Delta \ell=6.241-6.230=0.011\, cm$
$\Delta \ell=\ell \alpha \Delta \theta$
$0.011=6.230 \times 1.4 \times 10^{-5}(\theta-27)$
$\theta-27=\frac{0.011 \times 10^{5}}{6.230 \times 1.4}$
$\theta \approx 153.11$ nearest is $152.7^{\circ} C$.
A
$x=d$
B
$x=\frac{d}{2}$
C
$x=\frac{d}{\sqrt{2}}$
D
$x=\frac{d}{2 \sqrt{2}}$
Solution

$F =\frac{ KQq }{\left( x ^{2}+\frac{ d ^{2}}{4}\right)}$
Net force on $g =2 F \cos \theta$
$F _{\text {net }}=\frac{2 KQqx }{\left( x ^{2}+\frac{ d ^{2}}{4}\right)^{3 / 2}}$
For maximum $F _{ net }$
$\frac{ d F _{\text {net }}}{ dx }=0$
we get $x=\frac{d}{2 \sqrt{2}}$
A
$\theta=\sin ^{-1}\left(\frac{3}{4}\right)$
B
$\theta >\sin ^{-1}\left(\frac{2}{3}\right)$
C
$\theta< \sin ^{-1}\left(\frac{3}{4}\right)$
D
$\theta >\sin ^{-1}\left(\frac{3}{4}\right)$
Solution
$\sin i _{ c }=\frac{ n _{ r }}{ n _{ d }}=\frac{ C _{ d }}{ C _{ r }}=\frac{1.5 \times 10^{10}}{2 \times 10^{10}}$

$\sin i_{c}=\frac{3}{4}$
$i_{c}=\sin ^{-1}\left(\frac{3}{4}\right)$
for T I R $ \theta>i_{c}$
$\theta>\sin ^{-1}\left(\frac{3}{4}\right)$
A
174 and 71
B
174 and 69
C
172 and 69
D
172 and 71
Solution
Say for $D _{4}$ Atomic $No = Z$
Mass Number $=$ A
$A =182-4-4=174$
$Z =74-2+1-2=71$
A
1.90 eV
B
3.27 eV
C
3.60 eV
D
3.42 eV
Solution
For maximum KE we will take higher frequency
$\left( f =\frac{9 \times 10^{15}}{2 \pi} Hz \right)$
$K _{\max }= hf -\phi$
$=\frac{9 \times 10^{15} \times 4.14 \times 10^{-15}}{2 \pi}-2.50$
$3.43\, eV \text { nearest is } 3.42\, eV$
A
$1 / 2$
B
$1 / 3$
C
$1 / 4$
D
$1 / 6$
Solution
In $t _{1}$ time energy becomes half so charge will become $\frac{1}{\sqrt{2}}$ time
$q = Q _{0} e ^{-\frac{ t _{1}}{ RC }}=\frac{ Q _{0}}{\sqrt{2}}$
and $q = Q _{0} e ^{-\frac{ t _{1}}{ RC }}=\frac{ Q _{0}}{8}=\left(\frac{ Q _{0}}{\sqrt{2}}\right)^{6}$
$t _{2}=6 t _{1}$
$\frac{ t _{1}}{ t _{2}}=\frac{1}{6}$
A
$W _{1}< W _{2}< W _{3}$
B
$W _{2}< W _{3}< W _{1}$
C
$W _{3}< W _{1}< W _{2}$
D
$W _{2}< W _{1}< W _{3}$
Solution

Area under curve is work
$W _{2}< W _{1}< W _{3}$
A
30 A in the same direction.
B
30 A in the opposite direction.
C
60 A in the opposite direction.
D
300 A in the opposite direction.
Solution

$B$ at $O =2 \frac{\mu_{0} I }{2 \pi r }$
$\frac{2 \times 4 \pi \times 10^{-7} I }{2 \pi 4 \times 10^{-2}}=3 \times 10^{-4} T$
$I =30\, A$ in opp. direction
A
40 hours
B
36 hours
C
30 hours
D
25 hours
Solution
$T =\frac{2 \pi}{\sqrt{ GM }} r ^{3 / 2}$
$\frac{ T _{1}}{ T _{2}}=\left(\frac{ r _{1}}{ r _{2}}\right)^{3 / 2}=\left(\frac{1}{3}\right)^{3 / 2}$
$T _{2}= T _{1} 3 \sqrt{3}=21 \sqrt{3}$ hours
$\approx 36$ hours
A
125 m
B
250 m
C
375
D
500 m
Solution
Range $d =\sqrt{2 Rh }$
$d _{2}=2 d _{1}$
$\sqrt{2 Rh _{2}}=2 \sqrt{2 Rh _{1}}$
$h _{2}=4 h _{1}=500\, m$
$\Delta h =500\, m -125\, m =375\, m$
A
97.23 cm
B
25.3 cm
C
99.4 cm
D
406.1 cm
Solution
$\omega=\sqrt{\frac{ g }{\ell}}=\pi$
$\frac{ g }{\ell}=\pi^{2} \Rightarrow \ell=\frac{ g }{\pi^{2}}$
$\ell=\frac{980}{\pi^{2}} \approx 99.4\, cm$
A
$72 \times 10^{5}$
B
$32 \times 10^{5}$
C
$27 \times 10^{4}$
D
$54 \times 10^{4}$
Solution
No of moles of $H _{2}=8$ moles
No of moles of $O _{2}=4$ moles
Total moles $=12$ moles
At STP 1 mole occupy $=22.4 \ell=22.4 \times 10^{3} cm ^{3}$
12 moles will occupy $=12 \times 22.4 \times 10^{3} cm ^{3}$ $\approx 26.8 \times 10^{4} cm ^{3}$
A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are incorrect.
C
Statement I is correct but Statement II is incorrect
D
Statement I is incorrect but Statement II is correct
Solution
Electric field can change speed and kinetic energy but magnetic field can not change speed $\triangle KE$. Because magnetic force is always $\perp$ to velocity.
A
$1\, ms ^{-2}$
B
$1 / 5\, ms ^{-2}$
C
$4 / 5\, ms ^{-2}$
D
$8 / 11\, ms ^{-2}$
Solution
For $4 kg$ block
$4 g - T =4 a$
For $40 kg$ block
$T -40 g \times 0.02=40 a$
Adding both eq.
$40-8=44 a$
$a=\frac{32}{44}=\frac{8}{11} m / s ^{2}$
A
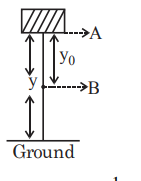
$\frac{1}{2} mg y _{0}^{2}$
B
$\frac{1}{2} mgy ^{2}$
C
$m g\left( y - y _{0}\right)$
D
$m g y_{0}$
Solution
Work done by gravity $= K _{ B }- K _{ A }$
$mgy _{0}= K _{ B }-0$
$K _{ B }= mgy _{0}$
A
$\frac{g}{4}$
B
$\frac{ g }{2}$
C
$\frac{3 g }{4}$
D
$g$
Solution

$m g-N=m a$
$a=g-\frac{g}{4}$
$a=\frac{3 g}{4}$
A
$3\, Vm ^{-1}$, directed along positive $x$-axis.
B
$3\,Vm ^{-1}$, directed along negative $x$-axis.
C
$6\, Vm ^{-1}$, directed along positive $x$-axis.
D
$6\, Vm ^{-1}$, directed along negative $x$-axis.
Solution
$E _{ x }=-\frac{\partial V }{\partial x }=-6 x$
At $(1,0,3)$
$\vec{ E }=-6 V / m \hat{ i }$
A
$2\, \Omega$
B
$4\, \Omega$
C
$6\, \Omega$
D
$8\, \Omega$
Solution

$I _{2}=\frac{ E }{\frac{ r }{2}+2}=\frac{2 E }{ r +4}$
$I _{1}= I _{2}$
$2 r +2= r +4$
$2 r - r =2\, \Omega$
$\Rightarrow r =2\, \Omega$
A
25 m
B
50 m
C
100 m
D
200 m
Solution
$R =\frac{ u ^{2} \sin 2 \theta}{ g } R _{\max }=\frac{ u ^{2}}{ g }=100$
$H _{\max }=\frac{ u ^{2}}{2 g }=\frac{100}{2}=50\, m$
Answer: 180
Solution
Measured diameter $= MSR + VSR \times VC$
$=1.7+0.01 \times 5$
$=1.75$
Corrected $=$ Measured $-$ Error
$=1.75-(-0.05)$
$=1.80\, cm$
$=180 \times 10^{-2} cm$
$180$
Answer: 20
Solution
Speed after falling through height $h$
Should be equal to terminal velocity
$\sqrt{2 g h}=\frac{2}{9} \frac{ r ^{2}( d -\rho) g }{\eta}$
$\sqrt{2 gh }=\frac{2}{9} \frac{10^{-8}(10000-1000) \times 10}{10^{-5}}$
$=\frac{2}{9} \times 10^{-8} \frac{9 \times 10^{4}}{10^{-5}}=20$
$2 \times 10 \times h =400$
$h =20\, m$
Answer: 104
Solution
For first resonance
$\ell_{1}+ e =\frac{\lambda}{4}$
$\lambda=\frac{336}{400} \times 100\, cm =84\, cm$
$\Rightarrow \frac{\lambda}{4}=21\, cm$
$e =21-20=1\, cm$
For third resonance
$\ell_{3}+ e =\frac{5 \lambda}{4}=105\, cm$
$\Rightarrow \ell_{3}=104\, cm$
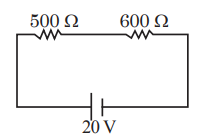
Answer: 8
Solution
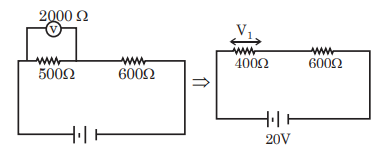
$I =\frac{20}{1000} A$
$V _{1}= I \times 400=\frac{20}{1000} \times 400$
$=8\, V$
Answer: 14
Solution

Work done by Electric field $= K _{ f }- K _{ i }$
$\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}=-1.6-10^{-19} \times 0.4$
$\frac{1}{2} 9 \times 10^{-31}\left( v ^{2}- u ^{2}\right)=-0.64 \times 10^{-19}$
$u^{2}-v^{2}=\frac{2 \times 0.64 \times 10^{12}}{9}$
$v^{2}=\left(36-\frac{128}{9}\right) \times 10^{10}$
$v =\frac{14}{3} \times 10^{5} m / s$
$x=14$
Answer: 8
Solution
Displacement Current $=$ Conduction Current
$=\frac{ dq }{ dt }$
$I_{d}=\frac{\epsilon_{0} A }{ d } \frac{ dV }{ dt }$
$d=\frac{8.85 \times 10^{-12} \times 4 \times 10^{-3} \times 10^{6}}{4.425 \times 10^{-6}}$
$=8\, mm$
$X =8$
Answer: 8
Solution

$\ell=2 \pi r \Rightarrow \frac{\ell}{ r }=2 \pi$

$\frac{ I _{1}}{ I _{2}}=\frac{2}{3}\left(\frac{\ell}{ r }\right)^{2}$
$=\frac{2}{3} \times 4 \pi^{2}=\frac{8 \pi^{2}}{3}$
$x =8$
Answer: 20
Solution
$T 1 / 2=5$ year
$N = N _{0}\left(\frac{1}{2}\right)^{\text {No of half lives }}$
$\frac{ N }{ N _{0}}=\frac{1}{16}=\left(\frac{1}{2}\right)^{4}$
Time $=4$ half lives $=20$ years
Answer: 600
Solution
$\beta=\frac{\lambda D }{ d }$
$\Delta \beta=\frac{\lambda}{ d } \Delta D$
$\lambda=\frac{\Delta \beta . d }{\Delta D }$
$=\frac{3 \times 10^{-5} \times 1 \times 10^{-3}}{5 \times 10^{-2}}$
$=60 \times 10^{-8}=600 \times 10^{-9} m$
$=600\, nm$
Answer: 500
Solution
If Current is in phase with emf then the frequency of source
$=\frac{1}{2 \pi \sqrt{ LC }}$ (Resonant frequency)
$\frac{1}{2 \pi \sqrt{\frac{1}{2} \times 10^{-3} \times 2 \times 10^{-4}}}$
$=\frac{1}{2 \pi} \times \sqrt{10} \times 1000=500\, Hz$
JEE Main Chemistry Question Paper with Solution 2023 June 29th Shift 2 - Evening
A
$0.005613$
B
$0.00561$
C
$0.0056$
D
$0.006$
Solution
Reported answer should not be more precise than least precise term in calculations, so there should be three significant figures in reported answer.
A
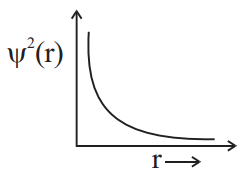
B
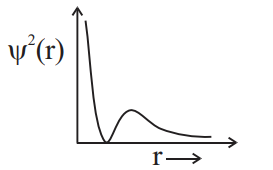
C
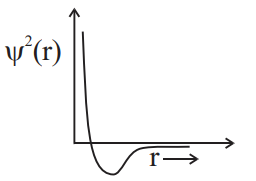
D
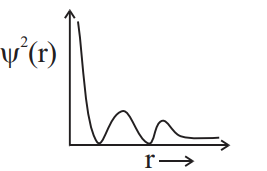
Solution
For $2 s$, number of radial nodes $=2-0-1=1$ and value of $\psi^{2}$ is always positive.
A
They are isoelectronic and only two have tetrahedral structures
B
They are isoelectronic and all have tetrahedral structures
C
Only two are isoelectronic and all have tetrahedral structures
D
Only two are isoelectronic and only two have tetrahedral structures
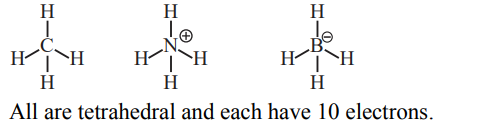
A
$2.25$
B
$6.24$
C
$12.13$
D
$15.24$
Solution
$PCl _{5}=5$ mole
$Ar =4$ mole
$P _{\text {Total }}=\frac{9 \times 0.82 \times 610}{100}=4.5\, atm$
$P _{ PCl _{5}}=\frac{5 \times 4.5}{9}=2.5 ; P _{ Ar }=\frac{4 \times 4.5}{9}=2$

$P _{\text {total }}=2.5- P + P + P + P _{ Ar }=6$
$P =1.5$
$K _{ p }=\frac{1.5 \times 1.5}{1}=2.25$
A
$36\, mmol\, L ^{-1}$
B
$36 \,mol\, L ^{-1}$
C
$1440 \,mol \,L ^{-1}$
D
$1440 \,mmol\, L ^{-1}$
Solution
Here $42.12 \%(w / v)$
$\Rightarrow 42.12$ gram salt in $100 ml$ water
$\Rightarrow 421.2$ gram salt $( NaCl )$ in $1000 ml$ or 1 lit water
$\Rightarrow \frac{421.2}{58.5}=7.2$ moles of salt
$7.2$ moles $\rightarrow 10$ hours
$x$ moles $\rightarrow 2$ hours
$
\begin{array}{l}
\Rightarrow x=\frac{7.2 \times 2}{10}=1.44 mol / L \\
\Rightarrow x=1440 mmol / L
\end{array}
$
A
Both A and R are correct and R is the correct explanation of A.
B
Both A and R are correct but R is NOT the correct explanation of A.
C
A is correct but R is not correct.
D
A is not correct but R is correct
Solution
Ionisation energy $= N > O$.
In oxygen atom, 2 of the $42 p$ electrons must occupy the same $2 p$ orbital resulting in an increased electron electron-repulsion.
A
A-I, B-II, C-III, D-IV
B
A-III, B-IV, C-II, D-I
C
A-IV, B-III, C-I, D-II
D
A-I, B-II, C-IV, D-III
Solution
Siderite $- FeCO _{3}$
Malachite $- CuCO _{3} \cdot Cu ( OH )_{2}$
Calamine $- ZnCO _{3}$
Sphalerite - ZnS
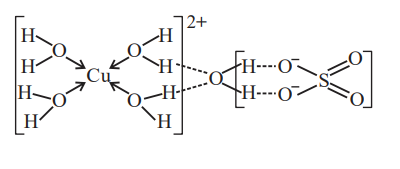
A
Both Statement I and Statement II are correct
B
Both Statement I and Statement II are incorrect
C
Statement I is correct but Statement II is incorrect
D
Statement I is incorrect but Statement II is correct
A
washing soda only.
B
washing soda and caustic soda only.
C
washing soda and baking soda only.
D
baking soda, caustic soda and washing soda
Solution
Baking soda $\rightarrow NaHCO _{3}$
Washing soda $\rightarrow Na _{2} CO _{3} \cdot 10 H _{2} O$
Caustic soda $\rightarrow NaOH$
A
0 , triangular planar.
B
1, pyramidal.
C
2, bent T-shape.
D
1, bent T-shape
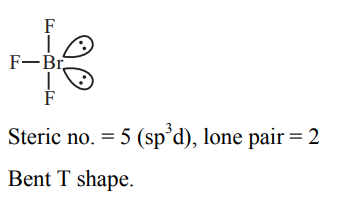
A
$NaBH _{4}$
B
$LiBH _{4}$
C
$B _{2} H _{6}$
D
$Na _{2} B _{4} O _{7}$
Solution
$Na _{2} B _{4} O _{7}$ gives $H _{3} BO _{3}$ and $NaOH$ (strong base) in water.
A
$2 SO _{2}+ O _{2} \rightarrow 2 SO _{3}$
B
$SO _{2}+ O _{3} \rightarrow SO _{3}+ O _{2}$
C
$SO _{2}+ H _{2} O _{2} \rightarrow H _{2} SO _{4}$
D
$2 SO _{2}+ O _{2}+2 H _{2} O \rightarrow 2 H _{2} SO _{4}$
Solution
$2 SO _{2}+ O _{2}+2 H _{2} O \rightarrow 2 H _{2} SO _{4}$ (Acid rain)
A
alkylated product with ortho and para substitution.
B
secondary amine after acidic treatment.
C
an amide product.
D
positively charged nitrogen at benzene ring.

A
Both A and B are correct and R is the correct explanation of A.
B
Both A and B are correct but R is NOT the correct explanation of A.
C
A is correct but R is not correct.
D
A is not correct but R is correct.

A
secondary structure
B
tertiary structure
C
primary structure
D
quaternary structure
Solution
Primary structure of protein is unaffected by physical 'or' chemical changes.
A
antiseptic
B
pesticide
C
disinfectant
D
narcotic analgesic
Solution
Antiseptic Dettol is mixture of chloroxylenol and terpineol.
A
$I ^{-}$
B
$SO _{3}^{2-}$
C
$S ^{2-}$
D
$NO _{2}^{-}$

Answer: 29
Solution
$V =\frac{ nRT }{ P }=\frac{0.90 \times 0.82 \times 300 \times 760}{18 \times 32}=29.21$
Answer: 195
Solution
$N _{2} O$ moles $=\frac{2.2}{44}=\frac{1}{20}$
$\Delta H = nC _{ p } \Delta T =\frac{1}{20} \times 100(-40)=-200 \,J$
$\Delta U = q _{ p }+ w$
$W =- P _{ ext } \Delta V$
$W =-1 \frac{(167.75-217.1)}{1000} \times 101.3\, J$
$W =+5 J$
$\Delta U =-200+5=-195 \,J$
Answer: 3
Solution
$\Delta T _{ b }= iK _{ b } m$
$\Delta T _{ f }= iK _{ f } m$
$\frac{4}{4}=\frac{ K _{ b } 1.5}{ K _{ f } 4.5}$
$\frac{ K _{ b }}{ K _{ f }}=3$
Answer: 7
Solution
$H _{2}( g )+ Cu ^{2+}($ aq. $) \rightarrow 2 H ^{+}($aq. $)+ Cu ( s )$
$0.31=0.34-\frac{0.06}{2} \log \frac{\left[ H ^{+}\right]^{2}}{\left[ Cu ^{2+}\right]}$
${\left[ Cu ^{2+}\right]=10^{-7} M }$
$x =7$
Answer: 216
Solution
$K = Ae e ^{- Ea / RT }=\left(6.5 \times 10^{12} s ^{-1}\right) e ^{-26000 K / T }$
$\frac{ Ea }{8.314}=26000$
$Ea =216.164 \,kJ / mol .$
Answer: 6
Solution
$Mn ^{2+} \rightarrow t _{2 g ^{111}} e _{ g ^{11}}$
$\mu_{ s }=\sqrt{35}$
$=5.91$
$=6$
JEE Main Mathematics Question Paper with Solution 2023 June 29th Shift 2 - Evening
A
1
B
$\alpha$
C
$1+\alpha$
D
$1+2 \alpha$
Solution
$x^{4}+x^{2}+1=0$
$\Rightarrow\left(x^{2}+x+1\right)\left(x^{2}-x+1\right)=0$
$\Rightarrow x=\pm \omega, \pm \omega^{2}$ where $\omega=1^{1 / 3}$ and imaginary.
So $\alpha^{1011}+\alpha^{2022}-\alpha^{3033}=1+1-1=1$
A
Exactly at one point
B
Exactly at two points
C
Nowhere
D
At infinitely many points.
Solution
A
-5
B
-6
C
-7
D
-8
Solution
$B =( I -\operatorname{adj} A )^{5}=\begin{bmatrix}-1 & -1 \\0 & -1\end{bmatrix}^{5}=\begin{bmatrix}-1 & -5 \\0 & -1\end{bmatrix}$
Sum of its all elements $=-7$.
A
$\frac{425}{216}$
B
$\frac{429}{216}$
C
$\frac{288}{125}$
D
$\frac{280}{125}$
Solution


$S = \frac{288}{125}$
A
$\frac{\pi^{2}}{6}$
B
$\frac{\pi^{2}}{3}$
C
$\frac{\pi^{2}}{2}$
D
$\pi^{2}$
Solution
$\displaystyle\lim _{x \rightarrow 1} \frac{\left(x^{2}-1\right) \sin ^{2} \pi x}{\left(x^{2}-1\right)(x-1)^{2}}=\displaystyle\lim _{x \rightarrow 1}\left(\frac{\sin ((1-x) \pi))}{\pi(1-x)}\right)^{2} \pi^{2}=\pi^{2}$
A
For $n _{1}=3, n _{2}=4$, there exists $\alpha \in(3,5)$ where $f$ attains local maxima.
B
For $n _{1}=4, n _{2}=3$, there exists $\alpha \in(3,5)$ where $f$ attains local manima.
C
For $n _{1}=3, n _{2}=5$, there exists $\alpha \in(3,5)$ where $f$ attains local maxima.
D
For $n _{1}=4, n _{2}=6$, there exists $\alpha \in(3,5)$ where $f$ attains local maxima.
Solution
$f^{\prime}(x)=(x-3)^{n_{1}-1}(x-5)^{n_{2}-1}\left(n_{1}+n_{2}\right)\left(x-\frac{5 n_{1}+3 n_{2}}{n_{1}+n_{2}}\right)$
Option (3) is incorrect since
for $n _{1}=3, n _{2}=5$
$f^{\prime}(x)=8(x-3)^{2}(x-5)^{4}\left(x-\frac{30}{8}\right)$
minima at $x=\frac{30}{8}$
A
(2, 4)
B
(1, 2)
C
(4, 17)
D
(6, 8)
Solution
$f(x)=\left(1+\int\limits_{0}^{1} f(t) d t\right) x-\int\limits_{0}^{1} tf ( t ) dt$
$f(x)=A x-B .....$ (i)
$A=1+\int\limits_{0}^{1} f(t) d t=1+\int\limits_{0}^{1}( At - B ) dt$
$\Rightarrow A =2(1- B ) .....$(ii)
Also $B =\int\limits_{0}^{1} tf ( t ) dt =\int\limits_{0}^{1}\left( At { }^{2}- Bt \right) dt$
$A =\frac{9}{2} B.....$(iii)
From $(2),(3)$
$A =\frac{18}{13}, B =\frac{4}{13}$
so $f(6) =8$
A
$\int\limits_{0}^{1}\left(1+\sqrt{1- y ^{2}}\right) d y$
B
$\int\limits_{0}^{1}\left(\frac{y^{2}}{2}-\sqrt{1-y^{2}}+1\right) d y$
C
$\int\limits_{0}^{1}\left(1-\sqrt{1-y^{2}}\right) d y$
D
$\int\limits_{0}^{1}\left(\frac{y^{2}}{2}+\sqrt{1-y^{2}}+1\right) d y$
Solution
$LHS =\int\limits_{0}^{2}\left(\sqrt{2 x}-\sqrt{2 x-x^{2}}\right) d x=\frac{8}{3}-\frac{\pi}{2}$
$R H S=\int\limits_{0}^{1}\left(1-\sqrt{1-y^{2}}-\frac{y^{2}}{2}\right) d y+\int\limits_{1}^{2}\left(2-\frac{y^{2}}{2}\right) d y+I$
$I+\frac{5}{3}-\frac{\pi}{4}$
So, $I=1-\frac{\pi}{4}=\int\limits_{0}^{1}\left(1-\sqrt{1-y^{2}}\right) d y$
A
2
B
-2
C
-4
D
-1
Solution
$\frac{d y}{1+y^{2}}+\frac{2 e^{x}}{1+e^{2 x}} d x=0....$(i)
on integration
$\tan ^{-1} y+2 \tan ^{-1} e^{x}=c$
$y(0)=0$
so, $C=\frac{\pi}{2} \Rightarrow \tan ^{-1} y+2 \tan ^{-1} e^{x}=\frac{\pi}{4}$
from eq.(i), $\left(\frac{d y}{d x}\right)_{x=0}=-1$
$\arg y (\ln \sqrt{3})=-\frac{1}{\sqrt{3}}$
$6\left[ y ^{\prime}(0)+\left( y (\ln \sqrt{3})^{2}\right]=6\left[-1+\frac{1}{3}\right]=-4\right.$
A
8 only
B
2 only
C
$\frac{1}{4}$ only
D
any a $>0$
Solution
Lines making angle $\frac{\pi}{4}$ with $y=3 x+5$ have slope $-2 \& 1 / 2$.
Which are perpendicular to each-other so, $A, S, B$ are collinear for all $a >0$.

A
$(\sqrt{2}+\sqrt{6}) / 3$
B
$(\sqrt{6}+\sqrt{3}) / 2$
C
$(3+\sqrt{3}) / 4$
D
None of the above
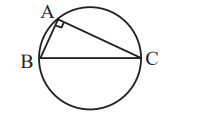
Solution
Radius of given circle is $1 .$
$ BC =$ diameter $=2, AB =\sqrt{2}$
$ AC =\sqrt{ BC ^{2}- AB ^{2}}=\sqrt{2} $
$\triangle ABC =\frac{1}{2} AB \cdot AC =1$
A
$\sqrt{\frac{3}{109}}$
B
$\sqrt{\frac{5}{142}}$
C
$\sqrt{\frac{5}{71}}$
D
$\sqrt{\frac{1}{142}}$
Solution
$(2, -1,-3)$ satisfy the given plane.
So $2 p + q =8$
Also given line is perpendicular to normal plane so
$3 p+2 q-1=0$
$\Rightarrow p =15, q =-22$
Eq. of plane $15 x-22 y+z-5=0$
its distance from origin $=\frac{6}{\sqrt{710}}=\sqrt{\frac{5}{142}}$
A
$\sqrt{2}$
B
2
C
$2 \sqrt{2}$
D
4
Solution
$AB \equiv x -2 y +1=0$
$AC \equiv 2 x - y -1=0$
So $A (1,1)$
Altitude from $B$ is $BH = x +2 y -7=0 \Rightarrow B (3,2)$
Altitude from $C$ is $CH =2 x + y -7=0 \Rightarrow C (2,3)$
Centroid of $\triangle ABC = E (2,2) OE =2 \sqrt{2}$
A
$(2,1,0)$
B
$(1,2,1)$
C
$(1,2,2)$
D
$(1,3,2)$
Solution
Image of $P (1,2,1)$ in $x +2 y +2 z -16=0$
is given by $Q (4,8,7)$
Eq. of plane $T =\begin{vmatrix} x & y & z +1 \\ 4 & 8 & 6 \\ 1 & 1 & 2\end{vmatrix}=0$
$\Rightarrow 2 x - z =1$ so $B (1,2,1)$ lies on it.
A
$\frac{\sqrt{82}}{2}$
B
$\frac{\sqrt{62}}{2}$
C
$\frac{\sqrt{69}}{2}$
D
$\frac{\sqrt{66}}{2}$
Solution
$\overrightarrow{AB} || \overrightarrow{AC}$ if $\frac{1}{2}=\frac{\alpha-4}{-6}=\frac{1}{2} \Rightarrow \alpha=1$
$\vec{a} , \vec{b} , \vec{c}$ are non-collinear for $\alpha=2$ (smallest positive integer)
Mid-point of $BC = M \left(\frac{5}{2}, 0, \frac{9}{2}\right)$
$AM =\sqrt{\frac{9}{4}+16+\frac{9}{4}}=\frac{\sqrt{82}}{2}$
A
$\frac{5}{16}$
B
$\frac{9}{16}$
C
$\frac{11}{16}$
D
$\frac{13}{16}$
Solution
Total no. of relations $=2^{2 \times 2}=16$
Fav. relation $=\phi,\{( x , x )\},\{( y , y )\},\{( x , x )( y , y )\}$
$\{(x, x),(y, y),(x, y)(y, x)\}$
Prob. $=\frac{5}{16}$
A
0
B
2
C
5
D
infinite
Solution
Mean $=13$
Variance $=\frac{9+49+144+ a ^{2}+(43- a )^{2}}{5}-13^{2} \in N$
$\Rightarrow \frac{2 a^{2}-a+1}{5} \in N$
$\Rightarrow 2 a ^{2}- a +1-5 n =0$ must have solution as natural numbers
its $D=40 n-7$ always has $3$ at unit place
$\Rightarrow D$ can't be perfect square
So, a can't be integer.
A
$15 \sqrt{3}$
B
$20 \sqrt{3}$
C
$20+10 \sqrt{3}$
D
$30$
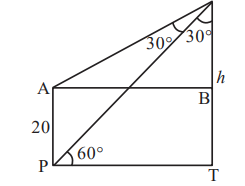
Solution
$PT =\frac{ h }{\sqrt{3}}= AB$
$\frac{ AB }{ h -20}=\sqrt{3}$
$h =3( h -20)$
$h =30$
A
$p \wedge(\sim q ) \wedge r$
B
$(\sim p ) \wedge(\sim q ) \wedge r$
C
$(\sim p) \wedge q \wedge r$
D
$p \wedge q \wedge(\sim r )$
Solution
$ P \vee q \Rightarrow(\sim r \vee p )$
$\equiv \sim( p \vee q ) \vee(\sim r \vee p ) $
$\equiv(\sim p \wedge \sim q ) \vee( p \vee \sim r )$
$\equiv[\sim p \vee p ) \wedge(\sim q \vee p )] \vee \sim r$
$\equiv[\sim q \vee p ) \vee \sim r$
Its negation is $\sim p \wedge q \wedge r$
A
$1+{ }^{n} C_{2}(8-5)+{ }^{n} C_{3}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-1}-5^{n-}\right.$ 1)
B
$1+{ }^{n} C_{3}(8-5)+{ }^{n} C_{4}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-2}-5^{n-}\right.$ 2)
C
${ }^{ n } C _{3}(8-5)+{ }^{ n } C _{4}\left(8^{2}-5^{2}\right)+\ldots+{ }^{ n } C _{ n }\left(8^{ n -2}-5^{ n -2}\right)$
D
${ }^{n} C_{4}(8-5)+{ }^{n} C_{5}\left(8^{2}-5^{2}\right)+\ldots+{ }^{n} C_{n}\left(8^{n-3}-5^{n-3}\right)$
Solution
$\alpha=\frac{(1+8)^{ n }-8 n -1}{64}={ }^{ n } C _{2}+{ }^{ n } C _{3} 8+{ }^{ n } C _{4} 8^{2}+\ldots$
$\beta={ }^{n} C_{2}+{ }^{n} C_{3} 5+{ }^{n} C_{4} 5^{2}+\ldots$
option (3) will be the answer.
Answer: 0
Solution
$ \vec{a} + \vec{b} \times \vec{c} =0 $
$ \vec{a} \times \vec{b} +| \vec{b} |^{2} \vec{c} -5 \vec{b} =0$
It gives $\vec{c}=\frac{1}{3}(10 \hat{i}+3 \hat{ j }+2 \hat{ k })$
so $3 \vec{a}. \vec{c} =10$
But it does not satisfy $\vec{a} + \vec{b} \times \vec{c} =0$.
This question has data error.
Alternate (Explanation) :
According to given $a$ & $b$
$a \cdot b =1-2+3=2 \ldots$ (i)
but given equation
$\vec{a} =-( \vec{b} \times \vec{c} )$
$\Rightarrow \vec{a} \perp \vec{b} \Rightarrow \vec{a} \cdot \vec{b} =0$
which contradicts.
Answer: 14
Solution
$\frac{ dy }{ dx }+\frac{2 x }{ x -1} \cdot y =\frac{1}{( x -1)^{2}}$
$y =\frac{1}{( x -1)^{2}}\left[\frac{ e ^{2 x }+1}{2 e ^{2 x }}\right]$
$y (3)=\frac{ e ^{6}+1}{8 e ^{6}}$
$\alpha+\beta=14$
Answer: 2223
Solution
For series of common terms
$a =9, d =12, n =19$
$S_{19}=\frac{19}{2}[2(9)+18(12)]=2223$
Answer: 4
Solution
$\sin ^{2} x+\sin x-1=0$
$\sin x=\frac{-1+\sqrt{5}}{2}=+v e$
Only $4$ roots
Answer: 12
Solution
given $\pi a ^{2}-\pi ab =30 \pi$ and $\pi ab -\pi b ^{2}=18 \pi$
on subtracting, we get $(a-b)^{2}=a^{2}-2 a b+b^{2}=12$
Answer: 4
Solution
Let $h(x)=f(x) g^{\prime}(x) \rightarrow 5$ roots
$f ( x )$ is even $\Rightarrow$
$f \left(\frac{1}{4}\right)= f \left(\frac{1}{2}\right)= f \left(-\frac{1}{2}\right)= f \left(\frac{1}{4}\right)=0$
$g ( x )$ is even $\Rightarrow g \left(\frac{3}{4}\right)= g \left(-\frac{3}{4}\right)=0$
$g ^{\prime}( x )=0$ has minimum one root
$h^{\prime}( x )$ has at last $4$ roots
Answer: 5
Solution
$T _{ r +1}=(-1)^{ r } \cdot{ }^{15} C _{ r } \cdot 2^{15- r } \times \frac{15-2 r }{5}$
$m ={ }^{15} C _{10} 2^{5}$
$n =-1$
so $mn ^{2}={ }^{15} C _{5} 2^{5}$
Answer: 1086
Solution
Let the number is $abcd$, where $a,b,c$ are divisible by $d$.
No. of such numbers
$d = 1$
$9 \times 10 \times 10=900$
$d = 2$
$4 \times 5 \times 5=100$
$d = 3$
$3 \times 4 \times 4=48$
$d = 4$
$2 \times 3 \times 3 =18$
$d = 5$
$1 \times 2 \times 2 =4$
$d = 6, 7, 8, 9$
$4 \times 4 = 16$
$1086$
| No. of such numbers | |
|---|---|
| $d = 1$ | $9 \times 10 \times 10=900$ |
| $d = 2$ | $4 \times 5 \times 5=100$ |
| $d = 3$ | $3 \times 4 \times 4=48$ |
| $d = 4$ | $2 \times 3 \times 3 =18$ |
| $d = 5$ | $1 \times 2 \times 2 =4$ |
| $d = 6, 7, 8, 9$ | $4 \times 4 = 16$ |
| $1086$ |
Answer: 1
Solution
$M =\begin{bmatrix}0 & -\alpha \\ \alpha & 0\end{bmatrix} ; M ^{2}=\begin{bmatrix}-\alpha^{2} & 0 \\ 0 & -\alpha^{2}\end{bmatrix}=-\alpha^{2} I$
$N = M ^{2}+ M ^{4}+\ldots \ldots+ M ^{98}=\left[-\alpha^{2}+\alpha^{4}-\alpha^{6}+\ldots\right] I$
$=-\alpha^{2} \frac{\left(1-\left(-\alpha^{2}\right)^{49}\right)}{1+\alpha^{2}} . I$
$I - M ^{2}=\left(1+\alpha^{2}\right) I$
$\left( I - M ^{2}\right) N =-\alpha^{2}\left(\alpha^{98}+1\right)=-2$
$\alpha=1$
Answer: 18