JEE Main Physics Question Paper with Solution 2022 June 29th Shift 1 - Morning
A
10
B
15
C
20
D
30
Solution
Let they meet at time $t$.
$t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 80}{10}} $
$=4\, \sec$
Time taken by ball $B$ to meet $A =2 \,\sec$
using $ S=u t+\frac{1}{2} at ^{2}$
$-80=- u \times 2+\frac{1}{2}(-10)(2)^{2} $
$ u =30$
A
$15 \,ms ^{-1}$
B
$25 \,ms ^{-1}$
C
$35 \,ms ^{-1}$
D
$50 \,ms ^{-1}$
Solution
Mass of pieces by $\frac{M}{4}, \frac{M}{4}, \frac{M}{2}$
conserving momentum
$\overrightarrow{ P }_{1}+\overrightarrow{ P }_{2}+\overrightarrow{ P }_{3}=0$
$\overline{ P }_{3}=-\left(\overline{ P }_{1}+\overline{ P }_{2}\right)$
As $\overline{ P }_{1} \& \overline{ P }_{2}$ are perpendicular
so $P _{3}=\sqrt{ P _{1}^{2}+ P _{2}^{2}}$
$P _{3}=(50) \frac{ M }{4}$
$\& P _{3}=\frac{ M }{2} V$
so $v=25$
A
30 days
B
35 days
C
40 days
D
25 days
Solution
$\frac{ A }{ A _{0}}=\frac{ N }{ N _{0}}$
$\frac{2 \times 10^{-5}}{2.56 \times 10^{-3}}=\frac{ N }{ N _{0}} $
$\frac{ N }{ N _{0}}=\frac{1}{128} \Rightarrow N =\frac{ N _{0}}{128}$
After $7$ half life activity comes down to given value $T =7 \times 5$
$=35 $ days
A
2
B
3
C
5
D
4
Solution
$L _{0}=$ angular momentum of shell about $O$.
As shell is rolling
so $ V _{ cm }=\omega R $
$ L _{0}= mV _{ cm } R + I \omega $
$=1 \times \omega R \times R +\frac{2}{3} R ^{2} \omega$
$=\frac{5}{3} R ^{2} \omega $
so $ a =5$
A
249 J
B
415 J
C
498 J
D
830 J
Solution
No of moles $=\frac{44.8}{22.4}=2$
Gas is mono atomic so $C _{ v }=\frac{3}{2} R$
$\Delta Q = nC _{ v } \Delta T $
$=2 \times \frac{3}{2} R (20) $
$=60 \,R$
$=60 \times 8.3 $
$=498\, J$
A
$\sqrt{ L _{1} L _{2}}$
B
$\frac{ L _{1}+ L _{2}}{2}$
C
$2 L _{1}- L _{2}$
D
$3 L_{1}-2 L_{2}$
Solution
By Hooke's Law
so $F \alpha \Delta L$
$\frac{ F _{1}}{ F _{2}}=\frac{\Delta L _{1}}{\Delta L _{2}}$
$\frac{10}{20}=\frac{\left( L _{1}- L \right)}{\left( L _{2}- L \right)}$
$L =2 L _{1}- L _{2}$
A
Both A and R are correct and R is the correct explanation of A
B
Both A and R are correct but R is not the correct explanation of A
C
A is correct but R is not correct
D
A is not correct but R is correct
Solution
To free the electron from metal surface minimum energy required, is equal to the work function of that metal.
So Assertion $A$, is correct.
$h v = w _{0}+ K . E _{\max }$
if $hv = w _{0}$
$\Rightarrow \text { K.E. }_{\max }=0$
Hence reason $R$, is correct, But $R$ is not the correct explanation of $A$.
A
2 J
B
4 J
C
8 J
D
16 J
Solution
By work energy theorem
work done by net force $=\Delta K$.E.
$\Rightarrow W =\frac{1}{2} mu _{ f }^{2}-\frac{1}{2} mu _{ i }^{2} $
$ w =\frac{1}{2} \times 0.5 \times(0.25)^{2} \times(4)^{5} $
$ w =16\, J $
A
$1: 1$
B
$1: 2$
C
$2:1$
D
$1: 4$
Solution
radius of paerticle in cyclotron
$r=\frac{\sqrt{2 mK \cdot E .}}{ qB }$
So ratio of new radius to original
$\frac{r_{n}}{r_{0}}=\sqrt{\frac{(\text { K.E. })_{n}}{(\text { K.E })_{0}}}$
$=\sqrt{4} \Rightarrow 2: 1$
A
(a) and (d) only
B
(b) and (d) only
C
(a) and (c) only
D
(b) and (c) only
Solution
at $ \omega_{ r }, X _{ C }= X _{ L } $
$\Rightarrow \frac{1}{\omega_{ r } C }=\omega_{ r } L$
So if $\omega < \omega_{ r }$ then $x _{ C }$ will increase and $X _{ L }$ will decrease.
Hence to left of $\omega_{ r }$ circuit is capacitive
$Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}$
at $\omega_{r}, Z=\sqrt{R^{2}+O^{2}}=R(C)$
A
3
B
6
C
5
D
4
Solution
$F =\frac{ dp }{ dt }=v \frac{ dm }{ dt }$
$\Rightarrow Ma =10 \times 1$
$\Rightarrow 2 a =10$
$a =5\, m / sec ^{2}$
A
$\frac{P}{V}$
B
$\frac{ V }{ P }$
C
PV
D
$PV ^{3}$
Solution
By principle of homogenity
${[ P ]=\left[\frac{ a }{ v ^{2}}\right] \text { and }[ b ]=[ v ]}$
$\Rightarrow\left[\frac{ a }{ b }\right]=[ PV ]( C )$
A
$\sin ^{-1}\left(\frac{3}{5}\right)$
B
$\sin ^{-1}\left(\frac{1}{3}\right)$
C
$\cos ^{-1}\left(\frac{3}{5}\right)$
D
$\cos ^{-1}\left(\frac{1}{3}\right)$
Solution
$\left(a^{2}+b^{2}+2 a b \cos \theta\right)=4\left(a^{2}+b^{2}-2 a b \cos \theta\right)$
put $a=b$ we get
$2 a^{2}+2 a^{2} \cos \theta=8 a^{2}-8 a^{2} \cos \theta$
$\cos \theta=\frac{3}{5}$
A
$12 \, kms ^{-1}$
B
$24 \, kms ^{-1}$
C
$36 \, kms ^{-1}$
D
$6 \, kms ^{-1}$
Solution
$ V _{\text {escape }}=\sqrt{\frac{2 Gm }{ R }} $
$\Rightarrow \sqrt{\frac{2 G \rho \times \frac{4}{3} \pi R ^{3}}{ R }}$
$ V _{\text {escape }} \propto \sqrt{\rho R ^{2}}$
$\therefore$ if $\rho$ is $4$ times and Radius is halved.
$\Rightarrow V _{\text {escape }} $ will remain same
A
$\frac{1}{\sqrt{3}}$
B
$\frac{1}{2}$
C
$\sqrt{3}$
D
$1$
Solution
$B _{ H }= B \cos \theta$
$\therefore B =\frac{ B _{ H }}{\cos \theta}=\frac{0.5 G }{\cos 30^{\circ}} \Rightarrow \frac{ G }{\sqrt{3}}$
A
$2 \pi$
B
$5 \pi$
C
$\pi$
D
$\frac{5 \pi}{2}$
Solution
$V _{ P } \max =4 V _{\text {wave }}$
$\omega A =4\left(\frac{\omega}{ k }\right) $
$\Rightarrow A =\frac{4 \lambda}{2 \pi}$
$\lambda=\frac{2 \pi A }{4}$
$ \Rightarrow \frac{20 \pi}{4} $
$\Rightarrow 5 \pi$
A
increase by $50 \%$
B
decrease by $15 \%$
C
increase by $25 \%$
D
increase by $33 \%$
Solution
$E \Rightarrow \frac{1}{2}( KC ) v ^{2}$
$\therefore \%$ change
$\Rightarrow \frac{\frac{1}{2} K _{2} CV ^{2}-\frac{1}{2} K _{1} CV ^{2}}{\frac{1}{2} K _{1} CV ^{2}}$
$=\frac{ K _{2}- K _{1}}{ K _{1}} \times 100$
$\Rightarrow \frac{15-10}{10} \times 100=50 \%$
A
1 m
B
5 m
C
10 m
D
0.5 m
Solution
Distance travelled by particle before stopping
$\frac{ V ^{2}}{2 a }= S \Rightarrow \frac{ v ^{2} m }{2 qE }$
$ \Rightarrow \frac{(200)^{2} \times 100 \times 10^{-6}}{2 \times 40 \times 10^{-6} \times 10^{5}}=0.5 \,m$
A
0.5 mm
B
1.0 mm
C
0.6 mm
D
0.3 mm
Solution
Fringe width $\beta=\frac{ D \lambda}{ d }$
$\lambda_{1}=5000 \,\mathring{A} $
$\beta_{1}=\frac{ D }{ d }\left(5000 \times 10^{-10}\right)=5 \times 10^{-4} m \ldots $ (I)
$\beta_{2}=\frac{ D }{(2 d )}\left(6000 \times 10^{-10}\right)= x $ (let) ...(II)
Divide (II) & (I)
$\frac{\beta_{2}}{\beta_{1}}=\frac{3000 \times 10^{-10}}{5000 \times 10^{-10}}=\frac{ x }{5 \times 10^{-4}} $
$ x =3 \times 10^{-4} m $ or $ 0.3\, mm$
A
$375 \times 10^{7}$
B
$75 \times 10^{7}$
C
$375 \times 10^{8}$
D
$75 \times 10^{9}$
Solution
Frequency at $1000\, nm =\frac{3 \times 10}{1000 \times 10^{-9}} $
$\Rightarrow 3 \times 10^{14} Hz$ available for channel band width
$=\frac{2}{100} \times 3 \times 10^{14}$
$ \Rightarrow 6 \times 10^{12} Hz$
Bandwidth for 1 channel $=8000\, Hz$
$\therefore$ No. of channel
$=\frac{6 \times 10^{12}}{8 \times 10^{3}}$
$ \Rightarrow \frac{600}{8} \times 10^{7}=75 \times 10^{7}$
Answer: 15
Solution
$\frac{ dQ }{ dt }= i ^{2} R =\frac{ V ^{2}}{ R } $ (we know)
$\Rightarrow $ In '$t$' time, $ \Delta Q=\left(\frac{ V ^{2}}{ R }\right) t$
Given that, (for same source, $v=$ same)
$ Q _{0}=\frac{ v ^{2}}{ R _{1}} \times 20=\frac{ V ^{2}}{ R _{2}} \times 60 \ldots \ldots$ (1)
$\Rightarrow R _{2}=3 R _{1} \ldots \ldots $ (ii)
If they are connected in parallel then
Req $=\frac{ R _{2} R _{1}}{ R _{1}+ R _{2}}=\frac{3 R _{1} \cdot R _{1}}{3 R _{1}+ R _{1}}=\left(\frac{3 R _{1}}{4}\right)$
To produce same heat, using equation ...(1)
$Q _{0}=\frac{ V ^{2}}{ R _{1}} \times 20=\frac{ v ^{2}}{\left(\frac{3 R _{1}}{4}\right)} \times t$
$t =\frac{3 \times 20}{4}=15 \,\min$
Answer: 43
Solution
$I =\left(\frac{1}{2} \varepsilon_{0} E _{0}^{2}\right) C$
$\Rightarrow E _{0} \Rightarrow \sqrt{\frac{2 I }{\varepsilon_{0} C }}$
$ \Rightarrow \sqrt{\frac{2 \times 0.22}{8.85 \times 10^{-12} \times 3 \times 10^{8}}}=12.873$
$B \Rightarrow \frac{ E _{0}}{ C } \Rightarrow \frac{12.873}{3 \times 10^{8}}$
$=4.291 \times 10^{-8}=43 \times 10^{-9}$
Answer: 21
Solution

$\frac{\Delta Q }{\Delta t }=\left(\frac{1}{ R }\right) \Delta T$
$R$ : Thermal resistivity
$\therefore R _{1}=\frac{ L _{1}}{ K _{1} A }=\frac{ L _{1}}{ K (120)} $
$ L _{1}=4\, cm$
$A =120\, cm ^{2}$
$ R _{2}=\frac{2.5}{(2 K )(120)}$
Now, $R _{ eq }$ of this series combination
$R_{ eq }= R _{1}+ R _{2}$
where $L _{ eq }=4+2.5=6.5$
$\frac{ L _{ eq }}{ K _{ eq }( A )}=\frac{4}{ K (120)}+\frac{5}{\frac{2}{2 K (120)}}$
$\frac{6.5}{ K _{ eq }(120)}=\frac{4}{ K (120)}+\frac{5}{4 K (120)}$
$\frac{6.5}{ K _{ eq }}=\frac{21}{4 K }$
$K _{ cq }=\frac{26}{21} K =\left(1+\frac{5}{21}\right) K$
$\therefore a=21$
Answer: 700
Solution
$A =10\, cm$
$\therefore$ Total Energy $=\frac{1}{2} KA ^{2}$
By energy conservation we can final $v$ at $x=5$
$\frac{1}{2} K (10)^{2}=\frac{1}{2} K (5)^{2}+\frac{1}{2} mv ^{2}$
$ V =\sqrt{\frac{75 \,K }{ m }}$
Now, velocity is tripled through external mean so the amplitude of SHM will charge and so the total energy, (but potential) energy at this moment will remain same)
$\therefore \frac{1}{2} K (5)^{2}+\frac{1}{2} m \left(3 \sqrt{\frac{75\, K }{ m }}\right)^{2}=\frac{1}{2} KA ^{2}$
$\Rightarrow 25 \,K +675\, K = KA ^{2}$
$\therefore A =\sqrt{700}$
$\therefore x =700$
Answer: 144
Solution
$1=\rho \frac{\ell}{ A }$
$1=\frac{\rho \times 31.4}{\frac{\pi(2.4)^{2}}{4}}$
$\frac{\pi(2.4)^{2}}{4}=\rho \times 314$
$\frac{2.4 \times 2.4}{4}=\rho \times 10$
$\frac{0.6 \times 2.4}{10}=\rho$
$\frac{1.44}{10}=\rho$
$0.144=\rho$
$144 \times 10^{-3}=\rho$
Answer: 102
Solution
$1-\frac{ Q _{2}}{ Q _{1}}=1-\frac{ T _{2}}{ T _{1}}$
$\frac{ Q _{2}}{ Q _{1}}=\frac{ T _{2}}{ T _{1}}$
$\frac{225}{300}=\frac{ T _{2}}{500}$
$\frac{500 \times 225}{300}= T _{2}$
$375= T _{2}$
$102^{\circ} C = T _{2}$
Answer: 3
Solution
$\sqrt{ d } \propto \cot \frac{\theta}{2}$
$\cot ^{2} 30^{\circ}=x \cot ^{2} 45^{\circ}$
$3=x$
Answer: 2
Solution
$\Delta i _{ B }=100 \,\mu A $
$\beta=\frac{\Delta i _{ C }}{\Delta i _{ B }}$
$\Delta i _{ C }=10\, mA$
power $=\beta^{2} \times \frac{ R _{0}}{ R _{ in }}$
Power $=\left(\frac{10}{0.1}\right)^{2} \times \frac{2}{1}$
Power $=100 \times 100 \times 2$
Gain $=2 \times 10^{4}$
Answer: 225
Solution
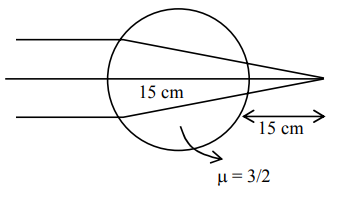
$\frac{\frac{3}{2}}{ V }-\frac{1}{\infty}=\frac{\frac{3}{2}-1}{15}$
$\frac{3}{2 V }=\frac{1}{30}$
$V =45 \,cm$
$\frac{1}{ V }-\frac{3}{\frac{2}{15}}=\frac{1-\frac{3}{2}}{\frac{2}{-15}}$
$\frac{1}{ V }-\frac{1}{10}=\frac{1}{30}$
$\frac{1}{ V }=\frac{1}{10}+\frac{1}{30}=\frac{4}{30}$
$V =7.5$
$V =22.5$
$V =225 \,mm$
Answer: 10
Solution

$i=\frac{15}{3}=5 A$
$15-5(1)=10$ Volt
JEE Main Chemistry Question Paper with Solution 2022 June 29th Shift 1 - Morning
A
1400
B
2200
C
3360
D
4200
Solution
Moles of $Fe _{3} O _{4}=\frac{4.640 \times 10^{3}}{232}=20$
Moles of $CO =\frac{2.52 \times 10^{3}}{28}=90$
So limiting Reagent $= Fe _{3} O _{4}$
So moles of $Fe$ formed $=60$
Weight of $Fe =60 \times 56=3360\, gms$
A
(A), (C) and (D) only
B
(A) and (B) only
C
(A) and (C) only
D
(A), (B) and (C) only
Solution
(A) $Cr =[ Ar ] 3 d ^{5} 4 s ^{1}$
(B) $m=-\ell$ to $+\ell$
(C) According to Aufbau principle, orbitals are filled in order of their increasing energies.
(D) Total nodes $= n -1$
A
(A) > (C) > (B) > (D)
B
(B) > (A) > (C) > (D)
C
(A) > (B) > (C) > (D)
D
(A) > (B) > (D) > (C)
Solution
$LiCl > NaCl > KCl > CsCl ($ Covalent character $)$
A
$0.01 \,M \,KCl$
B
$0.01 \,M\, HCl$
C
$0.01 \,M\, AgNO _{3}$
D
Deionised water
Solution
In deionized water no common ion effect will take place so maximum solubility
A
Brownian motion destabilises sols.
B
Any amount of dispersed phase can be added to emulsion without destabilising it.
C
Mixing two oppositely charged sols in equal amount neutralises charges and stabilises colloids.
D
Presence of equal and similar charges on colloidal particles provides stability to the colloidal solution
Solution
As equal & similar charge particle will repel each other, hence will never precipitate.
A
$[ Xe ] 4 f ^{14} 5 d ^{9} 6 s ^{1}$
B
$[ Kr ] 4 f ^{14} 5 d ^{10}$
C
$[ Xe ] 4 f ^{14} 5 d ^{10}$
D
$[ Xe ] 4 f ^{14} 5 d ^{8} 6 s ^{2}$
Solution
${ }_{78} Pt =[ Xe ] 4 f ^{44} 5 d ^{9} 6 s ^{1}$ (Exceptional electronic configuration)
A
Zinc
B
Gold
C
Silver
D
Copper
Solution
For $ZnS , KCN$ is used as depressant.
For Gold and silver $\Rightarrow$ leaching [Cyanide process]
A
$HOCl + H _{2} O _{2} \rightarrow H _{3} O ^{+}+ Cl ^{-}+ O _{2}$
B
$PbS +4 H _{2} O _{2} \rightarrow PbSO _{4}+4 H _{2} O$
C
$2 MnO _{4}^{-}+3 H _{2} O _{2} \rightarrow 2 MnO _{2}+3 O _{2}+2 H _{2} O +2 OH ^{-}$
D
$Mn ^{2+}+ H _{2} O _{2} \rightarrow Mn ^{4+}+2 OH ^{-}$
Solution
In option (A) and $(C)$ reducing action of hydrogen peroxide is shown.
In option (A) it is in acidic medium, in option (B) it is in basic medium. or
For reducing ability $H _{2} O _{2}$ changes to $O _{2}$, i.e. oxidize, so in option ' $A ^{\prime} \& C ^{\prime} O _{2}$ is formed but ' $A$ ' is in acidic medium so option - $C$ correct.
A
(A)-(I), (B)-(II), (C)-(III), (D)-(IV)
B
(A)-(III), (B)-(II), (C)-(I), (D)-(IV)
C
(A)-(III), (B)-(I), (C)-(II), (D)-(IV)
D
(A)-(IV), (B)-(II), (C)-(I), (D)-(III)

A
(A)-(III), (B)-(I), (C)-(IV), (D)-(II)
B
(A)-(IV), (B)-(III), (C)-(II), (D)-(I)
C
(A)-(II), (B)-(III), (C)-(IV), (D)-(I)
D
(A)-(I), (B)-(IV), (C)-(II), (D)-(III)
Solution
Caesium is used in devising photoelectric cells.
Boron fibres are used in making bullet-proof vest.
Silicones being surrounded by non-polar alkyl groups are water repelling in nature.
Gallium is less toxic and has a very high boiling point, so it is used in high temperature thermometers.
A
Phosphonic acid
B
Phosphinic acid
C
Pyrophosphorus acid
D
Hypophosphoric acid
Solution
$P _{4}+3 NaOH +3 H _{2} O \rightarrow PH _{3}+3 NaH _{2} PO _{2}$
oxoacid $= H _{3} PO _{2}$ (hypo phosphorus acid) or (phosphinic acid)
A
Sulfuric acid
B
Hydrofluoric acid
C
Phosphoric acid
D
Hydrochloric acid
Solution
$CaCO _{3}+ H _{2} SO _{4} \rightarrow CaSO _{4}+ H _{2} O + CO _{2}$
A
But-1-ene
B
cis-But-2-ene
C
trans-But-2ene
D
2-methyl propene

A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are incorrect.
C
Statement I is correct but Statement II is incorrect.
D
Statement I is incorrect but Statement II is correct.
Solution

electron with drawing group on carboxylic acid
will increase the rate of esterification
A
Bakelite
B
Nylon 6,6
C
Buna-N
D
Terylene
Solution
Buna - N is synthetic rubber which can be stretched and retains its original status on releasing the force.
A
$\beta$-D-2-deoxyribose, $\beta$-D-deoxyribose
B
$\beta$-D-2-deoxyribose, $\beta$-D-ribose
C
$\beta$-D-ribose, $\beta$-D-2-deoxyribose
D
$\beta$-D-deoxyribose, $\beta$-D-2-deoxyribose
Solution
DNA contains $\Rightarrow \beta-D-2-$ deoxyribose
RNA contains $\Rightarrow \beta- D -$ ribose
A
Cimetidine
B
Ranitidine
C
Histamine
D
Saccharin
Solution

Histamine is nitrogenous compound it does not contain sulpher.
A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are incorrect.
C
Statement I is correct but Statement II is incorrect.
D
Statement I is incorrect but Statement II is correct.
Solution
Phenol are weakly acidic. Phenol is more acidic than alcohol \& $H _{2} O$ statement (I) is correct. (II) is incorrect.
Answer: 152
Solution
Assuming ideal behaviour $P =\frac{ dRT }{ M }$
$P =\frac{100}{760} atm , T =257+273=530 K$
$d =0.46 \,gm / L$
So $M =\frac{0.46 \times 0.082 \times 530}{100} \times 760$
$=151.93 \approx 152$
Answer: 117
Solution
Given data is for 1 moles and asked for 5 moles so value is $23.4 \times 5=117 kJ$
Answer: 5
Solution
$M = d \times V =1.02 \times 1.2=1.224 gm$
Moles of acetic acid $=0.0204$ moles in $2 L$
So molality $=0.0102 mol / kg$
Now $\Delta T _{ f }= i \times K _{ f } \times M$
$i=1+\alpha$ for acetic acid
$0.0198=(1+\alpha) \times 1.85 \times 0.0102 $
$\alpha=0.04928 $
$\cong 5 \%$
Answer: 127
Solution
At anode
$2 H _{2} O \rightarrow O _{2}( g )+4 H ^{+}+4 e ^{-}$
At cathode
$2 H ^{+}+2 e ^{-} \rightarrow H _{2}( g )$
Now number of gm eq. $=\frac{ i \times t }{96500}$
$=\frac{0.1 \times 2 \times 60 \times 60}{96500} $
$=0.00746$
$ V _{ O _{2}}=\frac{0.00746}{4} \times 22.7=0.0423$
$ V _{ H _{2}}=\frac{0.00746}{2} \times 22.7=0.0846$
$ V _{\text {Total }} \approx 127 ml \text { or } cc$
Answer: 1
Solution
$ln \left(\frac{ K _{2}}{ K _{1}}\right)=\frac{ E _{ a }}{ R }\left(\frac{1}{ T _{1}}-\frac{1}{ T _{2}}\right)$
$ln \left(\frac{ K _{2}}{ K _{1}}\right)=\frac{532611}{8.3} \times\left(\frac{10}{310 \times 300}\right)$
where $K _{2}$ is at $310 K \& K _{1}$ is at $300\, K$
$ln \left(\frac{ K _{2}}{ K _{1}}\right)=6.9$
$= 3 \times \ell n 10 $
$ln \frac{ K _{2}}{ K _{1}}= ln 10^{3} $
$K _{2}= K _{1} \times 10^{3}$
$K _{1}= K _{2} \times 10^{3}$
So, $K = 1$
Answer: 0
Solution
$3 MnO _{4}^{2-}+4 H ^{+} \longrightarrow 2 \overset{+}{Mn}O _{4}^{-}+ \overset{+4}{Mn}O _{2}+2 H _{2} O$
$Mn ^{+7}=$ no. of unpaired electrons is ' $0$ '
$\mu=0 \text { B.M. }$
Answer: 64
Solution
Meq of $ H _{2} SO _{4} $ used by $ NH _{3}=12.5 \times 1 \times 2=25$
$\%$ of $N$ in the compound $=\frac{25 \times 10^{-3} \times 14 \times 100}{0.55}=63.6$ or
Meq. of $H _{2} SO _{4}=$ Meq. of $NH _{3}$
12. $5 \times 1 \times 2=25$ meq. of $NH _{3}$
$=25$ millimoles of $NH _{3}$
So Millimoles of ' $N$ ' $=25$
Moles of ' $N ^{\prime}=25 \times 10^{-3}$
wt. of $N =14 \times 25 \times 10^{-3}$
$\% N =\frac{14 \times 25 \times 10^{-3}}{0.55} \times 100$
$=63.66 $
$\approx 64 \%$
Answer: 3
Solution

Number of compounds containing asymmetric carbons are three.
Answer: 1
Solution

no. of carbon atoms present in $B$ is $1$
JEE Main Mathematics Question Paper with Solution 2022 June 29th Shift 1 - Morning
A
$\frac{133}{10^{4}}$
B
$\frac{18}{10^{3}}$
C
$\frac{19}{10^{3}}$
D
$\frac{271}{10^{4}}$
Solution
Let matrix $A$ is singular then $| A |=0$
Number of singular matrix $=$ All entries are same $+$ only two prime number are used in matrix
$=10+10 \times 9 \times 2 $
$=190$
Required probability $=\frac{190}{10^{4}}=\frac{19}{10^{3}}$
A
15
B
11
C
13
D
17
Solution
$y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}$
$\Rightarrow x \frac{d v}{d x}=\sqrt{v^{2}+16}$
$\Rightarrow \int \frac{d v}{\sqrt{v^{2}+16}}=\int \frac{d x}{x}$
$\Rightarrow \ln \left|v+\sqrt{v^{2}+16}\right|=\ln x+\ln C$
$\Rightarrow y+\sqrt{y^{2}+16 x^{2}}=C x^{2}$
As $y(1)=3 \Rightarrow C=8$
$\Rightarrow y(2)=15$
A
54
B
50
C
-6
D
-42
Solution
$\frac{a-2}{3}=\frac{b-4}{-1}=\frac{c-7}{4}=\frac{-2(6-4+28-2)}{3^{2}+1^{2}+4^{2}}$
$\Rightarrow a=\frac{-84}{13}+2, b=\frac{28}{13}+4, C=\frac{-112}{13}+7$
$\Rightarrow 2 a+b+2 c=-6$
A
$\left(3, \frac{27}{4}\right)$
B
$\left(3, \frac{23}{4}\right)$
C
$\left(4, \frac{27}{4}\right)$
D
$\left(4, \frac{23}{4}\right)$
Solution
$\begin{cases}f(x)=x^{3}-3 x, x \leq-1 \\ 2,-1 < x < 2 \\ x^{2}+2 x-6,2 < x < 3 \\ 9,3 \leq x < 4 \\ 10,4 \leq x < 5 \\ 11, x=5 \\ 2 x+1, x > 5\end{cases}$
Clearly $f ( x )$ is not differentiable at
$x =2,3,4,5 \Rightarrow m =4$
$I=\int\limits_{-2}^{-1}\left(x^{3}-3 x\right) d x+\int\limits_{-1}^{2} 2 \cdot d x=\frac{27}{4}$
A
3
B
4
C
5
D
6
Solution
$\frac{\overrightarrow{ a } \cdot \overrightarrow{ c }}{|\overrightarrow{ c }|}=\frac{10}{3}$
$\Rightarrow \frac{\alpha+6+2}{\sqrt{1+4+4}}=\frac{10}{3} \Rightarrow \alpha=2$
and $\left|\begin{array}{ccc}\hat{i} & \hat{ j } & \hat{ k } \\ 3 & -\beta & 4 \\ 1 & 2 & -2\end{array}\right|=-6 \hat{ i }+\hat{ j }+\hat{ k }$
$\Rightarrow 2 \beta-8=-6 \Rightarrow \beta=1$
$\Rightarrow \alpha+\beta=3$
A
$\frac{16 \sqrt{2}}{6}$
B
$\frac{11 \sqrt{2}}{6}$
C
$\frac{13 \sqrt{2}}{6}$
D
$\frac{5 \sqrt{2}}{6}$
Solution

Area of $\Delta ABC =\frac{1}{2}(\sqrt{2}) \cdot 1=\frac{\sqrt{2}}{2}$
So required Area $=\int\limits_{0}^{4}(\sqrt{8 x}-\sqrt{2} x) d x-\frac{\sqrt{2}}{2}$
$=\frac{32 \sqrt{2}}{3}-8 \sqrt{2}-\frac{\sqrt{2}}{2}=\frac{13 \sqrt{2}}{6}$
A
$-3$
B
3
C
6
D
9
Solution
$\begin{vmatrix} 2 & 1 & -1 \\ 1 & -3 & 2 \\ 1 & 4 & \delta\end{vmatrix}=0$
$\Rightarrow \delta=-3$
And $\begin{vmatrix} 7 & 1 & -1 \\1 & -3 & 2 \\K & 4 & -3\end{vmatrix}=0 $ $\Rightarrow K =6$
$\Rightarrow \delta+ K =3$
Alternate
$2 x+y-z=7....$(1)
$x-3 y+2 z=1.....$(2)
$x+4 y+\delta z=k .....$(3)
Equation (2) $+(3)$
We get $2 x + y +(2+\delta) z =1+ K ....$(4)
For infinitely solution
Form equation (1) and (4)
$2+\delta=-1 $
$\Rightarrow \delta=-3$
$1+ k =7 $
$\Rightarrow k =6 $
$\delta+ k =3$
A
50
B
250
C
1250
D
1500
Solution
$X ^{2}=1-2 i \Rightarrow \alpha^{2}=1-2 i , \beta^{2}=1-2 i$
Hence $\alpha^{8}=\beta^{8}$
$\left|\alpha^{8}+\beta^{8}\right|=\left|2\alpha^{8}\right|=2\left|\alpha^{2}\right|^{4} $
$=2 \sqrt{5}^{4}=50$
A
$\wedge$
B
$\vee$
C
$\Rightarrow$
D
$\Leftrightarrow$
Solution
$p \vee q \Rightarrow q$
$\Rightarrow \sim( p \vee q ) \vee q$
$\Rightarrow(\sim p \wedge \sim q ) \vee q$
$\Rightarrow(\sim p \vee q ) \wedge(\sim q \vee q )$
$\Rightarrow(\sim p \vee q ) \wedge t =\sim p \vee q$
Now by taking option $C$
$( p \wedge q ) \Rightarrow \sim p \vee q$
$\Rightarrow \sim p \vee \sim q \vee \sim p \vee q$
$\Rightarrow t$
A
$\left(\frac{3^{10}-3}{2}\right) A$
B
$\left(\frac{3^{10}-1}{2}\right) A$
C
$\left(\frac{3^{10}+1}{2}\right) A$
D
$\left(\frac{3^{10}+3}{2}\right) A$
Solution
$A =\begin{pmatrix} 1 & 2 & 2^{2} \\ 1 / 2 & 1 & 2 \\ 1 / 2^{2} & 1 / 2 & 1\end{pmatrix}$
$A ^{2}=3 A$
$A ^{3}=3^{2} A$
$A ^{2}+ A ^{3}+\ldots . A ^{10}$
$=3 A +3^{2} A +\ldots+3^{9} A =\frac{3\left(3^{9}-1\right)}{3-1} A$
$=\frac{3^{10}-3}{2} A$
A
reflexive, symmetric but not transitive
B
reflexive, transitive but not symmetric
C
reflexive but not symmetric and transitive
D
an equivalence relation
Solution
$A=\{1,2,3\}$
$R=\{(1,1),(1,2),(1,3)(2,1),(2,2),(2,3)(3,1)(3,2)(3,3)\}$
A
$\frac{6}{343}$
B
$\frac{7}{216}$
C
$\frac{8}{343}$
D
$\frac{49}{216}$
Solution
$a_{2}=1, a_{3}=3 a_{4}=6$
$a_{n}=\frac{n(n-1)}{2}$
$S=\displaystyle\sum_{n=2}^{\infty} \frac{n(n-1)}{2\left(7^{n}\right)}$
$S=\frac{1}{7^{2}}+\frac{3}{7^{3}}+\frac{6}{7^{4}}+\frac{10}{7^{5}}+\frac{15}{7^{5}}+\ldots \ldots$
$\frac{S}{7}=\frac{1}{7^{3}}+\frac{3}{7^{4}}+\frac{6}{7^{5}}+\frac{10}{7^{6}}+\ldots$
$6 \frac{S}{7}=\frac{1}{7^{2}}+\frac{2}{7^{3}}+\frac{3}{7^{4}}+\frac{4}{7^{5}}+\ldots$
$6 \frac{S}{7^{2}}=\frac{1}{7^{3}}+\frac{2}{7^{4}}+\frac{3}{7^{5}}+\ldots$
$6 \frac{S}{7} \cdot \frac{6}{7}=\frac{1}{7^{2}}+\frac{1}{7^{3}}+\ldots=\frac{1 / 7^{2}}{1-1 / 7}$
$6 \times 6 \frac{S}{7^{2}}=\cdot \frac{1}{7 \times 6}$
$S=\frac{7}{6^{3}}=\frac{7}{216}$
Alternate
$a_{n+2}=2 a_{n+1}-a_{n}+1$
$\Rightarrow \frac{a_{n+2}}{7^{n+2}}=\frac{2}{7} \frac{a_{n+1}}{7^{n+1}}-\frac{1}{49} \frac{a_{n}}{7^{n}}+\frac{1}{7^{n+2}} $
$\Rightarrow \displaystyle\sum_{n=2}^{\infty} \frac{a_{n+2}}{7^{n+2}}=\frac{2}{7} \displaystyle\sum_{n=2}^{\infty} \frac{a_{n+1}}{7^{n+1}}-\frac{1}{49} \displaystyle\sum_{n=2}^{\infty} \frac{a_{n}}{7^{n}}+\displaystyle\sum_{n=2}^{\infty} \frac{1}{7^{n+2}}$
Let $ \displaystyle\sum_{n=2}^{\infty} \frac{a_{n}}{7^{n}}=p $
$\Rightarrow\left(p-\frac{a_{2}}{7^{2}}-\frac{a_{3}}{7^{3}}\right)=\frac{2}{7}\left(p-\frac{a_{2}}{7^{2}}\right)-\frac{1}{49} p+\frac{1 / 7^{4}}{1-\frac{1}{7}}$
$\because a _{2}=1, a _{3}=3$
$\Rightarrow p -\frac{1}{49}-\frac{3}{343}=\frac{2}{7} p -\frac{2}{7^{3}}-\frac{ p }{49}+\frac{1}{6.7^{3}}$
$\Rightarrow p =\frac{7}{216}$
A
$10$
B
$\frac{48}{5}$
C
$\frac{52}{5}$
D
$3$
Solution

$M_{1}=3 / 2 \,\,\,\,M_{2}=2 / x$
$\tan \pi / 4=\left|\frac{3 / 2-2 / x}{1+6 / 2 x}\right|=1$
$\Rightarrow x_{1}=10, \,\,\,\,x_{2}=-2 / 5$
$\Rightarrow AA ^{1}=52 / 5$
A
$\frac{22}{9+4 \sqrt{3}}$
B
$\frac{66}{9+4 \sqrt{3}}$
C
$\frac{22}{4+9 \sqrt{3}}$
D
$\frac{66}{4+9 \sqrt{3}}$
Solution

$A _{ T }=\frac{\sqrt{3}}{4} a ^{2}+ b ^{2}$
$=\frac{\sqrt{3}}{4} x^{2} / 9+\frac{(22-x)^{2}}{16}$
$\frac{ dA }{ dx }=0 \Rightarrow x \left(\frac{\sqrt{3}}{2 \times 9}+\frac{1}{8}\right)-\frac{22}{8}=0$
$\Rightarrow x\left(\frac{4 \sqrt{3}+9}{36}\right)=\frac{11}{2}$
$a=x / 3$
$a=\left(\frac{11 / 2}{\frac{4 \sqrt{3}+9}{36}}\right)\left(\frac{1}{3}\right)=\frac{66}{4 \sqrt{3}+9}$
A
$R-\left\{-\frac{1}{2}, \frac{1}{2}\right\}$
B
$(-\infty,-1] \cup[1, \infty) \cup\{0\}$
C
$\left(-\infty, \frac{-1}{2}\right) \cup\left(\frac{1}{2}, \infty\right) \cup\{0\}$
D
$\left(-\infty, \frac{-1}{\sqrt{2}}\right] \cup\left[\frac{1}{\sqrt{2}}, \infty\right) \cup\{0\}$
Solution
$-1 \leq \frac{2 \sin ^{-1}\left(\frac{1}{4 x^{2}-1}\right)}{\pi} \leq 1$
$-\pi / 2 \leq \sin ^{-1} \frac{1}{4 x^{2}-1} \leq \pi / 2$
Always $-1 \leq \frac{1}{4 x^{2}-1} \leq 1$
$x \in\left(\infty, \frac{1}{\sqrt{2}}\right) \cup\left[\frac{1}{\sqrt{2}}, \infty\right)$
A
6
B
7
C
8
D
9
Solution
General term
$ T _{ r _{ r }}=\frac{\lfloor 10}{\lfloor r _{1}\lfloor r _{2} \lfloor r _{3}}(3)^{ r _{1}}(-2)^{ r _{2}}(5)^{ r _{3}}( x )^{3 r _{1}+2 r _{2}-5 r _{3}} $
$3 r _{1}+2 r _{2}-5 r _{3}=0 ....$(1)
$ r _{1}+ r _{2}+ r _{3}=10 \ldots $(2)
from equation (1) and (2)
$r _{1}+2\left(10- r _{3}\right)-5 r _{3}=0$
$ r _{1}+20=7 r _{3}$
$\left( r _{1}, r _{2}, r _{3}\right)=(1,6,3)$
constant term $=\frac{\lfloor 10}{\lfloor 1 \lfloor 6 \lfloor3}(3)^{1}(-2)^{6}(5)^{3}$
$=2^{9} \cdot 3^{2} \cdot 5^{4} \cdot 7^{1} $
$l=9$
A
-3
B
-2
C
2
D
0
Solution
$I=\int\limits_{0}^{5} \cos \left(\pi x-\pi\left[\frac{x}{2}\right]\right) d x$
$\Rightarrow I=\int\limits_{0}^{2} \cos (\pi x) d x+\int\limits_{2}^{4} \cos (\pi x-\pi) d x+\int\limits_{4}^{5} \cos (\pi x-2 \pi) d x$
$\Rightarrow I=\left[\frac{\sin \pi x}{\pi}\right]_{0}^{2}+\left[\frac{\sin (\pi x-\pi)}{\pi}\right]_{2}^{4}+\left[\frac{\sin (\pi x-2 \pi)}{\pi}\right]_{4}^{5}$
$\Rightarrow I=0$
A
$1+\sqrt{2}$
B
$3+2 \sqrt{2}$
C
$1+2 \sqrt{3}$
D
$4+5 \sqrt{3}$
Solution
$PQ$ is focal chord

$m _{ PR } \cdot m _{ PQ }=-1$
$\frac{2 t }{ t ^{2}-3} \times \frac{-2 / t }{\frac{1}{ t ^{2}}-3}=-1$
$\left( t ^{2}-1\right)^{2}=0$
$\Rightarrow t =1$
$\Rightarrow P \& Q$ must be end point of latus rectum:
$P (1,2) \& Q (1,-2)$
$\therefore \frac{2 b^{2}}{a}=4 \& a e=1$
$\because$ We know that $b ^{2}= a ^{2}\left(1- e ^{2}\right)$
$\therefore a =1+\sqrt{2}$
$\because e ^{2}=1-\frac{ b ^{2}}{ a ^{2}}$
$\therefore e ^{2}=3-2 \sqrt{2}$
$\frac{1}{ e ^{2}}=3+2 \sqrt{2}$
A
$\frac{1}{2}$
B
$\frac{2}{3}$
C
$\frac{1}{6}$
D
$\frac{5}{3}$
Solution
$OP =\left|\frac{2-3+2}{\sqrt{2}}\right|$
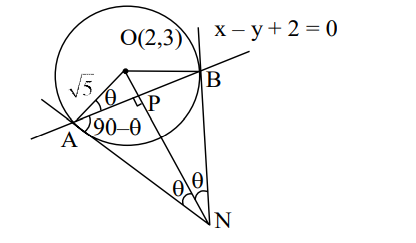
$OP =\frac{3}{\sqrt{2}} $
$ AP =\sqrt{ OA ^{2}- OP ^{2}}$
$=\frac{1}{\sqrt{2}} $
$\tan \theta=3 $
$\therefore \sin \theta=\frac{3}{\sqrt{10}}=\frac{ AP }{ AN } $
$\Rightarrow AN =\frac{\sqrt{5}}{3}= BN$
Area of $\triangle ANB =\frac{1}{2} \cdot\left( AN ^{2}\right) \sin 2 \theta=\frac{1}{6}$
A
13
B
15
C
17
D
18
Solution
$\overline{ x }=\frac{\displaystyle\sum x _{ i }}{5}=\frac{24}{5} $
$\Rightarrow \displaystyle\sum x _{ i }=24$
$\sigma^{2}=\frac{\displaystyle\sum x _{ i }^{2}}{5}-\left(\frac{24}{5}\right)^{2}=\frac{194}{25}$
$\Rightarrow \displaystyle\sum x _{ i }^{2}=154$
$x _{1}+ x _{2}+ x _{3}+ x _{4}=14$
$\Rightarrow x _{5}=10$
$\sigma^{2}=\frac{ x _{1}^{2}+ x _{2}^{2}+ x _{3}^{2}+ x _{4}^{2}}{4}-\frac{49}{4}= a$
$x _{1}^{2}+ x _{2}^{2}+ x _{3}^{2}+ x _{4}^{2}=4 a +49$
$x _{5}^{2}=154-4 a -49$
$\Rightarrow 100=105-4 a \Rightarrow 4 a =5$
$4 a + x _{5}=15$
Answer: 26
Solution
$| z -2| \leq 1$

$(x-2)^{2}+y^{2} \leq 1 \ldots \ldots(1)$
$\&$
$z(1+i)+\bar{Z}(1-i) \leq 2$
Put $z=x+i y$
$\therefore x - y \leq 1 \ldots(2)$
$ PA =\sqrt{17}, PB =\sqrt{13}$
Maximum is $PA $ & Minimum is $PD$
Let $D (2+\cos \theta, 0+\sin \theta)$
$\therefore m _{ cp }=\tan \theta=-2$
$\cos \theta=-\frac{1}{\sqrt{5}}, \sin \theta=\frac{2}{\sqrt{5}}$
$\therefore D \left(2-\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right)$
$\Rightarrow z _{1}=\left(2-\frac{1}{\sqrt{5}}\right)+\frac{2 i }{\sqrt{5}} $
$\left| z _{1}\right|=\frac{25-4 \sqrt{5}}{5} \& z _{2}=1$
$\therefore\left| z _{2}\right|^{2}=1$
$\therefore 5\left(\left| z _{1}\right|^{2}+\left| z _{2}\right|^{2}\right)=30-4 \sqrt{5} $
$\therefore \alpha=30$
$\beta=-4 $
$\therefore \alpha+\beta=26$
Answer: 2
Solution
$\frac{d y}{d x}+\frac{\sqrt{2}}{2 \cos ^{4} x-\cos 2 x} y=x e^{\tan ^{-1}(\sqrt{2} \cot 2 x)}$
$\int \frac{d x}{2 \cos ^{4} x-\cos 2 x}$
$=\int \frac{d x}{\cos ^{4} x+\sin ^{4} x}=\int \frac{\operatorname{cosec}^{4} x d x}{1+\cot ^{4} x}$
$=-\int \frac{t^{2}+1}{t^{4}+1} d t=-\int \frac{1}{\left(t-\frac{1}{t}\right)^{2}+2} d t$
$=\frac{-1}{\sqrt{2}} \tan ^{-1}\left(\frac{t-\frac{1}{t}}{\sqrt{2}}\right)$
$\operatorname{Cotx}=t$
$=-\frac{1}{\sqrt{2}} \tan ^{-1}(\sqrt{2} \cot 2 x)$
$\therefore IF =e^{-\tan ^{-1}(\sqrt{2} \cot 2 x )}$
$y e^{-\tan ^{-1}(\sqrt{2} \cot 2 x)}=\int x d x$
$y e^{-\tan ^{-1}(\sqrt{2} \cot 2 x)}=\frac{x^{2}}{2}+c$
$y\left(\frac{\pi}{4}\right)=\frac{\pi^{2}}{32}+c \Rightarrow c=0$
$y=\frac{x^{2}}{2} e^{\tan ^{-1}(\sqrt{2} \cot 2 x)}$
$y\left(\frac{\pi}{3}\right)=\frac{\pi^{2}}{18} e^{\tan ^{-1}\left(\sqrt{2} \cot \frac{2 \pi}{3}\right)}$
$=\frac{\pi^{2}}{18} e^{-\tan ^{-1}\left(\sqrt{\frac{2}{3}}\right)}$
$ \alpha=\frac{2}{3} \Rightarrow 3 \alpha^{2}=2$
Answer: 26
Solution
Points $P (1,2,-1)$ and $Q (2,-1,3)$ lie on same side of the plane.
Perpendicular distance of point $P$ from plane is
$\left|\frac{-1+2-1-1}{\sqrt{1^{2}+1^{2}+1^{2}}}\right|=\frac{1}{\sqrt{3}}$
Perpendicular distance of point $Q$ from plane is
$=\left|\frac{-2-1+3-1}{\sqrt{1^{2}+1^{2}+1^{2}}}\right|=\frac{1}{\sqrt{3}}$
$\Rightarrow \overrightarrow{ PQ }$ is parallel to given plane. So, distance between $P$ and $Q =$ distance between their foot of perpendiculars.
$\Rightarrow|\overrightarrow{ PQ }|=\sqrt{(1-2)^{2}+(2+1)^{2}+(-1-3)^{2}} $
$=\sqrt{26} $
$|\overrightarrow{ PQ }|^{2}=26= d ^{2}$
Alternate
$-x+y+z-1=0$

$\frac{x_{1}-1}{-1}=\frac{y_{1}-2}{1}=\frac{z_{1}+1}{1}=\frac{1}{3}$
$x _{1}=\frac{2}{3}, y_{1}=\frac{7}{3}, z_{1}=\frac{-2}{3}$
$M \left(\frac{2}{3}, \frac{7}{3}, \frac{-2}{3}\right)$
$N \left( x _{2}, y _{2}, z _{2}\right)$
$\frac{ x _{2}-2}{-1}=\frac{ y _{2}+1}{1}=\frac{ z _{2}-3}{1}=\frac{1}{3}$
$x _{2}=\frac{5}{3}, y _{2}=\frac{-2}{3}, z _{2}=\frac{10}{3}$
$N =\left(\frac{5}{3}, \frac{-2}{3}, \frac{10}{3}\right)$
$d ^{2}=1^{2}+3^{2}+4^{2}=26$
Answer: 32
Solution
$3 \cos ^{2} 2 \theta+6 \cos 2 \theta-10 \cos ^{2} \theta+5=0$
$3 \cos ^{2} 2 \theta+6 \cos 2 \theta-5(1+\cos 2 \theta)+5=0 $
$3 \cos ^{2} 2 \theta+\cos 2 \theta=0$
$\operatorname{Cos} 2 \theta=0 $ OR $\cos 2 \theta=-1 / 3 $
$\theta \in[-4 \pi, 4 \pi]$
$2 \theta=(2 n+1) \cdot \frac{\pi}{2} $
$\therefore \theta=\pm \pi / 4 . \pm 3 \pi / 4 \ldots \ldots \ldots \pm 15 \pi / 4$
Similarily $\cos 2 \theta=-1 / 3$ gives $16$ solution
Answer: 1
Solution
$2 \theta-\cos ^{2} \theta+\sqrt{2}=0$
$\Rightarrow \cos ^{2} \theta=2 \theta+\sqrt{2}$
$y=2 \theta+\sqrt{2}$

Both graphs intersect at one point.
Answer: 29
Solution
$50 \tan \left(3 \tan ^{-1} \frac{1}{2}+2 \cos ^{-1} \frac{1}{\sqrt{5}}\right)$
$+4 \sqrt{2} \tan \left(\frac{1}{2} \tan ^{-1} 2 \sqrt{2}\right)$
$=50 \tan \left(\tan ^{-1} \frac{1}{2}+2\left(\tan ^{-1} \frac{1}{2}+\tan ^{-1} 2\right)\right)$
$+4 \sqrt{2} \tan \left(\frac{1}{2} \tan ^{-1} 2 \sqrt{2}\right)$
$\left.=50 \tan \left(\tan ^{-1} \frac{1}{2}+2 \cdot \frac{\pi}{2}\right)\right)+4 \sqrt{2} \times \frac{1}{\sqrt{2}}$
$=50\left(\tan \tan ^{-1} \frac{1}{2}\right)+4$
$=25+4=29$
Answer: 3395
Solution
$
\begin{array}{l}
f(x)=(c+1) x^{2}+\left(1-c^{2}\right) x+2 k \\
\& f(x+y)=f(x)+f(y)-x y \forall x y \in R \\
\lim _{y \rightarrow 0} \frac{f(x+y)-f(x)}{y}=\lim _{y \rightarrow 0} \frac{f(y)-x y}{y} \\
f(x)=-\frac{1}{2} x^{2}+f^{\prime}(0) \cdot x+\lambda \text { but } f(0)=0 \\
\therefore(x)=-\frac{1}{2} x^{2}+\left(1-c^{2}\right) \cdot x \\
\therefore \text { as } f^{\prime}(0)=1-c^{2}
\end{array}
$
Comparing equation (1) and (2)
We obtain, $c=-3 / 2$
$
\therefore f ( x )=-\frac{1}{2} x ^{2}-\frac{5}{4} x
$
Now $\left|2 \sum_{x=1}^{20} f(x)\right|=\sum_{x=1}^{20} x^{2}+\frac{5}{2} \cdot \sum_{x=1}^{20} x$
$
=2870+525
$
$
=3395
$
Answer: 88
Solution
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
Given $e^{2}=1+\frac{b^{2}}{a^{2}} \Rightarrow \frac{11}{4}=1+\frac{b^{2}}{a^{2}} \Rightarrow b^{2}=\frac{7}{4} a^{2}$
$\therefore \frac{x^{2}}{(a)^{2}}-\frac{y^{2}}{\left(\frac{\sqrt{7}}{2} a\right)^{2}}=1$ Now given
$2 a +2 \cdot \frac{\sqrt{7} a }{2}=4(2 \sqrt{2}+\sqrt{14}) $
$ a (2+\sqrt{7})=4 \sqrt{2}(2+\sqrt{7}) $
$ a =4 \sqrt{2} \Rightarrow a ^{2}=32 $
$b ^{2}=\frac{7}{4} \times 16 \times 2=56$
Answer: 28
Solution
$P_{1}: \vec{r} \cdot(2 \hat{i}+\hat{j}-3 \hat{k})=4$
$P_{1}: 2 x+y-3 z=4$
$P_{2} \begin{vmatrix}x-2 & y+3 & z-2 \\0 & 1 & -5 \\-1 & -1 & 0\end{vmatrix}=0 $
$\Rightarrow-5 x+5 y+z+23=0$
Let a, b, c be the d'rs of line of intersection
Then $ a =\frac{16 \lambda}{15} ; b =\frac{13 \lambda}{15} ; c =\frac{15 \lambda}{15} $
$\therefore \alpha=13: \beta=15$
Answer: 18915