JEE Main Question Paper with Solution 2022 July 29th Shift 1 - Morning

JEE Main Physics Question Paper with Solution 2022 July 29th Shift 1 - Morning

Q1. Given below are two statements: One is labelled as Assertion (A) and other is labelled as Reason (R).
Assertion (A) : Time period of oscillation of a liquid drop depends on surface tension (S), if density of the liquid is $p$ and radius of the drop is $r$, then $T = k \sqrt{ pr ^3 / s ^{3 / 2}}$ is dimensionally correct, where $K$ is dimensionless.
Reason (R) : Using dimensional analysis we get R.H.S. having different dimension than that of time period.
In the light of above statements, choose the correct answer from the options given below.

A

Both (A) and (R) are true and (R) is the correct explanation of (A)

B

Both (A) and (R) are true but (R) is not the correct explanation of (A)

C

(A) is true but $( R )$ is false

D

(A) is false but (R) is true

Solution

$T = k \sqrt{\frac{\rho r^3}{ s ^{3 / 2}}}$
Dimensions of RHS
$\frac{\left[ M ^{1 / 2} L ^{-3 / 2}\right]\left[ L ^{3 / 2}\right]}{\left[ MT ^{-2}\right]^{3 / 4}}= M ^{1 / 8} L ^0 T ^{3 / 2}$
Dimensions of L.H.S $\neq$ Dimensions of R.H.S

Q2. A ball is thrown up vertically with a certain velocity so that, it reaches a maximum height h. Find the ratio of the times in which it is at height $\frac{ h }{3}$ while going up and coming down respectively.

A

$\frac{\sqrt{2}-1}{\sqrt{2}+1}$

B

$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$

C

$\frac{\sqrt{3}-1}{\sqrt{3}+1}$

D

$\frac{1}{3}$

Solution

image
$ \text { Max. Height }= h =\frac{ u ^2}{2 g } $
$ \Rightarrow u =\sqrt{2 gh }$
$ S = ut +\frac{1}{2} at ^2$
$ \frac{ h }{3}=\sqrt{2 ght }+\frac{1}{2}(- g ) t ^2$
$ \frac{ gt ^2}{2}-\sqrt{2 ght }+\frac{ h }{3}=0$
(Roots are $t _1 \& t _2$ )
$\frac{ t _2}{ t _1}=\frac{\sqrt{2 gh }+\sqrt{2 gh -4 \times \frac{ g }{2} \times \frac{ h }{3}}}{\sqrt{2 gh }-\sqrt{2 gh -4 \times \frac{ g }{2} \times \frac{ h }{3}}}$
$=\frac{\sqrt{2 gh }+\sqrt{\frac{4 gh }{3}}}{\sqrt{2 gh }-\sqrt{\frac{4 gh }{3}}}=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$

Q3. If $t=\sqrt{x}+4$, then $\left(\frac{d x}{d t}\right)_{t=4}$ is:

A

4

B

Zero

C

8

D

16

Solution

$ t =\sqrt{ x }+4 $
$ \Rightarrow x =( t -4)^2= t ^2-8 t +16 $
$ \Rightarrow \frac{ dx }{ dt }=2 t -8 $
$ \left.\Rightarrow \frac{ dx }{ dt }\right|_{ t =4}=2 \times 4-8=0$

Q4. A smooth circular groove has a smooth vertical wall as shown in figure. A block of mass $m$ moves against the wall with a speed v. Which of the following curve represents the correct relation between the normal reaction on the block by the wall $( N )$ and speed of the block (v) ?

A

B

C

D

Solution

$N =\frac{ mv ^2}{ r }$
Curve is parabola
$Y = kx ^2$

Q5. A ball is projected with kinetic energy E, at an angle of $60^{\circ}$ to the horizontal. The kinetic energy of this ball at the highest point of its flight will become :

A

Zero

B

$\frac{E}{2}$

C

$\frac{E}{4}$

D

$E$

Solution

image
$E =\frac{1}{2} mu ^2$
At Highest point, Velocity $V = u \cos 60^{\circ}=\frac{ u }{2}$
$\therefore K . E$ at topmost point $=\frac{1}{2} m \left(\frac{ u }{2}\right)^2=\frac{ E }{4}$

Q6. Two bodies of mass $1 kg$ and $3 kg$ have position vectors $\hat{ i }+2 \hat{ j }+\hat{ k }$ and $-3 \hat{ i }-2 \hat{ j }+\hat{ k }$ respectively. The magnitude of position vector of centre of mass of this system will be similar to the magnitude of vector :

A

$\hat{i}-2 \hat{j}+\hat{k}$

B

$-3 \hat{i}-2 \hat{j}+\hat{k}$

C

$-2 \hat{i}+2 \hat{k}$

D

$-2 \hat{i}-\hat{j}+2 \hat{k}$

Solution

$\overrightarrow{r_{c o m}}= \frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}}{m_1+m_2}=\frac{1(\hat{ i }+2 \hat{ j }+\hat{ k })+3(-3 \hat{ i }-2 \hat{ j }+\hat{ k })}{1+3} $
$= -2 \hat{ i }-\hat{ j }+\hat{ k }$
$ |2 \hat{ i }-\hat{ j }+\hat{ k }|=\sqrt{(2)^2+(1)^2+(1)^2}=\sqrt{6}$

Q7. Given below are two statements : One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Clothes containing oil or grease stains cannot be cleaned by water wash.
Reason (R) : Because the angle of contact between the oil/ grease and water is obtuse. In the light of the above statements, choose the correct answer from the option given below.

A

Both (A) and (R) are true and (R) is the correct explanation of (A)

B

Both (A) and (R) are true but (R) is not the correct explanation of (A)

C

(A) is true but (R) is false

D

(A) is true but (R) is true

Q8. If the length of a wire is made double and radius is halved of its respective values. Then, the Young's modules of the material of the wire will :

A

Remains same

B

Become 8 times its initial value

C

Become $\frac{1^{\text {th }}}{4}$ of its initial value

D

Become 4 times its initial value

Solution

Y depends on material of wire

Q9. The time period of oscillation of a simple pendulum of length $L$ suspended from the roof of a vehicle, which moves without friction down an inclined plane of inclination $\alpha$, is given by :

A

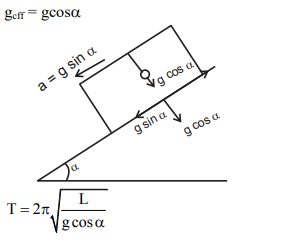
$2 \pi \sqrt{ L /( g \cos \alpha)}$

B

$2 \pi \sqrt{ L /( g \sin \alpha)}$

C

$2 \pi \sqrt{ L / g }$

D

$2 \pi \sqrt{ L /( g \tan \alpha)}$

Solution

image

Q10. A spherically symmetric charge distribution is considered with charge density varying as $\rho(r)= \begin{cases}\rho_0\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{cases}$ Where, $r ( r < R )$ is the distance from the centre $O$ (as shown in figure). The electric field at point $P$ will be :

A

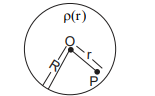
$\frac{\rho_0 r}{4 \varepsilon_0}\left(\frac{3}{4}-\frac{r}{R}\right)$

B

$\frac{\rho_0 r}{3 \varepsilon_0}\left(\frac{3}{4}-\frac{r}{R}\right)$

C

$\frac{\rho_0 r}{4 \varepsilon_0}\left(1-\frac{r}{R}\right)$

D

$\frac{\rho_0 r }{5 \varepsilon_0}\left(1-\frac{ r }{ R }\right)$

Solution

image
$ \oint \overrightarrow{ E } \cdot d \overrightarrow{ s }=\frac{Q_{ in }}{\varepsilon_{ o }} $
$ E \cdot 4 \pi r ^2=\frac{\int\limits_0^{ r } \rho_{ o }\left(\frac{3}{4}-\frac{ r }{ R }\right) 4 \pi r ^2 dr }{\varepsilon_0} $
$ E 4 \pi r ^2=\frac{\rho_{ o } 4 \pi}{\varepsilon_{ o }}\left(\frac{3}{4} \frac{ r ^3}{3}-\frac{ r ^4}{4 R }\right) $
$ Er r ^2=\frac{\rho_{ o } r ^3}{4 \varepsilon_o}\left\{1-\frac{ r }{ R }\right\} $
$ E =\frac{\rho_{ o } r }{4 \varepsilon_{ o }}\left\{1-\frac{ r }{ R }\right\}$

Q11. Given below are two statements.
Statement I : Electric potential is constant within and at the surface of each conductor.
Statement II : Electric field just outside a charged conductor is perpendicular to the surface of the conductor at every point.
In the light of the above statements, choose the most appropriate answer from the options give below.

A

Both statement I and statement II are correct

B

Both statement I and statement II are incorrect

C

Statement I is correct but statement II is incorrect

D

Statement $I$ is incorrect but and statement II is correct

Solution

(Properties of conductor)
Statement - I, true as body of conductor acts as equipotential surface.
Statement - 2 True, as conductor is equipotential. Tangential component of electric field should be zero. Therefore electric field should be perpendicular to surface

Q12. Two metallic wires of identical dimensions are connected is series. If $\sigma_1$ and $\sigma_2$ are the conductivities of the these wires respectively, the effective conductivity of the combination is :

A

$\frac{\sigma_1 \sigma_2}{\sigma_1+\sigma_2}$

B

$\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}$

C

$\frac{\sigma_1+\sigma_2}{2 \sigma_1 \sigma_2}$

D

$\frac{\sigma_1+\sigma_2}{\sigma_1 \sigma_2}$

Solution

image
Let length of wire be ' $\ell$ '
Area of wire as ' $A$ '
For equivalent wire length $=2 \ell \&$ area will be A
Thermal resistance
$ R _{ eq }= R _1+ R _2$
$\frac{2 \ell}{\sigma_{ eq } A }=\frac{\ell}{\sigma_1 A }+\frac{\ell}{\sigma_1 A }$
$ \frac{2 \ell}{\sigma_{ eq }}=\frac{\ell}{\sigma_1}+\frac{\ell}{\sigma_2} $
$\Rightarrow \sigma_{ eq }=\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}$

Q13. An alternating emf $E =440 \sin 100 \pi t$ is applited to a circuit containing an inductance of $\frac{\sqrt{2}}{\pi} H$. If an a.c. ammeter is connected in the circuit, its reading will be :

A

$4.4 A$

B

$1.55 A$

C

$2.2 A$

D

$3.11 A$

Solution

$ E =440 \operatorname{Sin} 100 \pi t, L=-\frac{\sqrt{2}}{\pi} H $
$ X _{ L }=\omega L =100 \pi \frac{\sqrt{2}}{\pi}=100 \sqrt{2} \Omega$
$ \text { Peak current } I _0=\frac{ E _0}{ X _{ L }}=\frac{440}{100 \sqrt{2}}=2.2 \sqrt{2} A$
$AC$ ammeter reads RMS value therefore reading will be $I _{ rms }$
$I _{ rms }=\frac{ I _0}{\sqrt{2}}=2.2 A$

Q14. A coil of inductance $1 H$ and resistance $100 \Omega$ is connected to a battery of $6 V$. Determine approximately :
(a) The time elapsed before the current acquires half of its steady - state value
(b) The energy stored in the magnetic field associated with the coil at an instant $15 ms$ after the circuit is switched on.
(Given $\operatorname{In} 2=0.693, e ^{-3 / 2}=0.25$ )

A

t = 10 ms; U = 2 mJ

B

t = 10 ms; U = 1 mJ

C

t = 7 ms; U = 1 mJ

D

t = 7 ms; U = 2 mJ

Solution

Given circuit is R - L growth circuit
image
$ i=\frac{E}{R}\left(1-e^{-t / \tau}\right) $
$ i=\frac{E}{2 R}=\frac{E}{R}\left(1-e^{-t / \tau)}\right)$
Solving $t =\tau \ln 2$
$ t =\frac{1}{R} \ln 2=\frac{1}{100} 0.693=0.00693$
$ =7 ms$
$ i(15 ms )=\frac{E}{R}\left(1- e ^{-\frac{15}{10}}\right)$
$ i =\frac{6}{100}(1-1 / 4)=\frac{3}{4} \times \frac{6}{100} $
$U=\frac{1}{2} LI ^2$
by solving we get $U =1\, mJ$.

Q15. Match List - I with List - II
List - I List - II
a UV rays i Diagnostic tool in medicine
b X-rays ii Water purification
c Microwave iii Communication,Radar
d Infrared wave iv Improving visibilityin foggy days
Choose the correct answer from the options given below :

A

(a)-(iii), (b)-(ii), (c)-(i), (d)-(iv)

B

(a)-(ii), (b)-(i), (c)-(iii), (d)-(iv)

C

(a)-(ii), (b)-(iv), (c)-(iii), (d)-(i)

D

(a)-(iii), (b)-(i), (c)-(ii), (d)-(iv)

Solution

(a) uv rays - used for water purification
(b) x-rays used for diagnosing fracture
(c) Microwaves are used for mobile and radar communication
(d) Infrared waves show less scattering therefore used in foggy days
(a - ii), (b - i), (c - iii), (d - iv)

Q16. The kinetic energy of emitted electron is $E$ when the light incident on the metal has wavelength $\lambda$. To double the kinetic energy, the incident light must have wavelength :

A

$\frac{h c}{E \lambda-h c}$

B

$\frac{h c \lambda}{E \lambda+h c}$

C

$\frac{ h \lambda}{ E \lambda+ hc }$

D

$\frac{h c \lambda}{E \lambda-h c}$

Solution

$ E =\frac{ hc }{\lambda}-\phi-( i ) $
$ 2 E =\frac{ hc }{\lambda^{\prime}}-\phi-(\text { ii) }$
(ii) - (i)
$E = hc \left(\frac{1}{\lambda^{\prime}}-\frac{1}{\lambda}\right) $
$ \Rightarrow \lambda^{\prime}=\frac{ hc \lambda}{ E \lambda+ hc }$

Q17. Find the ratio of energies of photons produced due to transition of an election of hydrogen atom from its(i) second permitted energy level to the first level, and (ii) the highest permitted energy level to the first permitted level.

A

$3: 4$

B

$4: 3$

C

$1: 4$

D

$4: 1$

Solution

$E _{ n }=\frac{-13.6}{ n ^2} ev $
$ \Rightarrow \frac{ E _2- E _1}{ E _{\infty}- E _1}=\frac{13.6\left(1-\frac{1}{4}\right)}{13.6}=\frac{3}{4}$

Q18. Find the modulation index of an AM wave having $8 V$ variation where maximum amplitude of the AM wave is $9 V$.

A

$0.8$

B

$0.5$

C

$0.2$

D

$0.1$

Solution

Modulation index: $m=\frac{A_m}{A_c}$
Given $2 A_m=8$
$ A _{ m }+ A _{ c }=9 \Rightarrow A _{ c }=5$
$ \therefore m =\frac{4}{5}=0.8$

Q19. A travelling microscope has $20$ divisions per $cm$ on the main scale while its Vernier scale has total $50 $ divisions and $25$ Vernier scale divisions are equal to $24$ main scale divisions, what is the least count of the travelling microscope ?

A

0.001 cm

B

0.002 mm

C

0.002 cm

D

0.005 cm

Solution

$ 1 MSD =\frac{1}{20} cm $
$1 VSD =\frac{24}{25} MSD =\frac{24}{25} \times \frac{1}{20} cm$
$ \therefore \text { Least count }=\frac{1}{20}\left(1-\frac{24}{25}\right) cm $
$=\frac{1}{20} \times \frac{1}{25}=\frac{1}{500} cm $
$ =0.002\, cm$

Q20. In an experiment to find out the diameter of wire using screw gauge, the following observation were noted :
image
(a) Screw moves $0.5 \,mm$ on main scale in one complete rotation
(b) Total divisions on circular scale $=50$
(c) Main scale reading is $2.5 \,mm$
(d) $45^{\text {th }}$ division of circular scale is in the pitch line
(e) Instrument has $0.03 \, mm$ negative error
Then the diameter of wire is :

A

$2.92 \, mm$

B

$2.54 \,mm$

C

$2.98 \, mm$

D

$3.45 \,mm$

Solution

$ \text{MSR}=2.5 mm $
$ \text{CSR}=45 \times \frac{0.5}{50} mm $
$ =0.45 \,mm$
Diameter reading $=$ MSR $+$ CSR $-$ zero error
$ =2.5+0.45-(-0.03)$
$ =2.98 \,mm$

Q21. An object is projected in the air with initial velocity $u$ at an angle $\theta$. The projectile motion is such that the horizontal range $R$, is maximum. Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ___degree.

Answer: 75

Solution

$ R _{\max }=\frac{ u ^2 \sin 2\left(45^{\circ}\right)}{ g }=\frac{ u ^2}{ g }$
$ \frac{ R }{2}=\frac{ u ^2}{2 g }=\frac{ u ^2 \sin 2 \theta}{ g }$
$\sin 2 \theta=\frac{1}{2}$
$ 2 \theta=30^{\circ}, 150^{\circ}$
$ \theta=15^{\circ}, 75^{\circ}$

Q22. If the acceleration due to gravity experienced by a point mass at a height $h$ above the surface of earth is same as that of the acceleration due to gravity at a depth $\alpha h$ (h $\ll R_e$ ) from the earth surface. The value of $\alpha$ will be
(use $R_e=6400 \,km$ )

Answer: 2

Solution

$ g \left(1-\frac{2 h }{ R }\right)= g \left(1-\frac{ d }{ R }\right) $
$ \frac{2 h }{ R }=\frac{ d }{ R }$
$ \alpha h = d$
$ \alpha=2$

Q23. The pressure $P_1$ and density $d_1$ of diatomic gas $\left(\gamma=\frac{7}{5}\right)$ changes suddenly to $P _2\left(> P _1\right)$ and $d _2$ respectively during an adiabatic process. The temperature of the gas increases and becomes ___ times of its initial temperature.
(given $\frac{ d _2}{ d _1}=32$ )

Answer: 4

Solution

$ PV ^\gamma=\text { const } \quad d =\frac{ m }{ V } $
$ p \left(\frac{ m }{ d }\right)^\gamma=\text { const } $
$ \frac{ p }{ d ^\gamma}=\text { const } $
$ \frac{ p _1}{ p _2}=\left(\frac{ d _1}{ d _2}\right)^\gamma=\left(\frac{1}{32}\right)^{7 / 5}=\frac{1}{128} $
$ \frac{ T _1}{ T _1}=\frac{ P _1 V _1}{ P _2 V _2}=\frac{1}{128} 32=\frac{1}{4}$

Q24. One mole of a monoatomic gas is mixed with three moles of a diatomic gas. The molecular specific heat of mixture at constant volume is $\frac{\alpha^2}{4} R J / mol K$; then the value of $\alpha$ will be ____. (Assume that the given diatomic gas

Answer: 3

Solution

$ C _{ v } / mix =\frac{ n _1 Cv _1+ n _2 Cv _2}{ n _1+ n _2}$
$ =\frac{1 \cdot \frac{3 R }{2}+3 \cdot \frac{5 R }{2}}{1+3} $
$ =\frac{9 R }{4}=\frac{\alpha^2}{4} R$
$ \alpha=3$

Q25. The current I flowing through the given circuit will be __________ $A$

Answer: 2

Q26. A closely wounded circular coil of radius $5 \,cm$ produces a magnetic field of $37.68 \times 10^{-4} T$ at its center. The current through the coil is ____$A$.
[Given, number of turns in the coil is $100$ and $\pi=3.14]$

Answer: 3

Solution

$ B_{\text {centre }}=\frac{N \mu_0 1}{2 R} $
$ 37.68 \times 10^{-4}=\frac{100 \times 4 \pi \times 10^{-7} \times I }{2 \times 5 \times 10^{-2}} $
$ I =3 A $

Q27. Two light beams of intensities $4 I$ and 9I interfere on a screen. The phase difference between these beams on the screen at point $A$ is zero and at point $B$ is $\pi$. The difference of resultant intensities, at the point A and B, will be___ $I$

Answer: 24

Solution

$ I _{ net }= I _1+ I _2+2 \sqrt{ I _1} \sqrt{ I _2} \cos \phi $
$ I _{\max } \text { for } \phi=0 \& I _{\min } \text { for } \phi=\pi $
$ I _{\max }=\left(\sqrt{ I _1}+\sqrt{ I _2}\right)^2=(\sqrt{9 I }+\sqrt{4 I })^2=25 I $
$ I _{\min }=\left(\sqrt{ I _1}-\sqrt{ I _2}\right)^2=(\sqrt{9 I }-\sqrt{4 I })^2= I $
$ I _{\max }- I _{\min }=25 I - I =24 I $

Q28. A wire of length $314 \,cm$ carrying current of $14 A$ is bent to form a circle. The magnetic moment of the coil is ____A- $m ^2$. [Given $\pi=3.14]$

Answer: 11

Solution

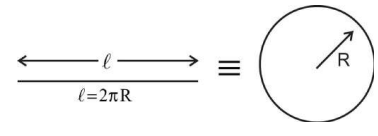
image
$ \frac{314}{100}=2 \pi R R =0.5 \,m$
Magnetic Moment $= IA $
$=14 \times \pi R ^2 $
$=14 \times(3.14) \times \frac{1}{4} $
$=10.99 \approx 11.00$

Q29. The $X - Y$ plane be taken as the boundary between two transparent media $M _1$ and $M _2$. $M_1$ in $Z \geq 0$ has a refractive index of $\sqrt{2}$ and $M _2$ with $Z <0$ has a refractive index of $\sqrt{3}$. A ray of light travelling in $M _1$ along the direction given by the vector $\vec{A}=4 \sqrt{3} \hat{i}-3 \sqrt{3} \hat{j}-5 \hat{k}$, is incident on the plane of separation. The value of difference between the angle of incident in $M _1$ and the angle of refraction in $M _2$ will be ____ degree.

Answer: 15

Solution

image
As incident vector A makes $i$ angle with normal z-axis \& refracted vector $R$ makes $r$ angle with normal $z$ - axis with help of direction cosine
$ i = \cos ^{-1}\left(\frac{ A _z}{ A }\right)=\cos ^{-1}\left(\frac{5}{\sqrt{(4 \sqrt{3})^2+(3 \sqrt{3})^2+5^2}}\right) $
$= \cos ^{-1}\left(\frac{5}{10}\right) \Rightarrow i =60^{\circ}$
$ \sqrt{2} \sin 60=\sqrt{3} \times \sin r $
$ r =45^{\circ}$
Difference between$ i \,\&\, r =60-45=15$

Q30. If the potential barrier across a p-n junction is $0.6 V$. Then the electric field intensity, in the depletion region having the width of $6 \times 10^{-6} m$, will be ____ $\times 10^5 N / C$.

Answer: 1

Solution

image
$ E =\frac{ V }{ d }=\frac{\text { Potential barrier Across Junction }}{\text { width of Depletion layer }} $
$ =\frac{0.6 V }{6 \times 10^{-6} m }=1 \times 10^5 V / m$
$ =1 \times 10^5\, N / C$

JEE Main Chemistry Question Paper with Solution 2022 July 29th Shift 1 - Morning

Q1. Which of the following pair of molecules contain odd electron molecule and an expanded octet molecule?

A

$BCl _3$ and $SF _6$

B

$NO$ and $H _2 SO _4$

C

$SF _6$ and $H _2 SO _4$

D

$BCl _3$ and $NO$

Solution

(A)$BCl _3 \rightarrow$ Even Electron molecule
$SF _6 \rightarrow$ Expanded octet molecule
(B) $NO \rightarrow$ Odd Electron molecule
$H _2 SO _4 \rightarrow$ Expanded octet.
(C) $SF _6 \rightarrow$ Even Electron molecule
$H _2 SO _4 \rightarrow$ Expanded octet.
(D) $BCl _3 \rightarrow$ Even Electron molecule
$NO \rightarrow$ Odd Electron molecule

Q2. $\underset{20\, g}{N _{2( g )}}+\underset{5 \,g}{3 H _{2( g )}} \rightleftharpoons 2 NH _{3( g )}$ Consider the above reaction, the limiting reagent of the reaction and number of moles of $NH _3$ formed respectively are:

A

$H _2, 1.42$ moles

B

$H _2, 0.71$ moles

C

$N _2, 1.42$ moles

D

$N _2, 0.71$ moles

Solution

$ \underset{W _2=20\, g}{N _2( g )}+\underset{5\, g}{3 H _2( g )} \rightleftharpoons 2 NH _3( g )$
$ n =\frac{20}{28} \frac{5}{2}$
Stoichiometric Amount:
$N _2 \rightarrow \frac{20 / 28}{1}=\frac{20}{28} H _2 \rightarrow \frac{5 / 2}{3}=\frac{5}{6}$
$\therefore N _2$ is the Limiting Reagent.
$\therefore n \left( NH _3\right) =2 \times n \left( N _2\right)=2 \times \frac{20}{28} $
$=1.42$

Q3. $100\, mL$ of $5 \%( w / v )$ solution of $NaCl$ in water was prepared in $250 \,mL$ beaker. Albumin from the egg was poured into $NaCl$ solution and stirred well. This resulted in a/ an :

A

Lyophilic sol

B

Lyophobic sol

C

Emulsion

D

Precipitate

Solution

Standard method for the preparation of lyophilic sol. (Discussed in lab Manual)

Q4. The first ionization enthalpy of $Na , Mg$ and Si, respectively, are: $496, 737 $ and $786 \,kJ \,mol ^{-1}$. The first ionization enthalpy $\left( kJ \,mol ^{-1}\right)$ of $Al$ is:

A

487

B

768

C

577

D

856

Solution

I. E : $Na < Al < Mg < Si$
$\therefore 496< IE ( Al )<737$
Option (C), matches the condition.
i.e $\text{IE}( Al )=577\, kJ\,mol ^{-1}$

Q5. In metallurgy the term "gangue" is used for:

A

Contamination of undesired earthy materials.

B

Contamination of metals, other than desired metal

C

Minerals which are naturally occuring in pure form

D

Magnetic impurities in an ore.

Solution

Earthy and undesired materials present in the ore, other then the desired metal, is known as gangue.

Q6. The reaction of zinc with excess of aqueous alkali, evolves hydrogen gas and gives :

A

$Zn ( OH )_2$

B

$ZnO$

C

$\left[ Zn ( OH )_4\right]^{2-}$

D

$\left[ ZnO _2\right]^{2-}$

Solution

Zinc dissolves in excess of aqueous alkali
$Zn +2 OH ^{-}+2 H _2 O \rightarrow \underset{\text{Tetrahydroxozincate(II) ion}}{\left[ Zn ( OH )_4\right]^{2-}+ H _2 \uparrow}$
However, this reaction in NCERT is given as
$Zn +2 NaOH \rightarrow Na _2 ZnO _2+ H _2 \uparrow$
$ZnO _2^{2-}$ is anhydrous form of $\left[ Zn ( OH )_4\right]^{2-}$
So in aqueous medium best answer of this question is $\left[ Zn ( OH )_4\right]^{2-}$

Q7. Lithium nitrate and sodium nitrate, when heated separately, respectively, give :

A

$LiNO _2$ and $NaNO _2$

B

$Li _2 O$ and $Na _2 O$

C

$Li _2 O$ and $NaNO _2$

D

$LiNO _2$ and $Na _2 O$

Solution

$Li _2 O , NaNO _2$
As per NCERT Lithium nitrate when heated gives lithium oxide, $Li _2 O$, whereas other alkali metal nitrates decompose to give the corresponding nitrite.
$4 LiNO _3 \longrightarrow 2 Li _2 O +4 NO _2+ O _2$
$2 NaNO _3 \longrightarrow 2 NaNO _2+ O _2$
However, the decomposition product of $NaNO _3$ are temperature dependent process as shown in the below reaction.

Q8. Number of lone pairs of electrons in the central atom of $SCl _2, O _3, ClF _3$ and $SF _6$, respectively, are :

A

$0,1,2$ and 2

B

$2,1,2$ and 0

C

$1,2,2$ and 0

D

$2,1,2$ and 0.

Q9. In following pairs, the one in which both transition metal ions are colourless is :

A

$Sc ^{3+}, Zn ^{2+}$

B

$Ti ^{4+}, Cu ^{2+}$

C

$V ^{2+}, Ti ^{3+}$

D

$Zn ^{2+}, Mn ^{2+}$

Solution

image
No $d - d$ transitions in ions with $d ^{\circ} \,\&\, d ^{10}$ configuration. Therefore they are colourless.

Q10. In neutral or faintly alkaline medium, $KMnO _4$ being a powerful oxidant can oxidize, thiosulphate almost quantitatively, to sulphate. In this reaction overall change in oxidation state of manganese will be :

A

5

B

1

C

0

D

3

Solution

$8 \overset{+7}{M}nO _4^-+3 S _2 O _3{ }^{2-}+ H _2 O \rightarrow 8 \overset{+4}{M}nO _2+6 SO _4{ }^{2-}+2 OH ^{-}$
Change in oxidation state of $Mn$ is from $+7$ to $+4$ which is 3 .

Q11. Which among the following pairs has only herbicides ?

A

Aldrin and Dieldrin

B

Sodium chlorate and Aldrin

C

Sodium arsinate and Dieldrin

D

Sodium chlorate and sodium arsinite.

Solution

Both sodium chlorate and sodium arsenite behave as herbicide.

Q12. Which among the following is the strongest Bronsted base ?

A

B

C

D

Q13. Which among the following pairs of the structures will give different products on ozonolysis? (Consider the double bonds in the structures are rigid and not delocalized.)

A

B

C

D

Q14. image
Considering the above reactions, the compound '$A$' and compound '$B$' respectively are :

A

B

C

D

Q15. image
Consider the above reaction sequence, the Product ‘$C$’ is :

A

B

C

D

Q16. image
Consider the above reaction, the compound ‘$A$’ is :

A

B

C

D

Q17. image
Which among the following represent reagent $A$?

A

B

C

D

Q18. Consider the following reaction sequence :

A

B

C

D

Q19. Which of the following compounds is an example of hypnotic drug ?

A

Seldane

B

Amytal

C

Aspartame

D

Prontosil

Solution

Amytal is hypnotic drug used to treat sleeping disorder.

Q20. A compound ' $X$ ' is acidic and it is soluble in $NaOH$ solution, but insoluble in $NaHCO _3$ solution. Compound ' $X$ ' also gives violet colour with neutral $FeCl _3$ solution. The compound ' $X$ ' is :

A

B

C

D

Q21. Resistance of a conductivity cell (cell constant $129\, m ^{-1}$ ) filled with $74.5 \, ppm$ solution of $KCl$ is $100 \, \Omega$ (labelled as solution 1). When the same cell is filled with $KCl$ solution of $149 \, ppm$, the resistance is $50 \Omega$ (labelled as solution 2). The ratio of molar conductivity of solution 1 and solution 2 is i.e. $\frac{\wedge_1}{\wedge_2}=x \times 10^{-3}$. The value of $x$ is___ (Nearest integer)
Given, molar mass of $KCl$ is $74.5\, g \, mol ^{-1}$

Answer: 1000

Solution

$\frac{\ell}{ A }=129\, m ^{-1}$
KCl solution 1 :
$74.5\, ppm , R _1=100\, \Omega$
$KCl$ solution 2 :
$149 \,ppm , R _2=50 \,\Omega$
$149 \,ppm , R _2=50 \, \Omega$
Here, $\frac{ ppm _1}{ ppm _2}=\frac{ M _1}{ M _2}\left(=\frac{ W _1 / M _0}{ V } \times \frac{ V }{ W _2 / M _0}\right)$
$\frac{\wedge_1}{\wedge_2}=\frac{\kappa_1 \times \frac{1000}{M_1}}{\kappa_2 \times \frac{1000}{M_2}}$
$ =\frac{\kappa_1}{\kappa_2} \times \frac{M_2}{M_1}$
$ =\frac{50}{100} \times 2 $
$ =\frac{\wedge_1}{\wedge_2}=1,000 \times 10^{-3}$

Q22. Ionic radii of cation $A ^{+}$and anion $B ^{-}$are 102 and $181 pm$ respectively. These ions are allowed to crystallize into an ionic solid. This crystal has cubic close packing for $B ^{-} . A ^{+}$is present in all octahedral voids. The edge length of the unit cell of the crystal $A B$ is ___$pm$. (Nearest Integer)

Answer: 512

Solution

$ a=2\left(r_{+}+r_{-}\right) $
$ a=2(102+181) $
$ a=2(283) $
$a=566\, pm$

Q23. The minimum uncertainty in the speed of an electron in an one dimensional region of length $2 a _0$
(Where $a _0=$ Bohr radius $52.9 \,pm$ ) is _____$km \,s ^{-1}$.
(Given : Mass of electron $=9.1 \times 10^{-31} kg$,
Planck's constant $h =6.63 \times 10^{-34} \,Js$ )

Answer: 548

Solution

Heisenberg's uncertainty principle
$ \Delta x \times \Delta p _{ x } \geq \frac{ h }{4 \pi} $
$ \Rightarrow 2 a _0 \times m \Delta v _{ x }=\frac{ h }{4 \pi}(\text { minimum })$
$ \Rightarrow \Delta v _{ x }=\frac{ h }{4 \pi} \times \frac{1}{2 a _0} \times \frac{1}{ m } $
$ =\frac{6.63 \times 10^{-34}}{4 \times 3.14 \times 2 \times 52.9 \times 10^{-12} \times 9.1 \times 10^{-31}}$
$ =548273\, ms ^{-1} $
$=548.273 \,km \,s ^{-1} $
$=548 \,km \,s ^{-1}$

Q24. When $600\, mL$ of $0.2 \, M\, HNO _3$ is mixed with $400 \, mL$ of $0.1 \, M \, NaOH$ solution in a flask, the rise in temperature of the flask is ___$\times 10^{-2}{ }^0 C$.
(Enthalpy of neutralisation $=57 \, kJ \, mol ^{-1}$ and Specific heat of water $=4.2 \, JK ^{-1}\, g ^{-1}$ )
(Neglect heat capacity of flask)

Answer: 54

Solution

image
$ \Delta_{ r } H =40 \,m \,mol \times\left(57 \times 10^3\right) \frac{ J }{ mol } $
$=40 \times 10^{-3}\, mol \times 57 \times 10^3 \frac{ J }{ mol }$
$= 2280 J $
$ m S \Delta T =2280$
$ \Rightarrow 1000 mL \times \frac{1 gm }{ mL } \times 4,2 \times \Delta T =2280
$
$\Delta T =\frac{2280}{4.2} \times 10^{-3} $
$=\frac{22800}{42} \times 10^{-3}$
$= 542.86 \times 10^{-3}$
$\Delta T =54.286 \times 10^{-2} K$
$\Delta T =54.286 \times 10^{-20} C$
Ans. $54.286$
Answer mentioned as 54 (Closest integer)

Q25. If $O _2$ gas is bubbled through water at $303\, K$, the number of millimoles of $O _2$ gas that dissolve in 1 litre of water is ____ (Nearest Integer)
(Given : Henry's Law constant for $O _2$ at $303 \,K$ is $46.82 \,k$ bar and partial pressure of $O _2=$ $0.920$ bar)
(Assume solubility of $O _2$ in water is too small, nearly negligible)

Answer: 1

Solution

$ p = K _{ H } \times x$
$ \underset{\text{bar}}{0.920}=46.82 \times 10^3 \text { bar } \times \frac{\text { mol of } O _2}{\text { mol of } H _2 O }$
image
$0.920=46.82 \times n _{ o _2}$
$p =\frac{0.920}{46.82 \times 18}= n _{0_2}$
$ \Rightarrow 1.09 \times 10^{-3}= n _{0_2}$
$ \Rightarrow\, m \,mol\, of _2=1$

Q26. If the solubility product of $PbS$ is $8 \times 10^{-28}$, then the solubility of $PbS$ in pure water at $298\, K$ is $x \times 10^{-16} \, mol\, L ^{-1}$. The value of $x$ is ___ . (Nearest Integer)
[Given $\sqrt{2}=1.41$ ]

Answer: 282

Solution

$ K _{ sp }= S ^2 $
$S =\sqrt{ K _{ sp }}=\sqrt{8 \times 10^{-28}}=2 \sqrt{2} \times 10^{-14}$
$ =2.82 \times 10^{-14} $
$ =282 \times 10^{-16} $
Ans. =$282$

Q27. The reaction between $X$ and $Y$ is first order with respect to $X$ and zero order with respect to $Y$.
Experiment $\frac{[ X ]}{ mol\, L ^{-1}}$ $\frac{[ Y ]}{ mol L ^{-1}}$ $\frac{\text { Initial rate }}{ mol L ^{-1} \min ^{-1}}$
I 0.1 0.1 $2 \times 10^{-3}$
II L 0.2 $4 \times 10^{-3}$
III 0.4 0.4 $M \times 10^{-3}$
IV 0.1 0.2 $2 \times 10^{-3}$

Examine the data of table and calculate ratio of numerical values of $M$ and $L$. (Nearest Inetger)

Answer: 40

Solution

$r = k [ x ][ y ]^0= k [ x ]$
Using I & II
$\frac{4 \times 10^{-3}}{2 \times 10^{-3}}=\left(\frac{ L }{0.1}\right) \Rightarrow L =0.2$
Using I & III
$ \frac{ M \times 10^{-3}}{2 \times 10^{-3}}=\frac{0.4}{0.1} \Rightarrow M =8$
$ \frac{ M }{ L }=\frac{8}{0.2}=40$
Ans. 40

Q28. In a linear tetrapeptide (Constituted with different amino acids), (number of amino acids) - (number of peptide bonds) is______.

Answer: 1

Solution

In Tetrapeptide,
No. of Amino Acids $= 4 $
No. of Peptide bonds $= 3 $
Hence
Ans. $= 1$

Q29. In bromination of Propyne, with Bromine 1, 1,2, 2-tetrabromopropane is obtained in $27\%$ yield. The amount of $1,1,2,2$ tetrabromopropane obtained from $1 g$ of Bromine in this reaction is ___$\times 10^{-1}\, g$. (Nearest integer)
(Molar Mass : Bromine $=80 \,g / mol )$

Answer: 3

Solution

image
$ =\frac{1}{160} \times \frac{1}{2} \times 360 \times 0.27 $
$ =0.30375 $
$ =3.0375 \times 10^{-1}$
$=3$

Q30. $\left[ Fe ( CN )_6\right]^{3-}$ should be an inner orbital complex. Ignoring the pairing energy, the value of crystal field stabilization energy for this complex is $(-)$ ____ $\Delta_0$. (Nearest integer)

Answer: 2

JEE Main Mathematics Question Paper with Solution 2022 July 29th Shift 1 - Morning

Q1. Let $R$ be a relation from the set $\{1,2$, $3 . \ldots \ldots \ldots, 60\}$ to itself such that $R =\{( a , b ): b = pq$, where $p , q \geq 3$ are prime numbers \}. Then, the number of elements in $R$ is :

A

600

B

660

C

540

D

720

Solution

Number of possible values of $a=60$, for $b=$ pq,
If $p =3, q =3,5,7,11,13,17,19$
If $p =5 q =5,7,11$
If $p =7 q =7$
Total cases $=60 \times 11=660$

Q2. If $z =2+3 i$, then $z ^5+(\bar{z})^5$ is equal to :

A

244

B

224

C

245

D

265

Solution

$ z^5+(\bar{z})^5=(2+3 i)^5+(2-3 i)^5 $
$ =2\left({ }^5 C_0 2^5+{ }^5 C_2 2^3(3 i)^2+{ }^5 C_4 2^1(3 i)^4\right) $
$ =2(32+10 \times 8(-9)+5 \times 2 \times 81)=244$

Q3. Let $A$ and $B$ be two $3 \times 3$ non-zero real matrices such that $AB$ is a zero matrix. Then

A

The system of linear equations $AX =0$ has a unique solution

B

The system of linear equations $AX =0$ has infinitely many solutions

C

$B$ is an invertible matrix

D

adj (A) is an invertible matrix

Solution

$ AB =0 \Rightarrow| AB |=0 $
image
If $|A| \neq 0, B=0$ (not possible)
If $| B | \neq 0, A =0$ (not possible)
Hence $| A |=| B |=0$
$\Rightarrow AX =0$ has infinitely many solutions

Q4. If $\frac{1}{(20-a)(40-a)}+\frac{1}{(40-a)(60-a)}+$ $\ldots \ldots+\frac{1}{(180-a)(200-a)}=\frac{1}{256}$, then the maximum value of $a$ is :

A

198

B

202

C

212

D

218

Solution

By splitting
$ \frac{1}{20}\left[\left(\frac{1}{20-a}-\frac{1}{40-a}\right)+\left(\frac{1}{40-a}-\frac{1}{60-a}\right)\right. $
$\left.+\ldots+\left(\frac{1}{180-a}-\frac{1}{200-a}\right)\right] $
$ \Rightarrow \frac{1}{20}\left(\frac{1}{20-a}-\frac{1}{200-a}\right)=\frac{1}{256} $
$(20-a)(200-a)=256 \times 9 $
$ a^2-220 a+1696=0 $
$a=8,212$
Hence maximum value of a is $212$ .

Q5. If $\displaystyle\lim _{x \rightarrow 0} \frac{\alpha e^x+\beta e^{-x}+\gamma \sin x}{x \sin ^2 x}=\frac{2}{3}$, where $\alpha, \beta, \gamma \in R$, then which of the following is NOT correct ?

A

$\alpha^2+\beta^2+\gamma^2=6$

B

$\alpha \beta+\beta \gamma+\gamma \alpha+1=0$

C

$\alpha \beta^2+\beta \gamma^2+\gamma \alpha^2+3=0$

D

$\alpha^2-\beta^2+\gamma^2=4$

Solution

$\displaystyle\lim _{x \rightarrow 0} \frac{\alpha\left(1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\ldots\right)+\beta\left(1-x+\frac{x^2}{2 !}-\frac{x^3}{3 !}+\ldots\right)+\gamma\left(x-\frac{x^3}{3 !}+\ldots\right)}{\left.x^3\right)}$
constant terms should be zero
$\Rightarrow a+\beta=0$
coeff of $x$ should be zero
$\Rightarrow \alpha-\beta+\gamma=0$
coeff of $x^2$ should be zero
$\displaystyle\lim _{x \rightarrow 0} \frac{x^3\left(\frac{\alpha}{3 !}-\frac{\beta}{3 !}-\frac{\gamma}{3 !}\right)+x^4\left(\frac{\alpha}{3 !}-\frac{\beta}{3 !}-\frac{\gamma}{3 !}\right)}{x^3}=\frac{2}{3}$
$ \Rightarrow \frac{\alpha}{2}+\frac{\beta}{2}=0 $
$ \frac{\alpha}{6}-\frac{\beta}{6}-\frac{\gamma}{6}=2 / 3$
$ \Rightarrow \alpha=1, \beta=-1, \gamma=-2$

Q6. The integral $\int\limits_0^{\frac{\pi}{2}} \frac{1}{3+2 \sin x+\cos x} d x$ is equal to:

A

$\tan ^{-1}(2)$

B

$\tan ^{-1}(2)-\frac{\pi}{4}$

C

$\frac{1}{2} \tan ^{-1}(2)-\frac{\pi}{8}$

D

$\frac{1}{2}$

Solution

$I=\int\limits_0^{\frac{\pi}{2}} \frac{d x}{3+2 \sin x+\cos x}=\int\limits_0^{\frac{\pi}{2}} \frac{\sec ^2 \frac{x}{2} \cdot d x}{2 \tan ^2 \frac{x}{2}+4 \tan \frac{x}{2}+4}$
Put $\tan \frac{x}{2}=t$, so
$I=\int\limits_0^1 \frac{d t}{(t+1)^2+1}=\left.\tan ^{-1}(x+1)\right|_0 ^1=\tan ^{-1} 2-\frac{\pi}{4}$

Q7. Let the solution curve $y=y$ (x) of the differential equation $\left(1+ e ^{2 x }\right)\left(\frac{ dy }{ dx }+ y \right)=1$ pass through the point $\left(0, \frac{\pi}{2}\right)$. Then, $\displaystyle\lim _{x \rightarrow \infty}$ $e ^{ x } y ( x )$ is equal to :

A

$\frac{\pi}{4}$

B

$\frac{3 \pi}{4}$

C

$\frac{\pi}{2}$

D

$\frac{3 \pi}{2}$

Solution

$\frac{d y}{d x}+y=\frac{1}{1+e^{2 x}}$
So integrating factor is $e^{\int 1 . d x}=e^x$
So solution is $y \cdot e^x=\tan ^{-1}\left(e^x\right)+c$
Now as curve is passing through
$ \left(0, \frac{\pi}{2}\right) \text { so } $
$ \Rightarrow c=\frac{\pi}{4} $
$ \Rightarrow \displaystyle\lim _{x \rightarrow \infty}\left(y \cdot e^x\right)= \displaystyle\lim _{x \rightarrow \infty}\left(\tan ^{-1}\left(e^x\right)+\frac{\pi}{4}\right)=\frac{3 \pi}{4}$

Q8. Let a line $L$ pass through the point of intersection of the lines $b x+10 y-8=0$ and $2 x-3 y=0, b \in R-\left\{\frac{4}{3}\right\}$. If the line $L$ also passes through the point $(1,1)$ and touches the circle $17\left(x^2+y^2\right)=16$, then the eccentricity of the ellipse $\frac{x^2}{5}+\frac{y^2}{b^2}=1$ is :

A

$\frac{2}{\sqrt{5}}$

B

$\sqrt{\frac{3}{5}}$

C

$\frac{1}{\sqrt{5}}$

D

$\sqrt{\frac{2}{5}}$

Solution

Line is passing through intersection of $b x+10 y-8=0$ and $2 x-3 y=0$ is $(b x+10 y-8)+\lambda(2 x-3 y)=0$. As line is passing through $(1,1)$ so $\lambda=b+2$
Now line $(3 b+4) x-(3 b-4) y-8=0$ is tangent to circle $17\left(x^2+y^2\right)=16$
$ \text { So } \frac{8}{\sqrt{(3 b+4)^2+(3 b-4)^2}}=\frac{4}{\sqrt{17}}$
$\Rightarrow b^2=2 \Rightarrow e=\sqrt{\frac{3}{5}}$

Q9. If the foot of the perpendicular from the point $A (-1,4,3)$ on the plane $P : 2 x + my + nz =$ 4 , is $\left(-2, \frac{7}{2}, \frac{3}{2}\right)$, then the distance of the point A from the plane $P$, measured parallel to a line with direction ratios $3,-1,-4$, is equal to :

A

1

B

$\sqrt{26}$

C

$2 \sqrt{2}$

D

$\sqrt{14}$

Solution

image
Let $B$ be foot of $\perp$ coordinates of $B =\left(-2, \frac{7}{2}, \frac{3}{2}\right)$
Direction ratio of line $AB$ is $\langle 2,1,3\rangle$ so $m=1, n=3$
So equation of $AC$ is $\frac{x+1}{3}=\frac{y-4}{-1}=\frac{z-3}{-4}=\lambda$
So point $C$ is $(3 \lambda-1,-\lambda+4,-4 \lambda+3)$. But
$C$ lies on the plane, so
$ 6 \lambda-2-\lambda+4-12 \lambda+9=4 $
$ \Rightarrow \lambda=1 \Rightarrow C(2,3,-1) $
$ \Rightarrow A C=\sqrt{26}$

Q10. Let $\vec{a}=3 \hat{i}+\hat{j}$ and $\vec{b}=\hat{i}+2 \hat{j}+\hat{k}$. Let $\vec{c}$ be a vector satisfying $\vec{a} \times(\vec{b} \times \vec{c})=\vec{b}+\lambda \vec{c}$. If $\vec{b}$ and $\vec{c}$ are non-parallel, then the value of $\lambda$ is:

A

$-5$

B

5

C

1

D

$-1$

Solution

$\vec{a}=3 \hat{i}+\hat{j}, \vec{b}=\hat{i}+2 \hat{j}+\hat{k}$
As $\vec{a} \times(\vec{b} \times \vec{c})=\vec{b}+\lambda \vec{c}$
$\Rightarrow \vec{a} \cdot \vec{c}(\vec{b})-(\vec{a} \cdot \vec{b}) \vec{c}=\vec{b}+\lambda \vec{c}$
$ \Rightarrow \vec{a} \cdot \vec{c}=1, \vec{a} \cdot \vec{b}=-\lambda $
$\Rightarrow(3 \hat{ i }+\hat{ j }) \cdot(\hat{ i }+2 \hat{ j }+\hat{ k })=-\lambda $
$ \Rightarrow \lambda=-5$

Q11. The angle of elevation of the top of a tower from a point A due north of it is $\alpha$ and from a point B at a distance of 9 units due west of A is $\cos ^{-1}\left(\frac{3}{\sqrt{13}}\right)$. If the distance of the point $B$ from the tower is 15 units, then $\cot \alpha$ is equal to :

A

$\frac{6}{5}$

B

$\frac{9}{5}$

C

$\frac{4}{3}$

D

$\frac{7}{3}$

Solution

image
given $OB =15$
$\cos \beta=\frac{3}{\sqrt{13}}$
image
$\tan \beta=\frac{2}{3}$
image
$\tan \beta=\frac{ h }{15}$
$\frac{2}{3}=\frac{h}{15} $
$ 10=h$
image
$OA ^2+ AB ^2=225 $
$OA ^2+81=225 $
$ OA =12$
image
$ \tan \alpha=\frac{10}{12} $
$ \cot \alpha=\frac{12}{10}=\frac{6}{5}$

Q12. The statement $(p \wedge q) \Rightarrow(p \wedge r)$ is equivalent to :

A

$q \Rightarrow(p \wedge r)$

B

$p \Rightarrow( p \wedge r )$

C

$( p \wedge r ) \Rightarrow( p \wedge q )$

D

$( p \wedge q ) \Rightarrow r$

Solution

$( p \wedge q ) \Rightarrow( p \wedge r ) $
$ \sim( p \wedge q ) \vee( p \wedge r ) $
$ (\sim p \vee \sim q ) \vee( p \wedge r )$
$ (\sim p \vee( p \wedge r )) \vee \sim q$
$ (\sim p \vee p ) \wedge(\sim p \vee r ) \vee \sim q $
$ (\sim p \vee r ) \vee \sim q $
$ (\sim p \vee \sim q ) \vee r $
$ \sim( p \wedge q ) \vee r $
$ ( p \wedge q ) \Rightarrow r $

Q13. Let the circumcentre of a triangle with vertices $A(a, 3), B(b, 5)$ and $C(a, b), a b>0$ be $P(1,1)$. If the line AP intersects the line $BC$ at the point $Q \left( k _1, k _2\right)$, then $k _1+ k _2$ is equal to :

A

2

B

$\frac{4}{7}$

C

$\frac{2}{7}$

D

4

Solution

image
$m _{ PD }=0 $
$ D \left(\frac{ a + a }{2}, \frac{ b +3}{2}\right)$
$ D \left( a , \frac{ b +3}{2}\right)$
$ m _{ PD }=0$
$ \frac{ b +3}{2}-1=0$
$ b +3-2=0 $
$ b =-1 $
$ E \left(\frac{ b + a }{2}, \frac{5+ b }{2}\right)=\left(\frac{ af }{2}, 2\right) $
$m _{ CB } \cdot m _{ EP }=-1$
$ \left(\frac{5-b}{b-a}\right)=\left(\frac{2-1}{a-1}\right)=-1 $
$\left(\frac{6}{-1-a}\right)=\left(\frac{2}{a-3}\right)=-1$
$12=(1+a)(a-3) $
$12=a^2-3 a+a-3$
$\Rightarrow a^2-2 a-15=0 $
$ (a-5)(a+3)=0 $
$a=5 \text { or } a=-3 $
$ \text { Given } a b>0 $
$ a(-1) >0 $
$ -a >0$
$ a< 0$
$ a =-3 \text { Accept }$
$\text { AP line A }(-3,3) P (1,1) $
$ y-1=\left(\frac{3-1}{-3-1}\right)(x-1) $
$ -2 y +2= x -1 $
$ \Rightarrow x+2 y=3 \text { Appling }......$(1)
$ \text { Line } B C B(-1,5) $
$ \text { C }(-3,-1) $
$ (y-5)=\frac{6}{2}(x+1) $
$ y-5=3 x+3 $
$ y=3 x+8 $....(2)
Solving (1) & (2)
$x+2(3 x+8)=3$
$ \Rightarrow 7 x+16=3$
$7 x =-13 $
$x=-\frac{13}{7}$
$ y=3\left(-\frac{13}{7}\right)+8 $
$ =\frac{-39+56}{7} $
$y=\frac{17}{7} $
$ x+y=\frac{-13+17}{7}=\frac{4}{7} $

Q14. Let $\hat{a}$ and $\hat{b}$ be two unit vectors such that the angle between them is $\frac{\pi}{4}$. If $\theta$ is the angle between the vectors $(\hat{a}+\hat{b})$ and $(\hat{a}+2 \hat{b}+2(\hat{a} \times \hat{b}))$, then the value of $164 \cos ^2 \theta$ is equal to :

A

$90+27 \sqrt{2}$

B

$45+18 \sqrt{2}$

C

$90+3 \sqrt{2}$

D

$54+90 \sqrt{2}$

Solution

Sol. $ \hat{a}^{\wedge} \hat{b}=\frac{\pi}{4}=\phi$
$\hat{a} \cdot \hat{b}=|\hat{a}||\hat{ b }| \cos \phi$
$\hat{a} \cdot \hat{b}=\cos \phi=\frac{1}{\sqrt{2}}$
$\cos \theta=\frac{(\hat{a}+\hat{b}) \cdot(\hat{a}+2 \hat{b}+2(\hat{a} \times \hat{b}))}{|\hat{a}+\hat{b}||\hat{a}+2 \hat{b}+2(\hat{a} \times \hat{b})|}$
$|\hat{a}+\hat{b}|^2=(\hat{a}+\hat{b}) \cdot(\hat{a}+\hat{b})$
$|\hat{a}+\hat{b}|^2=2+2 \hat{a} \cdot \hat{b}$
$=2+\sqrt{2}$
$\hat{a} \times \hat{b}=|\hat{a}||\hat{b}| \sin \phi \hat{n}$
$\hat{ a } \times \hat{ b }=\frac{\hat{ n }}{\sqrt{2}} \quad$
when $\hat{ n }$ is vector $\perp \hat{ a }$ and $\hat{ b }$
let $\overrightarrow{ c }=\hat{ a } \times \hat{ b }$
We know.
$ \vec{c} \cdot \vec{a}=0$
$ \vec{c} \cdot \vec{b}=0 $
$ |\hat{a}+2 \hat{b}+2 \vec{c}|^2 $
$ =1+4+\frac{(4)}{2}+4 \hat{a} \cdot \hat{b}+8 \hat{b} \cdot \vec{c}+4 \vec{c} \cdot \hat{a}$
$=7+\frac{4}{\sqrt{2}}=7+2 \sqrt{2}$
Now
$(\hat{a}+\hat{b}) \cdot(\hat{a}+2 \hat{b}+2 \vec{c})$
$ =|\hat{a}|^2+2 \hat{a} \cdot \hat{b}+0+\hat{b} \cdot \hat{a}+2|\hat{b}|^2+0$
$=1+\frac{2}{\sqrt{2}}+\frac{1}{\sqrt{2}}+2 $
$ =3+\frac{3}{\sqrt{2}}$
$ \cos \theta=\frac{3+\frac{3}{\sqrt{2}}}{\sqrt{2+\sqrt{2}} \sqrt{7+2 \sqrt{2}}} $
$ \cos ^2 \theta=\frac{9(\sqrt{2}+1)^2}{2(2+\sqrt{2})(7+2 \sqrt{2})}$
$ \cos ^2 \theta=\left(\frac{9}{2 \sqrt{2}}\right) \frac{(\sqrt{2}+1)}{(7+2 \sqrt{2})}$
$ 164 \cos ^2 \theta=\frac{(82)(9)}{\sqrt{2}} \frac{(\sqrt{2}+1)}{(7+2 \sqrt{2})} \frac{(7-2 \sqrt{2})}{(7-2 \sqrt{2})} $
$ =\frac{(82)}{\sqrt{2}} \frac{(9)[7 \sqrt{2}-4+7-2 \sqrt{2}]}{(41)}$
$ =(9 \sqrt{2})[5 \sqrt{2}+3]$
$ =90+27 \sqrt{2}$

Q15. If $f (\alpha)=\int\limits_1^\alpha \frac{\log _{10} t}{1+t} d t, \alpha>0$, then $f \left( e ^3\right)+ f$ $\left(e^{-3}\right)$ is equal to :

A

9

B

$\frac{9}{2}$

C

$\frac{9}{\log _e(10)}$

D

$\frac{9}{2 \log _c(10)}$

Solution

$ f \left( e ^3\right)=\int\limits_1^{ e ^3} \frac{\ell nt }{\ln 10(1+ t )} dt \ldots . . .(1) $
$ f (\alpha)=\int\limits_1^a \frac{\ell nt }{(\ln 10)(1+ t )} dt $
$ t =\frac{1}{ x } \Rightarrow x =\frac{1}{ t }$
$ dt =\frac{-1}{ x ^2} dx $
$=\int\limits_1^{\frac{1}{\alpha}} \frac{-\ell \ln x}{(\ell \ln 10)\left(1+\frac{1}{x}\right)}\left(-\frac{1}{x^2}\right) d x $
$ f(\alpha)=\frac{1}{\ell \ln 10} \int\limits_1^{\frac{1}{\alpha}} \frac{\ell nx }{ x ( x +1)} dx$
$ f \left( e ^{-3}\right)=\frac{1}{\ell \ln 10} \int\limits_1^{c^3} \frac{\ell nt }{ t ( t +1)} dt \ldots \ldots \ldots$
Add (1) & (2)
$f\left(e^3\right)+f\left(e^{-3}\right)$
$ =\left(\frac{1}{\ell n 10}\right) \int\limits_1^{ c ^3} \frac{\ell nt }{(1+ t )}\left[1+\frac{1}{ t }\right] dt $
$ =\left(\frac{1}{\ell n 10}\right) \int\limits_1^3 \frac{\ell nt }{ t } dt $
$ \ell nt = r $
$ \frac{ dt }{ t }= dr $
$ =\frac{1}{\ell n 10} \int\limits_0^3 rdr $
$ =\left.\left(\frac{1}{\ell n 10}\right)\left(\frac{ r ^2}{2}\right)\right|_0 ^3 $
$=\left(\frac{1}{\log 10}\right)\left(\frac{9}{2}\right)$
$ =\frac{9}{2 \log _{ e } 10}$

Q16. The area of the region $\left\{(x, y):|x-1| \leq y \leq \sqrt{5-x^2}\right\}$ is equal to :

A

$\frac{5}{2} \sin ^{-1}\left(\frac{3}{5}\right)-\frac{1}{2}$

B

$\frac{5 \pi}{4}-\frac{3}{2}$

C

$\frac{3 \pi}{4}+\frac{3}{2}$

D

$\frac{5 \pi}{4}-\frac{1}{2}$

Solution

image
$|x-1|< y< \sqrt{5-x^2}$
When $|x-1|=\sqrt{5-x^2}$
$ \Rightarrow(x-1)^2=5-x^2$
$\Rightarrow x^2-x-2=0 $
$ \Rightarrow x=2,-1$
Required Area $=$ Area of $\triangle ABC +$ Area of region $BCD$
$=\frac{1}{2}\begin{vmatrix}1 & 0 & 1 \\ 2 & 1 & 1 \\ -1 & 2 & 1\end{vmatrix}+\frac{\pi}{4}(\sqrt{5})^2-\frac{1}{2}(\sqrt{5})^2$
$=\frac{5 \pi}{4}-\frac{1}{2}$

Q17. Let the focal chord of the parabola $P : y ^2=4 x$ along the line $L : y = mx + c , m >0$ meet the parabola at the points $M$ and $N$. Let the line $L$ be a tangent to the hyperbola $H : x ^2- y ^2=4$. If $O$ is the vertex of $P$ and $F$ is the focus of $H$ on the positive $x$-axis, then the area of the quadrilateral $OMFN$ is :

A

$2 \sqrt{6}$

B

$2 \sqrt{14}$

C

$4 \sqrt{6}$

D

$4 \sqrt{14}$

Solution

image
$ O (0,0) $
$ H : \frac{ x ^2}{4}-\frac{ y ^2}{4}=1$
Focus (ae, 0)
$F (2 \sqrt{2}, 0)$
Line $L: y=m x+c$ pass $(1,0)$
$o = m + C$
Line $L$ is tangent to Hyperbola. $\frac{ x ^2}{4}-\frac{ y ^2}{4}=1$
$ C=\pm \sqrt{a^2 m^2-\ell^2} $
$ C=\pm \sqrt{4 m^2-4}$
From (1)
$-m=\pm \sqrt{4 m^2-4}$
Squaring
$m^2=4 m^2-4$
$ 4=3 m^2 $
$\frac{2}{\sqrt{3}}=m \quad(\text { as } m>0) $
$ C=-m$
$ C=\frac{-2}{\sqrt{3}} $
$ y =\frac{2 x }{\sqrt{3}}-\frac{2}{\sqrt{3}}$
$ y ^2=4 x$
$ \Rightarrow\left(\frac{2 x-2}{\sqrt{3}}\right)^2=4 x $
$\Rightarrow x ^2+1-2 x =3 x $
$ \Rightarrow x ^2-5 x +1=0$
$ y^2=4\left(\frac{\sqrt{3} y+2}{2}\right)$
$ y^2=2 \sqrt{3} y+4 $
$ \Rightarrow y^2-2 \sqrt{3} y-4=0$
Area
$ \left|\frac{1}{2}\right| \begin{vmatrix}0 & x _1 & 2 \sqrt{2} & x _2 & 0 \\0 & y _1 & 0 & y _2 & 0\end{vmatrix}||$
$=\left|\frac{1}{2}\left[-2 \sqrt{2} y _1+2 \sqrt{2} y _2\right]\right|$
$ =\sqrt{2}\left| y _2- y _1\right|=\frac{(\sqrt{2}) \sqrt{12+16}}{111}$
$ =\sqrt{56} $

Q18. The number of points, where the function $f : R \rightarrow R , f ( x )=| x -1| \cos | x -2| \sin | x -1|$ $+(x-3)\left|x^2-5 x+4\right|$, is NOT differentiable, is:

A

1

B

2

C

3

D

4

Solution

$f(x)=|x-1| \cos |x-2| \sin |x-1|+(x-3)\left|x^2-5 x+4\right|$
$ =|x-1| \cos |x-2| \sin |x-1|+(x-3)|x-1||x-4|$
$ =|x-1|[\cos |x-2| \sin |x-1|+(x-3)|x-4|]$
Non differentiable at $x=1$ and $x=4$.

Q19. Let $S=\{1,2,3, \ldots, 2022\}$. Then the probability, that a randomly chosen number $n$ from the set S such that $\operatorname{HCF}( n , 2022)=1$, is

A

$\frac{128}{1011}$

B

$\frac{166}{1011}$

C

$\frac{127}{337}$

D

$\frac{112}{337}$

Solution

Total number of elements $=2022$
$ 2022=2 \times 3 \times 337 $
$ \operatorname{HCF}( n , 2022)=1$
is feasible when the value of ' $n$ ' and 2022 has no common factor.
$A =$ Number which are divisible by 2 from $\{1,2,3 \ldots . .2022\}$
$n ( A )=1011$
$B=$ Number which are divisible by 3 by 3
from $\{1,2,3 \ldots \ldots 2022\}$
$n(B)=674$
$A \cap B=$ Number which are divisible by 6
from $\{1,2,3 \ldots \ldots . .2022\}$
$6,12,18 \ldots \ldots . ., 2022$
$337= n ( A \cap B )$
$n ( A \cup B )= n ( A )+ n ( B )- n ( A \cap B )$
$=1011+674-337$
$=1348$
$C =$ Number which divisible by 337 from $\{1, \ldots \ldots . .1022\}$
image
Total elements which are divisible by 2 or 3 or 337
$=1348+2=1350$
Favourable cases $=$ Element which are neither divisible by 2,3 or 337
$ =2022-1350$
$ =672$
Required probability $=\frac{672}{2022}=\frac{112}{337}$

Q20. Let $f(x)=3^{\left(x^2-2\right)^3+4}, x \in R$. Then which of the following statements are true ? $P : x =0$ is a point of local minima of $f$ $Q: x=\sqrt{2}$ is a point of inflection of $f$ $R$ : $f$ ' is increasing for $x>\sqrt{2}$

A

Only P and $Q$

B

Only P and R

C

Only Q and R

D

All, P, Q and R

Solution

$ f ( x )=81 \cdot 3^{\left( x ^2-2\right)^3} $
$f ^{\prime}( x )=81 \cdot 3^{\left( x ^2-2\right)^3} \cdot \ln 3 \cdot 3\left( x ^2-2\right)^2 \cdot 2 x$
$ =(81 \times 6) 3^{\left( x ^2-2\right)^3} \times\left( x ^2-2\right)^2 \ln 3$
image
$f ^{\prime}( x )=\underbrace{(486 \cdot \ln 3)}_{ k } \underbrace{3^{\left( x ^2-2\right)^3} x\left( x ^2-2\right)^2}_{ g ( x )}$
$g ^{\prime}( x )=3^{\left( x ^2-2\right)^3}\left( x ^2-2\right)^2+ x \cdot 3^{\left( x ^2-2\right)^3} \cdot 4 x \cdot\left( x ^2-2\right) $
$ + x \cdot\left( x ^2-2\right)^2 \cdot 3^{\left( x ^2-2\right)^3} \ln 3 \cdot 3\left( x ^2-2\right)^2 \cdot 2 x$
$ =3^{\left(x^2-2\right)^3}\left( x ^2-2\right)\left[ x ^2-2+4 x ^2+6 x ^2 \ln 3\left( x ^2-2\right)^3\right] $
$ g ^{\prime}( x )=3^{\left(x^2-2\right)^3}\left( x ^2-2\right)\left[5 x ^2-2+6 x ^2 \ln 3\left( x ^2-2\right)^3\right] $
$ f ^{\prime \prime}( x )= k \cdot g ^{\prime}( x )$
$f ^{\prime \prime}(\sqrt{2})=0, f ^{\prime \prime}\left(\sqrt{2}+>0, f ^{\prime}(\sqrt{2})<0\right. $
$ x^{-}=\sqrt{2} \text { is point of inflection }$
$ f ^{\prime \prime}( x ) >0 \text { for } x >\sqrt{2} \text { so } f ^{\prime}( x ) \text { is increasing }$

Q21. Let $S=\left\{\theta \in(0,2 \pi): 7 \cos ^2 \theta-3 \sin ^2 \theta-2\right.$ $\left.\cos ^2 2 \theta=2\right\}$. Then, the sum of roots of all the equations $x^2-2\left(\tan ^2 \theta+\cot ^2 \theta\right) x+6 \sin ^2 \theta=0$ $\theta \in S$, is

Answer: 16

Solution

$ 7 \cos ^2 \theta-3 \sin ^2 \theta-2 \cos ^2 2 \theta=2 $
$ 4 \cos ^2 \theta+3 \cos 2 \theta-2 \cos ^2 2 \theta=2$
$ 2(1+\cos 2 \theta)+3 \cos 2 \theta-2 \cos ^2 2 \theta=2 $
$ 2 \cos ^2 2 \theta-5 \cos 2 \theta=0$
$ \cos 2 \theta(2 \cos 2 \theta-5)=0 $
$ \cos 2 \theta=0$
$ 2 \theta=(2 n+1) \frac{\pi}{2} $
$ \theta=(2 n+1) \frac{\pi}{4} $
$ S=\left\{\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\right\}$
For all four values of $\theta$
$x^2-2\left(\tan ^2 \theta+\cot ^2 \theta\right) x+6 \sin ^2 \theta=0$
$\Rightarrow x^2-4 x+3=0$
Sum of roots of all four equations $=4 \times 4= 16.$

Q22. Let the mean and the variance of 20 observations $x _1, x _2, \ldots x _{20}$ be 15 and 9 , respectively. For $\alpha \in R$, if the mean of $\left( x _1+\alpha\right)^2,\left( x _2+\alpha\right)^2, \ldots,\left( x _{20}+\alpha\right)^2$ is 178 , then the square of the maximum value of $\alpha$ is equal to

Answer: 4

Solution

$\sum x_1=15 \times 20=300$...(i)
$ \frac{\sum x_1^2}{20}-(15)^2=9$...(ii)
$ \sum x_1^2=234 \times 20=4680 $
$ \frac{\sum\left(x_1+\alpha\right)^2}{20}=178 \Rightarrow \sum\left(x_1+\alpha\right)^2=3560$
$ \Rightarrow \sum x_1^2+2 \alpha \sum x_1+\sum \alpha^2=3560$
$ 4680+600 \alpha+20 \alpha^2=3560 $
$ \Rightarrow \alpha^2+30 \alpha+56=0 $
$ \Rightarrow(\alpha+28)(\alpha+2)=0 $
$\alpha=-2,-28$
Square of maximum value of $\alpha$ is 4

Q23. Let a line with direction ratios $a ,-4 a ,-7$ be perpendicular to the lines with direction ratios $3,-1,2 b$ and $b, a,-2$. If the point of intersection of the line $\frac{ x +1}{ a ^2+ b ^2}=\frac{ y -2}{ a ^2- b ^2}=\frac{ z }{1}$ and the plane $x-y+z=0$ is $(\alpha, \beta, \gamma)$, then $\alpha+\beta+\gamma$ is equal to

Answer: 10

Solution

$ (a,-4 a,-7) \perp \text { to }(3,-1,2 b) $
$ a=2 b$...(i)
$ (a,-4 a,-7) \perp \text { to }(b, a,-2) $
$ 3 a+4 a-14 b=0$
$a b-4 a^2+14=0$....(ii)
From Equations (i) and (ii)
$ 2 b^2-16 b^2+14=0$
$ b^2=1$
$ a^2=4 b^2=4 $
$ \frac{x+1}{5}=\frac{y-2}{3}=\frac{z}{1}=k $
$ \alpha=5 k-1, \beta=3 k+2, \gamma=k$
As $(\alpha, \beta, \gamma)$ satisfies $x-y+z=0$
$ 5 k -1-(3 k +2)+ k =0 $
$ k =1$
$ \therefore \alpha+\beta+\gamma=9 k +1=10$

Q24. Let $a_1, a_2, a_3, \ldots$ be an A.P. If $\displaystyle\sum_{r=1}^{\infty} \frac{a_r}{2^r}=4$, then $4 a_2$ is equal to

Answer: 16

Solution

$S=\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+\ldots$
$\frac{\frac{S}{2}=\frac{a_1}{2^2}+\frac{a_2}{2^3}+\ldots}{\frac{S}{2}=\frac{a_1}{2}+d\left(\frac{1}{2^2}+\frac{1}{2^3}+\ldots\right)}$
$ \frac{S}{2}=\frac{a_1}{2}+d\left(\frac{\frac{1}{4}}{1-\frac{1}{2}}\right) $
$ \therefore S=a_1+d=a_2=4$
Or $4 a_2=16$

Q25. Let the ratio of the fifth term from the beginning to the fifth term from the end in the binomial expansion of $\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^n$, in the increasing powers of $\frac{1}{\sqrt[4]{3}}$ be $\sqrt[4]{6}: 1$. If the sixth term from the beginning is $\frac{\alpha}{\sqrt[4]{3}}$, then $\alpha$ is equal to

Answer: 84

Solution

$ \frac{T_5}{T_{n-3}}=\frac{{ }^n C_4\left(2^{1 / 4}\right)^{n-4}\left(3^{-1 / 4}\right)^4}{{ }_{n-4}\left(2^{1 / 4}\right)^4\left(3^{-1 / 4}\right)^{n-4}}=\frac{\sqrt[4]{6}}{1}$
$ \Rightarrow 2^{\frac{n-8}{4}} 3^{\frac{n-8}{4}}=6^{1 / 4}$
$ \Rightarrow 6^{n-8}=6 $
$ \Rightarrow n-8=1 \Rightarrow n=9 $
$ T_6={ }^9 C_5\left(2^{1 / 4}\right)^4\left(3^{-1 / 4}\right)^5=\frac{84}{\sqrt[4]{3}} $
$ \therefore \alpha=84$

Q26. The number of matrices of order $3 \times 3$, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is

Answer: 282

Solution

$A =\begin{bmatrix} a _{11} & a _{12} & a _{13} \\ a _{21} & a _{22} & a _{23} \\ a _{31} & a _{32} & a _{33}\end{bmatrix}a _{ ij } \in\{0,1\}$
$ \sum a _{ ij }=2,3,5,7 $
Total matrix $={ }^9 C _2+{ }^9 C _3+{ }^9 C _5+{ }^9 C _7$
$=282$

Q27. Let $p$ and $p +2$ be prime numbers and let
$\Delta=\begin{vmatrix} p ! & (p+1) ! & (p+2) ! \\ (p+1) ! & (p+2) ! & (p+3) ! \\ (p+2) ! & (p+3) ! & (p+4) ! \end{vmatrix}$
Then the sum of the maximum values of $\alpha$ and $\beta$, such that $p ^\alpha$ and $( p +2)^\beta$ divide $\Delta$, is

Answer: 4

Solution

$\Delta=\begin{vmatrix}p ! & (p+1) ! & (p+2) ! \\(p+1) ! & (p+2) ! & (p+3) ! \\(p+2) ! & (p+3) ! & (p+4) !\end{vmatrix}$
$\Delta=P !(P+1) !( P +2) !\begin{vmatrix}1 & 1 & 1 \\ P +1 & P +2 & P +3 \\ ( P +2)( P +1) & ( P +3)( P +2) & ( P +4)( P +3)\end{vmatrix}$
$\Delta=2 P !( P +1) !( P +2) !$
Which is divisible by $P ^\alpha \&( P +2)^\beta$
$\therefore \alpha=3, \beta=1$

Q28. If $\frac{1}{2 \times 3 \times 4}+\frac{1}{3 \times 4 \times 5}+\frac{1}{4 \times 5 \times 6}+\ldots+$ $\frac{1}{100 \times 101 \times 102}=\frac{ k }{101}$, then $34 k$ is equal to

Answer: 286

Solution

$ \frac{1}{2.3 .4}+\frac{1}{3.4 .5}+\ldots . .+\frac{1}{100.101 .102}=\frac{ k }{101} $
$ \frac{4-2}{2.3 .4}+\frac{5-3}{3.4 .5}+\ldots . .+\frac{102-100}{100.101 .102}=\frac{2 k }{101}$
$ \frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+\ldots . .+\frac{1}{100.101}-\frac{1}{101.102}=\frac{2 k }{101}$
$ \frac{1}{2.3}-\frac{1}{101.102}=\frac{2 k }{101}$
$ \therefore 2 k =\frac{101}{6}-\frac{1}{102} $
$ \therefore 34 k =286$

Q29. Let $S=\{4,6,9\}$ and $T=\{9,10,11, \ldots$, 1000 . If $A =\left\{ a _1+ a _2+\ldots+ a _{ k }: k \in N , a _1, a _2\right.$, $\left.a_3, \ldots, a_k \in S\right\}$, then the sum of all the elements in the set $T - A$ is equal to

Answer: 11

Solution

$ S =\{4,6,9\} \quad T =\{9,10,11 \ldots .1000\} $
$A \left\{ a _1+ a _2+\ldots . .+ a _{ k }: K \in N \right\} \& a _{ i } \in S$
Here by the definition of set 'A'
$A=\{a: a=4 x+6 y+9 z\}$
Except the element 11, every element of set $T$ is of the form $4 x+6 y+9 z$ for some
$ x , y , z \in W$
$\therefore T - A =\{11\}$

Q30. Let the mirror image of a circle
$c_1: x^2+y^2-2 x-6 y+\alpha=0 \text { in line } y=x+1$
be $c_2: 5 x^2+5 y^2+10 g x+10 f y+38=0$.
If $r$ is the radius of circle $c_2$, then $\alpha+6 r ^2$ is equal to

Answer: 12

Solution

Image of centre $c_1 \equiv(1,3)$ in $x-y+1=0$ is given by
$ \frac{x_1-1}{1}=\frac{y_1-3}{-1}=\frac{-2(1-3+1)}{1^2+1^2} $
$\Rightarrow x_1=2, y_1=2$
$\therefore$ Centre of circle $c _2 \equiv(2,2)$
$\therefore$ Equation of $c _2$ be
$x^2+y^2-4 x-4 y+\frac{38}{5}=0$
Now radius of $c_2$ is $\sqrt{4+4-\frac{38}{5}}=\sqrt{\frac{2}{5}}=r$ $\left(\text { radius of } c_1\right)^2=\left(\text { radius of } c_2\right)^2$
$ \Rightarrow 10-\alpha=\frac{2}{5} \Rightarrow \alpha=\frac{48}{5} $
$ \therefore \alpha+6 r ^2=\frac{48}{5}+\frac{12}{5}=12$