KCET 2022 Physics Questions with Answers Key Solutions

Solution:

Stress $=$ Strain $\times Y$
Thus, maximum stress $=\frac{0.2}{100} \times 7 \times 10^{9}=1.4 \times 10^{7}$
Now, $F$ orce $=$ Stress $\times$ Area
Thus, $10^{4}=1.4 \times 10^{7} \times A$, or, $A =7.14 \times 10^{-4} m ^{2}$

Solution:

Here,
$
E =\frac{81 \pi}{7} \times 10^{5} V \textrm {m } ^ { - 1 }
$
$
v =2 \times 10^{-3} ms ^{-1}
$
$
\eta=1.8 \times 10^{5} N s m ^{-2}
$
$
\rho=900 kg m ^{-3}
$
When the electric field is switched off, let the drop falls with terminal velocity v , then
$
v =\frac{2 r ^{2}(\rho-\sigma) g}{9 \eta} \text { or } r=\left[\frac{9 v \eta}{2(\rho-\sigma) g}\right]^{\frac{1}{2}}
$
$
\therefore q=\frac{1}{E} \times \frac{4}{3} \pi \rho g\left[\frac{9 v \eta}{2(\rho-\sigma) g}\right]
$
$
=\frac{7}{81 \pi \times 10^{5}} \times \frac{4}{3} \times \pi \times 900 \times 9.8 \times\left[\frac{9 \times 8 \times 10^{-5} \times 2 \times 10^{-3}}{2 \times 900 \times 9.8}\right]^{\frac{3}{2}}
$
On solving we get, $q =8 \times 10^{-19} C$

Solution:

Mass of the chain lying freely from the table $= M \frac{1}{ L }$
$
\begin{array}{l}
=4 kg \times \frac{0.6}{2} \\
=1.2 kg
\end{array}
$
The distance of center of mass of chain from the table $=\frac{1}{2} \times 0.6 m =0.3 m$ Thus the work done in pulling the chain $=m g h=1.2 \times 10 \times 0.3 J =3.6 J$

Solution:

$\alpha=\frac{ W _{2}- W _{1}}{ t }=\frac{2 \pi n _{2}-2 \pi n _{1}}{ t }$

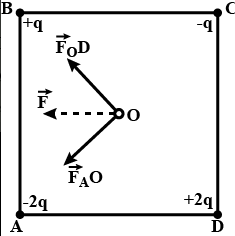
Solution:

Force due to charge at $D$ and $B$ is along $\overrightarrow{ F _{ O }} \overrightarrow{ D }$ towards $\overrightarrow{ B }$.
Force due to charge at $A$ and $C$ is along $\overrightarrow{ F _{ A } O }$ towards $\overrightarrow{ A }$.
$\therefore$ Resultant displacement will be along $\overrightarrow{ F }$ which is perpendicular to $AB$.

Solution:

$\tau=$ P.E. $\sin \theta$

Solution:

$K . E =\frac{1}{2} mv ^{2}$
$=\frac{1}{2} m \left(0+\frac{ Eq }{ m } t \right)^{2}$

Solution:

$E = K \frac{2 p }{ r ^{3}} \propto \frac{1}{ r ^{3}}$
$V = K \frac{ p \cos \theta}{ r ^{2}} \propto \frac{1}{ r ^{2}}$

Solution:

$A=3 \,m$
$V_{\max }=A \omega=3 \times 2 \pi=6 \pi$

Solution:

$\mu=\frac{V_{d}}{E} \Rightarrow V_{d}=\mu E$

Solution:

10 identical cells connected in series.
Potential of each cell $=E$
Internal resistance of each cell $=r$
Total voltage of ten cells $=10 E$
Total resistance of ten cells $=10 r$
Current in the circuit, $I=\frac{10 E}{10 r}=\frac{E}{r}$
Potentiol difference across 3 cells, $V=I \times 3 r$
$=\frac{E}{2} \times 3 r$
$=3 E$
Hence, ideal voltmeter will read $3 E$.

Solution:

$i =\frac{ e }{ T }= ef$

Solution:

$\frac{ R }{\ell}=\frac{ S }{100-\ell}$
If temperature increases, resistance increases.
As $R$ increases, balancing length also increases. It will shift towards Right

Solution:

$V =\frac{ kq _{1}}{ r _{1}}+\frac{ kq _{2}}{ r _{2}}$

Solution:

$B =\frac{\mu_{0} ni }{2}$

Solution:

$ R ^{\prime}=( n -1)( G + R ) $
$=\left(\frac{30}{20}-1\right) 3000=1500\, \Omega$
Total resistance $=2950+1500=4450\, \Omega$

Solution:

$B=\frac{\mu_{0} n i r^{2}}{2\left(x^{2}+r^{2}\right)^{3 / 2}}$

Solution:

$P =\frac{ V ^{2}}{ R }$
$P \propto V ^{2}$
$\frac{\Delta P }{ P } \times 100=2 \frac{\Delta V }{ V } \times 100$
$=2 \times 2.5=5 \%$

Solution:

Let $1_{1}=100,1_{2}=110$
$R \propto 1^{2}$
$\frac{ R _{2}}{ R _{1}}=\left(\frac{1_{2}}{1_{1}}\right)^{2}=\left(\frac{110}{100}\right)^{2}=1.21$
$ R _{2}=1.21 R _{1}$
Specific resistance remains same

Solution:

$\frac{1}{2} LI _{\max }^{2}=\frac{ q ^{2}}{2 C }$
$\frac{1}{2} LI ^{2}=\frac{1}{2} \times \frac{1}{2} LI _{\max }^{2}$
$I =\frac{ I _{\max }}{\sqrt{2}}$
$I _{\max } \sin \omega t =\frac{ I _{\max }}{\sqrt{2}}$
$\omega t =\frac{\pi}{4}$
$t =\frac{\pi}{4} \sqrt{ LC }$

Solution:

$\phi_{1}= BAN =1 \times 0.01 \times 80$
$\phi_{1}=0.8\, wb$
$\phi_{2}=0$
$e =-\frac{\left(\phi_{2}-\phi_{1}\right)}{ t }$
$=-\left(\frac{0-0.8}{2}\right)=4\, V$

Solution:

$i _{ rms }=\sqrt{\frac{ i _{1}^{2}+ i _{2}^{2}}{2}}$

Solution:

$\phi=500 \times 4 \times 10^{-3}=2 Wb$
$Li = N \phi$
$L =\frac{2}{2}=1 H$

Solution:

Micro waves

Solution:

$p=\frac{1}{f}=(\mu-1)\left(\frac{1}{-R}-\frac{1}{R}\right)$

Solution:

$i _{1}+ i _{2}- A = D$

Solution:

$u + v = x$
$m =\frac{ v }{ u }$
$\frac{1}{ v }-\frac{1}{ u }=\frac{1}{ f }$

Solution:

$f=\frac{1}{2 \pi \sqrt{L C}}$

Solution:

$Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}$

Solution:

$I \propto \frac{1}{ d ^{2}}$

Solution:

$\beta=\frac{\lambda D }{ d }, \frac{\beta_{1}}{\beta_{2}}=\frac{\lambda_{1}}{\lambda_{2}}$

Solution:

Solution:

$f \propto \frac{1}{(\mu-1)}, \mu_{ v } > \mu_{ r }$

Solution:

$\lambda \propto \frac{1}{\sqrt{ k }}$
$\frac{\lambda_{1}}{\lambda_{2}}=\sqrt{\frac{ k _{2}}{ k _{1}}},=\sqrt{\frac{ k }{4 k }}=\frac{1}{2}$
$\lambda_{2}=2 \lambda$

Solution:

$r \propto n ^{2}$
$\frac{ r _{1}}{ r _{2}}=\left(\frac{ n _{1}}{ n _{2}}\right)^{2}$
$0.25=\frac{1}{ n _{2}^{2}}$
$n _{2}^{2}=\frac{1}{0.25}=\frac{100}{25}=4$
$n _{2}=2$

Solution:

$m v_{0} r=n \frac{h}{2 \pi}$

Solution:

$r _{ n }=0.529 \times \frac{ n ^{2}}{ z } \,\,\,n =3$
$=0.529 \times 9=4.761 \,\mathring{A} $

Solution:

$BE =\left[ Zm _{ p }+( A - Z ) m _{ n }- m _{ X }\right] \times 931.5$
$Be =[7.05481+7.06069-14.0030] \times 931.5$
$=104.7\, MeV$

Solution:

$i \propto$ Intensity

Solution:

$KE _{1}- KE _{2}=\frac{ hc }{\lambda_{1}}-\frac{ hc }{\lambda_{2}}$
$\Delta KE = hc \left[\frac{1}{\lambda_{1}}-\frac{1}{\lambda_{2}}\right]$

Solution:

This is a case of AND gate. Input and output are shown below
$ \therefore y =\overline{\overline{ A }+\overline{ B }}=\overline{\overline{ A } \cdot \overline{ B }}= AB (\text { since } \overline{ A }+\overline{ B }=\overline{ A } \cdot \overline{ B }) $

Solution:

$F = Bil$
$Bil \cos \theta= mg \sin \theta$
$0.25 \times I \times \frac{\sqrt{3}}{2}=0.5 \times 10 \times \frac{1}{2}$
$I =\frac{5 \times 100}{25 \times \sqrt{3}}=\frac{20}{\sqrt{3}} A$
$I =11.32 \,A$

Solution:

$P =\frac{ E }{ t }=\frac{ mv ^{2}}{ t } \Rightarrow 10^{9}=\frac{ m \times 9 \times 10^{16}}{3600}$
$m =4 \times 10^{-5} kg$
$m =4 \times 10^{-5} \times 10^{3} g$
$m =4 \times 10^{-2} g$
$m =0.04 \,g$

Solution:

$\frac{ H _{1}}{ H _{2}}=\frac{\tan ^{2} \theta}{1}$

Solution:

$\tan \theta=\frac{V^{2}}{2 g}=\frac{10 \times 10}{10 \times 10}=1$
$\theta=\frac{\pi}{4}$

Solution:

$T _{1}=\left( m _{1}+ m _{2}\right)( g + a )$

Solution:

$L . C =1 MSD -1 VSD$
or L.C $=\frac{1 MSD }{\text { No.of.vernier scale division }}=\frac{0.05\, mm }{50}$
L.C $=0.01 \,mm$

Solution:

$
\begin{array}{l}
t=\sqrt{x}+3 \\
\Rightarrow x=(t-3)^{2}
\end{array}
$
$
\begin{array}{l}
v=\frac{d x}{d t}=2(t-3) \\
v=0 \Longrightarrow t=3
\end{array}
$
At $t=3, x=(3-3)^{2}=0$