JEE Main Physics Question Paper with Solution 2022 July 27th Shift 1 - Morning
A
$15 \%$
B
$25 \%$
C
$75 \%$
D
$5 \%$
Solution
Dimensional formula for Torque
$[\tau]=\left[ ML ^2 T ^{-2}\right]$
Now
Percentage error in torque $=\% \tau=\% M +2$
$\% L 2 \% T$
$\% \tau=25 \%$
A
1.25 W
B
2.5 W
C
6.25 W
D
12.5 W
Solution
Thrust $=\lambda V _{\text {rel }}$
$=2.5 N$
Now, Power $= F \times V =12.5 W$
A
2 m
B
0.5 m
C
3.2 m
D
0.8 ms
Solution
In frame of belt
$ a =\mu g =4 m / s ^2, v =2 m / s , u =0 $
$ v ^2= u ^2+2 as $
$\Rightarrow s =0.5 m$
A
0.25 J
B
1 J
C
8 J
D
12 J
Solution

$h =\frac{ h _1+ h _2}{2}$
Now,
$ W = U _{ i }- U _{ f } $
$ W =\left(\rho Ah _1\right) g \frac{ h _1}{2}+\left(\rho Ah _2\right) g \frac{ h _2}{2}-\rho$
$A \left( h _1+ h _2\right) g \left(\frac{ h _1+ h _2}{4}\right) $
$W =\frac{\rho Ag }{2}\left[ h _1^2+ h _2^2-\frac{\left( h _1+ h _2\right)^2}{2}\right] $
$ W =1 J $
A
$9: 16$
B
$16: 9$
C
$1: 1$
D
$4: 3$
Solution
Given that $\frac{ m _1}{ m _2}=\frac{4}{3}, \frac{ r _1}{ r _2}=\frac{3}{4}$
Now $TE =\frac{1}{2} mv ^2+\left(\frac{- GMm }{ r }\right)$
but $ \frac{ mv ^2}{ r }=\frac{ GMm }{ r ^2} \Rightarrow mv ^2=\frac{ GMm }{ r } $
$ \Rightarrow TE =-\frac{ GMm }{2 r } \propto \frac{ m }{ r } $
$ \frac{ TE _1}{ TE _2}=\frac{ m _1}{ m _2} \cdot \frac{ r _2}{ r _1}=\frac{4}{3} \times \frac{4}{3}=\frac{16}{9}$
A
$18^{\circ} C$
B
$14^{\circ} C$
C
$45^{\circ} C$
D
$150^{\circ} C$
Solution

$\frac{ d \theta}{ dt }=\frac{ K _1 A _1}{ l _1}\left( T _1- T \right)=\frac{ K _2 A _2}{ l _2}\left( T - T _2\right)$
$ \Rightarrow \frac{450- T }{ T -0}=\frac{ K _2 A _2 I _1}{ K _1 A _1 l _2}=9 \times \frac{1}{2} \times 2$
$\Rightarrow 450- T =9 T \Rightarrow T =45^{\circ} C$
A
A, B, C only
B
A, B only
C
A, C only
D
B, C, D only
Solution
Heat Transfer
A. by Newton's low of colling $\frac{ d \theta}{ dt }=\propto \Delta T$
B.$H =\frac{ d \theta}{ dt }=\sigma eAT ^4 \Rightarrow \frac{ H _{ r }}{ H _{ Q }}=\left(\frac{ T _{ r }}{ T _{ Q }}\right)^4=\left(\frac{283}{293}\right)^4$
$H_P: H_Q=1(1.03)^4=1:(1.03)^4=1: 1.15$
$\Rightarrow B$ is correct
C. $\eta=1-\frac{100}{400}=\frac{3}{4}=75 \%$
D. is wrong as $\frac{d \theta}{d t} \propto \Delta T$
A
A and C only
B
B and D only
C
A and B only
D
C and D only
Solution
KTG
A. $V _{ Rms }=\sqrt{\frac{3 R T }{ M _{ w }}} \Rightarrow V _{ Rms }$ is same
B. $\frac{ P _1}{ P _2}=\frac{ N _1}{ N _2} \Rightarrow B$ is correct
Ans [A & B only are correct]
A
$\sqrt{\frac{4 \pi^3 \varepsilon_0 m a^3}{q_0 Q}}$
B
$\sqrt{\frac{q_0 Q}{4 \pi^3 \varepsilon_0 m a^3}}$
C
$\sqrt{\frac{2 \pi^2 \varepsilon_0 m a^3}{q_0 Q}}$
D
$\sqrt{\frac{8 \pi^3 \varepsilon_0 m a^3}{q_0 Q}}$
Solution

$ F = macc { }^{ n }=\frac{ KQq _0}{( a - x )^2}-\frac{ KQq _0}{( a + x )^2}$
$m acc ^{ n }=\frac{ KQq _0[2 a ][2 x ]}{\left( a ^2- x ^2\right)^2}$
$\Rightarrow \operatorname{acc}^{ n } \approx\left(\frac{4 kQq_{0 } }{ ma ^3}\right) x$
$ T =2 \pi \sqrt{\frac{\pi \varepsilon_0 ma ^3}{ Qq _0}} $
$ T =\sqrt{\frac{4 \pi^3 \varepsilon_0 ma ^3}{ Qq _0}} $
A
$r_1-r_2$
B
$\frac{ r _1 r_2}{ r _1+r_2}$
C
$\frac{ r _1+r_2}{2}$
D
$r _2- r _1$
Solution

$ I =\frac{2 E }{ r _1+ r _2+ R } $
$ IR = E - Ir _2 $
$ I \left( R + r _2\right)= E $
$I =\frac{ E }{ R + r _2}$
$ \frac{2 E }{ r _1+ r _2+ R }=\frac{ E }{ R + r _2}$
$ 2 R +2 r _2= r _1+ r _2+ R $
$ R = r _1- r _2$
A
$2: 1$
B
$8: 3$
C
$1: 3$
D
$27: 16$
Solution
$T =2 \pi \sqrt{\frac{ I }{ MB _{ H }}} $
$ \frac{ T _1}{ T _2}=\frac{2 \pi \sqrt{\frac{ I _1}{ M _1 B _{ H }}}}{2 \pi \sqrt{\frac{ I _2}{ M _2 B _{ H }}}}=\frac{3}{4}$
$ \sqrt{\frac{ I _1}{ I _2} \times \frac{ M _2}{ M _1}}=\frac{3}{4} $
$ \sqrt{\frac{ I _1}{ I _2}} \times \sqrt{\frac{ M _2}{ M _1}}=\frac{3}{4} $
$\sqrt{\frac{3}{2}} \times \sqrt{\frac{ M _2}{ M _1}}=\frac{3}{4} $
$ \frac{3}{2} \times \frac{ M _2}{ M _1}=\frac{9}{16}$
$\frac{ M _1}{ M _2}=\frac{8}{3}$
A
$\tan ^{-1}\left(\sqrt{\frac{3}{2}}\right)$
B
$\tan ^{-1}(\sqrt{6})$
C
$\tan ^{-1}\left(\sqrt{\frac{2}{3}}\right)$
D
$\tan ^{-1}\left(\sqrt{\frac{1}{2}}\right)$
Solution
$ \tan \theta^{\prime}=\frac{\tan \theta}{\cos \alpha} $
$\theta^{\prime}=60^{\circ} $
$ \alpha=45^{\circ} $
$ \sqrt{3}=\frac{\tan \theta}{\frac{1}{\sqrt{2}}} $
$ \tan \theta=\sqrt{\frac{3}{2}} $
$ \theta=\tan ^{-1} \sqrt{\frac{3}{2}}$
A
$3: 2$
B
$3: 1$
C
$3: 4$
D
$4: 3$
Solution

$ H _1= i ^2 R _1 t \,\, H _2= i _{ rms }^2 R _2 t \left\{ i _{ rms }=\frac{ i _0}{\sqrt{2}}\right\}$
$ H _1=16(3) t \,\,H _2=\frac{ i _0^2}{2} R _2 t$
$ H _2=16 t$
$ H _1: H _2=3: 1$
A
$1: 1$
B
$1: 10$
C
$10: 1$
D
$1: 2$
Solution
$ E _{ y }=900 \sin \left(\omega t -\frac{\omega x }{ c }\right)$
$ E _0=900$

$F _{ E }= qE _0 $
$ F _{ B }= qvB _0$
$ \frac{ F _{ E }}{ F _{ B }}=\frac{ E _0}{ vB _0}=\frac{ c }{ v }=\frac{3 \times 10^8}{3 \times 10^7}=10: 1$
A
Resolving power will be $\frac{1}{4}$ in the oil than it was in the air
B
Resolving power will be twice in the oil than it was in the air.
C
Resolving power will be four times in the oil than it was in the air.
D
Resolving power will be $\frac{1}{2}$ in the oil than it was in the air.
Solution
$ (R.P )_{\text {air }}=\frac{2 \sin \theta}{1.22 \lambda} $
$(\text { R.P })_{\text {oil }}=\frac{2 \sin \theta}{1.22 \lambda_{\text {oil }}}=\frac{2 \sin \theta \times \mu}{1.22 \lambda}$
$ (\text { R.P })_{\text {oil }}=(\text { R.P })_{\text {air }} \times 2$
A
$\lambda_0$
B
$\lambda_0\left(1+\frac{ eE _0 t }{ mv _0}\right)$
C
$\lambda_0 t$
D
$\frac{\lambda_0}{\left(1+\frac{ eE _0 t }{ mv _0}\right)}$
Solution

$E =- E _0 \hat{ i } $
$ \lambda_0=\frac{ h }{ mv _0} $
$ v = v _0+\frac{ e E _0 t }{ m } $
$ \lambda=\frac{ h }{ mv }=\frac{ h }{ m \left( v _0+\frac{ eE _0}{ m } t \right)} $
$ \lambda^{\prime}=\frac{ h }{ mv _0\left(1+\frac{ eE }{ mv } t \right)}$
$ \lambda^{\prime}=\frac{\lambda_0}{\left(1+\frac{ eE _0}{ mv _0} t \right)}$
A
$9.5$ years
B
$8.5$ years
C
$7.5$ years
D
$10.5$ years
Solution
$ A = A _0 e ^{-\lambda t } $
$ \Rightarrow-\lambda t =\ln \left(\frac{ A }{ A _0}\right)$
$ \Rightarrow-\frac{\ln 2}{ t _{1 / 2}} \times 30=\ln \left(\frac{1}{16}\right) $
$\Rightarrow-\frac{\ln 2}{ t _{1 / 2}} \times 30=-4 \ln 2$
$ \Rightarrow t _{1 / 2}=\frac{30}{4}=7.5 \,yrs$
A
AND gate
B
OR gate
C
NOR gate
D
NAND gate
Solution


$\Rightarrow$ logic gate present is AND gate
A
200 m
B
300 m
C
600 m
D
900 m
Solution

I et d be range
$d ^2=( h + R )^2- R ^2$
$= h ^2+ R ^2+2 RH - R ^2$
$d ^2= h ^2+2 Rh$
as $R > > > > $ h then
$d \approx \sqrt{2 Rh } \ldots .(1)$
Now, if coverage is to be increased 3 times $3 d =\sqrt{2 Rh ^{\prime}} \ldots(2)$
Divide 2 and $1 \frac{3 d }{ d }=\sqrt{\frac{2 R h^{\prime}}{2 R h}}$
$9=\frac{h^{\prime}}{h}$
$9 h = h ^{\prime}$
If $h =100 m$ then tower of height $900 m$ is required
Answer: 2400
Solution
$ \frac{ S }{30}=\frac{5.6 \times 10^3}{70}$
$ S =\frac{3}{7} \times 5.6 \times 10^3=2400$
Answer: 412
Solution
$ 10 VSD =9 MSD $
$ 1 VST =.9 MSD$
$ \text { L.C. }=.1 mm =.01 \,cm $
$ \text { + ve zero error }=.4 \,mm$
$ =0.04\, cm$
Negative zero error $=4.1 \,cm +6 \times .01 $
$ =4.12 \,cm$
$ =412 \times 10^{-2} cm$
Answer: 2
Solution
$\phi_{ A }=\frac{\pi}{2} $
$ \phi_{ B }=\frac{\pi}{3} $
$I _{ A }= I +4 I +2 \sqrt{ I } \sqrt{4 I } \cos \left(\frac{\pi}{2}\right) $
$ =5 I +4 I (0)=5 I $
$ I _{ B }= I +4 I +2 \sqrt{ I } \sqrt{4 I } \cos \left(60^{\circ}\right) $
$ =5 I +4 I \times \frac{1}{2}=7 I $
$ I _{ B }- I _{ A }=7 I -5 I =2 I ,( x =2)$
Answer: 3
Solution
$P =\frac{ V ^2}{ R } \Rightarrow R =\frac{ V ^2}{ P }$

$ R =\frac{100 \times 10^2}{50}= R =200 \Omega$
$ V _{ R }^2+ V _{ C }^2= V ^2 $
$ (100)^2+ V _{ C }^2=(200)^2$
$ i =\frac{100}{200}=\frac{1}{2} ; V ^2=40000$
$V = I \times X _{ C } ; V _{ C }^2=30000$
$ V _{ C }=100 \sqrt{3} $
$ X _{ C }=200 \sqrt{3} $
$ 200 \sqrt{3}=\frac{1}{\omega C }$
$ C =\frac{1}{20 \times 50 \times 20 \sqrt{3}}=\frac{50 \times 10^{-6}}{\sqrt{ x }} $
$ \sqrt{ x }=50 \times 10^{-6} \times 100 \times 200 \sqrt{3} $
$X =3$
Answer: 136
Solution
$ l=1 m $
$ i =1 A$
Area $=2 \times 10^{-6} $
$ \rho=1.7 \times 10^{-8}$
$ R =\frac{\rho \ell}{ A }=\frac{1.7 \times 10^{-8} \times 1}{2 \times 10^{-5}}=\frac{1.7}{2} \times 10^{-2} $
$v =\frac{1.7}{2} \times 10^{-2} $
$ F =1.6 \times 10^{-19} \times \frac{1.7}{2} \times 10^{-2} $
$=1.36 \times 10^{-21}$
$ =136 \times 10^{-23}$
Answer: 1
Solution

$ \int E d s \cos 0=\frac{ q }{\varepsilon_0}$
$ \Rightarrow E \cdot 2 \pi xh =\frac{\rho \times \pi x ^2 h }{\varepsilon_0} $
$ \Rightarrow E =\frac{\rho x }{2 \varepsilon_0} $
$ \Rightarrow E=\frac{\rho}{2 \varepsilon_0} \times \frac{2 \varepsilon_0}{\rho}=1$
Answer: 16
Solution
$ \frac{1}{2} kA ^2=\frac{ p ^2}{2 m } $
$ \Rightarrow\left(\frac{ A _1}{ A _2}\right)^2=\frac{ m _2}{ m _1}=\frac{1024}{900} $
$ \Rightarrow \frac{ A _1}{ A _2}=\frac{32}{30}=\frac{16}{15}=\frac{16}{16-1} $
$ \therefore \alpha=16$
Answer: 48
Solution
$ \frac{ F }{ A }=\eta \frac{ x }{\ell} \Rightarrow \frac{ F \ell}{ A \eta}= x$
$ \Rightarrow x =\frac{18 \times 10^4 \times 60 \times 10^{-2}}{60 \times 10^{-2} \times 15 \times 10^{-2} \times 25 \times 10^9}$
$ =48 \times 10^{-6} m =48\, \mu m$
Answer: 18
Solution
$ \tau= I \alpha \Rightarrow\left(12 t -3 t ^2\right) 1.5=4.5 \alpha$
$\Rightarrow \alpha=4 t - t ^2 $
$ \Rightarrow \frac{ d \omega}{ dt }=4 t - t ^2 \Rightarrow \omega=\int_0^{ t }\left(4 t - t ^2\right) dt$
$ \Rightarrow \omega=2 t ^2- t ^3 / 3 $
For $ \omega=0=2 t ^2-\frac{ t ^3}{3} \Rightarrow t ^2\left(2-\frac{ t }{3}\right)=0 $
$ \Rightarrow t =0,6 $
$ \frac{ d \theta}{ dt }=2 t ^2-\frac{ t ^3}{3} \Rightarrow \theta=\int\limits_0^6\left(2 t ^2-\frac{ t ^3}{3}\right) dt $
$ =\left[\frac{2 t^3}{3}-\frac{t^4}{12}\right]_0^6$
$ =6^3\left(\frac{2}{3}-\frac{6}{12}\right)=6^3\left(\frac{8-6}{12}\right) $
$=\frac{6^3}{6}=36$
No. of revolutions $=\frac{36}{2 \pi}=\frac{18}{\pi}$
$\therefore K =18$
Answer: 1
Solution
Time of flight is same
$\Rightarrow$ vertical component of velocity is same
$\Rightarrow H _{\max }$ is same
JEE Main Chemistry Question Paper with Solution 2022 July 27th Shift 1 - Morning
A
$1.03$
B
$2.06$
C
$3.09$
D
$5.40$
Solution
$C _6 H _{12} O _6 \rightarrow \text { Glucose }$
We know: $\frac{\text { mass of } C }{\text { mass of glucose }}=\frac{72}{180}$
Given: $\% C =10.8=\frac{\text { mass of } C }{\text { mass of solution }} \times 100$ $\frac{10.8 \times 250}{100}=$ mass of $C \Rightarrow$ Mass of $C =27$
gm
$\therefore$ mass of glucose $=67.5 gm$
$\therefore$ moles of glucose $=0.375$ moles
Mass of solvent $=250-67.5 gm =182.5 gm$
$\therefore$ Molality $=\frac{0.375}{0.1825}=2.055 \approx 2.06$
A
Both Statement I and Statement II are correct.
B
Both Statement I and Statement II are incorrect.
C
Statement I is correct but Statement II is incorrect.
D
Statement I is incorrect but Statement II is correct.
Solution
$O _2, Cu ^{2+}$ and $Fe ^{3+}$ are paramagnetic,
$\therefore$ Weakly attracted by magnetic field.
$NaCl$ and $H _2 O$ are diamagnetic,
$\therefore$ Weakly repelled by magnetic field.
A
Both A and R are true and R is the correct explanation of A.
B
Both A and R are true but R is NOT the correct explanation of A.
C
A is true but R is false.
D
A is false but R is true
Solution
Energy of orbitals decreases on increasing the atomic number.
A
Both A and R are correct and R is the correct explanation of A.
B
Both A and R are correct but R is NOT the correct explanation of A.
C
A is correct but R is not correct.
D
A is not correct but R is correct.
Solution
$SO _2$ is absorbed to a greater extent than $CH _4$ on activated charcoal under same conditions. Gases with higher critical temperature are readily absorbed by activated charcoal.
A
$M _{ A }=4 M _{ B }$
B
$M _{ B }=4 M _{ A }$
C
$M _{ A }=8 M _{ B }$
D
$M _{ B }=8 M _{ A }$
Solution
For $A : 100\, gm$ solution $\rightarrow 2 \,gm$ solute A
$\therefore \text { Molality }=\frac{2 / M _{ A }}{0.098}$
For B : $100\,gm$ solution $\rightarrow 8$ gm solute B
$\therefore \text { Molality }=\frac{8 / M _{ B }}{0.092}$
$ \because\left(\Delta T _{ B }\right)_{ A }=\left(\Delta T _{ B }\right)_{ B }$
$ \therefore \text { Molality of } A =\text { Molality of } B$
$ \therefore \frac{2}{0.098 M _{ A }}=\frac{8}{0.092 M _{ B }} $
$ \frac{2}{98} \times \frac{92}{8}=\frac{ M _{ A }}{ M _{ B }} $
$ \frac{1}{4.261}=\frac{ M _{ A }}{ M _{ B }} $
$\therefore M _{ B }=4.261 \times M _{ A }$
A
The first ionization enthalpy of $K$ is less than that of $Na$ and $Li$
B
$Xe$ does not have the lowest first ionization enthalpy in its group
C
The first ionization enthalpy of element with atomic number 37 is lower than that of the element with atomic number 38 .
D
The first ionization enthalpy of Ga is higher than that of the d-block element with atomic number 30 .
Solution
Ionization enthalpy order :
$ Li > Na > K $
$ He > Ne > Ar > Kr > Xe > Rn$
$ Sr > Rb$
$ Zn > Ga $
A
B and D only
B
A, B, D and E only
C
B, D and E only
D
A, C and E only
Solution
Calcination and leaching are the methods of concentration of ore and not that of refining.
A
Both statement I and Statement II are ture
B
Both statement I and Statement II are false
C
Statement I is true but Statement II is false
D
Statement I is false but Statement II is true
Solution
Depending on the nature of reducing agent $H _2 O _2$ can act as an oxidising agent in both acidic as well as basic medium.
Density of $D _2 O =1.1\, g / cc$
Density of $H _2 O _2=1.45\, g / cc$
A
Both statement I and Statement II are true
B
Both statement I and Statement II are false
C
Statement I is true but Statement II is false
D
Statement I is false but Statement II is true
Solution
$Be _2 Cl _4$ is lewis acid and $Al _2 Cl _6$ has complete octet. $Be$ and $Al$ are amphoteric metals therefore dissolve in acid as well as alkaline solution and form beryllate and aluminate ions in excess alkali.
A
Pyrophosphorous acid
B
Hypophosphoric acid
C
Phosphoric acid
D
Pyrophosphoric acid
Solution
Pyrophosphorous acid $\rightarrow H _4 P _2 O _5$.
Hypophosphoric acid $\rightarrow H _4 P _2 O _6$.
Phosphoric acid $\rightarrow H _3 PO _4$.
Pyrophosphoric acid $\rightarrow H _4 P _2 O _7$.
A
Both statement I and Statement II are ture
B
Both statement I and Statement II are false
C
Statement I is true but Statement II is false
D
Statement I is false but Statement II is true
Solution
Neutral $KMnO _4$ oxidises $I ^{-}$to $IO _3^{-}$
Manganate ion has $d \pi- p \pi$ bonding.
A
A-IV, B -I, C-II, D-III
B
A-III, B -I, C-IV, D-II
C
A-II, B -IV, C-I, D-III
D
A-II, B -IV, C-III, D-I
Solution
A. Sulphate ( $>500\, ppm )$ - Causes Laxative effect that leads to dehydration
B. Nitrate ( $>50\, ppm )$ - Causes
Methemoglobinemia, skin appears blue
C. Lead $(>50 \,ppb)$ - It damage kidney and RBC
D. Fluoride ( $>2 \,ppm )$ - It Causes Brown mottling of teeth
A
Both A and R are correct and R is the correct explanation of A.
B
Both A and R are correct but R is NOT the correct explanation of A.
C
A is correct but R is not correct.
D
A is not correct but R is correct.
Solution
Assertion A : Not correct , Reason R : correct

In [10] -Annulene - the hydrogen atoms in the 1 and 6 position interfere with each other and force the molecule out of planarity

If this annulene with five cis double bonds were planar, each internal angle would be $144^{\circ}$. Since a normal double bond has bond angle of $120^{\circ}$, this would be from ideal. This compound can be made but it does not adopt a planar conformation and therefore is not aromatic even though it has ten $\pi$ electrons.
A
A-II, B -III, C-IV, D-I
B
A-II, B -III, C-I, D-IV
C
A-II, B -I, C-III, D-IV
D
A-III, B -II, C-IV, D-I
Solution

 ,
,
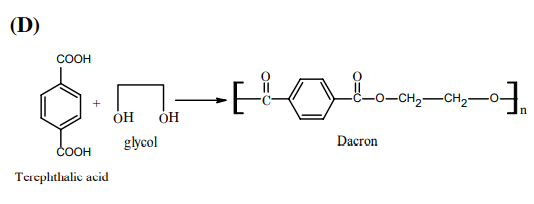
A
Aldopentose
B
Aldotetrose
C
Oxalic acid
D
Ketotetrose
A
A-IV, B -III, C-II, D-I
B
A-III, B -I, C-II, D-IV
C
A-III, B -IV, C-I, D-II
D
A-III, B -I, C-IV, D-II
Solution

It is morphine use for relief for pain, known for narcotic analgesic 
A
$34.04 \%$
B
$40.04 \%$
C
$36.03 \%$
D
$38.04 \%$
Solution
Mass of organic compound $=0.45 \,gm$
Mass of $AgBr$ obtained $=0.36 \,gm$
$\therefore \text { Moles of } AgBr =\frac{0.36}{188}$
$ \therefore $ Mass of Bromine
$ =\frac{0.36}{188} \times 80=0.1532 \,gm $
$\therefore \% Br $ in compound
$ =\frac{0.1532}{0.45} \times 100=34.04 \%$
A
A-IV, B -III, C-II, D-I
B
A-IV, B -II, C-I, D-III
C
A-III, B -IV, C-I, D-II
D
A-IV, B -III, C-I, D-II
Solution

Benzen sulphonyl chloride
(B) Hoffmann bromamide reaction $\rightarrow$ known reaction of isocynates
$R - CO - NH _2+ X _2+4 NaOH \rightarrow$
$ R - NH _2+2 NaX _2+ Na _2 CO _3+2 H _2 O$
Intermediate $: R - N = C = O$ (isocyanat
(C) Carbylamine reaction $\rightarrow$ Test for primary amine
$R - NH _2$ or $Ar - NH _2+ CHCl _3+3 KOH$
$\rightarrow RNC$ or $Ar - NC +3 KCl +3 H _2 O$
(D) Hoffmann orientation $\rightarrow$ Anti saytzeff (Formation of less substituted alkene as major product)
Answer: 24
Solution
Eq. of $K _2 Cr _2 O _7=$ Eq. of $Fe ^{2+}$
$\Rightarrow \left(\text { Molarity } \times \text { volume } \times \text { n.f) of } K _2 Cr _2 O _7\right. $
$ =(\text { molarity } \times \text { volume } \times \text { n.f }) \text { of } Fe ^{2+} $
$\Rightarrow 0.02 \times 20 \times 6= M \times 10 \times 1 $
$\Rightarrow M =0.24 $
$\Rightarrow \text { Molarity }=24 \times 10^{-2}$
Answer: 2
Solution
On decreasing pressure of $NO$ by a factor of ' 2 ' the rate of reaction decreases by a factor of '4'.
$\therefore$ Order of reaction w.r.t. ' $NO$ ' $=2$
Answer: 4
Solution
$KO _2, NO _2, ClO _2, NO$ are paramagnetic.
Answer: 2
Solution
$C _{ p , m }= C _{ v , m }+ R$
$ \Rightarrow C _{ v , m }=20.785-8.314=12.471 J k ^{-1} ml ^{-1} $
$ \Delta U = nC _{ v , m } \Delta T$
$ \Rightarrow n =\frac{5000}{12.471 \times 200}=\frac{25}{12.471} \approx 2$
Answer: 3
Solution
$CN ^{-}, NO ^{+}, O _2^{2+}$ have bond order $=3$
Answer: 0
Solution
Solubility of $CaF _2= S$ mole $/ L$
$S =\frac{2.34 \times 10^{-3}}{0.1 \times 78}=\frac{2.34}{78} \times 10^{-2}=3 \times 10^{-4} mol / L$
$ K _{\text {sp }}\left( CaF _2\right)=4 S ^3=4\left(3 \times 10^{-4}\right)^3$
$=108 \times 10^{-12} $
$ =0.0108 \times 10^{-8}( mol / L )^3$
Answer: 3
Solution
$\left[ Co \left( NH _3\right)_4 Cl _2\right] Cl$
Primary valency $=$ oxidation no. $=+3$
Answer: 1
Solution
Oxidation state of carbon changes from $+3$ to $+4$.
$ 2 KMnO _4+5 H _2 C _2 O _4+3 H _2 SO _4 \text { (dil.) } \rightarrow $
$ K _2 SO _4+2 MnSO _4+10 CO _2+8 H _2 O$
Answer: 42
Solution
$\%$ optical purity
$=\frac{\text { observed rotation of mixture } \times 100}{\text { rotation of pure enantiomer }} $
$=\frac{+12.6^{\circ}}{+30^{\circ}} \times 100=42$
Answer: 30
Solution

Let initial moles of reactant taken $= n$
Total moles obtained for benzene sulphonic acid $($ with $\%$ yield $=60 \%)=0.6 n$

Moles of benzene sulphonic acid before reaction II $=0.6 n$
Moles obtained for phenol (with $\%$ yield $=50 \%$ ) $=0.6 \times 0.5 n =0.3 n$
So over all \% yield of complete reaction $=\frac{0.3 n }{ n } \times 100=30$
JEE Main Mathematics Question Paper with Solution 2022 July 27th Shift 1 - Morning
A
$R_1$ is an equivalence relation but not $R_2$
B
$R_2$ is an equivalence relation but not $R_1$
C
both $R_1$ and $R_2$ are equivalence relations
D
neither $R_1$ nor $R_2$ is an equivalence relation
Solution
$R_1=\{x y \geq 0, x, y \in R\}$
For reflexive $x \times x \geq 0$ which is true.
For symmetric
If $x y \geq 0 \Rightarrow y x \geq 0$
If $x=2, y=0$ and $z=-2$
Then $x \cdot y \geq 0 \& y \cdot z \geq 0$ but $x . z \geq 0$ is not true
$\Rightarrow$ not transitive relation.
$\Rightarrow R_1$ is not equivalence
$R _2$ if $a \geq b$ it does not implies $b \geq a$
$\Rightarrow R_2$ is not equivalence relation
$\Rightarrow D$
A
one-one but not onto
B
onto but not one-one
C
both one-one and onto
D
neither one-one nor onto
Solution
$f : N -\{1\} \rightarrow N f ( a )=\alpha$
Where $\alpha$ is max of powers of prime $P$
such that $p ^\alpha$ divides $a$. Also $g ( a )= a +1$
$ \therefore f (2)=1 $
$ f (3)=1 $
$ f (4)=2 $
$ f (5)=1$
$g (2)=3 $
$ g (3)=4$
$ g (4)=5$
$g (5)=6$
$\Rightarrow f (2)+ g (2)=4 $
$ ( f (3)+ g (3))=5 $
$ f (4)+ g (4)=7$
$ f (5)+ g (5)=7 $
$ \therefore $ Many one }$f ( x )+ g ( x ) $ does not cotain $1 $
$ \Rightarrow $ into function
$ \therefore $ Ans. (D) [neither one-one nor onto ]
A
1000
B
1024
C
1105
D
1196
Solution
$z _0=\left(\frac{0+3+0}{3}, \frac{0+6+0}{3}\right)=(1,2)$
$ v_0=|1+2 i|^2+|1+2 i-3|^2+|1+2 i-6 i|^2=30$
Then $\left|2 z_0^2-\bar{z}_0^3+3\right|^2+v_0^2$
$ =\left|2(1+2 i)^2-(1-2 i)^3+3\right|^2+900 $
$ =|2(1-4+4 i)-(1-4-4 i)(1-2 i)+3|^2+900 $
$ =|8+6 i|^2+900=100+900=1000$
A
$-10$
B
$-6$
C
6
D
10
Solution
Characteristic equation of matric A
$ | A -\lambda I |=0 $
$ \begin{vmatrix} 1-\lambda & 2 \\-2 & -5-\lambda\end{vmatrix}=0 $
$\Rightarrow \lambda^2+4 \lambda=1 $
$ \Rightarrow A ^2+4 A = I $
$ \Rightarrow 2 A ^2+8 A =2 I ....$(1)
Given that $\alpha A ^2+\beta A =2 I.....$(2)
Comparing equation (1) & (2) we get
$\alpha=2, \beta=8$
$ \therefore \alpha+\beta=10$
Ans. (D) (10)
A
0
B
1
C
2
D
6
Solution
$ (2021)^{2022}+(2022)^{2021}$
$=(2023-2)^{2022}+(2023-1)^{2021} $
$ =7 n _1+2^{2022}+7 n _2-1 $
$ =7\left( n _1+ n _2\right)+8^{674}-1 $
$ =7\left(n_1+n_2\right)+(7-1)^{674}-1 $
$=7\left(n_1+n_2\right)+7 n_3+1-1$
$ =7\left( n _1+ n _2+ n _3\right)$
$\therefore$ Given number is divisible by 7 hence remainder is zero
A
290
B
380
C
460
D
510
Solution
$ \frac{ S _5}{ S _9}=\frac{5}{17} \Rightarrow \frac{\frac{5}{2}(2 a +4 d )}{\frac{9}{2}(2 a +8 d )}=\frac{5}{17} $
$\Rightarrow d =4 a$
$ a _{15}= a +14 d =57 a$
Now $, 110< a _{15}<120 $
$ \Rightarrow 110<57 a <120$
$ \Rightarrow a =2 \therefore d =8 $
$ S _{10}=\frac{10}{2}(2 \times 2+9 \times 8)=380$
A
$-1$
B
$-2$
C
1
D
2
Solution
$\displaystyle\lim _{x \rightarrow-1^{+}} a \sin \left(\pi \frac{[x]}{2}\right)+[2-x]=-a+2$
$ \displaystyle\lim _{x \rightarrow-1^{-}} a \sin \left(\pi \frac{[x]}{2}\right)+[2-x]= $
$\displaystyle\lim _{x \rightarrow-1} f(x) \text { exist when } a=-1$
Now,
$ \int\limits_0^4 f(x) d x=\int\limits_0^1 f(x) d x+\int\limits_1^2 f(x) d x+\int\limits_2^3 f(x) d x+\int\limits_3^4 f(x) d x $
$ =\int\limits_0^1(0+1) d x+\int\limits_1^2(-1+0) d x+\int\limits_2^3(0-1) d x+$
$ \int\limits_3^4(1-2) d x $
$ =1-1-1-1=-2$
A
$\frac{\pi}{2}
B
$\frac{\pi}{5}
C
$\frac{5 \pi}{12}
D
$\frac{3 \pi}{4}
Solution
Consider
$ f(x)=8 \sin x-\sin 2 x$
$ f^{\prime}(x)=8 \sin x-2 \cos 2 x $
$ f^{\prime}(x)=-8 \sin x+4 \sin 2 x $
$ =-8 \sin x(1-\cos x)$
$ \therefore f^{\prime}(x)<0 x \in\left(\frac{\pi}{4}, \frac{\pi}{3}\right)$
$\therefore f ^{\prime}( x )$ is $\downarrow$ function
$f ^{\prime}\left(\frac{\pi}{3}\right)< f ^{\prime}( x )< f ^{\prime}\left(\frac{\pi}{4}\right)$
$ 5< f ^{\prime}( x )<\frac{8}{\sqrt{2}}$
$ 5< f ^{\prime}( x )<4 \sqrt{2}$
$ 5 x < f ( x )<4 \sqrt{2} x $
$5<\frac{ f ( x )}{ x }<4 \sqrt{2} $
$ \int\limits_{\pi / 4}^{\pi / 3} 5<\int \frac{ f ( x )}{ x }<\int\limits_{\pi / 4}^{\pi / 3} 4 \sqrt{2} $
$ \int\limits_{\pi / 4}^{\pi / 3} 5<\int \frac{8 \sin x -\sin 2 x}{ x }<\int\limits_{\pi / 4}^{\pi / 3} 4 \sqrt{2} $
$ \frac{5 \pi}{12}< I <\frac{\sqrt{2} \pi}{3}$
A
$\frac{1}{3}(2-12 \sqrt{3}+8 \pi)$
B
$\frac{1}{3}(2-12 \sqrt{3}+6 \pi)$
C
$\frac{1}{3}(4-12 \sqrt{3}+8 \pi)$
D
$\frac{1}{3}(4-12 \sqrt{3}+6 \pi)$
Solution

$x^2+y^2+4 \sqrt{3} x-4=0$
$ y^2=8 x+4$
Point of intersections are $(0,2) \&(0,-2)$ Both are symmetric about $x$-axis Area $=2 \int\limits_0^2\left(\sqrt{16-y^2}-2 \sqrt{3}\right)-\left(\frac{y^2-4}{8}\right) d y$ On solving Area $=\frac{1}{3}[8 \pi+4-12 \sqrt{3}]$
A
0
B
1
C
2
D
3
Solution
$ \frac{d y}{d x}=x+y \Rightarrow \frac{d y}{d x}-y=x$
$ \therefore \text { solution is } y e^{-x}=\int x e^{-x} d x $
$ \Rightarrow y e^{-x}=-x e^{-x}-e^{-x}+c $
$\Rightarrow y=-x-1+c e^x $
$ y_1(0)=0 \Rightarrow c=1 $
$ \therefore y_1=-x-1+e^x ....$(1)
$ y _2(0)=1 \Rightarrow c =2$
$ \therefore y_2=-x-1+2 e^x .....$(2)
Now $y_2-y_1=e^x>0 \therefore y_2 \neq y_1$
$\therefore$ Number of points of intersection of $y _1 \& y _2$ is zero.
A
0
B
25
C
40
D
65
Solution
$P ( a , b )$ is point on $y ^2=8 x$, such that tangent at $P$ pass through centre of $x^2+y^2-10 x-$ $14 y +65=0$ i.e. $(5,7)$
Tangent at $P \left( at ^2, 2 at \right)$ is ty $= x + at ^2$
$A =2 \&$ it pass through $(5,7)$
$7 t=5+2 t^2$
$ \Rightarrow t=1, t=\frac{5}{2}$
$ \therefore P\left(a t^2, 2 a t\right) \Rightarrow(2,4) \text { when } t =1 $
$\left(\frac{25}{2}, 10\right) \text { when } t=\frac{5}{2}$
$ \therefore A=2 \times \frac{25}{2}=25 $
$B =4 \times 10=40 \therefore A+B=65$
A
2
B
$\frac{39}{5}$
C
9
D
$\frac{46}{5}$
Solution
Let $ \vec{a}=\alpha \hat{i}+\hat{j}+\beta \hat{k}, \vec{b}=3 \hat{i}-5 \hat{j}+4 \hat{k} $
$\vec{a} \times \vec{b}=-\hat{i}+9 \hat{j}+12 \hat{k} $
$\Rightarrow \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ \alpha & 1 & \beta \\ 3 & -5 & 4\end{vmatrix} $
$ \Rightarrow(4+5 \beta) \hat{i}+(3 \beta-4 \alpha) \hat{j}+(-5 \alpha-3) \hat{k} $
$ =-\hat{i}+9 \hat{j}+12 \hat{k} $
$ \therefore 4+5 \beta=-1,3 \beta-4 \alpha=9,-5 \alpha-3=12 $
$ \beta=-1, \alpha=-3$
$ \therefore \vec{a}=-3 \hat{i}+\hat{j}-\hat{k}, \vec{b}=3 \hat{i}-5 \hat{j}+4 \hat{k} $
$ \therefore \vec{a}+\vec{b}=-4 \hat{j}+3 \hat{k} $
$|\vec{a}|^2=11,|\vec{b}|^2=50$
$\vec{a} \cdot \vec{b}=-9+(-5)-4=-18$
$\therefore$ Projectile of $(\vec{b}-2 \vec{a})$ on $\vec{a}+\vec{b}$ is
$\frac{(\vec{b}-2 \vec{a}) \cdot(\vec{a}+\vec{b})}{|\vec{a}+\vec{b}|}$
$=\frac{|\vec{b}|^2-2|\vec{a}|^2-(\vec{a} \cdot \vec{b})}{|\vec{a}+\vec{b}|}=\frac{50-22-(-18)}{5}=\frac{46}{5}$
Ans. $\left(\frac{46}{5}\right)$
A
4
B
5
C
$\sqrt{21}$
D
$\sqrt{17}$
Solution
$ \vec{a}=2 \hat{i}-\hat{j}+5 \hat{k}, \vec{b}=\alpha \hat{i}+\beta \hat{j}+2 \hat{k} $
$ ((\vec{a} \times \vec{b}) \times \hat{i}) \cdot \hat{k}=\frac{23}{2}, \text { then }|\vec{b} \times 2 \hat{j}| \text { is }$
$ ((\vec{a} \cdot \hat{i}) \vec{b}-(\vec{b} \cdot \hat{i}) \vec{a}) \cdot \hat{k}=\frac{23}{2}$
$ (\vec{a} \cdot \hat{i})(\vec{b} \cdot \hat{i})-(\vec{b} \cdot \hat{i})(\vec{a} \cdot \hat{k})=\frac{23}{2}$
$2 \times 2-\alpha \times 5=\frac{23}{2} \Rightarrow 5 \alpha=4-\frac{23}{2} \Rightarrow \alpha=\frac{-3}{2} $
$ \vec{b} \times 2 \hat{j}= \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 0 & \beta & 2 \\ 0 & 2 & 0\end{vmatrix}$
$=-4 \hat{i}+2 \alpha \hat{k}$
$ \therefore|\vec{b} \times 2 \hat{j}|=\sqrt{16+4 \alpha^2}=\sqrt{16+4 \times \frac{9}{4}}=5$
A
$1.0146$
B
$1.2085$
C
$1.0285$
D
$1.1521$
Solution
$n ( S )=$ all 5 digit $\operatorname{nos}=9 \times 10^4$
A : no is multiple of 7 but not divisible by 5 Smallest 5 digit divisible by 7 is 10003 Largest 5 digit divisible by 7 is 99995 $\therefore 99995=10003+( n -1) 7 n =12857$ Numbers divisible by 35 $99995=10010+( P -1) 35 \Rightarrow P =2572$
$\therefore$ Numbers divisible by 7 but not by 35 are $12857-2572=10285$ $\therefore P=\frac{10285}{90000} \therefore 9 P=1.0285$
Ans. (C) [1.0285]
A
$\sqrt{5}-2$
B
$\sqrt{3}-1$
C
$\sqrt{7}-2$
D
$\sqrt{7}-\sqrt{3}$
Solution

$\tan 2 \alpha=\frac{h}{x}$
and $\tan \alpha=\frac{2 h}{x+\sqrt{7} h}$
$\tan \alpha=\frac{2 h}{h \cot 2 \alpha+\sqrt{7} h}$
$\tan \alpha=\frac{2}{\frac{\left(1-\tan ^2 \alpha\right)}{2 \tan \alpha}+\sqrt{7}}$
Put $\tan \alpha=t \&$ simplify
$\Rightarrow \tan \alpha=\sqrt{7}-2$
A
$p$
B
$\sim p$
C
$q$
D
$\sim q$

A
$\frac{1}{11}$
B
$\frac{5}{11}$
C
6
D
7
Solution
Two given planes mutually perpendicular
$ 2(3 k )+ k (- k )+(-5) 1=0$
$k =1,5$
but $k <3 $ So $k =1$
Plane passing through these planes is
$2 x + y -5 z -1+\lambda(3 x - y + z -5)=0$
$\frac{x}{\frac{5 \lambda+1}{2+3 \lambda}}+\frac{y}{\frac{5 \lambda+1}{1-\lambda}}+\frac{z}{\frac{5 \lambda+1}{\lambda-5}}=1$
Given $\frac{5 \lambda+1}{2+3 \lambda}=1 \Rightarrow \lambda=\frac{1}{2}$
So intercept on $y-$ axis $=\frac{5 \lambda+1}{1-\lambda}=7$
A
$\frac{1}{4}$
B
$\frac{3}{4}$
C
$\frac{1}{2}$
D
1
Solution

Given $\Delta_1=\frac{1}{2} \begin{vmatrix}x & y & 1 \\ 1 & 1 & 1 \\ -4 & 3 & 1\end{vmatrix}$
$\& \Delta_2=\frac{1}{2}\begin{vmatrix}1 & 1 & 1 \\ -4 & 3 & 1 \\ -2 & -5 & 1\end{vmatrix}$
Given $\frac{\Delta_1}{\Delta_2}=\frac{4}{7} \Rightarrow \frac{-2 x-5 y+7}{36}=\frac{4}{7}$ $\Rightarrow 14 x+35 y=-95 \ldots .(1)$
Equation of $BC$ is $4 x + y =-13$....(2)
Solve equation (1) \& (2)
Point $P\left(\frac{-20}{7}, \frac{-11}{7}\right)$
Here point $Q\left(\frac{-1}{2}, 0\right) \& R\left(\frac{1}{2}, 0\right)$
So Area of triangle $AQR =\frac{1}{2} \times 1 \times 1=\frac{1}{2}$
A
$\sqrt{11}$
B
4
C
3
D
$2 \sqrt{23}$
Solution
Given circle $x^2+y^2-2 g x+6 y-19 c=0$
Passes through $(6,1)$
$12 g +19 c =43.....$(1)
Centre $( g ,-3)$ lies on given line
So, $g+6 c=8 .....$(2)
Solve equation (1) \& (2)
$c =1 \& g =2$
equation of circle $x^2+y^2-4 x+6 y-19=0$
Length of intercept on $x$-axis
$=2 \sqrt{g^2-c}=2 \sqrt{23}$
A
$f$ is not differentiable at $x =4$
B
$f^{\prime}(3)+f^{\prime}(5)=\frac{35}{4}$
C
$f$ is increasing in $\left(-\infty, \frac{1}{8}\right) \cup(8, \infty)$
D
$f$ has a local minima at $x=\frac{1}{8}$
Solution
Given $f(x) \begin{cases}\int\limits_0^x(5-|t-3|) d t, & x>4 \\ x^2+b x & x \leq 4\end{cases}$
$f ( x )$ is continuous at $x =4$
So $\displaystyle\lim _{x \rightarrow 4^{-}} f(x)=\displaystyle\lim _{x \rightarrow 4^{+}} f(x)=f(4)$
So $16+4 b =\int_0^3(2-t) d t+\int\limits_3^4(8-t) d t$
$\Rightarrow 16+4 b=15$
So $b=\frac{-1}{4}$
At $x=4$
$ LHD =2 x + b =\frac{31}{4} $
$ RHD =5-|x-3|=4$
$ LHD \neq RHD$
Option (A) is true
and $f ^{\prime}(3)+ f ^{\prime}(5)=\frac{23}{4}+3=\frac{35}{4}$
Option (B) is true
$ \because f(x)=x^2-\frac{x}{4} \text { at } x \leq 4 $
$f^{\prime}(x)=2 x-\frac{1}{4}$
This function is not increasing.
In the interval in $x \in\left(-\infty, \frac{1}{8}\right)$
Option (C) is NOT TRUE.
This function $f(x)$ is also local minima at
$x=\frac{1}{8}$
Answer: 12
Solution
$ \cos \left(\sin ^{-1} x\right)=\cos \left(\cos ^{-1} \sqrt{1-x^2}\right)=\sqrt{1-x^2} $
$ \cot \left(\tan ^{-1} \sqrt{1-x^2}\right)=\cot \cot ^{-1}\left(\sqrt{\frac{1}{\sqrt{1-x^2}}}\right)=\frac{1}{\sqrt{1-x^2}} $
$ \Rightarrow \cos \left(\sin ^{-1}\left(\frac{x}{\sqrt{1-x^2}}\right)\right)=\frac{\sqrt{1-2 x^2}}{\sqrt{1-x^2}} $
$ \Rightarrow \frac{\sqrt{1-2 x^2}}{\sqrt{1-x^2}}=k$
$ \Rightarrow 1-2 x^2=k^2\left(1-x^2\right)$
$ \Rightarrow\left(k^2-2\right) x^2=k^2-1$
$ x^2=\frac{k^2-1}{k^2-2} $
$ \alpha=\sqrt{\frac{k^2-1}{k^2-2}} \Rightarrow \alpha^2=\frac{k^2-1}{k^2-2}$
$ \beta=\sqrt{\frac{k^2-1}{k^2-2}} \Rightarrow \beta^2=\frac{k^2-1}{k^2-2}$
$ \frac{1}{\alpha^2}+\frac{1}{\beta^2}=2\left(\frac{k^2-2}{k^2-1}\right) \& \frac{\alpha}{\beta}=-1 $
Sum of roots $=\frac{1}{\alpha^2}+\frac{1}{\beta^2}+\frac{\alpha}{\beta}=b $
$ \Rightarrow \frac{2\left(k^2-2\right)}{k^2-1}-1=b \ldots .(1) $
Product of roots $=\left(\frac{1}{\alpha^2}+\frac{1}{\beta^2}\right) \frac{\alpha}{\beta}=-5$
$ \Rightarrow \frac{2\left(k^2-2\right)}{k^2-1}(-1)=-5 $
$ \Rightarrow 2 k^2-4=5 k^2-5$
$ \Rightarrow 3 k^2=1 \Rightarrow k^2=\frac{1}{3} \ldots . \text { Put in (1) }$
$ \Rightarrow b=\frac{2\left(k^2-2\right)}{k^2-1}-1=5-1=4 $
$ \frac{b}{k^2}=\frac{4}{\frac{1}{3}}=12$
Answer: 2
Solution
$ n =10, \bar{x}=\frac{\sum x_i}{10}=15 $
$6^2=\frac{\sum x_i^2}{10}-(\bar{x})^2=15 $
$ \Rightarrow \displaystyle\sum_{i=1}^{10} x_i=150$
$ \Rightarrow \displaystyle\sum_{i=1}^9 x_i+25=150 $
$ \Rightarrow \displaystyle\sum_{i=1}^9 x_i=125 $
$ \Rightarrow \displaystyle\sum_{i=1}^9 x_i+15=140$
Actual mean $=\frac{140}{10}=14=\bar{x}_{\text {new }} $
$\displaystyle\sum_{i=1}^9 \frac{x_i^2+25^2-15^2}{10}=15$
$ \Rightarrow \displaystyle\sum_{i=1}^9 x_i^2+625=2400$
$ \displaystyle\sum_{i=1}^9 x_i^2=1775 $
$\displaystyle \sum_{i=1}^9 x_i^2+15^2=2000=\left(\sum x_i^2\right)_{\text {actual }} $
$ 6_{\text {actual }}^2=\frac{\left(\sum x_i^2\right)_{\text {actual }}-\left(\bar{x}_{\text {new }}\right)^2}{10} $
$ =\frac{2000}{10}-14^2$
$ =200-196=4 $
(S.D) actual $=6=2$
Answer: 12
Solution
Equation of plane
$ 4 a x-y+5 z-7 a+\lambda(2 x-5 y-z-3)=0$
this satisfy $(4,-1,0) $
$16 a+1-7 a+\lambda(8+5-3)=0 $
$9 a+1+10 \lambda=0......$(1)
Normal vector of the plane $A$ is $(4 a+2 \lambda,-1-5 \lambda, 5-\lambda)$ vector along the line which contained the plane $A$ is
$ i -2 j + k $
$\therefore 4 a+2 \lambda+2+10 \lambda+5-\lambda=0$
$ 11 \lambda+4 a+7=0 \ldots . (2) $
Solve (1) and (2) to get $a =1, \lambda=-1$
Now equation of plane
$x+2 y+3 z-2=0$
Let the point in the line $\frac{x-3}{7}=\frac{y-2}{-1}=\frac{z-3}{-4}=t$
is $(7 t+3,-t+2,-4 t+3)$ satisfy the equation of plane $A$
$ 7 t +3-2 t +4+9-12 t -2=0 $
$ t =2$
So $\alpha+\beta+\gamma=2 t+8=12$
Answer: 1552
Solution
Hyp : $\frac{y^2}{64}-\frac{x^2}{49}=1$
An ellipse $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ passes through the vertices of the hyperbola $H: \frac{x^2}{49}-\frac{y^2}{64}=-1$
So $b^2=64$
$e_H=\sqrt{1+\frac{a^2}{b^2}}=\sqrt{1+\frac{49}{64}}$
Ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
$ e_E=\sqrt{1-\frac{a^2}{b^2}}=\sqrt{1-\frac{a^2}{64}}$
$b=8, \sqrt{\frac{1-a^2}{64}} \times \frac{\sqrt{113}}{8}=\frac{1}{2} \Rightarrow \sqrt{64-a^2} \times \sqrt{113}=32$
$ \left(64-a^2\right)=\frac{32^2}{113} $
$ \Rightarrow a^2=64-\frac{32^2}{113} $
$ l=\frac{2 a^2}{b}=\frac{2}{8}\left(64-\frac{32^2}{113}\right)=\frac{1552}{113} $
$113 l=1552$
Answer: 1
Solution
$ \sin \left(2 x^2\right) \ln \left(\tan x^2\right) d y+\left(4 x y-4 \sqrt{2} x \sin \left(x^2-\frac{\pi}{4}\right)\right) d x=0$
$ \ln \left(\tan x^2\right) d y+\frac{4 x y d x}{\sin \left(2 x^2\right)}-\frac{4 \sqrt{2} x \sin \left(x^2-\frac{\pi}{4}\right)}{\sin \left(2 x^2\right)} d x=0$
$d\left(y \cdot \ln \left(\tan x^2\right)\right)-4 \sqrt{2} x \frac{\left(\sin x^2-\cos x^2\right)}{\sqrt{2}-2 \sin x^2 \cos x^2} d x=0$
$ d\left(y \ln \left(\tan x^2\right)\right)-\frac{4 x\left(\sin x^2-\cos x^2\right)}{\left(\sin x^2+\cos ^2\right)-1} d x=0 $
$ \Rightarrow \int d\left(y \ln \left(\tan x^2\right)\right)+2 \int \frac{d t}{t^2-1}=\int 0$
$ \Rightarrow y \ln \left(\tan x^2\right)+2 \cdot \frac{1}{2} \ln \left|\frac{t-1}{t+1}\right|=c$
$y \ln \left(\tan x^2\right)+\ln \left(\frac{\sin x^2+\cos x^2-1}{\sin x^2+\cos x^2+1}\right)=c$
Put $y =1$ and $x=\sqrt{\frac{\pi}{6}}$
$1 \ln \left(\frac{1}{\sqrt{3}}\right)+\ln \frac{\left(\frac{1}{2}+\frac{\sqrt{3}}{2}-1\right)}{\left(\frac{1}{2}+\frac{\sqrt{3}}{2}+1\right)}=c$
Now
$x=\sqrt{\frac{\pi}{3}} \Rightarrow y(\ln \sqrt{3})+\ln \frac{\left(\frac{1}{2}+\frac{\sqrt{3}}{2}-1\right)}{\left(\frac{1}{2}+\frac{\sqrt{3}}{2}+1\right)}=\ln \left(\frac{1}{\sqrt{3}}\right)+\ln \left(\frac{\sqrt{3}-1}{\sqrt{3}+3}\right)$
$y(\ln \sqrt{3})=\ln \left(\frac{1}{\sqrt{3}}\right) $
$\Rightarrow y =-1$
$ |y|=1$
Answer: 2
Solution
$y^5-9 xy +2 x =0 $
$ 5 y^4 \frac{d y}{x}-9 x \frac{d y}{d x}-9 y+2=0$
$ \frac{d y}{d x}\left(5 y^4-9 x\right)=9 y-2$
$ \frac{d y}{d x}=\frac{9 y-2}{5 y^4-9 x}=0 $ (for horizontal tangent) $y=\frac{2}{9} \Rightarrow $ Which does not satisfy the original equation $\Rightarrow M =0$
Now $5 y ^4-9 x =0 $ (for vertical tangent)
$ 5 y ^4(9 y -2)-9 y ^5=0$
$ y ^4[45 y -10-9 y ]=0 $
$ y =0 (Or) 36 y =10 $
$ y=\frac{5}{18}$
$ y=0 \Rightarrow x=0 \& y=\frac{5}{18} \Rightarrow x= $
$(0,0) \left(x, \frac{5}{18}\right)$
$N =2$
$ M + N =0+2=2$
Answer: 10620
Solution
$ f ( x )=2 x ^2- x -1 $
$ | f ( x )| \leq 800 $
$ 2 n ^2- n -801 \leq 0$
$ n^2-\frac{1}{2} n-\frac{801}{2} \leq 0$
$ \left(n-\frac{1}{4}\right)^2-\frac{801}{2}-\frac{1}{16} \leq 0$
$ \left(n-\frac{1}{4}\right)^2-\frac{6409}{16} \leq 0 $
$ \left(n-\frac{1}{4}-\frac{\sqrt{6409}}{4}\right)\left(n-\frac{1}{4}+\frac{\sqrt{6409}}{16}\right) \leq 0 $
$\frac{1-\sqrt{6409}}{4} \leq n \leq \frac{1+\sqrt{6409}}{4} $
$ n=\{-19,-18-17, \ldots \ldots . .0,1,2, \ldots \ldots, 20\}$
$\displaystyle \sum_{n \in S} f(x)=\sum\left(2 x^2-x-1\right) $
$ =2\left[19^2+18^2+\ldots . .+1^2+1^2+2^2+\ldots .+19^2+20^2\right]$
$ =4\left[1^2+2^2+\ldots .+19^2\right]+2\left[20^2\right]-20-40$
$ =\frac{4 \times 19 \times 20 \times(2 \times 19+1)}{6}+2 \times 400-60$
$ =\frac{4 \times 19 \times 20 \times 39}{6}+800-60-9880+800-60 $
$=10620$
Answer: 5376
Solution
$ \operatorname{Tr}\left(A A^T\right)=6$
$ AA ^{ T }= \begin{bmatrix}a & d & g \\b & e & h \\c & f & i\end{bmatrix}\begin{bmatrix} a & b & c \\d & e & f \\g & h & i\end{bmatrix}$
Now give
$ a^2+d^2+g^2+b^2+e^2+h^2+c^2+f^2+i^2=6 $
$ ={ }^9 C_3 \times 2^6$
$ =5376$
Answer: 75
Solution
$\lambda+\ell=75 $
$ x^2+4 y^2+2 x+8 y-\lambda=0$
$ \frac{(x+1)^2}{\lambda+5}+\frac{(y+1)^2}{\frac{\lambda+5}{4}}=1 $
$\because \frac{2 b^2}{a}=4$
$ \frac{2(\lambda+5)}{4}=4(\sqrt{\lambda+5}) $
$ \Rightarrow \lambda=59 $
$\lambda \neq-5$
$ l=2 a=2 \sqrt{\lambda+5}=2 \sqrt{65}=16$
$ \Rightarrow \lambda+\ell=59+16=75$
Answer: 0




















