JEE Main Physics Question Paper with Solution 2023 June 27th Shift 2 - Evening
A
$\left[ ML ^{-1} T ^{-1}\right]$
B
$\left[ ML ^{-1} T ^{-2}\right]$
C
$\left[ ML ^{2} T ^{-1}\right]$
D
$\left[ M ^{-1} L ^{3} T ^{0}\right]$
Solution
Pascal second
$\frac{ F }{ A } t =\frac{ MLT ^{-2}}{ L ^{2}} T = ML ^{-1} T ^{-1}$
A
$2.45 \times 10^{10}\, m$
B
$1.45 \times 10^{10}\, m$
C
$1.45 \times 10^{9} \,m$
D
$0.14 \times 10^{9} \,m$
Solution

$\frac{2000}{60 \times 60} \times \frac{\pi}{180}=\frac{ d }{1.5 \times 10^{\prime \prime}}$
$\Rightarrow d =\frac{2000}{60 \times 60} \times \frac{\pi}{180} \times 1.5 \times 10^{\prime \prime}$
$=\frac{\pi \times 1.5}{3 \times 6 \times 18} \times 10^{\prime \prime}=1.45 \times 10^{9}$
A
$19.6 \, m$
B
$29.4 \, m$
C
$39.2 \, m$
D
$73.5 \, m$
Solution
$ V ^{2}=2 \times 9.8 \times 4.9 $
$ V =9.8\, m / s$
Depth $=$ distance travelled in $3$ seconds
$=9.8 \times 3=29.4\, m$
A
$\frac{ k - m \omega^{2} l_{0}}{ m \omega^{2}}$
B
$\frac{ m \omega^{2} l_{0}}{ k + m \omega^{2}}$
C
$\frac{ m \omega^{2} l_{0}}{ k - m \omega^{2}}$
D
$\frac{ k + m \omega^{2} l_{0}}{ m \omega^{2}}$
Solution

$K \Delta x = m \left(\ell_{0}+\underline{\underline{\Delta}} x \right) w ^{2}$
$K \Delta x = m \ell_{0} w ^{2}+ mw ^{2} \Delta x$
$\Delta x =\frac{ m \ell_{0} w ^{2}}{ k - mw ^{2}}$
A
3
B
2
C
1
D
5
Solution
$v=\sqrt{u^{2}-2 g L}$
$\Delta v=\sqrt{u^{2}+v^{2}}$
$\Delta v=\sqrt{u^{2}+v^{2}-2 g L}$
$\Delta v=\sqrt{2 u^{2}-2 g L}$
$\Delta v=\sqrt{2\left(u^{2}-g L\right)} x=2$
A
$-\frac{ Gm }{ d }[(4+\sqrt{2}) m +4 \sqrt{2} M ]$
B
$-\frac{ Gm }{ d }[(4+\sqrt{2}) M +4 \sqrt{2} m ]$
C
$-\frac{ Gm }{ d }\left[3 m ^{2}+4 \sqrt{2} M \right]$
D
$-\frac{ Gm }{ d }\left[6 m ^{2}+4 \sqrt{2} M \right]$
Solution

$-\frac{ Gm ^{2}}{ d } \times 4-\frac{ Gm ^{2}}{\sqrt{2} d } \times 2-\frac{ GMm }{ d } \times 4 \sqrt{2}$
$-\frac{ Gm }{ d }[(4+\sqrt{2}) m +4 \sqrt{2} M ]$
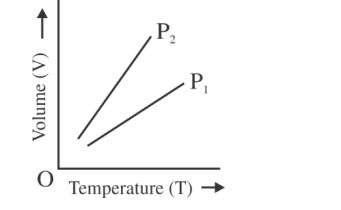
A
$P _{1} > P _{2}$
B
$P _{1}< P _{2}$
C
$P _{1}= P _{2}$
D
Insufficient data to draw any conclusion
Solution
$PV = nRT$
$\frac{ V }{ T }=\frac{ nR }{ P }$
$\frac{ nR }{ P _{1}}<\frac{ nR }{ P _{2}}$
$P _{2}< P _{1}$
A
A and C only
B
B and C only
C
A and B only
D
C and D only
Solution
$\lambda=\frac{ kT }{\sqrt{2} \pi d ^{2} P }$
A
$125\, ms ^{-1}$
B
$500 \,ms ^{-1}$
C
$250 \,ms ^{-1}$
D
$600 \,ms ^{-1}$
Solution
$m \times 125 \times 200+ m \times 2.5 \times 10^{4}=\frac{1}{2} mv ^{2} \times \frac{40}{100}$
$V =500 \,m / s$
A
$0 \,cm \,s ^{-1}$
B
$157 \, cm \, s ^{-1}$
C
$272 \,cm \, s ^{-1}$
D
$314 \, cm \,s ^{-1}$
Solution
$x =\sin \pi\left( t +\frac{1}{3}\right)$
$x =\sin \left(\pi t +\frac{\pi}{3}\right)$
$V =\frac{ dx }{ dt }=\cos \left(\pi t +\frac{\pi}{3}\right) \pi$
$=-\pi \times \frac{1}{2}=157\, cm / s$
A
$\frac{ q }{\varepsilon_{0}}$
B
$\frac{ q }{2 \varepsilon_{0}}$
C
$\frac{q}{4 \varepsilon_{0}}$
D
$\frac{q}{2 \pi \varepsilon_{0}}$
Solution

Total flux through complete spherical surface is $\frac{ q }{\varepsilon_{0}}$
So the flux through curved surface will be $\frac{ q }{2 \varepsilon_{0}}$. The flux through flat surface will be zero.
Remark : Electric flux through flat surface is zero but no option is given, option is available for electric flux passing through curved surface.
A
$1: 1$
B
$1: 4$
C
$\sqrt{3}: 2$
D
$\sqrt{3}: 1$
Solution

$F =\frac{ k (2)(2)}{(1)^{2}}$
$( F =$ Force between two charges $)$.
$F =4 k$
$F _{\text {net }}=2 F \cos 30^{\circ}=2 \cdot F \cdot \frac{\sqrt{3}}{2}= F \sqrt{3}$
$\left( F _{\text {net }}=\right.$ Net electrostatic force on one charged ball $)$
$\frac{ F _{\text {net }}}{ F }=\frac{\sqrt{3} F }{ F }=(\sqrt{3})$
Remark: Net force on any one of the ball is zero. But no option given in options.
A
2
B
1
C
3
D
-3
Solution

$B _{\text {net }}= B _{1}- B _{2}=\frac{\mu_{0} \times 4}{2 \pi[.04]}-\frac{\mu_{0} \times 2}{2 \pi[.06]}$
$\vec{ B }_{\text {net }}=\frac{\mu_{0}}{2 \pi}\left[\frac{200}{3}\right](-\hat{ k })$
$\vec{ F }= q [\vec{ v } \times \vec{ B }]$
$=[3 \pi]\left[(2 \hat{ i }+3 \hat{ j }) \times\left(\frac{\mu_{0}}{2 \pi}\right)\left(\frac{200}{3}\right)-\hat{ k }\right]$
$=3 \pi \times \frac{\mu_{0}}{2 \pi}\left(\frac{200}{3}\right)[2 \times \hat{ j }-3(\hat{ i })]$
$=\left(4 \pi \times 10^{-7}\right)(100)(-3 \hat{ i }+2 \hat{ j })$
$=4 \pi \times 10^{-5} \times[-3 \hat{ i }+2 \hat{ j }]$
A
$RC$
B
$\frac{L}{R}$
C
$\sqrt{ LC }$
D
$\frac{ L }{ C }$
Solution
$\left(\frac{L}{C}\right)$ does not have dimension of time. $RC , \frac{ L }{ R }$ are time constant while $\sqrt{ LC }$ is reciprocal of angular frequency or having dimension of time.
A
Both statement I and statement II are true.
B
Both statement I and statement II are false.
C
Statement I is correct but statement II is false.
D
Statement I is incorrect but statement II is true.
Solution
The statement II is wrong as the velocity of $\varepsilon m$ wave in a medium is $\frac{1}{\sqrt{\mu \varepsilon}}=\frac{1}{\sqrt{\mu_{0} \mu_{ r } \varepsilon_{0} \varepsilon_{ r }}}$.
A
Power of $L _{1}=\frac{ P }{2}$
B
Power of $L _{2}=\frac{ P }{2}$
C
Power of $L _{3}=\frac{ P }{2}$
D
Power of $L _{1}= P$

A
wavelength speed and frequency decreases.
B
wavelength increases, speed decreases and frequency remains constant.
C
wavelength and speed decreases but frequency remains constant.
D
wavelength, speed and frequency increases.

A
Both statement I and statement II are true.
B
Both statement I and statement II are false
C
Statement I is correct but statement II is false
D
Statement I is incorrect but statement II is true.
Solution
When electron jump from lower to higher energy level, energy absorbed so statement-I incorrect. When electron jump from higher to lower energy level, energy of emitted photon
$E = E _{2}- E _{1}$
$hf = E _{2}- E _{1}$
$ \Rightarrow f =\frac{ E _{2}- E _{1}}{ h }$
so statement-II is correct.
A
Active region
B
Saturation state only
C
Cut-off state only
D
Saturation and cut-off state
Solution
Transistor act as a switch in saturation and cut of region
A
All statements are true
B
(a), (b) and (c) are true only
C
(a), (c) and (d) are true only
D
(b), (c) and (d) are true only
Solution
(a) For low frequency or high wavelength size of antenna required is high.
(b) E P R is low for longer wavelength.
(c) yes we want to avoid mixing up signals transmitted by different transmitter simultaneously.
(d) Low frequency signals sent to long distance by superimposing with high frequency.
Answer: 3
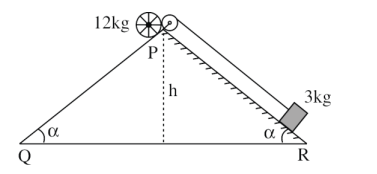
Solution

$T \sin \theta=30$
$T \cos \theta=100$
$\Rightarrow \tan \theta=0.3$
Answer: 3
Solution
Net loss in $PE =$ Gain in $KE$
$12 gh -3 gh =\frac{1}{2} 3 v ^{2}+\frac{1}{2} 12 v ^{2}+\frac{1}{2}\left[12 r ^{2}\right]\left(\frac{ v }{ r }\right)^{2}$
$9 gh =\frac{1}{2}[3+12+12] v ^{2}$
$v^{2}=\frac{2 g h}{3} \Rightarrow v=\frac{1}{2} \sqrt{\frac{8}{3} g h}$
$x=\frac{8}{3} \simeq 3$
Answer: 1400
Solution
$Q = nC _{ p } \Delta T =\frac{ nv }{ v -1} R \Delta T$
$Q =\frac{ v }{ v -1} \omega=\frac{1.4}{0.4} \times 400=1400\, J$
Answer: 1
Solution
$t =\frac{\Delta \phi}{\omega}=\frac{\pi / 2-\pi / 6}{2 \pi / 6}=\frac{\pi / 3}{\pi / 3}=1 \,\sec$
Answer: 23
Solution
Parallel combination
$c _{ eq }=\varepsilon_{0} A \left[\frac{1}{5 b }+\frac{1}{3 b }+\frac{1}{ b }\right]=\frac{23}{15} \frac{\varepsilon_{0} A }{ b }$
Answer: 12
Solution

$I=\int JdA$
$=\int 10^{6} \times 2 \pi xdx$
$\left.=10^{6} \times 2 \pi \cdot x \frac{ x ^{2}}{2}\right]_{\frac{ r }{2}}^{ r }$
$=\pi \times 10^{6}\left[ r ^{2}-\frac{ r ^{2}}{4}\right]=12 \pi$
$x =12$
Answer: 3
Solution
$R =\left(\frac{ ma }{3}\right)+\left(\frac{ a }{2 m }\right)$
$\frac{ dR }{ dm }=\frac{ a }{3}-\frac{ a }{2 m ^{2}}=0$
$\frac{ a }{3}=\frac{ a }{2 m ^{2}}$
$m ^{2}=\frac{3}{2}$
$m =\sqrt{\frac{3}{2}}$
$x =3$
Answer: 2
Solution

$R =\frac{ mv }{ q _{ B }}$
$R _{ D }=\frac{\left(2 m _{ P }\right) v _{ D }}{ eB }$
$R _{ P }=\frac{\left( m _{ P }\right) v _{ P }}{ e B }$
$\frac{ R _{ D }}{ R _{ P }}=\frac{2 v _{ D }}{ v _{ P }}=\frac{2 v _{ D }}{\sqrt{2} v _{ D }}=\frac{\sqrt{2}}{1}$
$\frac{1}{2}(2 mp ) v _{ D }^{2}=\frac{1}{2} m _{ P } \cdot v _{ P }^{2}$
$\sqrt{2} v _{ D }= v _{ P }$
$x =2$
Answer: 16
Solution
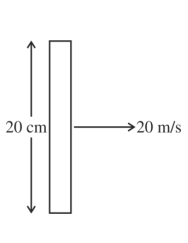
$B _{ H }=4 \times 10^{-3} T$
$\theta \rightarrow 45^{\circ}$
$B _{ V }= B _{ H }$
$\epsilon=(\overrightarrow{ V } \times \overrightarrow{ B }) \cdot \vec{\ell}$
$=\left(\left(4 \times 10^{-3}\right)(20)\right) \frac{20}{100}$
$=16 \times 10^{-3} V =16\, mV$
Answer: 4
Solution

$1- I (60)-0.6- I (40)=0$
$\frac{0.4}{100}= I$
$I =4\, mA$
JEE Main Chemistry Question Paper with Solution 2023 June 27th Shift 2 - Evening
A

B

C

D

Solution
$P\, vs \,d:$
$P =\left(\frac{ RT }{ M }\right) d$

A
In this molecule, orbitals of phosphorous are assumed to undergo $sp ^{3} d$ hybridization.
B
The geometry of $PCl _{5}$ is trigonal bipyramidal.
C
$PCl _{5}$ has two axial bonds stronger than three equatorial bonds.
D
The three equatorial bonds of $PCl _{5}$ lie in a plane.
Solution
In $PCl _{5}$, axial bonds are weaker than equatorial.
A
Both Statement I and Statement II are correct
B
Both Statement I and Statement II are incorrect
C
Statement I is correct but Statement II is incorrect
D
Statement I is incorrect but Statement II is correct
Solution
Statement-1 : wrong, $Au ^{+}$is correct, not $Au ^{+3}$
Statement-2 : correct
A
$HCN < H _{2} O < NH _{3}$
B
$HCN < CH _{4}< NH _{3}$
C
$CH _{4}< HCN < NH _{3}$
D
$CH _{4}< NH _{3}< HCN$
Solution
Order of H-Bonding
$CH _{4}< HCN < NH _{3}$
$NCH \ldots . NCH$
$H _{2} NH \ldots NH _{3}$
A
$Mg ^{2+}< Na ^{+}< F ^{-}< O ^{2-}< N ^{3-}$
B
$N ^{3-}< O ^{2-}< F ^{-}< Na ^{+}< Mg ^{2+}$
C
$F ^{-}< Na ^{+}< O ^{2-}< Mg ^{2+}< N ^{3-}$
D
$Na ^{+}< F ^{-}< Mg ^{2+}< O ^{2-}< N ^{3-}$
Solution
$N ^{-3}> O ^{-2}> F ^{-}> Na ^{+}> Mg ^{+2}$ (Radii) (Isoelectronic species)
A
$NH _{3}$
B
$N _{2}$
C
$N _{2} O$
D
$Cl _{2}$

A
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$.
B
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$.
C
$A$ is correct but $R$ is not correct.
D
$A$ is not correct but $R$ is correct
Solution
Both A and R are correct and R is the correct explanation of A.
A
$Cr$
B
$Fe$
C
$Cu$
D
$Zn$
Solution
$ Cr ^{+2} / Cr \rightarrow-0.90 \,V $
$ Fe ^{+2} / Fe \rightarrow-0.44 \,V $
$Cu ^{+2} / Cu \rightarrow+0.34 \,V $
$ Zn ^{+2} / Zn \rightarrow-0.76 \,V$
So Ans. $Cu ^{+2} / Cu$
A
$Eu ^{2+}$ and $Tm ^{2+}$
B
$Sm ^{2+}$ and $Tm ^{3+}$
C
$Tb ^{4+}$ and $Yb ^{2+}$
D
$Dy ^{3+}$ and $Yb ^{3+}$
Solution
$Tb \rightarrow 4 f ^{9} 6 s ^{2}$
$Tb ^{+4} \rightarrow 4 f ^{7}$
$Yb \rightarrow 4 f ^{14} 6 s ^{2}$
$Yb ^{+2} \rightarrow 4 f ^{14}$
A
A < B < D < C
B
B < D < C < A
C
A < C < D < B
D
B < D < A < C
Solution
A
$HOCl , HNO _{3}, Cl _{2}$
B
$Cl _{2}, HNO _{3}, HOCl$
C
$HClO _{2}, HNO _{2}, HOCl$
D
$HOCl , HNO _{2}, Cl _{2} O$

A
A-IV, B-III, C-II, D-I
B
A-IV, B-III, C-I, D-II
C
A-II, B-III, C-I, D-IV
D
A-IV, B-II, C-III, D-I
Solution
A
$63^{\circ} C$
B
$90^{\circ} C$
C
$104^{\circ} C$
D
$142^{\circ} C$

A
It is a linear polymer of 1, 3-butadiene.
B
It is obtained by copolymerization of 1,3butadiene and styrene.
C
It is obtained by copolymerization of 1,3butadiene and acrylonitrile.
D
The suffix N in Buna-N stands for its natural occurrence
Solution
It is copolymerization of 1, 3-butadiene and acrylonitrile.
A
Both Statement I and Statement II are true
B
Both Statement I and Statement II are false
C
Statement I is true but Statement II is false
D
Statement I is false but Statement II is true

A
A-III, B-I, C-II, D-IV
B
A-III, B-I, C-IV, D-II
C
A-I, B-IV, C-II, D-III
D
A-I, B-III, C-II, D-IV
Solution
A. Antipyretic - Reduces fever
B. Analgesic - Reduces pain
C. Tranquilizer - Reduces stress
D. Antacid - Reduces acidity (Stomach)
A
A-III, B-I, C-II, D-IV
B
A-II, B-I, C-IV, D-III
C
A-IV, B-I, C-III, D-II
D
A-IV, B-I, C-II, D-III
Solution
$CO _{3}{ }^{2-}$ will give $CO _{2}( g )$ which will turns lime water milky.
$S ^{2-}$ will give $H _{2} S ( g )$, will turns lead acetate paper
black
$SO _{3}{ }^{2-}$ will give $SO _{2}( g )$, which will turns acidified potassium dichromate solution green.
$NO _{2}{ }^{-}$will give brown $NO _{2}( g )$ will turn $KI$ solution blue.
Answer: 2
Solution
$\% H =\frac{7.5}{116} \times 100=6.5$
$\% O =\frac{60}{116} \times 100=51.7$
$\% C =\frac{48.5}{116} \times 100=41.8$
Relative atomicities $= H \Rightarrow 6.5$
$O \Rightarrow \frac{51.7}{16}=3.25$
$C \Rightarrow \frac{41.8}{12}=3.5$
Emperically formula is approx.. $CH _{2} O$
(A) $C _{2} H _{4} O _{2}$ (B) $CH _{2} O$ relate to this formula.
Answer: 2
Solution
Quantum no. of $\operatorname{set}(B)$ and $(C)$ can be correct. (A) and (D) are wrong as $n=\ell$ is not possible.
Answer: 8630
Solution
$n =5 \,mol$
$T =300 \,K$
$V _{1}=10 \,L$
$V _{2}=20\, L$
$w =- nRT \ell n \frac{ V _{2}}{ V _{1}}$
$=-5 \times 8.3 \times 300 \times \ell n \frac{20}{10}$
$=-8630.38 \, J$
Answer: 45
Solution
$W =2.5\, g $
$ K _{ b }=0.52 $
$ W _{\text {solvent }}=75 g $
$ M =$ Mol. Wt. of solute
$ T _{ B }^{\prime}=373.535 \,K $
$ T _{ B }^{ o }=373.15\, K$
$ \Delta T _{ B }=0.385= K _{ b } $ molality
$ 0.385=0.52 \times\left(\frac{2.5}{ M } \times \frac{1000}{75}\right) $
$M =45\, g \,mol ^{-1}$
Answer: 11
Solution
$0.001 M NaOH$
${\left[ OH ^{-}\right]=10^{-3} }$
$pOH =3$
$pH =11$
Answer: 51
Solution
$\frac{1}{2} H _{2}+ Ag ^{+} \rightarrow H ^{+}+ Ag$
$\Delta G ^{\circ}=- nE ^{\circ} F$
$=-1 \times 0.5332 \times 96500\, J$
$=-51.35\, kJ$
$\left( n =2\right.$ for $\left.H _{2}+2 Ag ^{+} \rightarrow 2 H ^{+}+2 Ag \right)$
Answer: 59
Solution
$\log _{10} \frac{ K _{2}}{ K _{1}}=\frac{ E _{ a }}{2.303 R }\left(\frac{1}{300}-\frac{1}{309}\right)$
$0.3=\frac{ E _{ a }}{2.303 \times 8.3}\left(\frac{9}{300 \times 309}\right)$
$E _{ a }=\frac{0.3 \times 2.303 \times 8.3 \times 300 \times 309}{9}$
$=59065.04\, J$
$E _{ a }=59.06 \,kJ$
Answer: 12
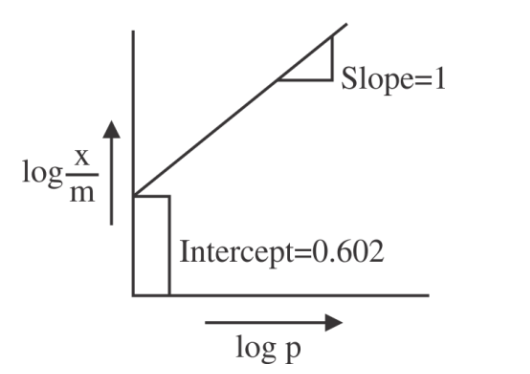
Solution
$\frac{x}{ m }= kP ^{\frac{1}{ n }} $
$\log \frac{ x }{ m }=\log k +\frac{1}{ n } \log P$
From graph
Slope $=\frac{1}{n}=1 \Rightarrow n=1$
Intercept $=\log k =0.602$
$k =4$
$\frac{x}{ m }=4 \times(0.03)^{\frac{1}{1}}$
$\frac{ x }{ m }=12 \times 10^{-2}$
Answer: 40
Solution
wt. of organic compound $=0.25\, g$
mass of $Cl =\frac{35.5}{143.5} \times 0.4 \,g$
mass $\%$ of $Cl$ in the organic compound
$=\frac{35.5 \times 0.4}{143.5 \times 0.25} \times 100 $
$=39.58 \%$
JEE Main Mathematics Question Paper with Solution 2023 June 27th Shift 2 - Evening
A
0
B
1
C
2
D
3
Solution
$C:(x-4)^{2}+(y-3)^{2}=4$
$E: \frac{(x-2)^{2}}{9}+\frac{y^{2}}{5}=1$

Lower Extremity of vertical diameter of circle $\rightarrow(4,1)$
Put in ellipse $\Rightarrow \frac{(4-2)^{2}}{9}+\frac{1}{5}-1$
$=\frac{4}{9}+\frac{1}{5}-1$
$=\frac{29}{45}-1 < 0$
Two Solution
A
117
B
106
C
125
D
136
Solution
$f(x)=\begin{vmatrix}a & -1 & 0 \\ a x & a & -1 \\ a^{2} & a x & a\end{vmatrix}$
$f(x)=a \begin{vmatrix}1 & -1 & 0 \\ x & a & -1 \\ x^{2} & a x & a\end{vmatrix}$
$=a\left[1\left(a^{2}+a x\right)+1\left(a x+x^{2}\right)\right]$
$\Rightarrow f(x)=a(x+a)^{2}$
so, $f^{\prime}(x)=2 a(x+a)$
as, $2 f^{\prime}(10)-f^{\prime}(5)+100=0$
$\Rightarrow 2 \times 2 a(10+a)-2 a(5+a)+100=0$
$\Rightarrow 40 a+4 a^{2}-10 a-2 a^{2}+100=0$
$2 a ^{2}+30 a +100=0$
$\Rightarrow a ^{2}+15 a +50=0$
$( a +10)( a +5)=0$
$a =-10$ or $a =-5$
Required $=(-10)^{2}+(-5)^{2}=125$
A
$-2+\sqrt{3}$
B
$2-\sqrt{3}$
C
$2+\sqrt{3}$
D
$-2-\sqrt{3}$
Solution
$a =\alpha- i \beta ; \alpha \in R ; \beta \in R$
$4 ix +(1+ i ) y =0$ and
$8\left(\cos \frac{2 \pi}{3}+ i \sin \frac{2 \pi}{3}\right) x +\overline{ a y}=0$
$\left|\begin{array}{cc}4 i & 1+ i \\ 8 e ^{ i 2 \pi / 3} \overline{ a }\end{array}\right|=0$
$\Rightarrow 4 i \overline{ a }-(1+ i ) 8 e ^{ i 2 \pi / 3}=0$
$\Rightarrow 4 i (\alpha+ i \beta)-8(1+ i )\left(\frac{-1+ i \sqrt{3}}{2}\right)=0$
$\Rightarrow i \alpha-\beta+1+\sqrt{3}+ i (1-\sqrt{3})=0$
$\Rightarrow \beta=\sqrt{3}+1$
$\alpha=\sqrt{3}-1$
So, $\frac{\alpha}{\beta}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}$
A
16
B
32
C
64
D
128
Solution
$AB = i$
$|\text{adj}\left( B\right.$ adj $(2 A )|=| B$ adj $\left.(2 A )\right|^{2}$
$=| B |^{2}$ |adj $\left.(2 A )\right|^{2}$
$=| B |^{2}\left(|2 A |^{2}\right)^{2}=| B |^{2}\left(2^{6}| A |^{2}\right)^{2}$
$| A |=\frac{1}{8}$ and $| AB |=1 \Rightarrow| A || B |=1$
$\Rightarrow \frac{1}{8}| B |=1$
$\Rightarrow| B |=8$
required value $=64$
A
$\left(\frac{7}{3}\right)^{2}$
B
$\frac{7^{3}}{3^{2}}$
C
$\left(\frac{7}{3}\right)^{3}$
D
$\frac{7^{2}}{3^{3}}$
Solution

$\Rightarrow \frac{6^{2} S }{7^{2}}=\frac{2}{1-\frac{1}{7}}=\frac{2}{6} \times 7$
$\Rightarrow S -\frac{2 \times 7^{3}}{6^{3}} \Rightarrow 4 S -\frac{7^{3}}{3^{3}}-\left(\frac{7}{3}\right)^{3}$
A
$\frac{35}{27}$
B
$1$
C
$\frac{27}{28}$
D
$\frac{28}{27}$
Solution
$a _{1}, a _{2}, a _{3} \ldots . A . P . ; a _{1}=2 ; a _{10}=3 ; d _{1}=\frac{1}{9}$
$b _{1}, b _{2}, b _{3}, \ldots$ A.P. $; b _{1}=\frac{1}{2} ; b _{10}=\frac{1}{3} ; d _{2}=\frac{-1}{54}$
[Using $a _{1} b _{1}=1= a _{10} b _{10} ; d _{1}\, \&\, d _{2}$ are common differences respectively]
$a _{4} \cdot b _{4} =\left(2+3 d _{1}\right)\left(\frac{1}{2}+3 d _{2}\right)$
$=\left(2+\frac{1}{3}\right)\left(\frac{1}{2}-\frac{1}{18}\right)$
$=\left(\frac{7}{3}\right)\left(\frac{8}{18}\right)=\frac{28}{27}$
A
$(3,2)$
B
$(2,3)$
C
$(2,2)$
D
$(3,4)$
Solution
$m=L \cdot \max$
$N=L \cdot \min$
$f(x)=\int\limits_{0}^{x^{2}} \frac{t^{2}-5 t+4}{2+e^{t}} d t$
$f^{\prime}(x)=\frac{\left(x^{4}-5 x^{2}+4\right) 2 x}{2+e^{x^{2}}}=\frac{2 x\left(x^{2}-1\right)\left(x^{2}-4\right)}{2+e^{x^{2}}}$
$=\frac{2 x(x-1)(x+1)(x-2)(x+2)}{2+e^{x^{2}}}$

A
$6-9 \sqrt{2}$
B
$6-\frac{9}{\sqrt{2}}$
C
$\frac{9}{2}-6 \sqrt{2}$
D
$\frac{9}{\sqrt{2}}-6$
Solution
At right hand vicinity of $x =0$ given equation does not satisfy
$\because \text { LHS }=\int\limits_{1^{-}}^{1} t ^{2} f ( t ) dt =0, \text { RHS }=\displaystyle\lim _{ x \rightarrow 0^{+}}\left(\sin ^{3} x +\cos x \right)=1$
LHS $\neq$ RHS hence data given in question is wrong hence BONUS
Correct data should have been
$\int\limits_{\cos x}^{1} t^{2} f(t) d t=\sin ^{3} x+\cos x-1$
Calculation for option
differentiating both sides
$-\cos ^{2} x f(\cos x) \cdot(-\sin x)=3 \sin ^{2} x \cdot \cos x-\sin x$
$\Rightarrow f(\cos x)=3 \tan x-\sec ^{2} x$
$\Rightarrow f^{\prime}(\cos x)(-\sin x)=3 \sec ^{2} x-2 \sec ^{2} x \tan x$
$\Rightarrow f^{\prime}(\cos x) \cos x=\frac{2}{\cos ^{2} x}-\frac{3}{\sin x \cdot \cos x}$
When $\cos x=\frac{1}{\sqrt{3}} ; \sin x=\frac{\sqrt{2}}{\sqrt{3}}$
$\therefore f^{\prime}\left(\frac{1}{\sqrt{3}}\right) \frac{1}{\sqrt{3}}=6-\frac{9}{\sqrt{2}}$
A
$1+6 \log _{ e}\left(\frac{6}{7}\right)$
B
$1-6 \log _{ e }\left(\frac{6}{7}\right)$
C
$\log _{e}\left(\frac{7}{6}\right)$
D
$1-7 \log _{ e }\left(\frac{6}{7}\right)$
Solution
$\int\limits_{0}^{1} \frac{1}{7^{\left[\frac{1}{x}\right]}} dx =-\int\limits_{1}^{0} \frac{1}{7^{\left[\frac{1}{x}\right]}} dx$
$=(-1)\left[\int\limits_{1}^{1 / 2} \frac{1}{7} dx +\int\limits_{1 / 2}^{1 / 3} \frac{1}{7^{2}} dx +\int\limits_{1 / 3}^{1 / 4} \frac{1}{7^{3}} dx +\ldots \ldots \infty\right] =\left(\frac{1}{7}+\frac{1}{2 \cdot 7^{2}}+\frac{1}{3 \cdot 7^{3}}+\ldots \infty\right)-\left(\frac{1}{7 \cdot 2}+\frac{1}{7^{2} \cdot 3}+\frac{1}{7^{2} \cdot 4} \ldots \infty\right)$
$=-\ln \left(1-\frac{1}{7}\right)-7\left(\frac{1}{7^{2} \cdot 2}+\frac{1}{7^{3} \cdot 3}+\frac{1}{7^{4} \cdot 4}+\ldots \ldots \infty\right)$
$={\left[\text{as} \ln (1+ x )= x -\frac{ x ^{2}}{2}+\frac{ x ^{3}}{3}-\frac{ x ^{4}}{4} \ldots \infty\right] }$
$\left[\right.$ as $\left.\ln (1-x)=-\left(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4} \ldots \infty\right)\right]$
$=6 \ln \frac{6}{7}-7\left(-\ln \left(1-\frac{1}{7}\right)-\frac{1}{7}\right)$
$=6 \ln \frac{6}{7}+1$
A
$2 e$
B
$\frac{2}{ e }$
C
$2$
D
$\frac{1}{ e }$
Solution
$\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}$
I.f $=e^{\int \frac{1}{1+y^{2}} d y}=e^{\tan ^{-1} y}$
$x e^{\tan ^{-1} y}=\int \frac{\tan ^{-1} y}{1+y^{2}} e^{\tan ^{-1} y} d y$
$x \cdot e ^{\tan ^{-1} y }=\left(\tan ^{-1} y -1\right) e ^{\tan ^{-1} y }+ c$
$\therefore (1,0)$ lies exit $c=2$.
For $y=\tan 1 \Rightarrow x=\frac{2}{ e }$
A
575
B
-575
C
576
D
-576
Solution
Vertex $(5,4)$
Directrix : $3 x+y-29=0$
Co-ordinates of $B$ (foot of directrix)
$\frac{x-5}{3}=\frac{y-4}{1}=-\left(\frac{15+4-29}{10}\right)=1$

$x=8, y=5$
$S=(2,3)$ (focus)
Equation of parabola
$P S=P M$
so equation is
$x^{2}+9 y^{2}-6 x y+134 x-2 y-711=0$
$a+b+c+d+k=9-6+134-2-711=-576$
A
An empty set
B
$\left(6, \frac{95}{9}\right]$
C
$\left[\frac{80}{9}, 10\right)$
D
$\left(9, \frac{92}{9}\right]$
Solution
$C: 4 x^{2}+4 y^{2}-12 x+8 y+k=0$
$\Rightarrow x^{2}+y^{2}-3 x+2 y+\left(\frac{k}{4}\right)=0$
Centre $\left(\frac{3}{2},-1\right) ; r=\sqrt{\frac{13-k}{2}}$
$\Rightarrow k \leq 13 \ldots$ (1)
(i) Point $\left(1, \frac{-1}{3}\right)$ lies on or inside circle $C$
$\Rightarrow S _{1} \leq 0 \Rightarrow k \leq \frac{92}{9}$ ...(2)
(ii) $C$ lies in $4^{\text {th }}$ quadrant

$r <1$
$\Rightarrow \frac{\sqrt{13- k }}{2}<1$
$\Rightarrow k <9 \ldots .(3)$
Hence $(1) \cap(2) \cap(3) \Rightarrow k \in\left(9, \frac{92}{9}\right]$
A
5
B
$\frac{50}{13}$
C
$4$
D
$\frac{63}{13}$
Solution

$\frac{ x +2}{4}=\frac{ y -1}{2}=\frac{ z +1}{3}=\lambda$
$( x , y , z )=(4 \lambda-2,2 \lambda+1,3 \lambda-1)$
$\overrightarrow{ AP }=(4 \lambda-3) \hat{ i }+(2 \lambda-1) \hat{ j }+(3 \lambda-5) \hat{ k }$
$\vec{ b }=4 \hat{ i }+2 \hat{ j }+3 \hat{ k }$
$\overrightarrow{ AP } \cdot \vec{ b }=0$
$4(4 \lambda-3)+2(2 \lambda-1)+3(3 \lambda-5)=0$
$29 \lambda=12+2+15=29$
$\lambda=1$
$P =(2,3,2)$
$3 x +4 y +12 z +23=0$
$d =\left|\frac{6+12+24+23}{\sqrt{9+16+144}}\right|$
$d =\left|\frac{65}{13}\right|=5$
A
$\frac{18}{\sqrt{5}}$
B
$\frac{22}{3 \sqrt{5}}$
C
$\frac{46}{3 \sqrt{5}}$
D
$6 \sqrt{3}$
Solution
$\frac{x-3}{2}=\frac{y-2}{3}=\frac{z-1}{-1}$
$\frac{ x +3}{2}=\frac{ y -6}{1}=\frac{ z -5}{3}$
$A =(3,2,1)$
$B=(-3,6,5)$
$\overrightarrow{n_{1}}=2 \hat{i}+3 \hat{j}-\hat{k}$
$\overrightarrow{n_{2}}=2 \hat{i}+\hat{j}-3 \hat{k}$
$\overrightarrow{ BA }=6 \hat{ i }-4 \hat{ j }-4 \hat{ k }$
SHORTEST DISTANCE $=\frac{\left[\overrightarrow{ BA } \overrightarrow{ n _{1}} \overrightarrow{ n _{2}}\right]}{\left|\overrightarrow{ n _{1}} \times \overrightarrow{ n _{2}}\right|}$
$\overrightarrow{ n _{1}} \times \overrightarrow{ n _{2}}=\begin{vmatrix} \hat{ i } & \hat{ j } & \hat{ k } \\ 2 & 3 & -1 \\ 2 & 1 & 3 \end{vmatrix}$
$=10 \hat{ i }-8 \hat{ j }-4 \hat{ k }$
${\left[\overrightarrow{ BA } \overrightarrow{ n _{1}} \overrightarrow{ n _{2}}\right]=60+32+16=108}$
$\left|\overrightarrow{ n _{1}} \times \overrightarrow{ n _{2}}\right|=\sqrt{100+64+16}=\sqrt{180}$
$S . D=\frac{108}{\sqrt{180}}=\frac{108}{6 \sqrt{5}}=\frac{18}{\sqrt{5}}$
A
$\frac{\pi}{4}$
B
$-\frac{\pi}{4}$
C
$\frac{5 \pi}{6}$
D
$\frac{3 \pi}{4}$
Solution

Area $=\frac{1}{2}|\vec{ a } \times \vec{ b }|=2 \sqrt{2}$
$\Rightarrow|\vec{ a } \times \vec{ b }|=4 \sqrt{2}$
$|\vec{ a }|=1 \text { and }|\vec{ a } \cdot \vec{ b }|=|\vec{ a } \times \overrightarrow{ b }|$
$\Rightarrow \cos \theta=\sin \theta$
$\Rightarrow \theta=\frac{\pi}{4}$
$\therefore|\vec{ a } \times \vec{ b }|=4 \sqrt{2}$
$\Rightarrow|\vec{ a }||\vec{ b }| \sin \frac{\pi}{4}=4 \sqrt{2}$
$\Rightarrow|\vec{ b }|=8$
Now, $\vec{ c }=2 \sqrt{2}(\vec{ a } \times \vec{ b })-2 \vec{ b }$
$|\vec{ c }|=\sqrt{(2 \sqrt{2})^{2}|\vec{ a } \times \vec{ b }|^{2}+(2|\vec{ b }|)^{2}}=16 \sqrt{2}$
Now, $\vec{ b } \cdot \vec{ c }=-2|\vec{ b }|^{2}$
$\Rightarrow 8 \times 16 \sqrt{2} \times \cos \alpha=-2.64$
$\Rightarrow \cos \alpha=-\frac{1}{\sqrt{2}}$
$\Rightarrow \alpha=\frac{3 \pi}{4}$
A
162
B
320
C
674
D
420
Solution
mean $\bar{x}=\frac{4+5+6+6+7+8+x+y}{8}=6$
$\Rightarrow x+y=48-36=12$
Variance
$=\frac{1}{8}\left(16+25+36+36+49+64+x^{2}+y^{2}\right)-36=\frac{9}{4}$
$\Rightarrow x^{2}+y^{2}=80$
$\therefore x=4 ; y=8$
$x^{4}+y^{2}=256+64=320$
A
$\frac{1}{6}$
B
$\frac{5}{6}$
C
$\frac{2}{3}$
D
$\frac{6}{7}$
Solution
Required probability $=\frac{\text{ar}( ADEC )}{\text{ar}( ABC )}$

$=1-\frac{\text{ar}( BDE )}{\text{ar}( ABC )}$
$=1-\frac{\frac{1}{2} \times 2 \times 4}{\frac{1}{2} \times 8 \times 6}=1-\frac{1}{6}=\frac{5}{6}$
A
$\frac{26}{25}$
B
$\frac{25}{26}$
C
$\frac{50}{51}$
D
$\frac{52}{51}$
Solution
$\tan ^{-1} \frac{1}{1+n+n^{2}}=\tan ^{-1}\left(\frac{(n+1)-n}{1+n(n+1)}\right)$
$=\tan ^{-1}(n+1)-\tan ^{-1} n$
so, $\displaystyle\sum_{n=1}^{50}\left(\tan ^{-1}(n+1)-\tan ^{-1} n\right)$
$=\tan ^{-1} 51-\tan ^{-1} 1$
$\cot \left(\displaystyle\sum_{n=1}^{50} \tan ^{-1}\left(\frac{1}{1+n+n^{2}}\right)\right)=\cot \left(\tan ^{-1} 51+\tan ^{-1} 1\right)$
$=\frac{1}{\tan \left(\tan ^{-1} 51-\tan ^{-1} 1\right)}=\frac{1+51 \times 1}{51-1}$
$=\frac{52}{50}=\frac{26}{25}$
A
$10 x^{4}-10 x^{2}-5=0$
B
$16 x^{4}+20 x^{2}-5=0$
C
$16 x^{4}-20 x^{2}+5=0$
D
$16 x^{4}-10 x^{2}+5=0$
Solution
$\cos 72^{\circ}=\frac{\sqrt{5}-1}{4}$
$\Rightarrow 1-2 \sin ^{2} 36^{\circ}=\frac{\sqrt{5}-1}{4}$
$\Rightarrow 4-8 \alpha^{2}=\sqrt{5}-1$
$\Rightarrow 5-8 \alpha^{2}=\sqrt{5}$
$\Rightarrow \left(5-8 \alpha^{2}\right)^{2}=5$
$\Rightarrow 25+64 \alpha^{4}-80 \alpha^{2}=5$
$\Rightarrow 64 \alpha^{4}-80 \alpha^{2}+20=0$
$\Rightarrow 16 \alpha^{4}-20 \alpha^{2}+5=0$
A
$((\sim q) \wedge p) \wedge q$
B
$((\sim q ) \wedge p ) \wedge( p \wedge(\sim p ))$
C
$((\sim q ) \wedge p ) \vee( p \vee(\sim p ))$
D
$( p \wedge q ) \wedge(\sim( p \wedge q ))$
Solution
$( A )(\sim q \wedge p ) \wedge q =(\sim q \wedge q ) \wedge p = f$
(B) $(\sim q \wedge p ) \wedge( p \wedge \sim p )=\sim q \wedge( p \wedge \sim p )= f$
(C) $(\sim q \wedge p ) \vee( p \vee \sim p )=(\sim q \wedge p ) \vee( t )= t$
(D) $( p \wedge q ) \wedge(\sim( p \wedge q ))= f$
Answer: 190
Solution
$f ^{-1}( n )=\begin{cases}\frac{ n }{2} & ; n =2,4,6,8,10 \\ \frac{ n +11}{2} & ; \quad n =1,3,5,7,9\end{cases}$
$f ( g ( n ))= \begin{cases} n +1 & ; n \in \text { odd } \\ n -1 & ; \quad n \in \text { even }\end{cases}$
$g ( n )= \begin{cases} f ^{-1}( n +1) & ; n \in \text { odd } \\ f ^{-1}( n -1) & ; \quad n \in \text { even }\end{cases}$
$g ( n )= \begin{cases}\frac{ n +1}{2} ; & n \in \text { odd } \\ \frac{ n +10}{2} ; & n \in \text { even }\end{cases}$
$g (10) \cdot\left[ g (1)+ g (2)+ g (3)+ g (4)+ g (5)\right]$
$=10 \cdot\left[1+6+2+7+3]=190\right]$
Answer: 98
Solution
$x^{2}-4 \lambda x+5=0\left\langle_{\beta}^{\alpha}\right.$
$x^{2}-(3 \sqrt{2}+2 \sqrt{3}) x+(7+3 \lambda \sqrt{3})=0\left\langle_{\gamma}^{\alpha}\right.$
$\alpha+\beta=4 \lambda$
$\alpha+\gamma=3 \sqrt{2}+2 \sqrt{3}$
$\beta+\lambda=3 \sqrt{2}$
$\therefore \alpha=2 \lambda+\sqrt{3}$
$\beta=2 \lambda-\sqrt{3}$
$\alpha \gamma=7+3 \lambda \sqrt{3}$
$\alpha \beta=5$
$4 \lambda^{2}=8 \Rightarrow \lambda=\sqrt{2}$
$\therefore (\alpha+2 \beta+\lambda)^{2}=(4 \alpha+3 \sqrt{2})^{2}=(7 \sqrt{2})^{2}=98$
Answer: 180
Solution
Let $A=\begin{bmatrix} a & b \\ c & d \end{bmatrix} ; a , b , c , d \in\{0,1,2,3,4,5\}$ $a+b+c+d=p, p \in\{3,5,7\}$
Case-(i)
$a+b+c+d=3 ; a, b, c, d \in\{0,1,2,3\}$
No. of ways $={ }^{3+4-1} C _{4-1}={ }^{6} C _{3}=56$ ...(1)
Case-(ii)
$a+b+c+d=5 ; a, b, c, d \in\{0,1,2,3,4,5\}$
No. of ways $={ }^{3+4-1} C _{4-1}={ }^{8} C _{3}=56$ ...(2)
Case-(iii)
$a+ b+ c+ d=7$
No. of ways $=$ total ways when $a, b, c, d \in\{0,1,2$, $3,4,5,6,7\}$ - total ways when a, b, c, d $\notin\{6,7\}$
No of ways $={ }^{7+4-1} C_{4-1}=\left(\frac{\lfloor 4}{\lfloor 3}+\frac{4}{\underline{2}}\right)$
$={ }^{10} C _{3}-16=104$
Hence total no. of ways $=180$
Answer: 57
Solution
coefficients and there cumulative sum are:
Coefficient
Commulative sum
$x ^{7 n } \rightarrow{ }^{7} C _{0}$
1
$x ^{6 n -5} \rightarrow 2 \cdot{ }^{7} C _{1}$
1+14
$x ^{5 n -10} \rightarrow 2^{2} \cdot{ }^{7} C _{2}$
1 + 14+ 84
$ x ^{4 n -15} \rightarrow 2^{3} \cdot{ }^{7} C _{3}$
1+ 14+ 84+280
$ x ^{3 n -20} \rightarrow 2^{4} \cdot{ }^{7} C _{4}$
1+ 4+ 84+280+560 =939
$ x ^{2n -25} \rightarrow 2^{5} \cdot{ }^{7} C _{5}$
$3 n -20 \geq 0 \cap 2 n -25<0 \cap n \in I$
$\therefore 7 \leq n \leq 12$
Sum $=7+8+9+10+11+12=57$
| Coefficient | Commulative sum |
|---|---|
| $x ^{7 n } \rightarrow{ }^{7} C _{0}$ | 1 |
| $x ^{6 n -5} \rightarrow 2 \cdot{ }^{7} C _{1}$ | 1+14 |
| $x ^{5 n -10} \rightarrow 2^{2} \cdot{ }^{7} C _{2}$ | 1 + 14+ 84 |
| $ x ^{4 n -15} \rightarrow 2^{3} \cdot{ }^{7} C _{3}$ | 1+ 14+ 84+280 |
| $ x ^{3 n -20} \rightarrow 2^{4} \cdot{ }^{7} C _{4}$ | 1+ 4+ 84+280+560 =939 |
| $ x ^{2n -25} \rightarrow 2^{5} \cdot{ }^{7} C _{5}$ |
Answer: 3
Solution
$f ( x )=[1+ x ]+\frac{\alpha^{2[ x ]+\{x\}}+[ x ]-1}{2[ x ]+\{ x \}}$
$\displaystyle\lim _{ x \rightarrow 0^{-}} f ( x )=\alpha-\frac{4}{3}$
$\Rightarrow 0+\frac{\alpha^{-1}-2}{-1}=\alpha-\frac{4}{3}$
$\Rightarrow 2-\frac{1}{\alpha}=\alpha-\frac{4}{3}$
$\Rightarrow \alpha+\frac{1}{\alpha}=\frac{10}{3}$
$\Rightarrow \alpha=3 ; \alpha \in I$
Q26. If $y(x)=\left(x^{x^{x}}\right), x > 0$ then $\frac{d^{2} x}{d y^{2}}+20$ at $x=1$ is equal to:
Answer: 16
Solution
$y =( x )=\left( x ^{ x }\right)^{ x }$
$\ln y ( x )= x ^{2} \cdot \ln x$
$\frac{1}{ y ( x )} \cdot y ^{\prime}( x )=\frac{ x ^{2}}{ x }+2 x \cdot \ln x$
$y ^{\prime}( x )= y ( x )[ x +2 x \ln x ]$
$y (1)=1 ; y ^{\prime}(1)=1$
$y ^{\prime \prime}( x )= y ^{\prime}( x )[ x +2 x \cdot \ln ( x )] + y ( x )[1+2(1+\ln x )]$
$y ^{\prime \prime}(1)=1[1+0]+1(1+2)=4$
$\frac{ d ^{2} y }{ dx ^{2}}=-\left(\frac{ dy }{ dx }\right)^{3} \cdot \frac{ d ^{2} x }{ dy ^{2}}$
$\Rightarrow 4=-\frac{ d ^{2} x }{ dy ^{2}}$
$\frac{ d ^{2} x }{ dy }=-4$
$-4+20=16$
Answer: 36
Solution

$A =\frac{3}{2} \int\limits_{0}^{1}\left(1- x ^{2 / 3}\right)^{3 / 2} dx$
Let $x =\sin ^{3} \theta$
$A =\frac{3}{2} \int\limits_{0}^{\pi / 2}\left(1-\sin ^{2} \theta\right)^{3 / 2} \cdot 3 \sin ^{2} \theta \cos \theta d \theta$
$=\frac{3}{2} \int\limits_{0}^{\pi / 2} 3 \sin ^{2} \theta \cos ^{4} \theta d \theta$
$=\frac{9}{2} \int\limits_{0}^{\pi / 2} \sin ^{2} \theta \cos ^{4} \theta d \theta$
$A =\frac{9}{2} \times \frac{1.3 .1}{(2+4)(4)(2)} \cdot \frac{\pi}{2}$
$\Rightarrow A =\frac{9 \pi}{64}$
$\Rightarrow \frac{64 A }{\pi}=9$
$\Rightarrow \frac{256 A }{\pi}=36$
Answer: 320
Solution
$\left(1-x^{2}\right) \frac{d y}{d x}=x y+\left(x^{3}+2\right) \sqrt{1-x^{2}}$
$\Rightarrow \frac{d y}{d x}+\left(\frac{-x}{1-x^{2}}\right) y=\frac{x^{3}+2}{\sqrt{1-x^{2}}}$
$I F=e^{\int \frac{-x}{1-x^{2}} d x}=\sqrt{1-x^{2}}$
$y(x) \cdot \sqrt{1-x^{2}}=\frac{x^{4}}{4}+2 x+c$
$y(0)=0 \Rightarrow c=0$
$\sqrt{1-x^{2}} y (x)=\frac{x^{4}}{4}+2 x$
required value $=\int\limits_{-1 / 2}^{1 / 2}\left(\frac{x^{4}}{4}+2 x\right) d x-\frac{1}{4} \cdot 2 \int\limits_{0}^{1 / 2} x^{4} d x$
$=\frac{1}{10}\left(x^{5}\right)_{0}^{1 / 2}=\frac{1}{320}$
$k ^{-1}=320$
Answer: 11
Solution
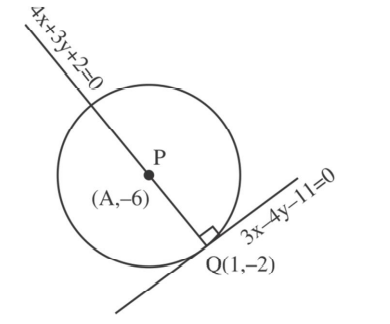
$4 x+3 y+2=0$
$3 x-4 y-11=0$
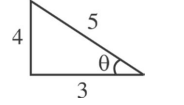
$\frac{x}{-25}=\frac{y}{50}=\frac{1}{-25}$
$\frac{x-1}{\cos \theta}=\frac{y+2}{\sin \theta}=\pm 5$
$y=-2+5\left(-\frac{4}{5}\right)=-6$
$x=1+5\left(\frac{3}{5}\right)=4$
Req $\cdot$ distance
$\left|\frac{5(4)-12(-6)+51}{13}\right|$
$=\left|\frac{20+72+51}{13}\right|$
$=\frac{143}{13}=11$
Answer: 19