JEE Main Physics Question Paper with Solution 2023 June 25th Shift 2 - Evening
A
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$.
B
Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$.
C
$A$ is true but $R$ is false
D
$A$ is false but $R$ is true
Solution

$h _{1}=\frac{ u ^{2} \sin ^{2} \theta_{1}}{2 g } h _{2}=\frac{ u ^{2} \sin ^{2} \theta_{2}}{2 g }$
$h _{1} h _{2}=\frac{ u ^{2} \sin ^{2} \theta_{1}}{2 g } \times \frac{ u ^{2} \sin ^{2} \theta_{2}}{2 g }$
$\theta_{2}=90-\theta_{1}$
$h _{1} h _{2}=\frac{ u ^{2} \sin ^{2} \theta_{1}}{2 g } \cdot \frac{ u ^{2} \cos ^{2} \theta_{1}}{2 g }$
$=\left[\frac{ u ^{2} \sin \theta_{1} \cos \theta_{1}}{2 g }\right]^{2}$
$=\left[\frac{ u ^{2} \sin \theta_{1} \cos \theta_{1}}{2 g } \times \frac{2}{2}\right]^{2}=\frac{ R ^{2}}{16}$
$R =4 \sqrt{ h _{1} h _{2}}$
So R is correct explanation of A
A
$\frac{\alpha- f }{1+\beta}$
B
$\frac{\alpha+f}{2(\beta-1)}$
C
$\frac{\alpha+ f }{2(1+\beta)}$
D
$\frac{f-\alpha}{2(1+\beta)}$
Solution
$X_{P}(t)=\alpha t+\beta t^{2}$
$X_{Q}=f t-t^{2}$
$V_{P}(t)=\alpha+2 \beta t$
$V_{Q}=f-2 t$
$V_{P}=V_{Q}$
$\alpha+2 \beta t=f-2 t$
$t=\frac{f-\alpha}{2 \beta+2}$
A
$R \leq \frac{\mu g }{2 \omega^{2}}$
B
$R \leq \frac{\mu g }{\omega^{2}}$
C
$R \geq \frac{\mu g }{2 \omega^{2}}$
D
$R \geq \frac{\mu g }{\omega^{2}}$
Solution
For beaker to move with disc
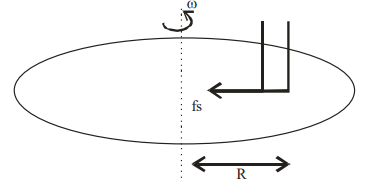
$f_{s}=m \omega^{2} R$
We know that $f _{ s } \leq f _{ s \max }$
$m \omega^{2} R \leq \mu m g$
$R \leq \frac{\mu g }{\omega^{2}}$
A
$2.4 \times 10^{6} \,cm ^{3}$
B
$1.2 \times 10^{5} \,cm ^{3}$
C
$6.0 \times 10^{4}\, cm ^{3}$
D
$4.8 \times 10^{5}\, cm ^{3}$
Solution
Increase in volume $\Delta V =\gamma V _{0} \Delta T$
$\gamma=3 \alpha$
So $\Delta V =(3 \alpha) V _{0} \Delta T$
Total surface area $=6 a ^{2}$,
where $a$ is side length $24=6 a ^{2} \,\,\, a =2 m$
Volume $V _{0}=(2)^{3}=8 m ^{3}$
$\Delta V =\left(3 \times 5 \times 10^{-4}\right)(8) \times 10 $
$=1.2 \times 10^{5} cm ^{3}$
A
1.5 kg
B
5.8 kg
C
2.9 kg
D
3.8 kg
Solution
Heat given by block to get $0^{\circ} C$ temperature
$\Delta Q_{1}=5 \times\left(0.39 \times 10^{3}\right) \times(500-0)$
$=975 \times 10^{3} J$
Heat absorbed by ice to melt mass
$\Delta Q _{2}= m \times\left(335 \times 10^{3}\right) J $
$\Delta Q _{1}=\Delta Q _{2}$
$ m \times\left(335 \times 10^{3}\right)=975 \times 10^{3} $
$ m =\frac{975}{335}=2.910\, kg$
A
$\left(1+\frac{ f }{3}\right)$
B
$\left(1+\frac{2}{ f }\right)$
C
$\left(1+\frac{ f }{2}\right)$
D
$\left(1+\frac{1}{f}\right)$
Solution
Molar heat capacity at constant volume $C _{ V }=\frac{f R }{2}$
where $f$ is degree of freedom.
Molar heat capacity at constant pressure can be written as
$C _{ P }= R + C _{ V }= R +\frac{ fR }{2}=\left(1+\frac{ f }{2}\right) R$
So $\frac{C_{P}}{C_{v}}=1+\frac{2}{f}$
A
$-\frac{v^{2}}{R} \sin \theta \hat{i}+\frac{v^{2}}{R} \cos \theta \hat{j}$
B
$-\frac{v^{2}}{R} \cos \theta \hat{i}+\frac{v^{2}}{R} \sin \theta \hat{j}$
C
$-\frac{v^{2}}{R} \cos \theta \hat{i}-\frac{v^{2}}{R} \sin \theta \hat{j}$
D
$-\frac{v^{2}}{R} \hat{i}+\frac{v^{2}}{R} \hat{j}$
Solution
$a =|\text{ a }|=\frac{ V ^{2}}{ R }$

$\vec{a}=-a \cos \theta \hat{i}-a \sin \theta \hat{j}$
$=-\frac{V^{2}}{R} \cos \theta \hat{i}-\frac{V^{2}}{R} \sin \theta \hat{j}$
A
$2: 1$
B
$1:2$
C
$1: 4$
D
$4: 1$
Solution
$C _{1}=\frac{\epsilon_{0} A }{ d }$
$C _{2}=\frac{\epsilon_{0} A }{\frac{ d }{2}+\frac{ d / 2}{\propto}}=\frac{2 \epsilon_{0} A }{ d }$
$\frac{ C _{2}}{ C _{1}}=\frac{2}{1}$
A
$r _{2}- r _{1}$
B
$r_{1}-r_{2}$
C
$r _{1}$
D
$r _{2}$
Solution
$I=\frac{2 E}{R+r_{1}+r_{2}} \ldots \ldots( i )$
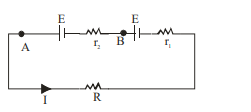
But $V _{ A }- V _{ B }= E - Ir _{2}=0$
$\Rightarrow I=\frac{E}{r_{2}} \ldots \ldots( ii )$
Comparing values of I from (i) and (ii)
$\frac{E}{r_{2}}=\frac{2 E}{R+r_{1}+r_{2}}$
$\Rightarrow R=r_{2}-r_{1}$
A
Both statement - I and statement - II are true.
B
Both statement - I and Statement - II are false.
C
Statement - I is true but statement - II is false.
D
Statement-I is false but Statement-II is true.
Solution
According to curie's law, magnetic susceptibility is inversely proportional to temperature for a fixed value of external magnetic field i.e. $\chi=\frac{C}{T}$.
The same is applicable for ferromagnet & the relation is given as $\chi=\frac{ C }{ T - T _{ C }} \left( T _{ C }\right.$ is curie temperature)
Diamagnetism is due to non-cooperative behaviour of orbiting electrons when exposed to external magnetic field.
A
$B$
B
$2 B$
C
$4 B$
D
$\frac{B}{2}$
Solution
$B _{1}=\mu_{0} nI$
$B _{2}=\mu_{0}\left(\frac{ n }{2}\right)(2 I )$
$\Rightarrow B _{1}= B _{2}$
A
$\tan ^{-1}(0.17)$
B
$\tan ^{-1}(9.46)$
C
$\tan ^{-1}(0.30)$
D
$\tan ^{-1}(13.33)$
Solution
$X _{ L }=10^{-2} \times 3000=30\, \Omega$
$X _{ C }=\frac{1}{3000 \times 25 \times 10^{-6}}=\frac{40}{3} \Omega$
$X = X _{ L }- X _{ C }$
$=30-\frac{40}{3}=\frac{50}{3}$
$\tan \delta=\frac{ X }{ R }=\frac{50}{3 \times 100}=\frac{1}{6}$
$\delta=\tan ^{-1}\left(\frac{1}{6}\right)=\tan ^{-1}(0.17)$
A
$2.25$
B
$4.25$
C
$6.25$
D
$8.25$
Solution
Given,
Speed of electromagnetic waves, $v=2 \times 10^8 m / s$
Relative permeability of the medium $=1$
Speed of light, $C=3 \times 10^8 m / s$
Using the formula of speed of electromagnetic wave in a medium,
$
\begin{array}{l}
v=\frac{1}{\sqrt{\mu \varepsilon}} \\
v=\frac{1}{\sqrt{\mu_0 \mu_r\left(\varepsilon_0 \varepsilon_r\right)}} \\
v=\frac{1}{\sqrt{\mu_0 \varepsilon_0}} \times \frac{1}{\sqrt{\mu_{ r } \varepsilon_{ r }}}
\end{array}
$
Therefore,
Relative permittivity,
$
\begin{aligned}
\varepsilon_r & =\frac{c^2}{v^2 \mu_r} \\
& =\frac{\left(3 \times 10^8\right)^2}{\left(2 \times 10^8\right)^2 \times 1} \\
& =2.25
\end{aligned}
$
A
3
B
4
C
2
D
1
Solution
$\frac{ I _{1}}{ I _{2}}=4$
$\frac{ I _{\max }}{ I _{\min }}=\left[\frac{\sqrt{ I _{1}}+\sqrt{ I _{2}}}{\sqrt{ I _{1}}-\sqrt{ I _{2}}}\right]^{2}$
$\frac{ I _{\max }}{ I _{\min }}=\left[\frac{2 \sqrt{ I _{2}}+\sqrt{ I _{2}}}{2 \sqrt{ I _{2}}-\sqrt{ I _{2}}}\right]^{2}$
$\frac{ I _{\max }}{ I _{\min }}=9$
$\frac{ I _{\max }}{ I _{\max }- I _{\min }}=\frac{10}{8}$
$\frac{5}{ x }=\frac{10}{8}$
$x =4$
A
Reflected and refracted rays will be perpendicular to each other
B
Wave will propagate along the surface of prism
C
No refraction, and there will be total reflection of light.
D
No reflection and there will be total transmission of light.
Solution

But as the incident light electric field vectors are completely removed so there will be no reflection and there will be total transmission of light, explained by an experiment in NCERT.
[Reference NCERT Part-2 Pg-380, (A special case of total transmission)]
Note : Since direction of polarization is not mentioned hence most suitable option (D) corresponding to case in which electric field is absent perpendicular to plane consisting incident and normal.
A
$\lambda_{ p }=\lambda_{ n } >\lambda_{ e } >\lambda_{\alpha}$
B
$\lambda_{\alpha} < \lambda_{ n }< \lambda_{ p }< \lambda_{ e }$
C
$\lambda_{ e }< \lambda_{ p }=\lambda_{ n } >\lambda_{\alpha}$
D
$\lambda_{ e }=\lambda_{ p }=\lambda_{ n }=\lambda_{\alpha}$
Solution
$\lambda=\frac{ h }{\sqrt{2 Em }}$
$\lambda \propto \frac{1}{\sqrt{ m }}$
$\therefore \lambda_{ e }>\lambda_{ p }>\lambda_{ n }>\lambda_{\alpha}$
A

B

C

D

Solution
$R = R _{0} A ^{\frac{1}{3}}$
$\ln \frac{ R }{ R _{0}}=\frac{1}{3} \ln A$

A
AND gate
B
OR gate
C
NOR gate
D
NAND gate
Solution
$=[\overline{[\overline{ A + A }]+[\overline{ B + B }]}]$
$Y =\overline{\overline{ A }+\overline{ B }}\left( D ^{\prime}\right.$ MORGAN LAW)
$Y = AB$
A
A-IV, B-III, C-II, D-I
B
A-I, B-IV, C-II, D-III
C
A -IV, B-II, C-III, D-I
D
A-I, B-II, C-III, D-IV
Solution
Question based on the theory given in NCERT.
A
$\frac{ KS }{( S + G )}$
B
$\frac{( G + S )}{ nKS }$
C
$\frac{ nKS }{( G + S )}$
D
$\frac{ nK ( G + S )}{ S }$
Solution

Figure of merit $\frac{I_{g}}{\theta}=K$
$ I _{ g }= Kn $
$I =\frac{ I _{ g }}{ s }( G + S ) $
$I =\frac{ nK }{ S }( G + S )$
Answer: 18
Solution
$z=a^{2} x^{3} y^{1 / 2} $
$\frac{\Delta z }{ z }=\frac{2 \Delta a }{ a }+\frac{3 \Delta x }{ x }+\frac{1}{2} \frac{\Delta y }{ y }$
$a$ is constant
$\frac{\Delta z }{ z } \times 100=3(4 \%)+\frac{1}{2}(12 \%)=18 \%$
Answer: 24
Solution
$f _{ s \max }=\frac{ mv ^{2}}{ R }$
$\mu mg =\frac{ mv { }^{2}}{ R }$
$v =\sqrt{\mu Rg }$
$\frac{ v _{2}}{ v _{1}}=\sqrt{\frac{ R _{2}}{ R _{1}}}$
$\frac{ v _{2}}{30}=\sqrt{\frac{48}{75}}$
$v _{2}=24 \,m / s$
Answer: 12
Solution
$mg =2 N$

$\sqrt{x} \frac{1}{2}=\frac{2 \sqrt{3}}{2}$
$x=12$
Answer: 5
Solution
$I _{1}=\frac{2}{5} M (2 R )^{2}=\frac{8}{5} MR ^{2}$
$I _{1}=\frac{1}{2} M (2 R )^{2}=2 MR ^{2}$
$I _{3}=\frac{ M (2 R )^{2}}{4}= MR ^{2}$
$I _{4}=\frac{ M (2 R )^{2}}{2}=2 MR ^{2}$
$2\left( I _{2}+ I _{3}\right)+ I _{4}=x I _{1}$
$8 MR ^{2}= x \frac{8}{5} MR ^{2}$
$x =5$
Answer: 2
Solution
$V =\frac{ GM }{ r } \Rightarrow \frac{ V _{1}}{ V _{2}}=\sqrt{\frac{800}{3200}}=\frac{1}{2}$
Answer: 250
Solution
$pV = nRT$
$\Delta P . V = nR \Delta T$
$\Rightarrow \frac{\Delta P }{ P }=\frac{\Delta T }{ T }=\frac{0.4}{100} $
$\Rightarrow T =\frac{100 \times 1}{0.4}=250\, K$
Answer: 198
Solution
$q \rightarrow nq$
$n \frac{4}{3} \pi r ^{3}=\frac{4}{3} \pi\left( r ^{\prime}\right)^{3}$
$\Rightarrow r ^{\prime}= n ^{\frac{1}{3} r }$
$V =\frac{ kq }{ r } \propto \frac{ n }{ n ^{1 / 3}} \propto n ^{2 / 3} \propto 27^{2 / 3} $
$\Rightarrow v ^{\prime}=9 V =9 \times 22=198$
Answer: 300
Solution
$V ^{\prime}= V$
$\ell^{\prime} A =\ell A$
$2 \ell A ^{\prime}=\ell A$
$A ^{\prime}=\frac{ A }{2}$
$R =\rho \frac{\ell}{ A } \ldots$ (i)
$\ell^{\prime}=2 \ell$
$A ^{\prime}=\frac{ A }{2}$
$R ^{\prime}=\frac{\rho \ell^{\prime}}{ A ^{\prime}}=\frac{\rho 2 \ell}{\frac{ A }{2}}$
$R ^{\prime}=\frac{4 \rho \ell}{ A }$
$R^{\prime}=4 R$ from equation (i)
$\%$ increase in resistance
$=\frac{ R ^{\prime}- R }{ R } \times 100=\frac{4 R - R }{ R } \times 100 $
$=300 \%$
Answer: 22
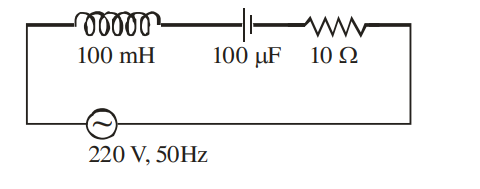
Solution
$X _{ L }=\omega L =2 \pi \times 50 \times 10^{-1}=10 \pi$
$X _{ X }=\frac{1}{\omega C }=\frac{1}{2 \pi \times 50} \times 10^{4}=\frac{100}{\pi}$
$R =10 \Omega$
$Z =\sqrt{\left(10 \pi-\frac{100}{\pi}\right)^{2}+10^{2}} \simeq 10 \Omega$
$i =\frac{ E }{2} \simeq \frac{220}{10} \simeq 22 \,Amp$
Answer: 15
Solution
Voltage Gain $=\frac{ I _{ C }}{ I _{ B }} \times \frac{ R _{0}}{ R _{ I }}=\frac{10 \times 10^{-3}}{200 \times 10^{-6}} \times \frac{60}{200}=15$
JEE Main Chemistry Question Paper with Solution 2023 June 25th Shift 2 - Evening
A
$3.21 \times 10^{-14} J$
B
$6.24 \times 10^{-16} J$
C
$8.58 \times 10^{-19} J$
D
$9.76 \times 10^{-20} J$
Solution
$W = h v $
$=6.6 \times 10^{-34} \times 1.3 \times 10^{15} $
$=8.58 \times 10^{-19}\, J $
A
$+324 \,kJ\,mol ^{-1}$
B
$+632 \,kJ \,mol ^{-1}$
C
$-632 \,kJ \,mol ^{-1}$
D
$-732 \,kJ \,mol ^{-1}$
Solution
$\Delta H =\sum \Delta H _{\text {Combustion }} ($ Reactant $)-\sum \Delta H _{\text {Combustion }}$(Product)
$=3 \times(-1300)-[-3268]$
$=-632 \,kJ \,mol ^{-1}$
A
$50 \%$
B
$60 \%$
C
$70 \%$
D
$80 \%$
Solution
$\Delta T = i k _{ f } \times m$
$0.2= i \times 1.86 \times \frac{0.7}{93} \times \frac{1000}{42}$
$i =\frac{0.2 \times 93 \times 6}{1.86 \times 100}$
$i =0.60$

$i =1-\alpha+\frac{\alpha}{2}$
$i =1-\frac{\alpha}{2}$
$1-\frac{\alpha}{2}=0.60$
$1-0.60=\frac{\alpha}{2}$
$\alpha=0.80$
A
$1.0 \times 10^{-15}$
B
$2.7 \times 10^{-12}$
C
$3.2 \times 10^{-10}$
D
$4.2 \times 10^{-8}$
Solution

$ k _{ sp } =(2 s )^{2}(3 s )^{3} $
$=4 s ^{2} \times 27( s )^{3} $
$=108( s )^{5} $
$( s )^{5} =\frac{1.08 \times 10^{-73}}{108} $
$ \Rightarrow s =10^{-15}$
A
A-II, B-III, C-I, D-IV
B
A-II, B-III, C-IV, D-I
C
A-III, B-II, C-IV, D-I
D
A-III, B-II, C-I, D-IV
Solution
Zymase naturally occurs in yeast.
Diastase is found in malt.
Urease is found in soyabean
Pepsin is found in stomach
A
F < Cl < Te < Po
B
Po < Te < F < Cl
C
Te < Po < Cl < F
D
Cl < F < Te < Po
Solution
As $Cl$ has maximum electron affinity among all elements.
Element
$\Delta_{\text {eg }} H ( k J / m o l )$
F
-328
Cl
-349
Te
-190
Po
-174
| Element | $\Delta_{\text {eg }} H ( k J / m o l )$ |
|---|---|
| F | -328 |
| Cl | -349 |
| Te | -190 |
| Po | -174 |
A
Both Statement I and Statement II are true.
B
Both Statement I and Statement II are false.
C
Statement I is true but Statement II is false.
D
Statement I is false but Statement II is true.
Solution
In the electro-refining, impure metal (here blister copper) is used as an anode while precious metal like $Au$, Pt get deposited as anode mud.
A
Both A and R are true and R is the correct explanation of A.
B
Both A and R are true but R is NOT the correct explanation of A.
C
A is true but R is false.
D
A is false but R is true.

A
A > C > B > D > E
B
A > B > C > D > E
C
A > C > B > E > D
D
A > B > C > E > D
Solution
$E _{ Cl _{2} / Cl ^{-}}^{\circ}=+1.36 \,V$
$E _{ I _{2} / I ^{-}}^{\circ}=+0.54 \,V$
$E _{ Ag ^{+} / Ag }^{\circ}=+0.80\, V$
$E _{ Na ^{+} / Na }^{\circ}=-2.71 \,V$
$E _{ Li ^{+} / Li ^{\circ}}^{\circ}=-3.05\, V$
A
$V ^{2+}$
B
$Ni ^{2+}$
C
$Cr ^{2+}$
D
$Fe ^{2+}$
Solution
$V^{2+}: 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{3}$
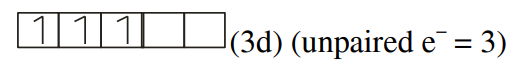

A
Both A and R are correct and R is the correct explanation of A.
B
Both A and R are correct but R is NOT the correct explanation of A.
C
A is correct but R is not correct.
D
A is not correct but R is correct.
Solution
Clean water have $BOD$ less than $5\, ppm$ while highly polluted water has $BOD$ greater or equal to $17 \,ppm$. So, assertion is correct. $BOD$ is measure of oxygen required to oxidise only bio-degradable organic matter. So, reason is false.
A
Both A and R are true and R is the correct explanation of A.
B
Both A and R are true but R is NOT the correct explanation of A.
C
A is true but R is false.
D
A is false but R is true.
Solution
Benzoic acid and Napthalene can be effectively separated by crystallization. Benzoic acid is soluble in hot water whereas Napthalene is insoluble.
A
remove unreacted sodium
B
decompose cyanide or sulphide of sodium
C
extract halogen from organic compound
D
maintain the $pH$ of extract
Solution
Sodium fusion extract is boiled with concentrated $HNO _{3}$ to remove sodium cyanide and sodium sulphide
A
benzyl bromide
B
bromobenzene
C
cyclohexyl bromide
D
methyl bromide

A

B

C

D

Solution
Enamine formation is an example of nucleophilic addition elimination reaction

Group is highly sterically hindered hence attack of nucleophile will not be possible.
A
Bithionol
B
Terpineol
C
Chloroxylenol
D
Chloramphenicol

Answer: 25
Solution
$0.30 \%$ glycine is equal to $75$
$1 \% \longrightarrow \frac{75}{0.30} $
$100 \% \longrightarrow \frac{75}{0.30} \times 100 $
$=25000\, g$
Answer: 32
Solution
$\frac{ P _{1}}{ T _{1}}=\frac{ P _{2}}{ T _{2}}$
$\frac{30}{300}=\frac{ P _{2}}{318}$
$P _{2}=\frac{30}{300} \times 318$
$=\frac{1}{10} \times 318$
$=32$
Answer: 3
Solution
$BeF _{2}, BF _{3}$ and $CCl _{4} \Rightarrow \mu_{\text {net }}=0$
$H _{2} O , NH _{3} \text { and } HCl \Rightarrow \mu_{\text{net }} \neq 0$
Answer: 0
Solution
$t _{1 / 2} \times \frac{1}{\left[ P _{0}\right]^{ n -1}}$
$\frac{ t _{1}}{ t _{2}}=\frac{\left( P _{2}\right)^{ n -1}}{\left( P _{1}\right)^{ n -1}}$
$\frac{340}{170}=\left(\frac{27.8}{55.5}\right)^{ n -1}$
$\Rightarrow 2=\frac{1}{(2)^{ n -1}}$
$n =0$
Answer: 20
Solution
$Fe ^{3+}+3 e ^{-} \longrightarrow Fe$
$3 F \longrightarrow 1$ mole $Fe$ is deposited
For $56\, g \longrightarrow 3 \times 96500$ (required charge)
For $1 \,g \longrightarrow \frac{3 \times 96500}{56}$ (required charge)
For $0.3482 \,g \longrightarrow \frac{3 \times 96500}{56} \times 0.3482$
$=1800.06$
$Q=$ it
$1800.06=1.5\, t$
$t =20 \min$
Answer: 2
Solution
$\left[ Fe \left( H _{2} O \right)_{3} Cl _{3}\right], \underbrace{ K _{3}\left[ Fe ( CN )_{6}\right],\left[ Co \left( NH _{3}\right)_{6}\right] Cl _{3}}_{\text{inner orbital complexes}}$
$K _{3}\left[ Fe ( CN )_{6}\right]$ has more value of $\Delta_{0}$ than that of $\left[ Co \left( NH _{3}\right)_{6}\right] Cl _{3} ;$ as $\overline{ C } N$ is stronger ligand.
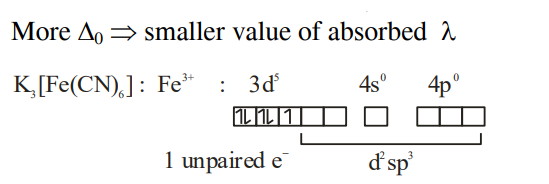
Spin only magnetic moment $(\mu)=\sqrt{3} BM$
$=1.732\, BM$
Rounding off $\Rightarrow 2$
Answer: 9
Solution
Monomer unit of Novolac is

its
molecular mass is $124$ amu. Upon considering molecular weight of polymer as $963$ amu (In question its given as $963$ gram) Now if during formation of Novolac, $(n-1)$ unit of water are removed then
$n \times 124=963+[18 \times( n -1)]$
$n =9$
Answer: 2
Solution
Biuret test is given by all proteins and peptides
having atleast two peptide linkages.
Hence positive test must be given by tripeptide and
Biuret
Answer: 3
Solution

at equivalence point
equivalent of acid $=$ equivalent of base
$0.1 \times 10 \times n =30 \times 0.05 \times 2$
$n =3$
JEE Main Mathematics Question Paper with Solution 2023 June 25th Shift 2 - Evening
A
$A - B =(-1,1)$
B
$B - A = R -(-3,1)$
C
$A \cap B =(-3,-1]$
D
$A \cup B = R -[1,3)$
Solution
$A : x \in(-3,1) B : x \in(-\infty,-1] \cup[3, \infty)$
$B - A =(-\infty,-3] \cup[3, \infty)= R -(-3,3)$
A
37
B
58
C
68
D
92
Solution
$ax ^{2}-2 bx +15=0$
$2 \alpha=\frac{2 b }{ a }, \alpha^{2}=\frac{15}{ a }$
$\frac{\alpha}{2}=\frac{15}{2 b }$
$\alpha=\frac{15}{ b }$
$x ^{2}-2 bx +21=0$
$\left(\frac{15}{ b }\right)^{2}-2 b \left(\frac{15}{ b }\right)+21=0$
$b ^{2}=25$
$\alpha+\beta=2 b , \alpha \beta=21$
$\alpha^{2}+\beta^{2}=4 b ^{2}-42$
$=58$
A
$\arg z _{2}=\frac{\pi}{4}$
B
$\arg z _{2}=-\frac{3 \pi}{4}$
C
$\arg z _{1}=\frac{\pi}{4}$
D
$\arg z _{1}=-\frac{3 \pi}{4}$
Solution
$\overline{ Z }_{1}= i \overline{ Z }_{2}$
$z _{1}=- iz _{2}$
$\arg \left(\frac{ Z _{1}}{ Z _{2}}\right)=\pi$
$\arg \left(- i \frac{ Z _{2}}{\overline{ Z }_{2}}\right)=\pi$
$\arg \left( z _{2}\right)=\theta$
$-\frac{\pi}{2}+\theta+\theta=\pi$
$2 \theta=\frac{3 \pi}{2}$
$\arg \left(z_{2}\right)=\theta=\frac{3 \pi}{4}, \arg z_{1}=\frac{\pi}{4}$
A
$R$
B
$R -\{-11,13\}$
C
$R -\{13\}$
D
$R -\{-11,11\}$
Solution
$\Delta=\begin{vmatrix}- k & 3 & -14 \\ -15 & 4 & - k \\ -4 & 1 & 3\end{vmatrix}=121- k ^{2}$
$\Delta \neq 0 $
$k \in R -\{11,-11\} $ (Unique sol.)
If $k =11$
$\Delta_{ z }=\begin{vmatrix}-11 & 3 & 25 \\ -15 & 4 & 3 \\ -4 & 1 & 4\end{vmatrix} \neq 0$
No solution
If $k =-11$
$\Delta_{ z }=\begin{vmatrix}11 & 3 & 25 \\ -15 & 4 & 3 \\ -4 & 1 & 4\end{vmatrix} \neq 0$
A
$\frac{1}{12}$
B
$-\frac{1}{18}$
C
$-\frac{1}{12}$
D
$-\frac{1}{6}$
Solution
$\displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \tan ^{2} x\left[\sqrt{2 \sin ^{2} x+3 \sin x+4}-\sqrt{\sin ^{2} x+6 \sin x+2}\right]=$
$\displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan ^{2} x\left[\sin ^{2} x-3 \sin x+2\right]}{\sqrt{9}+\sqrt{9}}$
$=\displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan ^{2} x(\sin x-1)(\sin x-2)}{6}$
$=\frac{1}{6} \displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \tan ^{2} x(1-\sin x)$
$=\frac{1}{6} \displaystyle\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin ^{2} x(1-\sin x)(1+\sin x)}{(1-\sin x)}=\frac{1}{12}$
A
$\frac{1}{3}$
B
$\frac{1}{6}$
C
$\frac{2}{3}$
D
$\frac{3}{4}$
Solution
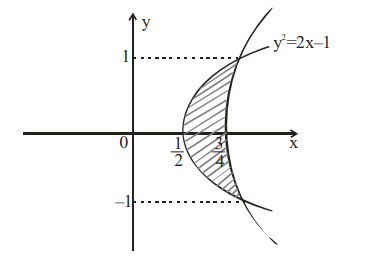
Required area $=2 \int\limits_{0}^{1}\left(\frac{ y ^{2}+3}{4}-\frac{ y ^{2}+1}{2}\right) dy$
$=2 \int\limits_{0}^{1} \frac{1-y^{2}}{4} d y=\frac{1}{2}\left|y-\frac{y^{3}}{3}\right|_{0}^{1}=\frac{1}{3}$
A
${ }^{501} C _{101}(5)^{399}$
B
${ }^{501} C _{101}(5)^{400}$
C
${ }^{501} C _{100}(5)^{400}$
D
${ }^{500} C _{101}(5)^{399}$
Solution
$(5+x)^{500}+x(5+x)^{499}+x^{2}(5+x)^{498}+\ldots .+x^{500}$
$=\frac{(5+x)^{501}-x^{501}}{(5+x)-x}=\frac{(5+x)^{501}-x^{501}}{5}$
$\Rightarrow$ coefficient $x^{101}$ in given expression
$=\frac{{ }^{501} C_{101} 5^{400}}{5}={ }^{501} C_{101} 5^{399}$
A
$\frac{2 \cdot 3^{12}+10}{4}$
B
$\frac{19 \cdot 3^{10}+1}{4}$
C
$5 \cdot 3^{10}-2$
D
$\frac{9 \cdot 3^{10}+1}{2}$
Solution
$S =1 \cdot 3^{0}+2 \cdot 3^{1}+3 \cdot 3^{2}+\ldots \ldots+10.3^{9}$
$3 S =1 \cdot 3^{1}+2.3^{2} \ldots \ldots \ldots \ldots \ldots \ldots \ldots+9 \times 3^{9}+10 \times 3^{10}$
$-2 S =\left(1 \cdot 3^{0}+3^{1}+3^{2} \ldots .3^{9}\right)-10.3^{10}$
$S =5 \times 3^{10}-\left(\frac{3^{10}-1}{4}\right)$
$S =\frac{20.3^{10}-3^{10}+1}{4}=\frac{19.3^{10}+1}{4}$
A
$X$ and $X + Y$ are on the same side of $P$
B
$Y$ and $Y - X$ are on the opposite sides of $P$
C
$X$ and $Y$ are on the opposite sides of $P$
D
$X + Y$ and $X - Y$ are on the same side of $P$
Solution
$P _{1}+\lambda P _{2}=0 $
$\Rightarrow( x +3 y - z -5)+\lambda(2 x - y + z -3)=0$
$(2,1,-2)$ lies on this plane
$\therefore \lambda=1 $
$\Rightarrow $ plane is $ 3 x +2 y -8=0$
A
$y=\sqrt{2} x$
B
$x=\sqrt{2} y$
C
$y^{2}-x^{2}=2 x y$
D
$x^{2}-y^{2}=2 x y$
Solution
Let $(h, k)$ is centre of circle
$\left|\frac{ h - k }{\sqrt{2}}\right|=| h |$
$ k ^{2}- h ^{2}+2 hk =0$
$\therefore$ Equation of locus is $y ^{2}- x ^{2}+2 xy =0$
A
$5$
B
$\frac{\sqrt{21}}{5}$
C
$\frac{\sqrt{26}}{5}$
D
$\frac{\sqrt{26}}{10}$
Solution
From figure $\frac{ r }{ h }=\frac{7}{35}$
$\Rightarrow h =5 r$

Given $\frac{ dV }{ dt }=1$
$\Rightarrow \frac{ d }{ dt }\left(\frac{\pi r ^{2} h }{3}\right)=1$
$\Rightarrow \frac{ d }{ dt }\left(\frac{5 \pi}{3} r ^{3}\right)=1$
$\Rightarrow r ^{2} \frac{ dr }{ dt }=\frac{1}{5 \pi}$
Let wet conical surface area $= S$
$=\pi r \ell=\pi r \sqrt{ h ^{2}+ r ^{2}}$
$=\sqrt{26} \pi r ^{2}$
$\Rightarrow \frac{ dS }{ dt }=2 \sqrt{26} \pi r \frac{ dr }{ dt }$
When $h=10$ then $r=2$
$\Rightarrow \frac{d S }{ dt }=\frac{2 \sqrt{26}}{10}$
A
$b_{3}-b_{2}, b_{4}-b_{3}, b_{5}-b_{4}$ are in an A.P. with common difference $-2$
B
$\frac{1}{ b _{3}- b _{2}}, \frac{1}{ b _{4}- b _{3}}, \frac{1}{ b _{5}- b _{4}}$ are in an A.P. with common difference 2
C
$b_{3}-b_{2}, b_{4}-b_{3}, b_{5}-b_{4}$ are in a G.P.
D
$\frac{1}{ b _{3}- b _{2}}, \frac{1}{ b _{4}- b _{3}}, \frac{1}{ b _{5}- b _{4}}$ are in an A.P. with common difference $-2$
Solution
$b _{ n }=\int\limits_{0}^{\pi / 2} \frac{1+\cos 2 nx }{\sin x } dx$
$b _{ n +1}- b _{ n }=\int\limits_{0}^{\pi / 2} \frac{\cos ^{2}( n +1) x -\cos ^{2} nx }{\sin x } dx$
$=\int\limits_{0}^{\pi / 2} \frac{-\sin (2 n +1) x \sin x }{\sin x } dx$
$=\left(\frac{\cos (2 n +1) x }{2 n +1}\right)_{0}^{\pi / 2}=\frac{-1}{2 n +1}$
$\frac{1}{ b _{3}- b _{2}}, \frac{1}{ b _{4}- b _{3}}, \frac{1}{ b _{5}- b _{4}}$ are in A.P. with c.d. $=-2$
A
$\frac{1}{3}$
B
$\frac{2}{3}$
C
$\frac{3}{2}$
D
$3$
Solution
$\frac{ dy }{ dx }-\frac{ y }{ x }=-\frac{3}{2}\left(\frac{ y }{ x }\right)^{2}$
$y = vx$
$\frac{ dv }{ v ^{2}}=-\frac{3 dx }{2 x }$
$-\frac{1}{ v }=-\frac{3}{2} \ln | x |+ C$
$-\frac{ x }{ y }=\frac{-3}{2} \ln | x |+ C$
$x = e , y =\frac{ e }{3}$
$C =-\frac{3}{2}$
When $x =1, y =\frac{2}{3}$
A
$6(3+2 \sqrt{2})$
B
$3(7+4 \sqrt{3})$
C
$27$
D
$48$
Solution
$\frac{d y}{d x}=\frac{2(1+\sin t) \times \cos t}{1+\cos 2 t}$
$\Rightarrow \frac{2(1+\sin t) \cos t}{2 \cos ^{2} t}=\sqrt{3}$
$\Rightarrow t=\frac{\pi}{6}, y_{0}=27$
A
$\frac{\sqrt{5}(1-\sqrt{3})}{4}$
B
$\frac{1-\sqrt{5}}{8}$
C
$\frac{\sqrt{3}(1-\sqrt{5})}{2}$
D
$\frac{\sqrt{3}(1-\sqrt{5})}{4}$
Solution
$\sin 12^{\circ}+\sin 12^{\circ}-\sin 72^{\circ}$
$=\sin 12^{\circ}-2 \cos 42^{\circ} \sin 30^{\circ}$
$=\sin 12^{\circ}-\sin 48^{\circ}$
$=-2 \cos 30^{\circ} \sin 18^{\circ}$
$=-2 \times \frac{\sqrt{3}}{2} \times \frac{\sqrt{5}-1}{4}$
$=\frac{\sqrt{3}}{4}(1-\sqrt{5})$
A
$\frac{7}{2^{11}}$
B
$\frac{7}{2^{12}}$
C
$\frac{3}{2^{10}}$
D
$\frac{13}{2^{12}}$
Solution
$P ( n )=\frac{1}{ n }$
$P (2)=\frac{1}{2}\,\, P (8)=\frac{1}{8}$
$P (4)=\frac{1}{4}\,\, P (16)=\frac{1}{16}$
$P (32)=\frac{2}{32}$
Possible cases
$16,16,16$ and $32,8,8$
Probability $=\frac{1}{16^{3}}+\frac{2}{32} \times \frac{1}{8} \times \frac{1}{8} \times 3=\frac{13}{16^{3}}$
A
$p \Rightarrow q$
B
$q \Rightarrow p$
C
$\sim(p \Rightarrow q)$
D
$\sim( q \Rightarrow p )$
Solution
$\sim p \vee q \equiv p \rightarrow q$
$\sim q \wedge p \equiv \sim( p \rightarrow q )$
Negation of $\sim( p \rightarrow q ) \rightarrow( p \rightarrow q )$
is $\sim( p \rightarrow q ) \wedge(\sim( p \rightarrow q ))$ i.e. $\sim( p \rightarrow q )$
A
$\frac{3}{2}$
B
$\frac{26}{9}$
C
$\frac{5}{2}$
D
$\frac{23}{6}$
Solution
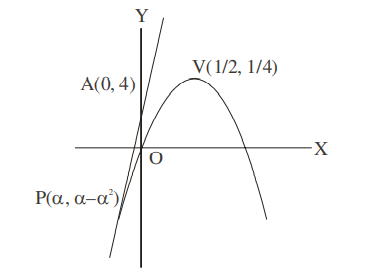
Slope of tangent at $P =$ Slope of line $AP$
$\left. y ^{\prime}\right|_{ P }=1-2 \alpha=\frac{\alpha-\alpha^{2}-4}{\alpha}$
Solving $\alpha=-2 \Rightarrow P(-2,-6)$
Slope of $PV =\frac{5}{2}$
A
$-\frac{\pi}{4}$
B
$-\frac{\pi}{8}$
C
$-\frac{5 \pi}{12}$
D
$-\frac{4 \pi}{9}$
Solution
$\tan ^{-1}\left[\frac{\cos \left(4 \pi-\frac{\pi}{4}\right)-1}{\sin \frac{\pi}{4}}\right]$
$\Rightarrow \tan ^{-1}\left(\frac{\cos \frac{\pi}{4}-1}{\sin \frac{\pi}{4}}\right)$
$\tan ^{-1}\left(\frac{1-\sqrt{2}}{1}\right)=-\frac{\pi}{8}$
A
20
B
12
C
11
D
8
Solution
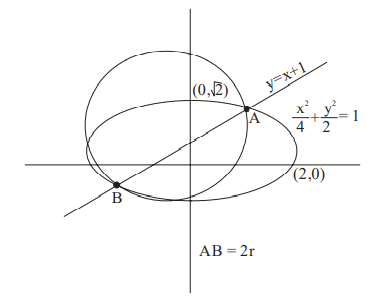
Ellipse $x^{2}+2 y^{2}=4$
Line $y=x+1$
Point of intersection
$x^{2}+2(x+1)^{2}=4$
$3 x^{2}+4 x-2=0$
$\left|x_{1}-x_{2}\right|=\frac{\sqrt{40}}{3}$
$A B=2 r=\left|x_{1}-x_{2}\right| \sqrt{1+m^{2}}$
$m$ is slope of given line
$AB =\frac{\sqrt{40}}{3} \sqrt{1+1}$
$2 r=\frac{\sqrt{80}}{3}$
$\Rightarrow r=\frac{\sqrt{80}}{6}$
$(3 r)^{2}=\left(3 \times \frac{\sqrt{80}}{6}\right)^{2}$
$=\frac{80}{4}=20$
Answer: 1
Solution
$A^{2}=A$ and $B^{2}=B$
Therefore equation $nA ^{ n }+ mB ^{ m }= I$ becomes $nA + mB = I$, which gives $m = n =1$
Only one set possible
Answer: 62
Solution
$f ( g ( x ))=\left[2 g ^{2}( x )\right]+1$
$=\begin{cases} {\left[2(2 x -3)^{2}\right]+1 ; x < 0} \\ {\left[2(2 x +3)^{2}\right]+1 ; x \geq 0} \end{cases}$
$\therefore$ fog is discontinuous whenever $2(2 x-3)^{2}$ or $2(2 x+3)^{2}$ belongs to integer except $x=0$.
$\therefore 62$ points of discontinuity.
Answer: 6
Solution
$\frac{12}{3}\left[\int_{3}^{b}\left(\frac{1}{x^{2}-4}-\frac{1}{x^{2}-1}\right) d x\right]=\log \frac{49}{40}$
$\frac{12}{3} \cdot\left[\frac{1}{4} \ln \left|\frac{x-2}{x+2}\right|-\frac{1}{2} \ln \left|\frac{x-1}{x+1}\right|\right]_{3}^{b}=\log \frac{49}{40}$
$\ln \frac{(b-2)(b+1)^{2}}{(b+2)(b-1)^{2}}=\ln \frac{49}{50}$
$b=6$
Answer: 83
Solution
$T _{ r +1}={ }^{10} C _{ r }\left(2 x ^{3}\right)^{10- r }\left(\frac{3}{ x }\right)^{ r }$
$={ }^{10} C _{ r } 2^{10- r } 3^{ r } x ^{30-4 r }$
Put $r=0,1,2, \ldots .7$ and we get $\beta=83$
Answer: 21
Solution
Mcan deviation about mean of first $n$ natural
numbers is $\frac{ n ^{2}-1}{4 n }$
$\therefore n =21$
Answer: 14
Solution
$(\vec{a} \times \vec{b}) \cdot \vec{b}=0$
$\Rightarrow 13-1-4 \lambda=0$
$\Rightarrow \lambda=3$
$\Rightarrow \vec{b}=\hat{i}+\hat{j}+3 \hat{k}$
$\Rightarrow \vec{a} \times \vec{b}=13 \hat{i}-\hat{j}-4 \hat{k}$
$\Rightarrow(\vec{a} \times \vec{b}) \times \vec{b}=(13 \hat{i}-\hat{j}-4 \hat{k}) \times(\hat{i}+\hat{j}+3 \hat{k})$
$\Rightarrow-21 \vec{b}-11 \vec{a}=\hat{i}-43 \hat{ j }+14 \hat{k}$
$\Rightarrow \vec{a}=-2 \hat{i}+2 \hat{j}-7 \hat{k}$
Now $(\vec{ b }-\vec{ a }) \cdot(\hat{ k }-\hat{ j })+(\vec{ b }+\vec{ a }) \cdot(\hat{ i }-\hat{ k })=14$
Answer: 243
Solution
If $0$ taken twice then ways $=9$
If $0$ taken once then ${ }^{9} C _{1} \times 2=18$
If $0$ not taken then ${ }^{9} C _{1}{ }^{8} C _{1} \cdot 3=216$
Total $=243$
Answer: 3
Solution
$f(x)=\begin{cases}\left(x^{2}-1\right)(x-3)+(x-3), x \in(0,1] \cup[3,4) \\-\left(x^{2}-1\right)(x-3)+(x-3), x \in[1,3]\end{cases}$
$\Rightarrow f^{\prime}(x)=\begin{cases}3 x^{2}-6 x, x \in(0,1) \cup(3,4) \\-3 x^{2}+6 x+2, x \in(1,3)\end{cases}$
$f ( x )$ is non-derivable at $x =1$ and $x =3$
also $f^{\prime}(x)=0$ at $x=1+\sqrt{\frac{5}{3}}$
$\Rightarrow m+M=3$
Answer: 85
Solution
$e ^{2}=1+\frac{ b ^{2}}{ a ^{2}}=\frac{25}{16}$
$\Rightarrow \frac{ b ^{2}}{ a ^{2}}=\frac{9}{16}$ ...(1)
$A \left(\frac{8}{\sqrt{5}}, \frac{12}{5}\right)$ satisfies $\frac{ x ^{2}}{ a ^{2}}-\frac{ y ^{2}}{ b ^{2}}=1$
$\Rightarrow \frac{64}{5 a^{2}}-\frac{144}{25 b^{2}}=1$ ...(2)
Solving (1) & (2) $b =\frac{6}{5} a =\frac{8}{5}$
Normal at $A$ is $\frac{\sqrt{5} a^{2} x}{8}+\frac{5 b^{2} y}{12}=a^{2}+b^{2}$
Comparing it $8 \sqrt{5} x+\beta y=\lambda$
Gives $\lambda=100, \beta=15$
$\lambda-\beta=85$
Answer: 51