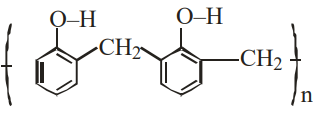
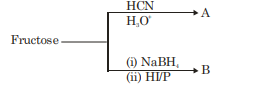
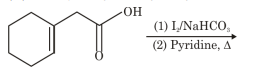
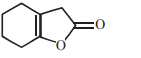
JEE Main Physics Question Paper with Solution 2022 July 28th Shift 2 - Evening
A
Dimensions of $\beta$ is same as that of force.
B
Dimensions of $\alpha^{-1} x$ is same as that of energy.
C
Dimensions of $\eta^{-1} \sin \theta$ is same as that of $\alpha \beta$
D
Dimensions of $\alpha$ is same as that of $\beta$
Solution
$ {[\alpha \beta]=[\eta]=[\sin \theta]=\text { Dimensionless }} $
$ [\eta^{-1} \sin \theta]=[\alpha \beta]=\text { D.L. }$
A
$-30 \hat{y}$
B
$30 \hat{y}$
C
$3 \hat{x}+15 \hat{y}$
D
$3 \hat{ x }+15 \hat{ y }+7 \hat{ z }$
Solution
$\overrightarrow{ r }=3 \hat{ t }+5 t ^3 \hat{ j }+7 k$
$ \frac{ d ^2 \overrightarrow{ r }}{ dt ^2}=30 t \hat{ j }$
At $t =1 \Rightarrow \frac{ d ^2 \overrightarrow{ r }}{ dt ^2}=30 \hat{ j }$
A
$300 \, N$
B
$500\, N$
C
$250\, N$
D
$400\, N$
Solution
$F =\rho a v^2=10^3 \times 10 \times 10^{-4} \times 20 \times 20$
$F =400$
A
6
B
2
C
1.5
D
4
Solution

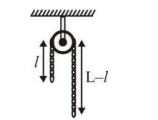
$a =\frac{\left( m _2- m _1\right)}{\left( m _2+ m _1\right)} g $
$ \frac{ g }{2}=\frac{(\lambda( L -\ell)-\lambda \ell) g }{\lambda L } $
$\Rightarrow L =\frac{ L }{4}=\frac{ L }{ x } $
$ x =4$
A
$45 \,m$
B
$90 \,m$
C
$125\,m$
D
$25\, m$
Solution
Using $mv =\sqrt{2 mk }$
$ u =\frac{1}{0.2} \sqrt{2 \times 0.2 \times 90}=30 \,m / s $
$ v =\frac{1}{0.2} \sqrt{2 \times 0.2 \times 40}=20 \, m / s$
$ a =\frac{20-30}{1}=-10 \, m / s ^2 $
$ s =\frac{- u ^2}{2 a }=45 \,m$
A
$1200 \, km$
B
$1600 \, km$
C
$3200 \, km$
D
$4800\, km$
Solution
$t \propto \frac{1}{\sqrt{g}} \text { and } g \propto \frac{1}{( R + h )^2} $
$\frac{t_1}{t_2}=\sqrt{\frac{g^{\prime}}{g}}=\sqrt{\frac{R^2}{(R+h)^2}}$
$\frac{t_1}{t_2}=\frac{4}{6}=\frac{R}{(R+h)}$
$ \Rightarrow h=3200\, km $
A
$11.6 \,m / s$
B
$10.8\, m / s$
C
$17.8 \,m / s$
D
$14.4 \,m / s$
Solution
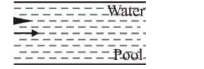
Apply Bernoulli's theorem between Piston and hole
$P _{ A }+\rho gh = P _0+\frac{1}{2} \rho v_{ e }^2$
Assuming there is no atmospheric pressure on piston
$ \frac{5 \times 10^5}{\pi}+10^3 \times 10 \times 10=1.01 \times 10^5+\frac{1}{2} \times 10^3 \times v _{ e }^2$
$ v _{ e }=17.8 \,m / s$
A
$2229 J$
B
$5616 J$
C
$9360 J$
D
$13,104 J$
Solution
$ v _{ rms } \propto \sqrt{ T } $
$ v _{ rms } \propto \sqrt{300 K }, v _{ rms _{ f }}=2 v _{ rms _{ i }}$
$ v _{ rms _{ f }} \propto \sqrt{1200 K } $
$ T _{ f }=1200 K , T _{ i }=300 K , n =\frac{14}{28}=\frac{1}{2}$
$ Q = nC _{ v } \Delta T =\frac{1}{2} \times \frac{5 R }{2} \times 900 $
$ Q =9360\, J $
A
$\frac{4 KC _0}{3+ K }$
B
$\frac{3 KC _0}{3+ K }$
C
$\frac{3+ K }{4 KC _0}$
D
$\frac{ K }{4+ K }$
Solution

$ x+y+\frac{3 d}{4}=d $
$ x + y =\frac{ d }{4} $
$ \frac{ A \in_0}{ d }= C _0 $
$ \Delta V = Ex +\frac{ E }{ k } \times \frac{3 d }{4}+ Ey $
$ =\frac{3 Ed }{4 k }+ E ( x + y )$
$ \Delta V = E \left[\frac{3 d }{4 k }+\frac{ d }{4}\right]$
$ \Delta V =\frac{\sigma}{\epsilon_0}\left[\frac{3 d + dk }{4 k }\right]=\frac{ Qd }{ A \in_0}\left[\frac{3+ k }{4 k }\right]$
$ \frac{ Q }{\Delta V }= C =\frac{ A \in_0}{ d }\left[\frac{4 k }{3+ k }\right]=\frac{4 kC _0}{ k +3}$
A
$\tan ^{-1}$ (4)
B
$\tan ^{-1}$ (2)
C
$\tan ^{-1}\left(\frac{1}{3}\right)$
D
$\tan ^{-1}$ (3)
Solution

$ a _{ y }=\frac{ F _{ y }}{ m }=\frac{ e ( E )}{ m }=\frac{ e \left(\frac{8 m }{ e }\right)}{ m }=8 m / s ^2 $
$ s _{ x }= u _{ x } t $
$1=2 \times t $
$ t =\frac{1}{2} \sec $
$ v _{ y }= u _{ y }+ a _{ y } t $
$ v _{ y }=0+8 \times \frac{1}{2} $
$ v _{ y }=4 m / s $
$ \tan \theta=\frac{ v _y}{ v _{ x }}=\frac{4}{2}=2 $
$\Rightarrow \theta=\tan ^{-1}(2)$
A
Both statement I and statement II are correct
B
Both statement I and statement II are incorrect
C
Statement I is correct but statement II is incorrect
D
Statement I is incorrect but statement II is correct.
Solution
Statement $1- R =80 \Omega$
$R _1= R _2= R _3= R _4=20 \Omega$
In parallel $R _{ eq }=\frac{20}{4}=5 \Omega$
Statement 2 -
$R _1=3 R$

$P_{t h}=\frac{v^2}{R}$
$\frac{P_1}{P_2}=\left(\frac{R_2}{R_1}\right)=\frac{2}{3}$ (where $P$ is power)
A
$0.126\, N$
B
$0.312\, N$
C
$0.216 \,N$
D
$0.245\, N$
Solution
$ F _{ M }( CD )= BI \ell_{ eff } $
$ =0.5 \times(10) \times\left(5 \sin 60 \times 10^{-2}\right) $
$ =0.216\, N $
A
$9: 4$
B
$12: \sqrt{5}$
C
$8: 1$
D
$5: \sqrt{3}$
Solution

$ B _1=\frac{\mu_0 I }{2 R } $
$B _2=\frac{\mu_0 IR ^2}{2\left( R ^2+3 R ^2\right)^{3 / 2}}=\frac{1}{8}\left(\frac{\mu_0 I }{2 R }\right)=\frac{ B _1}{8} $
$ \frac{ B _1}{ B _2}=\frac{8}{1}$
A
$800\, \Omega$ and $1.06 \,\Omega$
B
$10 \,\Omega$ and $500\, \Omega$
C
$800\, \Omega$ and $0.32\, \Omega$
D
$1.06\, \Omega$ and $500\, \Omega$
Solution
$ \frac{\left(8 \times 10^3\right)^2}{R_P}=80 \times 10^3 $
$ R_P=800\, \Omega$
$\frac{(160)^2}{R_S}=80 \times 10^3$
$ R_S=0.32\, \Omega$
A
$25.92 \times 10^2 \, W / cm ^2$
B
$8.64 \times 10^{-6} \, W / cm ^2$
C
$6.0 \, W / cm ^2$
D
$0.06 \, W / cm ^2$
Solution
$ \frac{ I }{ C } \times \text { area }=\text { force }$
$ \frac{ I }{ C } \times 36 \times 10^{-4}=7.2 \times 10^{-9} $
$ I =\frac{7.2 \times 10^{-9} \times 3 \times 10^8}{36 \times 10^{-9} \times 10} $
$ =\frac{6 \times 10^{-1}}{10^{-3}} $
$ I =6 \times 10^2 \frac{ w }{ m ^2} $
$ =0.06 \frac{ w }{ cm ^2}$
A
$1.0$
B
$\frac{9}{7}$
C
$\frac{3}{2}$
D
$\frac{4}{3}$
Solution
$P =\frac{\mu_2}{ f }=\left(\mu_1-\mu_2\right)\left(\frac{1}{ R _1}-\frac{1}{ R _2}\right)$
(For this formula refer to NCERT Part-2, Chapter-9, Page no. 328, solved example 8) $\left(\mu_1\right.$ is refractive index of lens and $\mu_2$ is of surrounding medium)
$ 1.25=\left(1.5-\mu_2\right)\left(\frac{1}{0.2}+\frac{1}{0.4}\right) $
$ \frac{1.25 \times 0.08}{0.6}=\left(1.5-\mu_2\right) $
$\Rightarrow \mu_2=\frac{4}{3}$
A
$1: 2$
B
$1: 3$
C
$2: 3$
D
$3: 2$
Solution
$ \frac{1}{2} mv _1^2=4 \phi $
$ \frac{1}{2} mv _2^2=9 \phi$
$ \frac{ v _1}{ v _2}=\frac{2}{3}$
A
$5 \min$
B
$7.5 \min$
C
$15 \min$
D
$30 \min$
Solution
Remaining $=\frac{1}{8} $
$3 t _{1 / 2}=15 \min $
$ t _{1 / / 2}=5 \min $
A
$0.1 \,V$
B
$1.0\, V$
C
$10 \,V$
D
$100\, V$
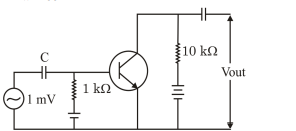
Solution
$ \frac{v_{\text {out }}}{ v _{\text {in }}}=\beta \frac{ R _{\text {out }}}{ R _{\text {in }}} $
$ v _{\text {out }}=\frac{100 \times 10 \times 10^3}{10^3} \times 10^{-3}$
$ =1\, V $
A
$220 \,kHz$
B
$180 \,kHz$
C
$360\, kHz$
D
$440\, kHz$
Solution
Given
FM broadcast
Modulating frequency $=20\, k \,Hz = f$
Deviation ratio $=\frac{\text { frequency deviation }}{\text { modulating frequency }}=\frac{\Delta f }{ f }$
$\Rightarrow$ frequency deviation $-\Delta f = f \times 10$
$=20\, kHz \times 10=200\, kHz$
$\Rightarrow$ Bandwidth $=2( f +\Delta f )$
$=2(20+200) \,kHz$
$=440 \,kHz$
Answer: 392
Solution
$t _{ a }=\frac{ u }{ g }=\frac{19.6}{9.8}=2\, s$
$ t _{ d }=6-2 s =\sqrt{\frac{2 h _{\max }}{ g }}$
$ \Rightarrow h _{\max }=\frac{16 \times 9.8}{2}=\frac{392}{5}$
Answer: 8
Solution

$dm =\lambda \cdot dx =\lambda_0\left(1-\frac{ x ^2}{\ell^2}\right)$
$ X _{ cm }=\frac{\int xdm }{\int dm _{\ell}}$
$=\frac{\lambda_0 \int\limits_0^{\ell}\left( x -\frac{ x ^3}{\ell^2}\right) dx }{\ell}=\frac{\frac{\ell^2}{2}-\frac{\ell^4}{4 \ell^2}}{\int\limits_0^{\ell} \lambda_0\left(1-\frac{ x ^2}{\ell^2}\right) dx }=\frac{3 \ell}{8}$
Answer: 30
Solution

$ =\frac{ mg +\frac{ mv ^2}{ R }}{ AY }$
$=\frac{20+\frac{2(5)^2}{0.5}}{3 \times 10^{-6} \times 10^{11}}=30 \times 10^{-5}$
Answer: 750
Solution
$ W = nR \Delta T =150 J$
$ Q =\left(\frac{ f }{2}+1\right) nR \Delta T =\left(\frac{8}{2}+1\right) 150=750 J $
Answer: 2
Solution
$U =4(1-\cos 4 x ) $
$ F =-\frac{ dU }{ dx }=-4(+\sin 4 x ) 4=-16 \sin (4 x ) $
$ \text { For small } \theta$
$ \sin \theta \approx \theta $
$ F =-64 x $
$ a =-64 x / m =-16 x$
$ \omega^2=16$
$ T =\frac{2 \pi}{\omega}=\frac{\pi}{2}$
Answer: 14
Solution
$ R _1=\frac{ V ^2}{ P }=\frac{220^2}{100}=484$
$R _2=\frac{ V ^2}{ P }=\frac{220^2}{60}=484\left(\frac{10}{6}\right) $
$ I =\frac{220}{484+484 \times \frac{10}{6}} $
$ P _1= I ^2 R _1=14.06 \,W $
Answer: 1
Solution
Just after closing the switch S, inductor behaves like an open circuit.
$I=\frac{6}{2+4}=1 \,A$
Answer: 400
Solution
After $10 \sec$.
$u =-80 \,cm$
$f =-100 \,cm$
$\frac{1}{ v }+\frac{1}{ u }=\frac{1}{ f }$
$v =400\, cm$
Answer: 15
Solution
$ v u=f^2 $ (by Newton's formula)
$ f^2=225 $
$ f=15\, cm $
Answer: 5
Solution
$ T =2 \pi \sqrt{\frac{\ell}{ g }} $
$ g =\frac{1}{4 \pi^2} \frac{ T ^2}{\ell} $
$ \frac{\Delta g }{ g }=\frac{2 \Delta T }{ T }+\frac{\Delta \ell}{\ell}$
$ \frac{\Delta g }{ g }=2 \cdot \frac{1}{100 \times 0.5}+\frac{1 mm }{10 cm }$
$ \frac{\Delta g }{ g }=\frac{5}{100}$
JEE Main Chemistry Question Paper with Solution 2022 July 28th Shift 2 - Evening
A
Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
B
Both $A$ and $R$ are true but $R$ is NOT the correct explanation of $A$
C
$A$ is true but $R$ is false
D
$A$ is false but $R$ is true

A
$Na > Mg > Be > Si > P$
B
P $>$ Si $> Be > Mg > Na$
C
$Si > P > Be > Na > Mg$
D
$Be > Na > Mg > Si > P$
Solution
Across a period metallic character decreases
A
Both $A$ and $R$ are correct and $R$ is the correct explanation of $A$
B
Both $A$ and $R$ are correct but $R$ is NOT the correct explanation of $A$
C
$A$ is correct but $R$ is not correct
D
$A$ is not correct but $R$ is correct
Solution
$\Delta G =\Delta H - T \Delta S$
$\because$ Entropy of liquid is more than solid
$\therefore$ on melting the entropy increases and $\Delta G$ becomes more negative and hence it becomes easier to reduce metal
A
$CaCO _3$ and $MgCO _3$
B
$Ca ( OH )_2$ and $Mg ( OH )_2$
C
$CaCO _3$ and $Mg ( OH )_2$
D
$Ca ( OH )_2$ and $MgCO _3$
Solution
Sol. In Clark's method lime water is used
$Ca \left( HCO _3\right)_2+2 Ca ( OH )_2 \rightarrow 2 CaCO _3+2 H _2 O $
$ Mg \left( HCO _3\right)_2+2 Ca ( OH )_2 \rightarrow 2 CaCO _3+ Mg ( OH )_2+2 H _2 O$
A
Both Statement I and Statement II are true
B
Both Statement I and Statement II are false
C
Statement $I$ is true but Statement $Il$ is false
D
Statement I is false but Statement II is true
Solution
Alloy of $Li$ and $Mg$ is used to make armour plates and not aircraft plates. Calcium plays important roles in neuromuscular function, interneuronal transmission and cell membrane integrity
A
$PCl _5, SO _2$ and $S _2 Cl _2$
B
$PCl _3 . SO _2$ and $S _2 Cl _2$
C
$PCl _3, SO _2$ and $Cl _2$
D
$PCl _5, SO _2$ and $Cl _2$
Solution
$P _4+8 SOCl _2 \rightarrow 4 PCl _3+4 SO _2+2 S _2 Cl _2$
A
$HI , NO _2$ and $H _2 O$
B
$HIO _2, N _2 O$ and $H _2 O$
C
$HIO _3, NO _2$ and $H _2 O$
D
$HIO _4, N _2 O$ and $H _2 O$
Solution
$I _2+10 HNO _{3(\text { oonc })} \Rightarrow 2 HIO _3+10 NO _2+4 H _2 O$
A
$Sm ^{2+}$ and $Er ^{3+}$
B
$Yb ^{2+}$ and $Lu ^{3+}$
C
$Eu ^{2+}$ and $Tb ^{4+}$
D
$Tb ^{2+}$ and $Tm ^{4+}$

A
Both A and R are true and R is the correct explanation of A
B
Both A and R are true but R is NOT the correct explanation of A
C
A is true but R is false
D
A is false but R is true
Solution
$2 KMnO _4+16 HCl \rightarrow 2 MnCl _2+2 KCl +8 H _2 O + Cl _2$
$HCl$ gets oxidised by $KMnO _4$ into $Cl _2$
A
A-IV, B-I, C-III, D-II
B
A-I. B-IV, C-III, D-II
C
A-I. B-IV, C-II, D-III
D
A-IV, B-I, C-II. D-III
Solution
$Ni ( CO )_4$ Hybridisation $sp ^3$
$\left[ Ni ( CN )_4\right]^{2-}$ Hybridisation $dsp ^2$
$\left[ Co ( CN )_6\right]^{3-}$ Hybridisation $d ^2 sp ^3$
$\left[ Co ( F )_6\right]^{3-}$ Hybridisation $sp ^3 d ^2$
A
$N _2$ is unreactive in the condition of atmosphere.
B
Oxides of nitrogen are unstable.
C
Reaction between them can occur in the presence of a catalyst.
D
The reaction is endothermic and require very high temperature.
Solution
$N _2+ O _2 \xrightleftharpoons{(1483-2000 K )}2 NO$
(Endothermic and feasible at high temperature)
A
C < D < E < A < B
B
D < B < E < A < C
C
D < C < E < A < B
D
C < D < E < B < A
Solution
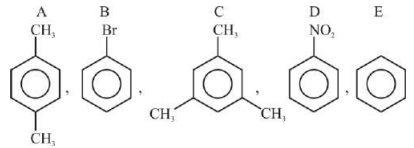
$- NO _2$ is strongly deactivating
$- Br$ - deactivating
$- CH _3$-activating group
$D < B < E < A < C$
A
Both A and R are true and R is the correct explanation of A
B
Both A and R are true but R is NOT the correct explanation of A
C
A is true but R is false
D
A is false but R is true
Solution

Due to formation of anilinium ion in acidic medium meta product is also obtained in significant amount
A
A-II, B-III, C-IV, D-I
B
A-III, B-II, C-IV, D-I
C
A-III, B-I, C-IV, D-II
D
A-I. B-III, C-IV, D-II
Solution
Neoprene is elastomer
Nylon-6, 6 is fiber
PVC is thermoplastic
Novolac is thermosetting
A
Both Statement I and Statement II are true
B
Both Statement I and Statement II are false
C
Statement I is true but Statement II is false
D
Statement I is false but Statement II is true
Solution
Some drugs do not bind to active sites. These bind to different site of enzyme called allosteric sites.
A
Both A and R are true and R is the correct explanation of A
B
Both A and R are true but R is NOT the correct explanation of A
C
A is true but R is false
D
A is false but R is true
Solution
Theory based
Thin layer chromoatography (TLC) is another
type of adsorption chromatography, which
involve sepration of substance of a mixture
ovel a thin layer of an adsorbent coated on
glass plate.
A thin layer (about $0.2$ mm thick) of an
adsorbent (silica gel) or (Alumina) in spread
overa glass plate of suitable size. Hence
Assertion (A) is correct and Reason (R) is
correct explanation of (A)
A
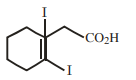
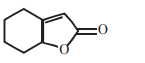
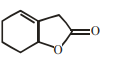
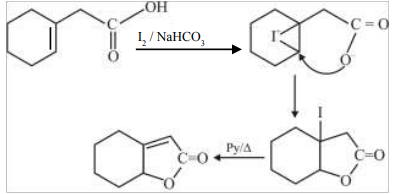
$A = C _7 H _{14} O _8, B = C _6 H _{14}$
B
$A = C _7 H _{13} O _7, B = C _7 H _{14} O$
C
$A = C _7 H _{12} O _8, B = C _6 H _{14}$
D
$A = C _7 H _{14} O _8, B = C _6 H _{14} O _6$

Answer: 87
Solution
$ a =4 \times 10^{-8} cm $
$ d =9.03 \,g / ml $
$ d =\frac{ ZM }{ N _{ A } a ^3}$
$ M =\frac{9.03 \times 6.02 \times 10^{23} \times 64 \times 10^{-24}}{4}=86.97$
Answer: 2
Solution
$ \lambda=\frac{ h }{\sqrt{2 mK }} $
$K =\frac{ h ^2}{2 m \lambda^2} $
$K =\frac{ h ^2}{2 m \lambda^2}=\frac{43.9 \times 10^{-68}}{2 \times 9.1 \times 10^{-31} \times 10.89 \times 10^{-20}}$
$ K =2.215 \times 10^{-18} $
$ E _{ abs }= E _{\text {req }}+ K $
$ \frac{ E _{\text {abs }}}{ E _{\text {req }}}=1+\frac{ K }{ E _{\text {req }}}=1+\frac{2.215 \times 10^{-18}}{13.6 \times 1.602 \times 10^{-19}}=2.0166$
Answer: 2
Solution
$ Y _{ A }=0.5 \Rightarrow Y_B=0.5$
$P _{ A }= P _{ B }=0.4 \,atm $
$ P _{ A }= P _{ A }^0 X _{ A } $
$ P _{ A }^0=2$
Answer: 2
Solution

$K _{ p }=\frac{\left(\frac{0.8}{2.6}\right)^2}{\left(\frac{1.2}{2.6}\right)^2\left(\frac{0.6}{2.6}\right)}=1.925$
Answer: 22
Solution
$ V =22.78\, ml , T =280\, K $
$ P _{\text {total }}=759\, mm\, Hg$
$ P _{ N _2}=759-14.2=744.8 \, mm\, Hg $
$ n _{ N _2}=\frac{744.8 \times 22.78}{760 \times 1000 \times 0.082 \times 280}=0.00097$
$ W _{\text {Nitrogen }}=0.02716$
$\% N =\frac{0.02716}{0.125} \times 1000=21.728$
Answer: 5
Solution
$IO _4^{-}+ H _2 O _2 \rightarrow IO _3^{-}+ O _2$
Answer: 8
Solution
$ K = Ae ^{- Ea / RT } $
$ \ln k =\frac{- Ea }{ RT }+\ln A $
$ \text { Slope }=\frac{ Ea }{ R }=\frac{20}{5} $
$E _{ a }=4 R =8\, Cal / mol $
Answer: 3
Solution
$ \frac{ X }{ m }= KP ^{\frac{1}{ n }}$
$ \log \frac{ x }{ m }=\frac{1}{ n } \log p +\log k $

Answer: 3
Solution
Internal energy, volume enthalpy are state variable
JEE Main Mathematics Question Paper with Solution 2022 July 28th Shift 2 - Evening
A
7
B
5
C
4
D
3
Solution
$S \cap T =\{-5,-4,3\}$
A
non-real complex numbers
B
real and both negative
C
real and both positive
D
real and exactly one of them is positive
Solution
$ a=\frac{-1}{\alpha^2}-\frac{1}{\beta^2}-2$
$ b=\frac{1}{\alpha^2}+\frac{1}{\beta^2}+1+\frac{1}{\alpha^2 \beta^2}$
$ a+b=\frac{1}{(\alpha \beta)^2}-1=\frac{1}{6}-1=-\frac{5}{6} $
$x^2-\left(-\frac{5}{6}-2\right) x+\left(2-\frac{5}{6}\right)=0 $
$ 6 x^2+17 x+7=0 $
$ x=-\frac{7}{3}, x=-\frac{1}{2} $ are the roots
Both roots are real and negative.
A
$A ^4- B ^4$ is a symmetric matrix
B
$AB - BA$ is a symmetric matrix
C
$B ^5- A ^5$ is a skew-symmetric matrix
D
$AB + BA$ is a skew-symmetric matrix
Solution
Given that $A ^{ T }=A, B^{ T }=- B$
(A) $C = A ^4- B ^4$
$C^T=\left(A^4-B^4\right)=\left(A^4\right)^T-\left(B^4\right)^T=A^4-B^4=C$
(B) $C = AB - BA$
$ C^T=(A B-B A)^T=(A B)^T-(B A)^T$
$=B^T A^T-A^T B^T=-B A+A B=C$
(C) $C = B ^5- A ^5$
$C^T=\left(B^5-A^5\right)^T=\left(B^5\right)^T-\left(A^5\right)^T=-B^5-A^5$
(D) $C = AB + BA$
$ C^T=(A B+B A)^T=(A B)^T+(B A)^T $
$=-B A-A B=-C$
$\therefore$ Option $C$ is not true.
A
$-4$
B
$\frac{13}{2}$
C
$\frac{23}{2}$
D
4
Solution
$ f (0)+3+\lambda+4=14 $
$ \therefore f (0)=7-\lambda= c $
$ f (1)= a + b + c =3 $.....(i)
$ f (3)=9 a +3 b + c =4 $.....(ii)
$ f (-2)=4 a -2 b + c =\lambda$.....(iii)
(ii) - (iii)$ a + b =\frac{4-\lambda}{5} $ put in equation (ii)
$ \frac{4-\lambda}{5}+7-\lambda=3 $
$6 \lambda=24 ; \lambda=4$
A
$R -\{-1\}$
B
$R -\{-1,1\}$
C
$R -\{1\}$
D
$R-\{0\}$
Solution
Note: $n$ should be given as a natural number.
$f(x=\begin{cases}
\frac{-\sin (x-1)}{x-1} & x< -1 \\
-(\sin 2+1) & x=-1 \\
\cos 2 \pi x & -1< x< 1 \\
1 & x=1 \\
\frac{-\sin (x-1)}{x-1} & x >1
\end{cases}$
$f(x)$ is discontinuous at $x=-1$ and $x=1$
A
increasing in $\left(-\frac{1}{2}, 1\right)$
B
decreasing in $\left(\frac{1}{2}, 2\right)$
C
increasing in $\left(-1,-\frac{1}{2}\right)$
D
decreasing in $\left(-\frac{1}{2}, \frac{1}{2}\right)$
Solution
$ f(x)=x e^{x(1-x)} $
$f^{\prime}(x)=-e^{x(1-x)}(2 x+1)(x-1)$
$f ( x )$ is increasing in $\left(-\frac{1}{2}, 1\right)$
A
0
B
$\tan ^{-1}\left(\frac{1}{\sqrt{2}}\right)-\frac{\pi}{4}$
C
$\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)-\frac{\pi}{4}$
D
$\frac{-\pi}{12}$
Solution
$ f(x)=\tan ^{-1}(\sin x-\cos x)$
$ f^{\prime}(x)=\frac{\cos x+\sin x}{(\sin x-\cos x)^2+1}=0$
$ \therefore x=\frac{3 \pi}{4}$

$\text{sum}=\tan ^{-1} \sqrt{2}-\frac{\pi}{4} $
$ =\cos ^{-1} \frac{1}{\sqrt{3}}-\frac{\pi}{4}$
A
$\frac{-2 \sqrt{2}}{3}$
B
$\frac{2}{3}$
C
$\frac{1}{3}$
D
$\frac{-2}{3}$
Solution
$ x =2 \sqrt{2} \cos t \sqrt{\sin 2 t } $
$ \frac{ dx }{ dt }=\frac{2 \sqrt{2} \cos 3 t }{\sqrt{\sin 2 t}}$
$ y ( t )=2 \sqrt{2} \sin t \sqrt{\sin 2 t } $
$ \frac{ dy }{ dt }=\frac{2 \sqrt{2} \sin 3 t }{\sqrt{\sin 2 t}}$
$ \frac{ dy }{ dx }=\tan 3 t $
$ \frac{ dy }{ dx }=-1 \text { at } t =\frac{\pi}{4}$
$ \frac{d^2 y}{d x^2}=\frac{3}{2 \sqrt{2}} \sec ^3 3 t \cdot \sqrt{\sin 2 t}=-3 \text { at } t=\frac{\pi}{4} $
$ \therefore \frac{1+\left(\frac{d y}{d x}\right)^2}{\frac{d^2 y}{d x^2}}=\frac{1+1}{-3}=-\frac{2}{3}$
A
$50 I _6-9 I _5= xI _5^{\prime}$
B
$50 I _6-11 I _5= xI _5^{\prime}$
C
$50 I _6-9 I _5= I _5^{\prime}$
D
$50 I _6-11 I _5= I _5^{\prime}$
Solution
$I_n(x)=\int\limits_0^{ x } \frac{ dt }{\left( t ^2+5\right)^{ n }}$
Applying integral by parts
$I_n(x)=\left[\frac{t}{\left(t^2+5\right)^n}\right]_0^x-\int\limits_0^x n\left(t^2+5\right)^{-n-1} \cdot 2 t^2$
$I_n(x)=\frac{x}{\left(x^2+5\right)^n}+2 n \int\limits_0^x \frac{t^2}{\left(t^2+5\right)^{n+1}} d t$
$I_n(x)=\frac{x}{\left(x^2+5\right)^n}+2 n \int\limits_0^x \frac{\left(t^2+5\right)-5}{\left(t^2+5\right)^{n+1}} d t$
$I_n(x)=\frac{x}{\left(x^2+5\right)^n}+2 n I_n(x)-10 n I_{n+1}(x)$
$10 n I_{n+1}(x)+(1-2 n) I_n(x)=\frac{x}{\left(x^2+5\right)^n}$
$ P u t n=5$
A
$2+ e -\log _{ e } 2$
B
$1+ e -\log _{ e } 2$
C
$e -\log _{ e } 2$
D
$1+\log _{ e } 2$
Solution

Required area is
$=\int\limits_{ e - e ^2}^0 \ln \left( x + e ^2\right)-1 dx +\int\limits_0^{\ln 2} 2 e ^{- x }-1 dx =1+ e -\ln 2$
A
$11+6 \log _{ e } 3$
B
19
C
$12-2 \log _e 3$
D
$19-6 \log _e 3$
Solution
$ \frac{d y}{d x}+\frac{1}{x^2-1} y=\left(\frac{x-1}{x+1}\right)^{\frac{1}{2}}$
$ \frac{d y}{d x}+P y=Q$
$ \text { I.F. }=e^{\int P d x}=\left(\frac{x-1}{x+1}\right)^{\frac{1}{2}} $
$y\left(\frac{x-1}{x+1}\right)^{\frac{1}{2}}=\int\left(\frac{x-1}{x+1}\right)^1 d x$
$ =x-2 \log _e|x+1|+C$
$ \text { Curve passes through }\left(2, \frac{1}{\sqrt{3}}\right)$
$\Rightarrow C=2 \log _e 3-\frac{5}{3}$
$\text { at } x=8, \sqrt{7} y(8)=19-6 \log _{ e } 3$
A
$2 x y \frac{d y}{d x}+\left(x^2-y^2+4\right)=0$
B
$2 x y \frac{d y}{d x}+\left(x^2+y^2-4\right)=0$
C
$2 x y \frac{d y}{d x}+\left(y^2-x^2+4\right)=0$
D
$2 x y \frac{d y}{d x}-\left(x^2-y^2+4\right)=0$
Solution
Sol. Equation of circle passing through $(0,-2)$ and $(0,2)$ is
$x^2+\left(y^2-4\right)+\lambda x=0,(\lambda \in R)$
Divided by $x$ we get
$\frac{x^2+\left(y^2-4\right)}{x}+\lambda=0$
Differentiating with respect to $x$
$ \frac{x\left[2 x+2 y \cdot \frac{d y}{d x}\right]-\left[x^2+y^2-4\right] \cdot 1}{x^2}=0 $
$ \Rightarrow 2 x y \cdot \frac{d y}{d x}+\left(x^2-y^2+4\right)=0$
A
$\frac{3 \sqrt{3}}{2}$
B
$\frac{3 \sqrt{3}}{4}$
C
$\frac{3}{2 \sqrt{3}}$
D
$\frac{3}{4 \sqrt{3}}$
Solution
Equation of chord $AB : 2 x =3$

$ OA = OB =\sqrt{3} $
$ AM =\frac{\sqrt{3}}{2}$
Area of triangle $OAB =\frac{1}{2}(2 AM )( OM )$
$=\frac{3 \sqrt{3}}{4}$ sq. units
A
$(2 \sqrt{3}, 3 \sqrt{2})$
B
$(3 \sqrt{3},-6 \sqrt{2})$
C
$(\sqrt{3},-\sqrt{6})$
D
$(3 \sqrt{6}, 6 \sqrt{2})$
Solution
$H : \frac{ x ^2}{ a ^2}-\frac{ y ^2}{ b ^2}=1$
Foci : S (ae, 0), S' $(-a e, 0)$
Foot of directrix of parabola is $(-a e, 0)$
Focus of parabola is (ae, 0 )
Now, semi latus rectum of parabola $=\left| SS ^{\prime}\right|=2 ae$
Given, $4 a e=e\left(\frac{2 b^2}{a}\right)$
$\Rightarrow b ^2=2 a ^2$....(1)
Given, $(2 \sqrt{2},-2 \sqrt{2})$ lies on $H$
$\Rightarrow \frac{1}{ a ^2}-\frac{1}{ b ^2}=\frac{1}{8}$...(2)
From (1) and (2)
$ a ^2=4, b ^2=8$
$ \because b ^2= a ^2\left( e ^2-1\right) $
$ \therefore e =\sqrt{3} $
$\Rightarrow \text { Equation of parabola is } y ^2=8 \sqrt{3} x$
A
$(0,-2,-2)$
B
$(-5,0,-1)$
C
$(3,-1,0)$
D
$(0,4,5)$
Solution
Given, $L _1: \frac{ x -1}{\lambda}=\frac{ y -2}{1}=\frac{ z -3}{2}$
and $L_2: \frac{ x +26}{-2}=\frac{ y +18}{3}=\frac{ z +28}{\lambda}$ are coplanar
$\Rightarrow\begin{vmatrix}27 & 20 & 31 \\ \lambda & 1 & 2 \\ -2 & 3 & \lambda\end{vmatrix}=0$
$\Rightarrow \lambda=3$
Now, normal of plane $P$, which contains $L _1$ and $L_2$
$=\begin{vmatrix}\hat{ i } & \hat{ j } & \hat{ k } \\ 3 & 1 & 2 \\ -2 & 3 & 3\end{vmatrix}$
$=-3 \hat{ i }-13 \hat{ j }+11 \hat{ k } $
$ \Rightarrow $Equation of required plane $ P $
$3 x +13 y -11 z +4=0$
$(0,4,5)$ does not lie on plane $P$.
A
$(48,-13)$
B
$(24,-13)$
C
$(48,11)$
D
$(24,-5)$
Solution
Normal of plane $P$ :
$=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\-2 & 1 & -3 \\-1 & 2 & -2\end{vmatrix}=4 \hat{i}-\hat{j}-3 \hat{k}$
Equation of plane $P$ which passes through (2, $2,-2)$ is $4 x-y-3 z-12=0$
Now, A $(3,0,0)$, B $(0,-12,0)$, C $(0,0,-4)$
$ \Rightarrow \alpha=3, \beta=-12, \gamma=-4$
$\Rightarrow p =\alpha+\beta+\gamma=-13$
Now, volume of tetrahedron $OABC$
$ V =\left|\frac{1}{6} \overrightarrow{ OA } \cdot(\overrightarrow{ OB } \times \overrightarrow{ OC })\right|=24$
$( V , p )=(24,-13)$\
A
$\left(-\infty,-\frac{4}{3}\right)$
B
$\Phi$
C
$\left(-\frac{4}{3}, 0\right)$
D
$\left(\frac{12}{7}, \infty\right)$
Solution
For angle to be acute
$ \overrightarrow{ u } \cdot \overrightarrow{ v }>0 $
$ \Rightarrow a \left(\log _{ e } b \right)^2-12+6 a \left(\log _{ e } b \right)>0$
$ \forall b >1 $
$ \text { let } \log _{ e } b = t \Rightarrow t >0 \text { as } b >1 $
$ y = at ^2+6 at -12 \& y >0, \forall t >0 $
$ \Rightarrow a \in \phi$
A
$\frac{32}{\sqrt{3}}(\sqrt{3}-1)$
B
$\frac{32}{\sqrt{3}}(2-\sqrt{3})$
C
$\frac{16}{\sqrt{3}}(\sqrt{3}-1)$
D
$\frac{16}{\sqrt{3}}(2-\sqrt{3})$
Solution

$ \frac{ OP }{ OA }=\tan 15^{\circ} $
$ \Rightarrow OA = OP \cot 15^{\circ} $
$ \frac{ OP }{ OC }=\tan 45^{\circ} \Rightarrow OP = OC$
$ \text { Now, } OP =\sqrt{ OA ^2-8^2} $
$\Rightarrow OP ^2=( OP )^2 \cot ^2 15^{\circ}-64 $
$ \Rightarrow OP ^2=\frac{32}{\sqrt{3}}(2-\sqrt{3})$
A
Both (S1) and (S2) are true
B
Both (S1) and (S2) are false
C
Only (S1) is true
D
Only (S2) is true
Solution
$P ( A \mid B )=\frac{1}{7} \Rightarrow \frac{ P ( A \cap B )}{ P ( B )}=\frac{1}{7}$
$ \Rightarrow P ( B )=\frac{7}{9}$
$P ( B \mid A )=\frac{2}{5} \Rightarrow \frac{ P ( A \cap B )}{ P ( A )}=\frac{2}{5}$
$ \Rightarrow P ( A )=\frac{5}{18} $
$\text { Now, } P \left( A ^{\prime} \cup B \right)=1- P ( A \cup B )+ P ( B )$
$ =1- P ( A )+ P ( A \cap B )=\frac{5}{6}$
$ P \left( A ^{\prime} \cap B ^{\prime}\right)=1- P ( A \cup B ) $
$ =1- P ( A )- P ( B )+ P ( A \cap B )=\frac{1}{18} $
$ \Rightarrow $ Both (S1) and (S2) are true
A
$((\sim q ) \wedge( r \vee s )) \Rightarrow p$
B
$( q \wedge( r \vee s )) \Rightarrow p$
C
$p \Rightarrow( q \wedge( r \vee s ))$
D
$p \Rightarrow((\sim q ) \wedge( r \vee s ))$
Solution
$p \equiv$ Ramesh listens to music
$\sim q \equiv He$ is in village.
$r \vee s \equiv$ Saturday or sunday
$p \Rightarrow((\sim q ) \wedge( r \vee s ))$
Answer: 57
Solution
${ }^4 C_2 \times \frac{\beta^2}{6},-6 \beta,-{ }^6 C_3 \times \frac{\beta^3}{8}$ are in A.P
$ \beta^2-\frac{5}{2} \beta^3=-12 \beta$
$ \beta=\frac{12}{5} \text { or } \beta=-2$
$ \therefore \beta=\frac{12}{5}$
$ d=-\frac{72}{5}-\frac{144}{25}=-\frac{504}{25}$
$ \therefore 50-\frac{2 d}{\beta^2}=57$
Answer: 17
Solution
$ { }^{ b } C _3 \times{ }^{ g } C _2=168 $
$ b ( b -1)( b -2)( g )( g -1)=8 \times 7 \times 6 \times 3 \times 2$
$b +3 g =17$
Answer: 13
Solution
Ellipse is
$\frac{ x ^2}{2}+\frac{ y ^2}{4}=1 ; e =\frac{1}{\sqrt{2}} ; S \equiv(0,-\sqrt{2})$
Chord of contact is
$\frac{ x }{\sqrt{2}}+\frac{(2 \sqrt{2}-2) y }{4}=1$
$ \Rightarrow \frac{ x }{\sqrt{2}}=1-\frac{(\sqrt{2}-1) y }{2} \text { solving with ellipse }$
$ \Rightarrow y =0, \sqrt{2} \therefore x =\sqrt{2}, 1$
$P \equiv(1, \sqrt{2}) Q \equiv(\sqrt{2}, 0)$
$ \therefore( SP )^2+( SQ )^2=13$
Answer: 99
Solution
$ 1+\left(1+2^{49}\right)\left(2^{49}-1\right)=2^{98} $
$ m =1, n =98 $
$ m + n =99$
Answer: 9
Solution
$ y^2=-\frac{x}{2}$
$ y=m x-\frac{1}{8 m}$
this tangent pass through $(2,0)$
$m =\pm \frac{1}{4}$
i.e., one tangent is $x-4 y-2=0$
$17 r =9$
Answer: 12
Solution
$ \frac{6}{3^{12}}+10\left(\frac{1}{3^{11}}+\frac{2}{3^{10}}+\frac{2^2}{3^9}+\frac{2^3}{3^8}+\ldots . .+\frac{2^{10}}{3}\right) $
$ \frac{6}{3^{12}}+\frac{10}{3^{11}}\left(\frac{6^{11}-1}{6-1}\right) $
$ =2^{12} \cdot 1 ; m \cdot n =12$
Answer: 5
Solution
$ \tan \theta+\sqrt{5} \tan 2 \theta \tan \theta=\sqrt{5}-\tan 2 \theta$
$ \tan 3 \theta=\sqrt{5}$
$\theta=\frac{ n \pi}{3}+\frac{\alpha}{3} ; \quad \tan \alpha=\sqrt{5}$
Five solution
Answer: 6
Solution
Sol. $\left| z ^2\right|=|\overline{ z }| \cdot 2^{1-| z |} \Rightarrow| z |=1$
$z ^2=\overline{ z } \Rightarrow z ^3=1 $
$\therefore z =\omega \text { or } \omega^2$
$\omega^{ n }=(1+\omega)^{ n }=\left(-\omega^2\right)^{ n }$
Least natural value of $n$ is 6 .
Answer: 56
Solution

$ \sigma^2=\sum X^2 P(X)-\left(\sum X P(X)\right)^2=\frac{56}{100} $
$ 100 \sigma^2=56$
Answer: 104