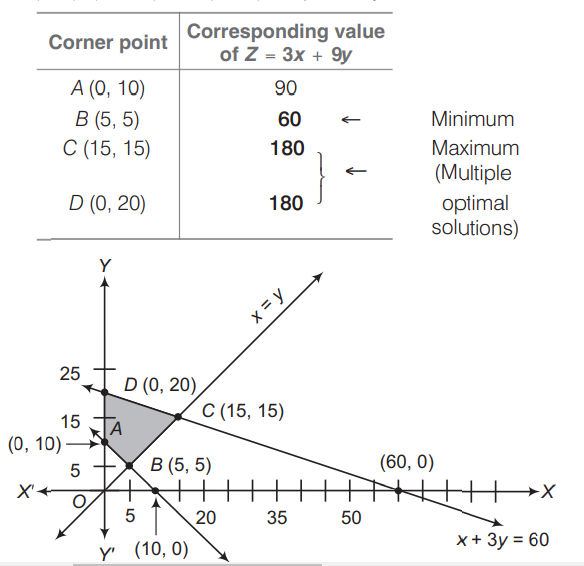
Q.
The minimum and maximum values of for the problem,
minimise and maximise ...(i)
subject to the constraints
...(ii)
...(iii)
...(iv)
...(v)
are respectively
Solution: