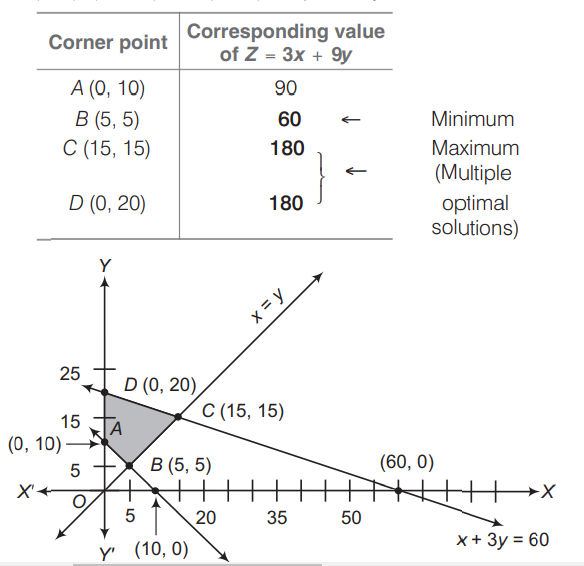
Q.
The minimum and maximum values of $Z$ for the problem,
minimise and maximise $Z=3 x+9 y$...(i)
subject to the constraints
$x+3 y \leq 60$...(ii)
$x+y \geq 10$...(iii)
$x \leq y $...(iv)
$x \geq 0, y \geq 0$...(v)
are respectively
Linear Programming
Solution: