Question

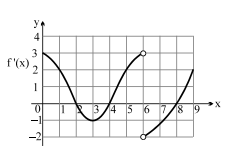
The graph of the derivative $f^{\prime }$ 'of a continuous function $f$ is shown with $f(0)=0$. If
(i) $f$ is monotomic increasing in the interval $[a,b)\cup (c,d)\cup (e,f]$ and decreasing in $(p,q)\cup (r,s)$.
(ii) $f$ has a local minima at $x=x_1$ and $x=x_2$.
(iii) $f$ is concave up in $(l,m)\cup (n,t]$
(iv) $f$ has inflection point at $x=k$
(v) number of critical points of $y=f(x)$ is ' $w$ '.
Find the value of $(a+b+c+d+e)+(p+q+r+s)+(l+m+n)+\left(x_1+x_2\right)+(k+w)$.

Answer 1

Answer: 0074

(i) increasing on $[0,2),(4,6),(8,9]$ as $f^{\prime }(x)>0$ and decreasing on $(2,4),(6,8)$ as $f^{\prime }(x)<0$
(ii) local minima at $x=4,8$
(iii) $CU$ on $(3,6),(6,9]$
(iv) $k=3$
(v) $w=4$ i.e. $(x=2,4,6$ and 8$)$
hence
$(a+b+c+d+e)+(p+q+r+s)+(l+m+n)+\left(x_1+x_2\right)+(k+w)$
$=(0+2+4+6+8)+(2+4+6+8)+(3+6+6)+(4+8)+(3+4)$
$=(20)+(20)+(15)+(12)+(7)=74$