Q.
The graph of the derivative $f^{\prime}$ 'of a continuous function $f$ is shown with $f(0)=0$. If
(i) $f$ is monotomic increasing in the interval $[ a , b ) \cup( c , d ) \cup( e , f ]$ and decreasing in $( p , q ) \cup( r , s )$.
(ii) $f$ has a local minima at $x = x _1$ and $x = x _2$.
(iii) $f$ is concave up in $(l, m ) \cup( n , t ]$
(iv) $f$ has inflection point at $x = k$
(v) number of critical points of $y=f(x)$ is ' $w$ '.
Find the value of $( a + b + c + d + e )+( p + q + r + s )+( l + m + n )+\left( x _1+ x _2\right)+( k + w )$.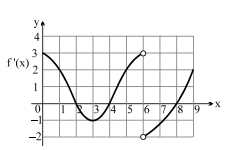
Application of Derivatives
Solution:
